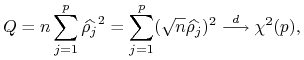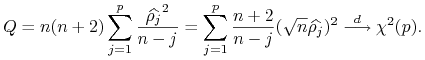11. Testowanie autokorelacji składnika losowego i składnika resztowego
Rozkład współczynników autokowariancji i autokorelacji empirycznych. Statystyki ![]() Ljunga-Boxa i Boxa-Pierce'a.
(1 wykład)
Ljunga-Boxa i Boxa-Pierce'a.
(1 wykład)
11.1. Autokorelacja składnika losowego
Niech ![]() skalarny proces stochastyczny (szereg czasowy), stacjonarny, ergodyczny i klasy
skalarny proces stochastyczny (szereg czasowy), stacjonarny, ergodyczny i klasy ![]() . Dodatkowo założymy, że zmienne losowe
. Dodatkowo założymy, że zmienne losowe ![]() nie są stałe (deterministyczne).
nie są stałe (deterministyczne).
Ze stacjonarności wynika, że kowariancja ![]() i
i ![]() zależy tylko od różnicy
zależy tylko od różnicy ![]() .
.
Definicja 11.1
![]() -tym współczynnikiem autokowariancji nazywamy kowariancję zmiennych losowych
-tym współczynnikiem autokowariancji nazywamy kowariancję zmiennych losowych ![]() odległych o
odległych o ![]()
Jak łatwo zauważyć
oraz
Definicja 11.2
![]() -tym współczynnikiem autokorelacji nazywamy współczynnik korelacji zmiennych losowych
-tym współczynnikiem autokorelacji nazywamy współczynnik korelacji zmiennych losowych ![]() odległych o
odległych o ![]()
Naszym celem jest
estymacja współczynników autokowariancji i autokorelacji na podstawie ![]() -elementowej próbki
-elementowej próbki ![]() ,
, ![]() .
Będziemy korzystali z następujących estymatorów:
.
Będziemy korzystali z następujących estymatorów:
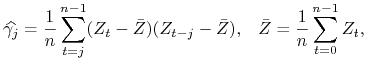 |
Uwaga 11.1
Z ergodyczności procesu ![]() wynika, że estymatory
wynika, że estymatory ![]() i
i ![]() są zgodne
są zgodne
Przy pewnych dodatkowych założeniach można pokazać, że estymatory ![]() i
i ![]() są asymptotycznie normalne.
są asymptotycznie normalne.
Twierdzenie 11.1
Niech
gdzie ![]() jest pewną stałą,
a stacjonarny i ergodyczny proces
jest pewną stałą,
a stacjonarny i ergodyczny proces ![]() jest ciągiem przyrostów martyngałowych takim, że
jest ciągiem przyrostów martyngałowych takim, że
Wówczas dla każdego ![]()
gdzie
Dowód.
Zaczniemy od wyznaczenia pierwszego i drugiego momentu ![]() oraz kowariancji
oraz kowariancji ![]() i
i ![]() dla
dla ![]()
Podsumowując
a zatem
Następnie zajmiemy się badaniem procesów iloczynów
zatem wszystkie procesy ![]() są ciągami przyrostów martyngałowych.
Wyznaczymy wariancję
są ciągami przyrostów martyngałowych.
Wyznaczymy wariancję ![]() i kowariancję
i kowariancję ![]() i
i ![]() dla
dla ![]()
Oznaczmy przez ![]() wektor o wyrazach
wektor o wyrazach ![]() dla
dla ![]() od 1 do
od 1 do ![]()
Proces ![]() jest stacjonarnym i ergodycznym ciągiem przyrostów martyngałowych o skończonej sferycznej wariancji
jest stacjonarnym i ergodycznym ciągiem przyrostów martyngałowych o skończonej sferycznej wariancji
Zatem na mocy Centralnego Twierdzenia Granicznego (Tw. 8.6)
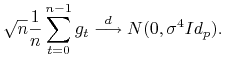 |
Zauważmy, że
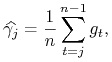 |
zatem, również
Natomiast
Ponieważ
to
W praktycznych zastosowaniach wygodniej jest stosować statystyki 1-wymiarowe.
Przykładem są statystyki ![]() :
:![]() Boxa-Pierce'a
Boxa-Pierce'a
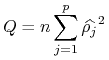 |
![]() i Ljunga-Boxa
i Ljunga-Boxa
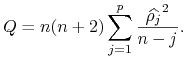 |
11.2. Autokorelacja składnika resztowego
Rozważamy model liniowy z wyrazem wolnym
spełniający warunki Z̃1 – Z̃5.
Niech ![]() będzie estymatorem MNK wyznaczonym na podstawie próbki
będzie estymatorem MNK wyznaczonym na podstawie próbki ![]() -elementowej, a
-elementowej, a ![]() składnikiem resztowym
składnikiem resztowym
Przyjmiemy następujące oznaczenia:![]() i
i ![]() współczynniki autokowariancji i autokorelacji składnika losowego
współczynniki autokowariancji i autokorelacji składnika losowego ![]()
![]() i
i ![]() współczynniki ”próbkowe” autokowariancji i autokorelacji składnika losowego
współczynniki ”próbkowe” autokowariancji i autokorelacji składnika losowego ![]()
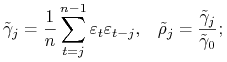 |
![]() i
i ![]() współczynniki próbkowe autokowariancji i autokorelacji składnika losowego
współczynniki próbkowe autokowariancji i autokorelacji składnika losowego ![]()
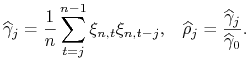 |
Proces ![]() jest stacjonarny i ergodyczny zatem dla każdego
jest stacjonarny i ergodyczny zatem dla każdego ![]()
Niestety, składnik ![]() jest nieobserwowalny. Znamy tylko składnik resztowy
jest nieobserwowalny. Znamy tylko składnik resztowy ![]() ,
zatem jako ewentualne estymatory można rozważać
,
zatem jako ewentualne estymatory można rozważać ![]() i
i ![]() .
.
Pytanie?
Czy można zastąpić w statystyce ![]() współczynniki ”próbkowe” autokorelacji składnika losowego
współczynniki ”próbkowe” autokorelacji składnika losowego ![]() , przez
współczynniki ”próbkowe” autokorelacji składnika resztowego
, przez
współczynniki ”próbkowe” autokorelacji składnika resztowego ![]() , nie psując własności tej statystyki?
, nie psując własności tej statystyki?
Okazuje się, że przy dodatkowych założeniach odpowiedź jest pozytywna.
Lemat 11.1
Dowód.
Skorzystamy z zależności
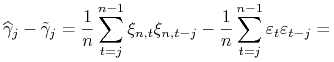 |
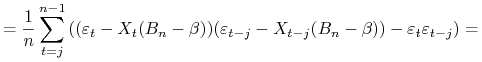 |
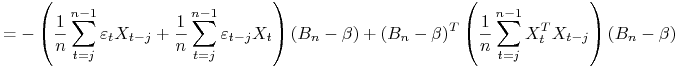 |
Natomiast dla ![]() mamy
mamy
Lemat 11.2
Jeśli dodatkowo spełniony jest warunek ścisłej egzogeniczności (Z2)
to
Dowód.
Zauważmy, że ze ścisłej egzogeniczności wynika, że
Niech ![]() będzie pewną zmienną losową o rozkładzie
będzie pewną zmienną losową o rozkładzie ![]() . Wówczas
. Wówczas
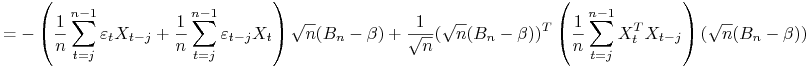 |
Zbieżność do zera według rozkładu implikuje zbieżność do 0 według prawdopodobieństwa, zatem
Dowód zbieżności dla ![]() przebiega analogicznie jak w poprzednim lemacie.
przebiega analogicznie jak w poprzednim lemacie.
Wniosek 11.2
Przy założeniach lematu 11.2
statystyka ![]() policzona dla
policzona dla ![]() jest asymptotycznie równoważna statystyce
jest asymptotycznie równoważna statystyce ![]() policzonej dla
policzonej dla ![]() , zatem obie zbiegają według rozkładu do
, zatem obie zbiegają według rozkładu do ![]() .
.