Zagadnienia

13.1 Model tendencji rozwojowej z liniowym trendem

13. Regresja względem czasu.

Teoria dużej próbki cd. Model tendencji rozwojowej z liniowym trendem. Estymatory hiper-zgodne.

13.1. Model tendencji rozwojowej z liniowym trendem

13.1.1. Założenia modelu

Rozważamy następujący model liniowy

$Y_{t}=\beta _{1}t+\beta _{2}+\varepsilon _{t},$

(13.1)

gdzie
$t$ – czas (kolejny moment), $t\in\mathbb{N}$ (lub $t\in\mathbb{Z}$ ),
$\{\varepsilon _{t}\}$ – niezależny, biały szum; tzn. $\varepsilon _{t}$ nie zależą od historii i mają ten sam rozkład. Ponadto zakładamy, że $\varepsilon\in L^{4}$ , $E(\varepsilon)=0$ oraz $E(\varepsilon _{t}^{2})=\sigma^{2}>0$ .

Przyjmiemy następujące oznaczenia

$X_{t}=(t,1),\;\;\;\beta=(\beta _{1},\beta _{2})^{T}.$

Wówczas model 13.1 można zapisać w następujący sposób

$Y_{t}=X_{t}\beta+\varepsilon _{t}.$

W zapisie macierzowym otrzymamy

$Y=X\beta+\varepsilon.$

Powyższy model spełnia założenia modelu klasycznego Z1 – Z4 (bez założenia o normalności składnika losowego) i nie spełnia założeń modelu ”dużej próbki”, bo proces $\{ t\}$ nie jest stacjonarny.

Problem.
Co można powiedzieć o asymptotyce estymatorów MNK dla modelu opisanego równaniem 13.1?

13.1.2. Estymacja parametrów modelu

Rozważmy proces generujący dane $\{ Y_{t},X_{t}\} _{{t=0}}^{\infty}$ , z którego bierzemy $n$ -elementową próbkę dla $t=0,\dots,n-1$ . MNK estymator wektora $\beta$ wyznaczamy ze wzoru

$B=(X^{T}X)^{{-1}}X^{T}Y=S_{{xx}}^{{-1}}S_{{xy}},$

gdzie

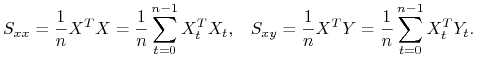$S_{{xx}}=\frac{1}{n}X^{T}X=\frac{1}{n}\sum _{{t=0}}^{{n-1}}X_{t}^{T}X_{t},\;\;\; S_{{xy}}=\frac{1}{n}X^{T}Y=\frac{1}{n}\sum _{{t=0}}^{{n-1}}X_{t}^{T}Y_{t}.$

Natomiast MNK estymator wariancji $\sigma^{2}$ wynosi

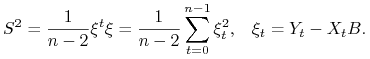$S^{2}=\frac{1}{n-2}\xi^{t}\xi=\frac{1}{n-2}\sum _{{t=0}}^{{n-1}}\xi _{t}^{2},\;\;\;\xi _{t}=Y_{t}-X_{t}B.$

Twierdzenie 13.1

$\left(\begin{array}[]{c}\sqrt{n}^{{3}}(B_{1}-\beta _{1})\\ \sqrt{n}(B_{2}-\beta _{2})\end{array}\right)\stackrel{d}{\longrightarrow}N(0,\sigma^{2}\Sigma),\;\;\;\Sigma=\left(\begin{array}[]{rr}12&-6\\ -6&4\end{array}\right).$

Dowód.
Zauważmy, że

$B-\beta=S_{{xx}}^{{-1}}\bar{g}^{T},$

gdzie

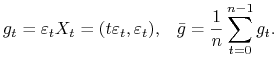$g_{t}=\varepsilon _{t}X_{t}=(t\varepsilon _{t},\varepsilon _{t}),\;\;\;\bar{g}=\frac{1}{n}\sum _{{t=0}}^{{n-1}}g_{t}.$

Macierz $S_{{xx}}$ można łatwo wyliczyć

$S_{{xx}}=\frac{1}{n}\sum _{{t=0}}^{{n-1}}X_{t}^{T}X_{t}=\frac{1}{n}\sum _{{t=0}}^{{n-1}}\left(\begin{array}[]{c}t\\ 1\end{array}\right)\circ(t,1)=$

$=\frac{1}{n}\sum _{{t=0}}^{{n-1}}\left(\begin{array}[]{cc}t^{2}&t\\ t&1\end{array}\right)=\left(\begin{array}[]{cc}\frac{(n-1)(2n-1)}{6}&\frac{n-1}{2}\\ \frac{n-1}{2}&1\end{array}\right).$

Gdy $n$ rośnie do nieskończoności to 3 wyrazy macierzy $S_{{xx}}$ zbiegają do nieskończoności

$\left(\begin{array}[]{cc}\frac{(n-1)(2n-1)}{6}&\frac{n-1}{2}\\ \frac{n-1}{2}&1\end{array}\right)\longrightarrow\left(\begin{array}[]{cc}\infty&\infty\\ \infty&1\end{array}\right).$

Aby uzyskać rodzine macierzy o skończonej granicy pomnożymy macierz $S_{{xx}}$ z obu stron przez macierz diagonalną

$\Phi _{n}=\left(\begin{array}[]{cc}n^{{-1}}&0\\ 0&1\end{array}\right).$

Otrzymujemy

$\Phi _{n}S_{{xx}}\Phi _{n}=\left(\begin{array}[]{cc}\frac{(n-1)(2n-1)}{6n^{2}}&\frac{n-1}{2n}\\ \frac{n-1}{2n}&1\end{array}\right)\longrightarrow Q,$

gdzie

$Q=\left(\begin{array}[]{cc}\frac{1}{3}&\frac{1}{2}\\ \frac{1}{2}&1\end{array}\right).$

Z drugiej strony z centralnego twierdzenia granicznego Linderberga-Levy'ego ([9] §10.2 Twierdzenie 1) otrzymujemy asymptotyczną normalność $\Phi _{n}\bar{g}$

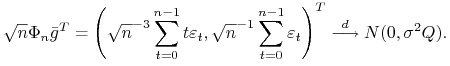$\sqrt{n}\Phi _{n}\bar{g}^{T}=\left(\sqrt{n}^{{-3}}\sum _{{t=0}}^{{n-1}}t\varepsilon _{t},\sqrt{n}^{{-1}}\sum _{{t=0}}^{{n-1}}\varepsilon _{t}\right)^{T}\stackrel{d}{\longrightarrow}N(0,\sigma^{2}Q).$

Podsumowując

$\left(\begin{array}[]{c}\sqrt{n}^{{3}}(B_{1}-\beta _{1})\\ \sqrt{n}(B_{2}-\beta _{2})\end{array}\right)=\sqrt{n}\Phi _{n}^{{-1}}(B-\beta)=\sqrt{n}\Phi _{n}^{{-1}}S_{{xx}}^{{-1}}\bar{g}^{T}=$

$=\sqrt{n}\Phi _{n}^{{-1}}S_{{xx}}^{{-1}}\Phi _{n}^{{-1}}\Phi _{n}\bar{g}^{T}=(\Phi _{n}S_{{xx}}\Phi _{n})^{{-1}})\cdot\sqrt{n}\Phi _{n}\bar{g}^{T}.$

Ponieważ macierze $(\Phi _{n}S_{{xx}}\Phi _{n})^{{-1}}$ zbiegają do $Q^{{-1}}$ , a proces $\sqrt{n}\Phi _{n}\bar{g}^{T}$ zbiega według rozkładu do $N(0,\sigma^{2}Q)$ to

$\left(\begin{array}[]{c}\sqrt{n}^{{3}}(B_{1}-\beta _{1})\\ \sqrt{n}(B_{2}-\beta _{2})\end{array}\right)\stackrel{d}{\longrightarrow}N(0,\sigma^{2}Q^{{-1}}QQ^{{-1}})=N(0,\sigma^{2}Q^{{-1}}).$

Aby zakończyć dowód wystarczy zauważyć, że

$Q^{{-1}}=\Sigma.$

$\Box$

Uwaga 13.1

Estymator $B_{1}$ nazywa się estymatorem $n^{{3/2}}$ -zgodnym albo hiper-zgodnym (hyper-consistent).

Twierdzenie 13.2

Estymator $S^{2}$ jest zgodny

$S^{2}\stackrel{p}{\longrightarrow}\sigma^{2}.$

Dowód.
Jak pokazaliśmy w rozdziale 4 (patrz równanie 4.3)

$\xi^{T}\xi=\varepsilon^{T}M\varepsilon,$

gdzie $M$ macierz rzutu na dopełnienie ortogonalne podprzestrzeni rozpiętej przez kolumny macierzy $X$

$M=Id-X(X^{T}X)^{{-1}}X^{T}.$

Zatem

$S^{2}=\frac{1}{n-2}\xi^{t}\xi=\frac{1}{n-2}(\varepsilon^{T}\varepsilon-\varepsilon^{T}X(X^{T}X)^{{-1}}X^{T}\varepsilon)=\frac{1}{n-2}(\varepsilon^{T}\varepsilon-\varepsilon^{T}X(B-\beta)).$

Stosując notację i oszacowania z dowodu poprzedniego twierdzenia otrzymujemy

$S^{2}=\frac{n}{n-2}\left(\frac{1}{n}\varepsilon^{T}\varepsilon-\bar{g}\Phi _{n}\Phi _{n}^{{-1}}(B-\beta)\right)\stackrel{p}{\longrightarrow}\sigma^{2}-0.$

$\Box$

13.1.3. Testowanie parametrów strukturalnych

Dla $k=0,1$ testujemy hipotezę

$H_{{k,0}}:\beta _{k}=\bar{\beta _{k}},$

wobec hipotezy alternatywnej

$H_{{k,1}}:\beta _{k}\neq\bar{\beta _{k}}.$

Analogicznie jak w modelu klasycznym przyjmujemy

$T_{1}=\frac{B_{1}-\bar{\beta _{1}}}{SE(B_{1})},\;\;\; T_{2}=\frac{B_{2}-\bar{\beta _{2}}}{SE(B_{2})},$

gdzie

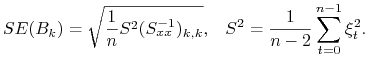$SE(B_{k})=\sqrt{\frac{1}{n}S^{2}(S_{{xx}}^{{-1}})_{{k,k}}},\;\;\; S^{2}=\frac{1}{n-2}\sum _{{t=0}}^{{n-1}}\xi _{t}^{2}.$

Twierdzenie 13.3

Przy założeniu hipotezy zerowej $H_{{k,0}}$ rozkład statystyki $T_{k}$ zbiega do N(0,1).

Dowód.
Korzystamy z faktu, że $S^{2}$ zbiega do $\sigma^{2}$ , $n^{2}(S_{{xx}}^{{-1}})_{{1,1}}$ do $\Sigma _{{1,1}}$ , a $(S_{{xx}}^{{-1}})_{{2,2}}$ do $\Sigma _{{2,2}}$ .

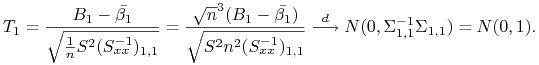$T_{1}=\frac{B_{1}-\bar{\beta _{1}}}{\sqrt{\frac{1}{n}S^{2}(S_{{xx}}^{{-1}})_{{1,1}}}}=\frac{\sqrt{n}^{3}(B_{1}-\bar{\beta _{1}})}{\sqrt{S^{2}n^{2}(S_{{xx}}^{{-1}})_{{1,1}}}}\stackrel{d}{\longrightarrow}N(0,\Sigma _{{1,1}}^{{-1}}\Sigma _{{1,1}})=N(0,1).$

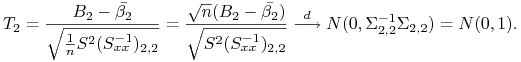$T_{2}=\frac{B_{2}-\bar{\beta _{2}}}{\sqrt{\frac{1}{n}S^{2}(S_{{xx}}^{{-1}})_{{2,2}}}}=\frac{\sqrt{n}(B_{2}-\bar{\beta _{2}})}{\sqrt{S^{2}(S_{{xx}}^{{-1}})_{{2,2}}}}\stackrel{d}{\longrightarrow}N(0,\Sigma _{{2,2}}^{{-1}}\Sigma _{{2,2}})=N(0,1).$

$\Box$

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Ekonometria

Zagadnienia

13. Regresja względem czasu.

13.1. Model tendencji rozwojowej z liniowym trendem

13.1.1. Założenia modelu

13.1.2. Estymacja parametrów modelu

Twierdzenie 13.1

Uwaga 13.1

Twierdzenie 13.2

13.1.3. Testowanie parametrów strukturalnych

Twierdzenie 13.3