Zagadnienia
4. Klasyczny model regresji
Klasyczny jednorównaniowy liniowy model ekonometryczny. Założenia modelu. Estymacja parametrów strukturalnych modelu metodą najmniejszych kwadratów (regresja wieloraka). (1 wykład)
4.1. Notacja macierzowa dla zmiennych losowych
Definicja 4.1
Niech ![]() będzie
będzie ![]() macierzą losową, której wyrazami są zmienne losowe
macierzą losową, której wyrazami są zmienne losowe ![]() określone na tej samej przestrzeni probabilistycznej.
Wartością oczekiwaną
określone na tej samej przestrzeni probabilistycznej.
Wartością oczekiwaną ![]() będziemy nazywać
będziemy nazywać ![]() macierz
macierz ![]() taką, że
taką, że
Uwaga 4.1
Wartość oczekiwana macierzy jest zgodna z transpozycją
oraz z mnożeniem przez macierze deterministyczne
gdzie ![]() i
i ![]() macierze o współczynnikach rzeczywistych odpowiednio wymiaru
macierze o współczynnikach rzeczywistych odpowiednio wymiaru ![]() i
i ![]() .
.
Definicja 4.2
Niech ![]() będzie
będzie ![]() macierzą losową (wektorem kolumnowym), której wyrazami są zmienne losowe
macierzą losową (wektorem kolumnowym), której wyrazami są zmienne losowe ![]() określone na tej samej przestrzeni probabilistycznej.
Macierzą kowariancji
określone na tej samej przestrzeni probabilistycznej.
Macierzą kowariancji ![]() będziemy nazywać
będziemy nazywać ![]() macierz
macierz ![]()
Uwaga 4.2
Zachodzą następujące związki
![]() jest macierzą symetryczną
jest macierzą symetryczną
Ponadto dla deterministycznej ![]() macierzy
macierzy ![]()
Definicja 4.3
Niech ![]() i
i ![]() będą wektorami kolumnowymi, których wyrazami są zmienne losowe
będą wektorami kolumnowymi, których wyrazami są zmienne losowe ![]() ,
, ![]() i
i ![]() ,
,
![]() określone na tej samej przestrzeni probabilistycznej.
Macierzą kowariancji
określone na tej samej przestrzeni probabilistycznej.
Macierzą kowariancji ![]() i
i ![]() będziemy nazywać
będziemy nazywać ![]() macierz
macierz ![]()
Uwaga 4.3
Zachodzą następujące związki
Ponadto dla deterministycznych ![]() macierzy
macierzy ![]() i
i ![]()
![]()
4.2. Warunkowa wartość oczekiwana
Niech ![]() będzie przestrzenią probabilistyczną,
będzie przestrzenią probabilistyczną, ![]()
![]() -ciałem zawartym w
-ciałem zawartym w ![]() a
a ![]() zmienną losową określoną na
zmienną losową określoną na ![]() .
.
Definicja 4.4
Warunkową wartością oczekiwaną ![]() pod warunkiem
pod warunkiem ![]() nazywamy każdą zmienną losową
nazywamy każdą zmienną losową
![]() o wartościach w
o wartościach w ![]() spełniającą warunki:
spełniającą warunki:
i) ![]() jest
jest ![]() mierzalna;
mierzalna;
ii) Dla każdego ![]()
Lemat 4.1
Każdy z poniższych warunków implikuje istnienie warunkowej wartości oczekiwanej
![]() .
.
1. ![]() jest określona (tzn. skończona lub nieskończona).
jest określona (tzn. skończona lub nieskończona).
2. ![]() należy do
należy do ![]() .
.
3. ![]() p.n. lub
p.n. lub ![]() p.n.
p.n.
Uwaga 4.4
Warunkowa wartość oczekiwana ma następujące własności:
1. ![]() p.n. to
p.n. to ![]() p.n.
p.n.
2. ![]() p.n.
p.n.
3. ![]() o ile prawa strona jest określona (tzn. różna od
o ile prawa strona jest określona (tzn. różna od ![]() ),
),
4. Jeżeli zmienna losowa ![]() jest
jest ![]() mierzalna i wartość oczekiwana
mierzalna i wartość oczekiwana ![]() jest określona to
jest określona to
5. Jeżeli wartość oczekiwana ![]() jest określona to dla dowolnego
jest określona to dla dowolnego ![]() -ciała
-ciała ![]() zawartego w
zawartego w ![]()
W szczególności
4.3. Założenia klasycznego modelu regresji
W modelu regresji rozważa się zmienną objaśnianą (zależną, zwaną też regressandem) - ![]() i zmienne objaśniające (zwane regressorami) -
i zmienne objaśniające (zwane regressorami) - ![]() .
.
Dysponujemy próbką złożoną z ![]() obserwacji.
obserwacji. ![]() -tą obserwację modelujemy jako realizację
-tą obserwację modelujemy jako realizację
![]() wymiarowej zmiennej losowej
wymiarowej zmiennej losowej
Przez model rozumie się łączny rozkład zmiennych losowych ![]() i
i ![]() spełniający pewne założenia.
spełniający pewne założenia.
Założenia modelu.
Z1. Liniowość.
Zmienne losowe ![]() i
i ![]() należą do
należą do ![]() i spełniają zależność
i spełniają zależność
gdzie ![]() to deterministyczne choć na ogół nieznane parametry regresji zwane też parametrami strukturalnymi modelu, zaś zmienne losowe
to deterministyczne choć na ogół nieznane parametry regresji zwane też parametrami strukturalnymi modelu, zaś zmienne losowe ![]() to składniki losowe.
Funkcję
to składniki losowe.
Funkcję
nazywa się funkcją regresji. Warunek liniowości można zapisać w postaci macierzowej
gdzie ![]() macierz o wyrazach
macierz o wyrazach ![]() ,
, ![]() ,
, ![]() i
i ![]() wektory kolumnowe o wyrazach odpowiednio
wektory kolumnowe o wyrazach odpowiednio
![]() ,
, ![]() i
i ![]() .
.
Uwaga 4.5
Założenie Z1 implikuje przynależność ![]() do
do ![]() .
.
Z2. Ścisła egzogeniczność.
Wniosek 4.1
Przy założeniach Z1 i Z2 dla wszystkich ![]() i
i ![]() zachodzą
następujące równości:
zachodzą
następujące równości:
1. ![]() ;
;
2. ![]() ;
;
3. ![]() .
.
Dowód.
Ponieważ zarówno ![]() jak i
jak i ![]() należą do
należą do ![]() (to wynika z Z1) to możemy stosować twierdzenie o iterowanej wartości oczekiwanej.
(to wynika z Z1) to możemy stosować twierdzenie o iterowanej wartości oczekiwanej.
| Ad1. | ||||
| Ad2. | ||||
| Ad3. |
Z3. Liniowa niezależność.
Warunek Z3 oznacza, że kolumny macierzy ![]() są prawie na pewno liniowo niezależne.
są prawie na pewno liniowo niezależne.
Z4. Sferyczność błędu
gdzie ![]() deterministyczny parametr modelu.
deterministyczny parametr modelu.
Warunek Z4 można rozłożyć na dwa warunki:
Z4.1. Homoskedastyczność
Z4.2. Brak korelacji, dla ![]()
Wniosek 4.2
Przy założeniach Z1, Z2 i Z4 dla wszystkich ![]() ,
, ![]() zachodzą
następujące równości:
zachodzą
następujące równości:
1. ![]() ;
;
2. ![]() .
.
Z5. Gaussowskość.
Łączny rozkład warunkowy ![]() względem
względem ![]() jest normalny.
jest normalny.
Wniosek 4.3
Przy założeniach Z1, Z2, Z4 i Z5:
1. ![]() ;
;
2. ![]() .
.
Dowód.
Punkt 1 wynika z założeń Z2 i Z5.
Punkt 2 wynika z faktu, że parametry warunkowego rozkładu ![]() nie zależy od
nie zależy od ![]() . Rzeczywiście, niech
. Rzeczywiście, niech ![]() będzie dystrybuantą rozkładu
będzie dystrybuantą rozkładu ![]() , wówczas
, wówczas
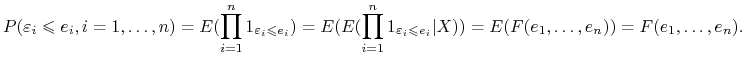 |
4.4. Estymacja parametrów modelu metodą MNK
Estymatorem MNK wektora ![]() jest wektor
jest wektor
Natomiast estmatorem MNK wariancji ![]() jest
jest
gdzie ![]() .
.
Twierdzenie 4.1
Własności estymatorów ![]() i
i ![]() :
:
a) nieobciążoność ![]() . Jeśli zachodzą Z1,Z2 i Z3 to
. Jeśli zachodzą Z1,Z2 i Z3 to
b) skończona wariancja ![]() . Jeśli zachodzą Z1,Z2,Z3 i Z4 to
. Jeśli zachodzą Z1,Z2,Z3 i Z4 to
c) efektywność (tw. Gaussa-Markowa). Jeśli zachodzą Z1,Z2,Z3 i Z4 to
estymator MNK jest najefektywniejszy w klasie liniowych po ![]() , nieobciążonych estymatorów liniowych modeli.
, nieobciążonych estymatorów liniowych modeli.
d) nieobciążoność ![]() . Jeśli zachodzą Z1,Z2,Z3 i Z4 to
. Jeśli zachodzą Z1,Z2,Z3 i Z4 to
e) ortogonalność ![]() do składnika resztowego
do składnika resztowego ![]() . Jeśli zachodzą Z1,Z2,Z3 i Z4 to
. Jeśli zachodzą Z1,Z2,Z3 i Z4 to
Dowód.
Ad.a. Najpierw pokażemy, że warunki Z3 i Z1 implikują przynależność ![]() do
do ![]() . Mamy
. Mamy
Zatem wszystkie wyrazy macierzy ![]() należą do
należą do ![]() .
Ponieważ również
.
Ponieważ również ![]() , to
, to ![]() należy do
należy do ![]() .
.
Następnie pokażemy, że ![]() .
.
Mamy dwa równania opisujące zależność ![]() od
od ![]() :
:
Po odjęciu stronami otrzymujemy:
| (4.1) |
Mnożymy obie strony przez ![]()
Biorąc pod uwagę, że ![]() (patrz wniosek 2.1) otrzymujemy:
(patrz wniosek 2.1) otrzymujemy:
| (4.2) |
Zatem
Ad.b. Pokażemy, że dla każdego wektora kolumnowego ![]()
![]() .
Skorzystamy z faktu, że wartości oczekiwane nieujemnych zmiennych losowych są zawsze określone.
.
Skorzystamy z faktu, że wartości oczekiwane nieujemnych zmiennych losowych są zawsze określone.
Założenie, że ![]() (Z3) implikuje skończoność wariancji
(Z3) implikuje skończoność wariancji ![]() dla każdego
dla każdego ![]() , a więc i wariancji
, a więc i wariancji ![]() .
.
Ad.c. Niech ![]() będzie dowolnym nieobciążonym i liniowym po
będzie dowolnym nieobciążonym i liniowym po ![]() estymatorem dla modeli liniowych z
estymatorem dla modeli liniowych z ![]() parametrami strukturalnymi i
parametrami strukturalnymi i ![]() obserwacjami. Wówczas istnieje funkcja macierzowa
obserwacjami. Wówczas istnieje funkcja macierzowa ![]() (
(![]() ), taka, że
), taka, że
Niech ![]() .
.
Ponieważ oba estymatory ![]() i
i ![]() są nieobciążone to
są nieobciążone to
Czyli dla dowolnego wektora ![]()
![]() , a zatem
, a zatem ![]() . W efekcie otrzymujemy:
. W efekcie otrzymujemy:
Teraz możemy wyznaczyc warunkową wariancje ![]() .
.
Ponieważ ![]() a
a ![]() , to
, to
Ad.d. Z równań 4.1 i 4.2 otrzymujemy, że
Jak pokazaliśmy w lemacie 2.2 macierz ![]() jest symetryczna i idempotentna, zatem
jest symetryczna i idempotentna, zatem
| (4.3) |
Ponieważ, ![]() to suma kwadratów
to suma kwadratów ![]() to jej wartości oczekiwane są zawsze określone. Otrzymujemy na mocy warunku Z3 i lematu 2.2
to jej wartości oczekiwane są zawsze określone. Otrzymujemy na mocy warunku Z3 i lematu 2.2
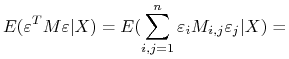 |
||||
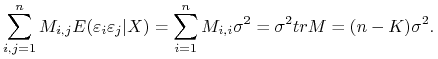 |
Ponadto
Zatem ![]() należy do
należy do ![]() .
.
Wniosek 4.4
”Bezwarunkowe” własności estymatora MNK ![]() .
.
a. Warunki Z1,Z2 i Z4 implikują, że ![]() .
.
b. Warunki Z1,Z2,Z3 i Z4 implikują, że ![]() .
.
Dowód.
Wniosek 4.5
Estymacja warunkowej kowariancji estymatora ![]() .
.
1. ![]() jest naturalnym nieobciążonym estymatorem
jest naturalnym nieobciążonym estymatorem ![]() .
.
2. ![]() jest naturalnym nieobciążonym estymatorem
jest naturalnym nieobciążonym estymatorem ![]() .
.
Dowód.
Pokażemy, że dla każdego wektora kolumnowego ![]()
![]() .
Skorzystamy z faktu, że wartości oczekiwane nieujemnych zmiennych losowych są zawsze określone.
.
Skorzystamy z faktu, że wartości oczekiwane nieujemnych zmiennych losowych są zawsze określone.
Oznaczenie.
Uwaga 4.6
Związek wariancji estymatora ![]() z wielkością próby.
z wielkością próby.
Załóżmy, że poszczególne wiersze macierzy ![]() (czyli obserwacje) są niezależne od siebie i o tym samym rozkładzie co pewien horyzontalny wektor losowy
(czyli obserwacje) są niezależne od siebie i o tym samym rozkładzie co pewien horyzontalny wektor losowy ![]() .
Wówczas z prawa wielkich liczb otrzymujemy, że istnieje pewna macierz
.
Wówczas z prawa wielkich liczb otrzymujemy, że istnieje pewna macierz ![]() taka, że
taka, że
Warunek Z3 implikuje, że macierz ![]() jest odwracalna.
Zatem
jest odwracalna.
Zatem
W efekcie




