5. Klasyczny model regresji z gaussowskim składnikiem losowym
Klasyczny jednorównaniowy liniowy model ekonometryczny -cd. Statystyczna weryfikacja modelu. (1 wykład)
Na tym wykładzie zajmiemy się ”kompletnym” modelem regresji, tzn. przyjmiemy wszystkie pięć założeń Z1 – Z5.
Lemat 5.1
Jeśli zachodzą Z1,Z2,Z3,Z4 i Z5 to estymator NMK ![]() ma warunkowy rozkład normalny
ma warunkowy rozkład normalny
Dowód.
Zatem ![]() ma rozkład normalny o wartości oczekiwanej 0 i wariancji
ma rozkład normalny o wartości oczekiwanej 0 i wariancji
5.1. Testowanie pojedynczego parametru strukturalnego 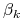
Niech ![]() pewna ustalona liczba rzeczywista.
pewna ustalona liczba rzeczywista.
Testujemy hipotezę ![]() wobec hipotezy alternatywnej
wobec hipotezy alternatywnej ![]() .
.
Twierdzenie 5.1
Przy założeniach Z1–Z5 i ![]() statystyka
statystyka ![]()
ma rozkład ![]() -Studenta z
-Studenta z ![]() stopniami swobody.
stopniami swobody.
Uwaga 5.1
Rozkład ![]() nie zależy od
nie zależy od ![]() .
.
Dowód.
zatem
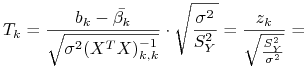 |
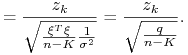 |
gdzie
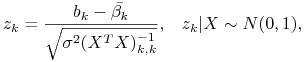 |
Lemat 5.2
Przy założeniach twierdzenia 5.1:
1. ![]() .
.
2. ![]() i
i ![]() są warunkowo względem
są warunkowo względem ![]() niezależne.
niezależne.
Dowód.
Ad.1.
zatem
zaś po odpowiednim obrocie układu współrzędnych ![]() jest macierzą diagonalną mającą na przekątnej
jest macierzą diagonalną mającą na przekątnej ![]() jedynek i
jedynek i ![]() zer, zatem
zer, zatem
Ad.2.
zatem warunkowy względem ![]() rozkład
rozkład ![]() i
i ![]() jest normalny. Ale są one warunkowo nieskorelowane a zatem warunkowo niezależne.
Ponieważ
jest normalny. Ale są one warunkowo nieskorelowane a zatem warunkowo niezależne.
Ponieważ ![]() zależy od
zależy od ![]() i
i ![]() a
a ![]() od
od ![]() i
i ![]() to są one warunkowo względem
to są one warunkowo względem ![]() niezależne.
niezależne.
Cd. dowodu twierdzenia.
Z lematu wynika, że
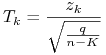 |
ma warunkowy względem ![]() rozkład t-Studenta z
rozkład t-Studenta z ![]() stopniami swobody.
Ponieważ rozkład warunkowy nie zależy od warunkowania to
stopniami swobody.
Ponieważ rozkład warunkowy nie zależy od warunkowania to ![]() ma ”bezwarunkowy” rozkład t-Studenta z
ma ”bezwarunkowy” rozkład t-Studenta z ![]() stopniami swobody.
stopniami swobody.
Reguła decyzyjna testu ![]() .
.
Przedstawimy trzy równoważne warianty reguły decyzyjnej dla zadanego poziomu istotności ![]() .
.
Wariant 1.
1. Na podstawie próbki ![]() wyznaczamy realizację statystyki testowej
wyznaczamy realizację statystyki testowej ![]() .
.
2. Wyznaczamy wartość krytyczną ![]()
3. Jeżeli ![]() to nie ma podstaw do odrzucenia hipotezy
to nie ma podstaw do odrzucenia hipotezy ![]() (akceptujemy
(akceptujemy ![]() ).
).
Jeżeli ![]() to odrzucamy
to odrzucamy ![]() na rzecz
na rzecz ![]() .
.
Wariant 2.
1. Na podstawie próbki wyznaczamy etymator ![]() i jego błąd
i jego błąd ![]() .
.
2. Wyznaczamy przedział ufności ![]()
3. Jeżeli ![]() to nie ma podstaw do odrzucenia hipotezy
to nie ma podstaw do odrzucenia hipotezy ![]() (akceptujemy
(akceptujemy ![]() ).
).
Jeżeli ![]() to odrzucamy
to odrzucamy ![]() na rzecz
na rzecz ![]() .
.
Wariant 3.
1. Na podstawie próbki ![]() wyznaczamy realizację statystyki testowej
wyznaczamy realizację statystyki testowej ![]() .
.
2. Wyznaczamy prawdopodobieństwo (tzw. ![]() -value)
-value)
3. Jeżeli ![]() to nie ma podstaw do odrzucenia hipotezy
to nie ma podstaw do odrzucenia hipotezy ![]() (akceptujemy
(akceptujemy ![]() ).
).
Jeżeli ![]() to odrzucamy
to odrzucamy ![]() na rzecz
na rzecz ![]() .
.
Uwaga 5.2
Najczęściej testujemy przypadek ![]() . Wówczas przyjecie
. Wówczas przyjecie ![]() oznacza, że zmienną objaśniającą
oznacza, że zmienną objaśniającą ![]() należy wykluczyć z naszago modelu. Tzn. jeżeli
należy wykluczyć z naszago modelu. Tzn. jeżeli
to parametr ![]() nie jest statystycznie istotny.
nie jest statystycznie istotny.
5.2. Testowanie hipotezy liniowości
Zajmiemy sie teraz testowaniem hipotezy, że nieznany parametr ![]() spełnia
spełnia ![]() niezależnych warunków liniowych.
Czyli, że należy do podprzestrzeni afinicznej kowymiaru
niezależnych warunków liniowych.
Czyli, że należy do podprzestrzeni afinicznej kowymiaru ![]() .
.
Niech ![]() macierz o współczynnikach rzeczywistych wymiaru
macierz o współczynnikach rzeczywistych wymiaru ![]() , rzędu
, rzędu ![]() , gdzie
, gdzie ![]() ,
a
,
a ![]() wektor kolumnowy wymiaru
wektor kolumnowy wymiaru ![]() .
Testujemy hipotezę
.
Testujemy hipotezę
wobec
Twierdzenie 5.2
Przy założeniach Z1–Z5 i ![]() statystka
statystka
ma rozklad F-Snedecora ![]() (rozkład
(rozkład ![]() z
z ![]() i
i ![]() stopniami swobody).
stopniami swobody).
Uwaga 5.3
Jeśli ![]() i
i ![]() są niezależnymi zmiennymi losowymi o rozkładzie
są niezależnymi zmiennymi losowymi o rozkładzie ![]() o odpowiednio
o odpowiednio ![]() i
i ![]() stopniach swobody to zmienna losowa
stopniach swobody to zmienna losowa
ma rozkład ![]() ([12] s.44-46).
([12] s.44-46).
Dowód twierdzenia.
Dzielimy licznik i mianownik przez ![]() i podstawiamy
i podstawiamy ![]() . Otrzymujemy
. Otrzymujemy
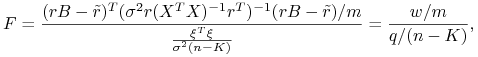 |
gdzie
Jak pokazaliśmy w lemacie 5.2 ![]() .
.
Lemat 5.3
Przy założeniach twierdzenia 5.2:
1. ![]() .
.
2. ![]() i
i ![]() są warunkowo względem
są warunkowo względem ![]() niezależne.
niezależne.
Dowód.
Ad.1.
Przyjmijmy oznaczenie ![]() .
Z
.
Z ![]() wynika, że
wynika, że ![]() , zatem
, zatem
Ponieważ warunkowy rozkład ![]() względem
względem ![]() jest normalny (lemat 5.1)to
jest normalny (lemat 5.1)to
Rzeczywiście
A więc
![]() i
i ![]() są warunkowo względem
są warunkowo względem ![]() niezależne.
Ponieważ
niezależne.
Ponieważ ![]() zależy od
zależy od ![]() i
i ![]() a
a ![]() od
od ![]() i
i ![]() to również one są warunkowo względem
to również one są warunkowo względem ![]() niezależne.
niezależne.
Cd. dowodu twierdzenia.
Z lematu wynika, że statystyka ![]() ma warunkowy względem
ma warunkowy względem ![]() rozkład F-Snedecora
rozkład F-Snedecora ![]() .
Ponieważ rozkład warunkowy nie zależy od warunkowania to
.
Ponieważ rozkład warunkowy nie zależy od warunkowania to ![]() ma ”bezwarunkowy” rozkład
ma ”bezwarunkowy” rozkład ![]() .
.
Reguła decyzyjna testu ![]() .
.
Przedstawimy dwa równoważne warianty reguły decyzyjnej dla zadanego poziomu istotności ![]() .
.
Wariant 1.
1. Na podstawie próbki ![]() wyznaczamy realizację statystyki testowej
wyznaczamy realizację statystyki testowej ![]() .
.
2. Wyznaczamy wartość krytyczną ![]()
3. Jeżeli ![]() to nie ma podstaw do odrzucenia hipotezy
to nie ma podstaw do odrzucenia hipotezy ![]() (akceptujemy
(akceptujemy ![]() ).
).
Jeżeli ![]() to odrzucamy
to odrzucamy ![]() na rzecz
na rzecz ![]() .
.
Wariant 2.
1. Na podstawie próbki ![]() wyznaczamy realizację statystyki testowej
wyznaczamy realizację statystyki testowej ![]() .
.
2. Wyznaczamy prawdopodobieństwo (tzw. ![]() -value)
-value)
3. Jeżeli ![]() to nie ma podstaw do odrzucenia hipotezy
to nie ma podstaw do odrzucenia hipotezy ![]() (akceptujemy
(akceptujemy ![]() ).
).
Jeżeli ![]() to odrzucamy
to odrzucamy ![]() na rzecz
na rzecz ![]() .
.
Statystyka ![]() w terminach sumy kwadratów reszt.
w terminach sumy kwadratów reszt.
Statystykę ![]() mozna wyrazić w prostszy sposób wykorzystując sumę kwadratów reszt modelu ograniczonego
mozna wyrazić w prostszy sposób wykorzystując sumę kwadratów reszt modelu ograniczonego
Dowód.
Krok 1. Pokażemy, że estymator OMNK (metody najmniejszych kwadratów z ograniczeniami) wynosi
Rozważamy funkcję Lagrange'a
gdzie ![]() jest
jest ![]() -elementowym wektorem wierszowym.
-elementowym wektorem wierszowym.
Różniczkujemy ![]() po współrzędnych
po współrzędnych ![]() .
.
gdzie ![]()
![]() -elementowym wektorem kolumnowym o współrzędnych 0 i 1
-elementowym wektorem kolumnowym o współrzędnych 0 i 1
Ponieważ wszystkie pochodne cząstkowe zerują się w punktach, w których funkcja przyjmuje minimum to
Czyli po transpozycji mamy
Po przemnożeniu przez macierz ![]() otrzymujemy
otrzymujemy
Ponieważ rząd ![]() macierzy
macierzy ![]() wynosi
wynosi ![]() , a macierz
, a macierz ![]() jest prawie na pewno dodatnio określona, to macierz
jest prawie na pewno dodatnio określona, to macierz ![]() jest prawie na pewno odwracalna.
Zatem
jest prawie na pewno odwracalna.
Zatem
Czyli
Krok 3.
Ponieważ ![]() , a
, a ![]() to otrzymujemy
to otrzymujemy
Sprowadzanie modelu ograniczonego do modelu z mniejszą liczbą parametrów.
Rozwiązanie ogólne układu równań liniowych ![]() mozna zapisać w postaci
parametrycznej:
mozna zapisać w postaci
parametrycznej:
gdzie ![]() jest wektorem kolumnowym
jest wektorem kolumnowym ![]() ,
, ![]() jest macierzą
jest macierzą ![]() ,
a
,
a ![]() wektor kolumnowy
wektor kolumnowy ![]() jest wektorem nieznanych parametrów, które należy wyestymować.
Zauważmy, że
jest wektorem nieznanych parametrów, które należy wyestymować.
Zauważmy, że
Model z ograniczeniami można zapisać w następujący sposób:
Po podstawieniu ![]() i
i ![]() otrzymujemy równoważny mu model zredukowany
otrzymujemy równoważny mu model zredukowany
Niech ![]() będzie estymatorem MNK
będzie estymatorem MNK ![]() dla modelu zredukowanego.
Wówczas
dla modelu zredukowanego.
Wówczas ![]() jest estymatorem
jest estymatorem ![]() dla modelu z ograniczeniami.
Zauważmy, że w obu wypadkach mamy ten sam składnik resztowy
dla modelu z ograniczeniami.
Zauważmy, że w obu wypadkach mamy ten sam składnik resztowy ![]() .
.
Test istotności regresji dla regresji z wyrazem wolnym.
W przypadku gdy ostatni parametr jest wyrazem wolnym, czyli gdy ![]() ,
stosuje się często następujący wariant testu liniowości:
,
stosuje się często następujący wariant testu liniowości:
W tym przypadku ![]() jest
jest ![]() wymiarową macierzą o wyrazach
wymiarową macierzą o wyrazach
a ![]() .
.
Statystyka ![]() wynosi wtedy
wynosi wtedy
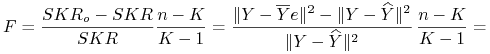 |
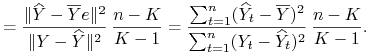 |
Uwaga 5.4
![]() można wyrazić za pomocą współczynnika determinacji
można wyrazić za pomocą współczynnika determinacji ![]()
Dowód.
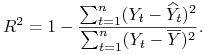 |
Dlatego też
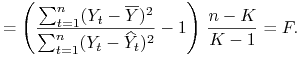 |




