Zagadnienia
7. Modele nieliniowe
Zastosowanie metody najmniejszych kwadratów w modelach nieliniowych. Opis metody. Przykłady: Modelowanie popytu konsumpcyjnego - funkcje Tórnquista. (1 wykład)
7.1. Zadanie aproksymacyjne
Dane jest ![]()
![]() -elementowych ciągów
-elementowych ciągów
oraz dana jest rodzina funkcji
![]() ,
, ![]() .
.
Zadanie:
Wyznaczyć współczynniki ![]() ,
, ![]() ,
które minimalizują błąd przybliżenia
,
które minimalizują błąd przybliżenia ![]() przez
przez ![]()
Czyli należy rozwiązać zadanie optymalizacyjne:
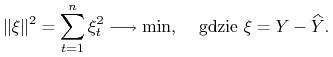 |
W ogólnym przypadku, gdy nie znamy własności funkcji ![]() , to nie wiemy czy powyższe zadanie posiada rozwiązanie i czy jeśli posiada rozwiązanie to jest ono jedynym rozwiązaniem. Gdy
, to nie wiemy czy powyższe zadanie posiada rozwiązanie i czy jeśli posiada rozwiązanie to jest ono jedynym rozwiązaniem. Gdy ![]() jest różniczkowalne to można sformułować warunki konieczne, takie jak na przykład poniższy.
jest różniczkowalne to można sformułować warunki konieczne, takie jak na przykład poniższy.
Lemat 7.1
Jeżeli ![]() jest różniczkowalne ze względu na
jest różniczkowalne ze względu na ![]() i
i ![]() należący do wnętrza zbioru
należący do wnętrza zbioru ![]() minimalizuje
minimalizuje
![]() to
wektor reszt
to
wektor reszt ![]() jest ortogonalny do wektora pochodnych
jest ortogonalny do wektora pochodnych
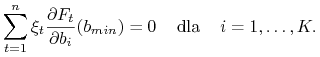 |
Dowód.
Przy założeniach lematu
suma kwadratów reszt ![]() jest różniczkowalna. Zatem w punkcie, w którym przyjmuje najmniejszą wartość jej pochodne cząstkowe muszą się zerować.
Biorąc pod uwagę, że
jest różniczkowalna. Zatem w punkcie, w którym przyjmuje najmniejszą wartość jej pochodne cząstkowe muszą się zerować.
Biorąc pod uwagę, że ![]() otrzymujemy dla każdego
otrzymujemy dla każdego ![]()
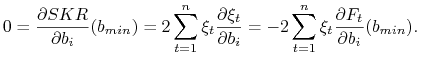 |
7.2. Założenia modelu i estymacja parametrów
Przyjmijmy dla modelu nieliniowego założenia wzorowane na modelu liniowym.
NZ1. Liniowa zależność od czynnika losowego
gdzie ![]() wektor parametrów, a
wektor parametrów, a ![]() funkcja różniczkowalna po
funkcja różniczkowalna po ![]() .
.
NZ2. Ścisła egzogeniczność.
NZ3. Liniowa niezależność pochodnych.
gdzie ![]() oznacza macierz
oznacza macierz ![]() pochodnych cząstkowych wektora
pochodnych cząstkowych wektora ![]() ,
, ![]() ,
,
NZ4. Sferyczność błędu
gdzie ![]() deterministyczny parametr modelu.
deterministyczny parametr modelu.
Naturalne jest aby
estymatorem NMNK wektora ![]() nazywać rozwiązanie zadania aproksymacyjnego z poprzedniego podrozdziału.
nazywać rozwiązanie zadania aproksymacyjnego z poprzedniego podrozdziału.
Definicja 7.1
![]() -wymiarowa zmienna losowa
-wymiarowa zmienna losowa ![]() jest estymatorem NMNK wektora
jest estymatorem NMNK wektora ![]() , gdy
, gdy
![]() przyjmuje wartości w
przyjmuje wartości w ![]() i
prawie na pewno
i
prawie na pewno
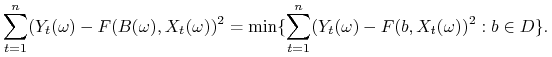 |
Lemat 7.2
Niech ![]() będzie podzbiorem otwartym
będzie podzbiorem otwartym ![]() .
Jeśli
.
Jeśli ![]() jest estymatorem NMNK wektora
jest estymatorem NMNK wektora ![]() to
to
gdzie ![]() wektor reszt rozwinięcia Taylora
wektor reszt rozwinięcia Taylora ![]() w
w ![]()
Dowód.
Mamy dwie równości wynikające z NZ1 i definicji składnika resztowego ![]()
Zatem
Czyli
Z NZ3 wynika, że macierz ![]() jest prawie na pewno odwracalna, zatem
macierz
jest prawie na pewno odwracalna, zatem
macierz ![]()
jest dobrze zdefiniowana poza, być może, zbiorem ![]() -miary zero.
-miary zero.
Zauważmy, że z definicji ![]() otrzymujemy
otrzymujemy
a z lematu 7.1
Zatem
Uwaga 7.1
Jak widać z powyższego warunek ścisłej egzogeniczności (NZ2) nie implikuje nieobciążoności estymatora NMNK.
7.3. Przykłady
Opisane w poprzednich podrozdziałach trudności związane ze stosowaniem nieliniowej metody najmniejszych kwadratów powodują, że nieliniowe modele stosuje się tylko wtedy gdy dobrze opisują fakty stylizowane związane z modelowanym zjawiskiem. Tak jak na przykład funkcje Törnquista, których przebieg ilustruje hipotezy dotyczące reakcji konsumentów na zmiany dochodów, albo funkcja logistyczna, która znalazła zastosowanie w modelowaniu długookresowego wzrostu liczby ludności i w reprezentacji rozwoju sprzedaży nowych produktów na określonym rynku.
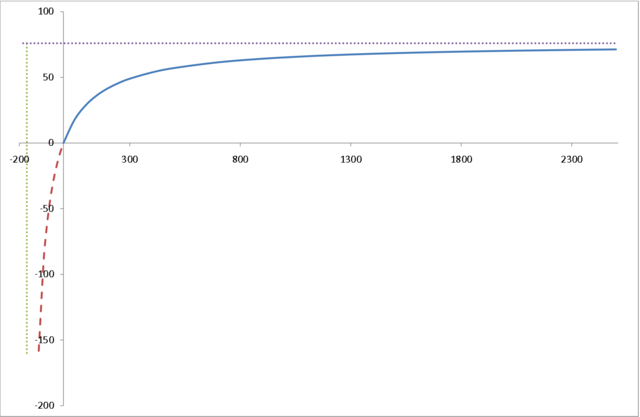
7.3.1. Funkcja Törnquista I typu
Funkcja Törnquista I typu wyraża zależność między popytem na dobra podstawowe (![]() ), a dochodami konsumentów (
), a dochodami konsumentów (![]() )
)
Popyt rośnie wraz ze wzrostem dochodów i stabilizuje się na poziomie równym ![]() .
Wykres ma asymptotę poziomą.
Z drugiej strony popyt spada do zera wraz ze spadkiem dochodów ale nie znika dla niezerowych dochodów.
.
Wykres ma asymptotę poziomą.
Z drugiej strony popyt spada do zera wraz ze spadkiem dochodów ale nie znika dla niezerowych dochodów.
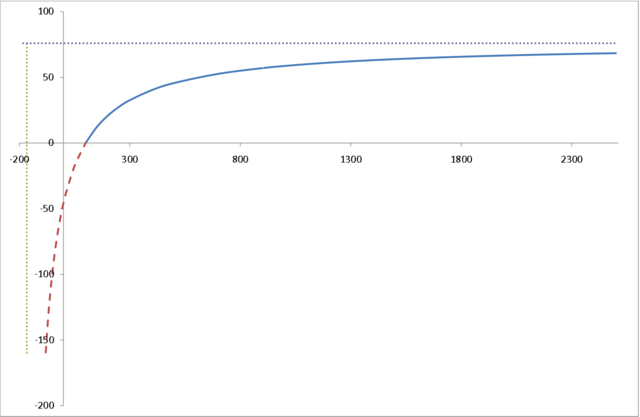
7.3.2. Funkcja Törnquista II typu
Funkcja Törnquista II typu wyraża zależność między popytem na dobra wyższego rzędu (![]() ), a dochodami konsumentów (
), a dochodami konsumentów (![]() )
)
Popyt rośnie wraz ze wzrostem dochodów i stabilizuje się na poziomie równym ![]() .
Wykres ma asymptotę poziomą.
Z drugiej strony popyt spada do zera wraz ze spadkiem dochodów i zanika dla dochodów niższych od granicznej wartości
.
Wykres ma asymptotę poziomą.
Z drugiej strony popyt spada do zera wraz ze spadkiem dochodów i zanika dla dochodów niższych od granicznej wartości ![]() .
.
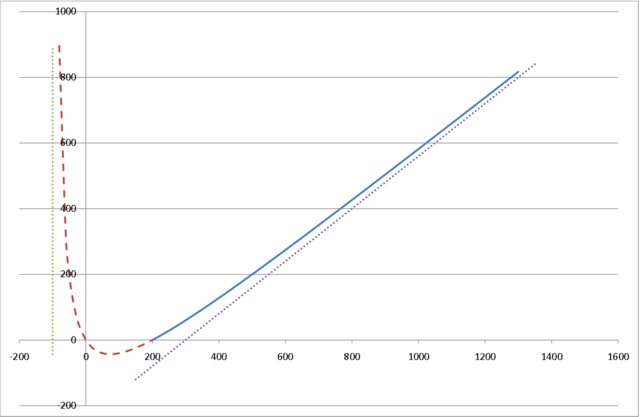
7.3.3. Funkcja Törnquista III typu
Funkcja Törnquista III typu wyraża zależność między popytem na dobra i usługi luksusowe (![]() ), a dochodami konsumentów (
), a dochodami konsumentów (![]() )
)
Popyt rośnie w sposób nieograniczony wraz ze wzrostem dochodów i dla dużych ![]() można go przybliżyć funkcją liniową
można go przybliżyć funkcją liniową
Wykres posiada asymptotę ukośną.
Z drugiej strony popyt spada do zera wraz ze spadkiem dochodów i zanika dla dochodów niższych od granicznej wartości ![]() .
.
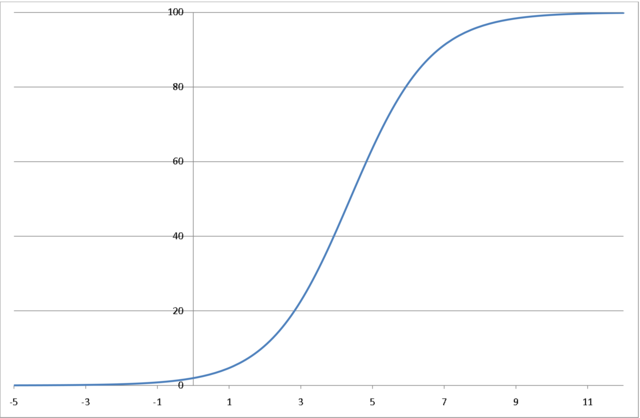
7.3.4. Funkcja logistyczna
Funkcja logistyczna wyraża zależność trendu wzrostowego ![]() od czasu
od czasu ![]()
Posiada ona następujące własności:![]() Jest ściśle rosnąca i przyjmuje wartości z przedziału
Jest ściśle rosnąca i przyjmuje wartości z przedziału ![]()
![]() Dla
Dla ![]() mamy
mamy ![]() .
.![]() Ma punkt przegięcia w
Ma punkt przegięcia w ![]() . Trend ma w okolicach tego punktu największe przyrosty.
. Trend ma w okolicach tego punktu największe przyrosty.![]() Jest rozwiązaniem równania różniczkowego o zmiennych rozdzielonych zwanego równaniem Robertsona
Jest rozwiązaniem równania różniczkowego o zmiennych rozdzielonych zwanego równaniem Robertsona
spełniającym warunek początkowy