Zagadnienia

9.1 Założenia modelu
9.2 Asymptotyka estymatorów MNK

9. Teoria dużej próbki

Teoria dużej próbki. Założenia modelu. Asymptotyczne własności estymatorów MNK. Statystyczna weryfikacja modelu. (2 wykłady)

9.1. Założenia modelu

W teorii dużej próbki przez model rozumie się $K+1$ wymiarowy proces stochastyczny

$\{(Y_{t},X_{t})\} _{{t=0}}^{\infty}$

spełniający pewne założenia.

Z̃1. Liniowość.

$\exists\beta\in\mathbb{R}^{K}\;\;\;\exists\{\varepsilon _{t}\} _{{t=0}}^{\infty}\;\;\; Y_{t}=X_{t}\beta+\varepsilon _{t},\;\;\; t=0,1,\dots,$

Z̃2. Stacjonarność i ergodyczność.
$K+1$ wymiarowy proces stochastyczny $\{(Y_{t},X_{t})\} _{{t=0}}^{\infty}$ jest stacjonarny i ergodyczny.

Uwaga.
Z warunków Z̃1 i Z̃2 wynika, że również proces $\{\varepsilon _{t}\} _{{t=0}}^{\infty}$ jest stacjonarny i ergodyczny.

Z̃3. Warunek maksymalnego rzędu.
Proces $X_{t}$ jest klasy $L^{2}$ i $K\times K$ macierz

$\Sigma _{{xx}}=E(X^{T}_{t}X_{t})$

jest odwracalna.

Uwaga.
Ze stacjonarności procesu $X_{t}$ wynika, że macierz $\Sigma _{{xx}}$ nie zależy od $t$ .

Z̃4. Ortogonalność zmiennych objaśniających do składnika losowego.

$E(\varepsilon _{t}X_{t})=0,\;\;\; t=0,1,\dots.$

Oznaczenie.

$g_{t}=\varepsilon _{t}X_{t}.$

Uwaga.
Z warunków Z̃1 i Z̃2 wynika, że również proces $\{ g_{t}\} _{{t=0}}^{\infty}$ jest stacjonarny i ergodyczny.

Z̃5. Martyngałowość.
Proces $\{ g_{t}\} _{{t=0}}^{\infty}$ jest ciągiem przyrostów martyngałowych, $g_{t}$ jest klasy $L^{2}$ i $K\times K$ macierz

$\Sigma _{{gg}}=E(g^{T}_{t}g_{t})$

jest odwracalna.

Uwaga.
1. Ze stacjonarności procesu $g_{t}$ wynika, że macierz $\Sigma _{{gg}}$ nie zależy od $t$ .
2. Z centralnego twierdzenia granicznego (8.6) wynika , że $\Sigma _{{gg}}$ jest równa asymptotycznej wariancji procesu średnich $\bar{g}_{t}$

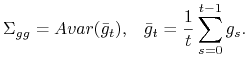$\Sigma _{{gg}}=Avar(\bar{g}_{t}),\;\;\;\bar{g}_{t}=\frac{1}{t}\sum _{{s=0}}^{{t-1}}g_{s}.$

Z̃6. Warunkowa homoskedastyczność.

$E(\varepsilon _{t}^{2}|X_{t})=\sigma^{2}>0,\;\;\; t=0,1,\dots.$

Lemat 9.1

Z warunków Z̃2 i Z̃6 wynika, że

$\Sigma _{{gg}}=\sigma^{2}\Sigma _{{xx}}.$

Dowód.
$g_{t}=\varepsilon _{t}X_{t}$ , zatem

$\Sigma _{{gg}}=E(g^{T}_{t}g_{t})=E(\varepsilon^{2}X_{t}^{T}X_{t})=E(E(\varepsilon _{t}^{2}X_{t}^{T}X_{t}|X_{t}))=$

$=E(E(\varepsilon^{2}_{t}|X_{t})X_{t}^{T}X_{t})=E(\sigma^{2}X_{t}^{T}X_{t})=\sigma^{2}E(X_{t}^{T}X_{t})=\sigma^{2}\Sigma _{{xx}}.$

$\Box$

Uwaga 9.1

Aksjomaty Z̃ modelu dużej próbki (poza Z̃2) są słabsze od aksjomatów Z modelu klasycznego. Otóż, niech $\{(Y_{t},X_{t})\} _{{t=0}}^{\infty}$ będzie $K+1$ wymiarowym, klasy $L^{2}$ , stacjonarnym i ergodycznym procesem stochastycznym, wówczas jeśli dla każdego $n>K$ jego początkowy fragment $\{(Y_{t},X_{t})\} _{{t=0}}^{n}$ spełnia aksjomaty Z1, Z2, Z3, Z4 i Z5 to spełnia on Z̃1, Z̃2, Z̃3, Z̃4, Z̃5 i Z̃6.

9.2. Asymptotyka estymatorów MNK

Niech $\{(Y_{t},X_{t})\} _{{t=0}}^{\infty}$ będzie procesem generującym dane. W modelu dużej próbki, podobnie jak w modelu klasycznym, będziemy estymowali parametry modelu $\beta$ i $\sigma^{2}$ w oparciu o metodę najmniejszym kwadratów. Niech $n$ oznacza ilość obserwacji ( $n\gg K$ ), $X$ macierz wymiaru $n\times K$ , której wierszami są wektory losowe $X_{t}$ a $Y$ wektor kolumnowy wymiaru $n$ o wyrazach $Y_{t}$ . Estymatory MNK możemy zapisać na dwa sposoby jako iloczyn macierzy $X$ i $Y$ lub za pomocą średnich z iloczynów $X_{t}$ i $Y_{t}$ .

Gdy macierz $X$ ma rząd maksymalny czyli $K$ , to estymator MNK wektora $\beta$ wynosi

$B=(X^{T}X)^{{-1}}X^{T}Y=S_{{xx}}^{{-1}}S_{{xy}},$

gdzie

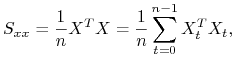$S_{{xx}}=\frac{1}{n}X^{T}X=\frac{1}{n}\sum _{{t=0}}^{{n-1}}X_{t}^{T}X_{t},$

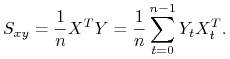$S_{{xy}}=\frac{1}{n}X^{T}Y=\frac{1}{n}\sum _{{t=0}}^{{n-1}}Y_{t}X_{t}^{T}.$

W wyjątkowych przypadkach gdy rząd macierzy $X$ jest mniejszy niż $K$ to jako $B$ bierzemy dowolny wektor minimalizujący sumę kwadratów reszt – patrz uwaga 2.1.

Natomiast estymator MNK parametru $\sigma^{2}$ wynosi

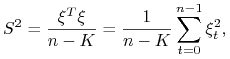$S^{2}=\frac{\xi^{T}\xi}{n-K}=\frac{1}{n-K}\sum _{{t=0}}^{{n-1}}\xi _{t}^{2},$

gdzie

$\xi _{t}=Y_{t}-X_{t}B.$

Omówimy teraz podstawowe własności powyższych estymatorów w zależności od wielkości próbki $n$ .

Twierdzenie 9.1

Własności estymatorów $B$ i $S^{2}$ :
a. Zgodność $B$

$\mbox{\~{Z1} -- \~{Z4}}\Longrightarrow\lim _{{n\rightarrow\infty}}B=\beta\;\;\; p.n.$

b. Asymptotyczna normalność $B$

$\mbox{\~{Z1} -- \~{Z5}}\Longrightarrow\sqrt{n}(B-\beta)\stackrel{d}{\longrightarrow}N(0,Avar(B)),$

gdzie

$Avar(B)=\Sigma _{{xx}}^{{-1}}\Sigma _{{gg}}\Sigma _{{xx}}^{{-1}}.$

Jeśli dodatkowo założymy Z̃6, to

$Avar(B)=\sigma^{2}\Sigma _{{xx}}^{{-1}}.$

c. Zgodność $S^{2}$

$\mbox{\~{Z1} -- \~{Z4}}\Longrightarrow\lim _{{n\rightarrow\infty}}S^{2}=E(\varepsilon _{0}^{2})\;\;\; p.n.$

Jeśli dodatkowo założymy Z̃6, to

$\mathop{\mathrm{plim}}\displaylimits _{{n\rightarrow\infty}}S^{2}=\sigma^{2}.$

d. Zgodna estymacja $Avar(B)$

$\mbox{\~{Z1} -- \~{Z6}}\Longrightarrow\lim _{{n\rightarrow\infty}}S^{2}S_{{xx}}^{{-1}}=Avar(B)\;\;\; p.n.$

Dowód.
Mamy dwa równania opisujące zależność $Y_{t}$ od $X_{t}$ :

	$\displaystyle Y_{t}$	$\displaystyle=$	$\displaystyle X_{t}\beta+\varepsilon _{t},$
	$\displaystyle Y_{t}$	$\displaystyle=$	$\displaystyle X_{t}B+\xi _{t}.$

Po odjęciu stronami otrzymujemy:

$X_{t}(B-\beta)=\varepsilon _{t}-\xi _{t}.$

(9.1)

Mnożymy obie strony przez $X_{t}^{T}$

$X_{t}^{T}X_{t}(B-\beta)=\varepsilon _{t}X_{t}^{T}-\xi _{t}X_{t}^{T}.$

Następnie liczymy średnią po $t$ . Biorąc pod uwagę, że $\sum _{{t=0}}^{{n-1}}\xi _{t}X_{t}^{T}=X^{T}\xi=0$ (patrz wniosek 2.1) otrzymujemy:

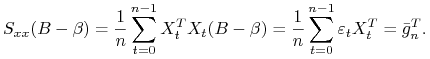$S_{{xx}}(B-\beta)=\frac{1}{n}\sum _{{t=0}}^{{n-1}}X_{t}^{T}X_{t}(B-\beta)=\frac{1}{n}\sum _{{t=0}}^{{n-1}}\varepsilon _{t}X_{t}^{T}=\bar{g}_{n}^{T}.$

Ponieważ proces $X_{t}^{T}X_{t}$ jest stacjonarny i ergodyczny to

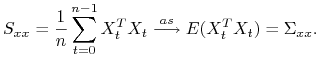$S_{{xx}}=\frac{1}{n}\sum _{{t=0}}^{{n-1}}X_{t}^{T}X_{t}\stackrel{as}{\longrightarrow}E(X_{t}^{T}X_{t})=\Sigma _{{xx}}.$

Macierz $\Sigma _{{xx}}$ jest odwracalna (warunek Z̃3), zatem dla dużych $n$ również macierz $S_{{xx}}(\omega)$ jest odwracalna. W wyjątkowych przypadkach gdy $\det S_{{xx}}(\omega)=0$ dookreślamy $S_{{xx}}^{{-1}}(\omega)$ w dowolny sposób.

Po przemnożeniu obu stron przez macierz $S_{{xx}}^{{-1}}$ otrzymujemy równość analogiczną do 4.2

$B-\beta=S_{{xx}}^{{-1}}\bar{g}_{n}+\gamma _{n},$

(9.2)

gdzie $\gamma _{n}(\omega)=0$ dla $n$ odpowiednio dużych.

Ad. a.
Ponieważ proces $g_{t}$ jest stacjonarny i ergodyczny to z warunku Z̃4 otrzymujemy

$\lim _{{n\rightarrow\infty}}\bar{g}_{n}=E(g_{0})=0\;\;\; p.n.$

Zatem

$\lim _{{n\rightarrow\infty}}B-\beta=\lim _{{n\rightarrow\infty}}S_{{xx}}^{{-1}}\bar{g}_{n}=\Sigma _{{xx}}^{{-1}}0=0\;\;\; p.n.$

Ad. b.
Proces $g_{t}$ oprócz tego, że jest stacjonarny i ergodyczny to jest ciągiem przyrostów martyngałowych, a więc ((8.6))

$\sqrt{n}\bar{g}\stackrel{d}{\longrightarrow}N(0,\Sigma _{{gg}}).$

Zatem

$\sqrt{n}(B-\beta)\stackrel{d}{\longrightarrow}N(0,\Sigma _{{xx}}^{{-1}}\Sigma _{{gg}}\Sigma _{{xx}}^{{-1}}).$

Jeśli ponadto założymy Z̃6 to

$\Sigma _{{gg}}=\sigma^{2}\Sigma _{{xx}},$

zatem

$Avar(B)=\Sigma _{{xx}}^{{-1}}\Sigma _{{gg}}\Sigma _{{xx}}^{{-1}}=\Sigma _{{xx}}^{{-1}}(\sigma^{2}\Sigma _{{xx}})\Sigma _{{xx}}^{{-1}}=\sigma^{2}\Sigma _{{xx}}^{{-1}}.$

Ad. c.
Przepisując odpowiednio równanie 9.1 otrzymujemy

$\xi _{t}=\varepsilon _{t}-X_{t}(B-\beta).$

Zatem

$\xi^{2}_{t}=\varepsilon _{t}^{2}-2g_{t}(B-\beta)+(B-\beta)^{T}X_{t}^{T}X_{t}(B-\beta).$

Po uśrednieniu otrzymujemy

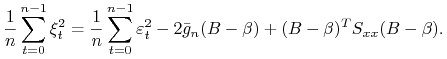$\frac{1}{n}\sum _{{t=0}}^{{n-1}}\xi _{t}^{2}=\frac{1}{n}\sum _{{t=0}}^{{n-1}}\varepsilon _{t}^{2}-2\bar{g}_{n}(B-\beta)+(B-\beta)^{T}S_{{xx}}(B-\beta).$

Przechodzimy do granicy. Ponieważ

$\lim _{{n\rightarrow\infty}}B-\beta=0=\lim _{{n\rightarrow\infty}}\bar{g}_{n},\;\;\;\mbox{ oraz }\;\;\;\lim _{{n\rightarrow\infty}}S_{{xx}}=\Sigma _{{xx}}\;\;\; p.n.,$

to otrzymujemy, że

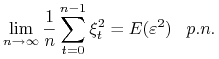$\lim _{{n\rightarrow\infty}}\frac{1}{n}\sum _{{t=0}}^{{n-1}}\xi _{t}^{2}=E(\varepsilon^{2})\;\;\; p.n.$

Zatem

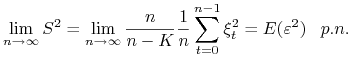$\lim _{{n\rightarrow\infty}}S^{2}=\lim _{{n\rightarrow\infty}}\frac{n}{n-K}\frac{1}{n}\sum _{{t=0}}^{{n-1}}\xi _{t}^{2}=E(\varepsilon^{2})\;\;\; p.n.$