Zagadnienia
12. Przestrzeń barw i jej układy współrzędnych
12.1. Podstawy kolorymetrii
Światło jest promieniowaniem elektromagnetycznym o długości fali
![]() –
–![]() nm. Barwa światła jest określona przez jego widmo, czyli
funkcję opisującą rozkład energii niesionej przez światło
w zależności od długości fali.
nm. Barwa światła jest określona przez jego widmo, czyli
funkcję opisującą rozkład energii niesionej przez światło
w zależności od długości fali.
Natura wyposażyła ludzi w receptory światła (tzw. czopki) trzech różnych rodzajów. Każdy z nich ma maksimum czułości odpowiadające innej długości fali światła12Oprócz czopków mamy też tzw. pręciki, które są czulsze od czopków, ale nie rozróżniają barw. Wskutek tego w słabym oświetleniu (np. o zmroku) oglądane przedmioty są bezbarwne.. Dlatego przestrzeń wrażeń wywoływanych u ludzi przez światło (tj. sygnałów przesyłanych przez receptory do mózgu) jest trójwymiarowa13U innych gatunków bywa inaczej, np. przestrzeń wrażeń barwnych rozróżnianych przez krowę jest tylko dwuwymiarowa, natomiast morskie skorupiaki z gatunku rawka wieszcza (Squilla mantis) mają dziesięć różnych typów receptorów światła (w tym receptory czułe na polaryzację).. Inaczej mówiąc, można otrzymać dowolne wrażenie barwne przez zmieszanie światła w trzech tzw. barwach podstawowych (z zastrzeżeniem, o którym dalej).
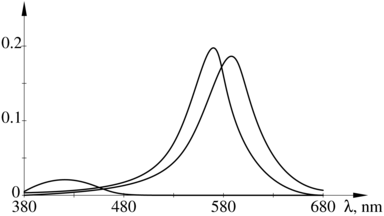
Dla poszczególnych rodzajów czopków można znaleźć wykresy ich czułości na światło zależnie od długości fali. Energia światła zaabsorbowanego przez receptor (czyli ,,intensywność wrażenia wzrokowego”) jest całką z iloczynu widma padającego nań światła i jego funkcji czułości. Mając źródła światła o znanych widmach (np. czerwony, zielony i niebieski luminofor w ekranie monitora) możemy, dobierając odpowiednio moc ich świecenia, tak pobudzać receptory, aby ich reakcja była taka sama jak na światło pochodzące z danego źródła.
Jeśli ustalimy moc (intensywność) światła i będziemy zmieniać widmo,
to dla ustalonych trzech barw podstawowych możemy wykonać rysunek
dwuwymiarowy. Barwy podstawowe znajdą się w wierzchołkach trójkąta;
ich intensywności (o stałej sumie, unormowanej do ![]() ) są
współrzędnymi barycentrycznymi
punktu odpowiedającego danemu światłu. Wypełniając trójkąt barwami
(wykonując cieniowanie metodą Gourauda), otrzymamy obrazek
zawierający wszystkie barwy możliwe do otrzymania przez zmieszanie barw
podstawowych. Barwy reprezentowane przez punkty na zewnątrz trójkąta
mają określone współrzędne, ale otrzymanie ich przez zmieszanie barw
podstawowych jest fizycznie niewykonalne.
) są
współrzędnymi barycentrycznymi
punktu odpowiedającego danemu światłu. Wypełniając trójkąt barwami
(wykonując cieniowanie metodą Gourauda), otrzymamy obrazek
zawierający wszystkie barwy możliwe do otrzymania przez zmieszanie barw
podstawowych. Barwy reprezentowane przez punkty na zewnątrz trójkąta
mają określone współrzędne, ale otrzymanie ich przez zmieszanie barw
podstawowych jest fizycznie niewykonalne.
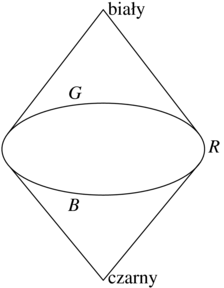
Pomiar współrzędnych barwy danego światła przeprowadza się za pomocą kolorymetru. Zawiera on trzy źrodła światła wzorcowego; lampę czerwoną, czyli żarówkę z filtrem, oraz dwie lampy rtęciowe, wytwarzające światło zielone i niebieskie. Osoba dokonująca pomiaru tak ustawia przysłony źródeł światła wzorcowego, aby ściany białego klina były (jej zdaniem) identycznie oświetlone przez światło badane i wzorcowe. Współrzędne barwy odczytuje się z podziałek na przysłonach. Aby umożliwić pomiar ujemnych współrzędnych barwy (dla światła, którego nie można otrzymać, mieszając światła wzorcowe), kolorymetr jest wyposażony w źródła światła wzorcowego z przysłonami także od strony okienka, przez które wpada światło badane.
12.2. Diagram CIE
Dla danego widma może istnieć tzw. dominująca długość fali. Gdyby światło obserwowane przez oko było mieszaniną (w odpowiednich proporcjach) światła o tej długości fali ze światłem białym14Określenie ,,światło białe” jest niejednoznaczne, przez co jest źródłem wielu nieporozumień. Można umawiać się, że jest to światło o stałym widmie w całym zakresie długości fali albo światło wysyłane przez ,,ciało doskonale czarne” o ustalonej temperaturze. Chwilowo stosuję pierwszą umowę., to wrażenia byłyby identyczne jak wrażenia wywołane przez światło o danym widmie. Światło białe jest rozszczepiane przez pryzmat na tęczę. Poszczególne barwy tęczy odpowiadają różnym dominującym długościom fali.
Jedną z podstaw postępu technicznego jest standaryzacja. W zastosowaniach
technicznych podstawą do opracowywania standardów jest powszechnie
używany diagram CIE, ustalony w 1931r. przez Międzynarodową
Komisję Oświetleniową (Commision Internationale de l'Eclairage),
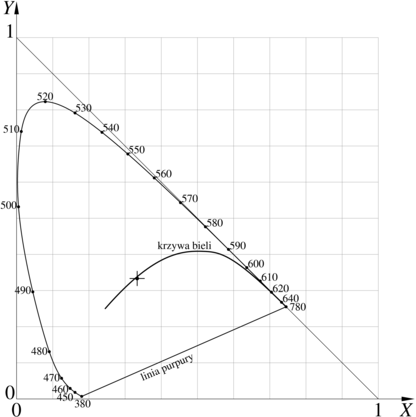
przedstawiony na rysunku 12.3.
Układ współrzędnych barw, w którym jest przedstawiany ten diagram,
będący także podstawą do określania innych układów współrzędnych
w przestrzeni barw, nazywa się układem ![]() . Obszar płaszczyzny,
który reprezentuje barwy widzialne, ma kształt podkowy15Z moich obserwacji wynika, że końska podkowa ma inny kształt,
ale wszystkie opisy diagramu CIE, a więc i ten, zawierają wzmiankę
o podkowie.
wpisanej w trójkąt, którego wierzchołki
stanowią układ odniesienia. Dzięki temu współrzędne wszystkich
widzialnych barw w układzie
. Obszar płaszczyzny,
który reprezentuje barwy widzialne, ma kształt podkowy15Z moich obserwacji wynika, że końska podkowa ma inny kształt,
ale wszystkie opisy diagramu CIE, a więc i ten, zawierają wzmiankę
o podkowie.
wpisanej w trójkąt, którego wierzchołki
stanowią układ odniesienia. Dzięki temu współrzędne wszystkich
widzialnych barw w układzie ![]() są nieujemne.
są nieujemne.
Punkty na krzywej ograniczającej diagram od góry odpowiadają barwom światła monochromatycznego (w którym występują tylko fale o jednej długości). Na krzywej tej leżą kolejne barwy tęczy. Odcinek ograniczający diagram od dołu to tzw. linia purpury. Światło reprezentowane przez punkty tego odcinka jest mieszaniną światła fioletowego i czerwonego i nie można dla niego wskazać dominującej długości fali. Punkty wewnątrz diagramu reprezentują światło ,,złamane”, z domieszką bieli.
Uwaga: Światło o barwie reprezentowanej przez punkty spoza obszaru ograniczonego krzywą tęczy i linią purpury nie istnieje. Także barwy określające układ odniesienia są tylko umowne, wbrew temu, co można przeczytać w niektórych publikacjach. Ponieważ obszar reprezentujący barwy światła widzialnego nie jest wielokątem, więc nie istnieje żaden skończony zbiór źródeł światła, którego mieszanie pozwoliłoby otrzymać wszystkie widzialne barwy (ale jest oczywiste, dlaczego obszar ten jest wypukły).
Płaski obrazek umożliwia przedstawienie pewnego przekroju trójwymiarowego
zbioru wrażeń rozróżnianych przez ludzki narząd wzroku;
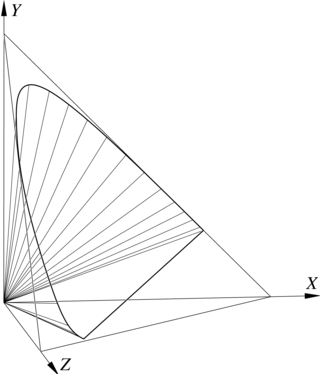
diagram CIE przedstawia światło o stałej mocy. Bryła, której punkty
reprezentują światło widzialne o ograniczonej mocy całkowitej,
przedstawiona w układzie ![]() , jest pokazana na rysunku 12.4.
, jest pokazana na rysunku 12.4.
Pojęcie bieli jest umowne, ponieważ oko przyzwyczaja się do
różnych warunków oświetlenia i odbiera jako ,,białe” światło
o różnych barwach. Na ogół za białe przyjmuje się światło wysyłane
przez ciało doskonale czarne (np. pogrzebacz, żarówka, Słońce),
ogrzane do odpowiedniej temperatury (np. pogrzebacz — ![]() K,
żarówka —
K,
żarówka — ![]() K, Słońce —
K, Słońce — ![]() K, oświetlenie przez
promienie słoneczne rozproszone w atmosferze —
K, oświetlenie przez
promienie słoneczne rozproszone w atmosferze — ![]() K).
Na diagramie CIE barwy światła białego o różnych temperaturach
leżą na pewnej krzywej (uwidocznionej na rysunku 12.3).
K).
Na diagramie CIE barwy światła białego o różnych temperaturach
leżą na pewnej krzywej (uwidocznionej na rysunku 12.3).
Mając ustaloną barwę białą można wprowadzić pojęcia
nasycenia barwy i barwy dopełniającej. Barwa jest
nasycona wtedy, gdy reprezentujący ją punkt leży na brzegu obszaru barw
widzialnych. Nasycenie jest równe ![]() wtedy, gdy światło jest białe
i
wtedy, gdy światło jest białe
i ![]() jeśli odpowiedni punkt znajduje się na brzegu obszaru barw
widzialnych. Dla ustalonej
barwy można narysować prostą przechodzącą przez reprezentujący ją
punkt i punkt bieli. Nasycenie można odczytać mierząc proporcję
podziału odcinka łączącego punkt bieli z brzegiem obszaru, przez punkt
reprezentujący barwę daną.
Barwa dopełniająca jest reprezentowana przez pewien punkt na rozpatrywanej
prostej po przeciwnej stronie punktu bieli. Ma ona to samo nasycenie
i moc, co barwa przez nią dopełniana.
jeśli odpowiedni punkt znajduje się na brzegu obszaru barw
widzialnych. Dla ustalonej
barwy można narysować prostą przechodzącą przez reprezentujący ją
punkt i punkt bieli. Nasycenie można odczytać mierząc proporcję
podziału odcinka łączącego punkt bieli z brzegiem obszaru, przez punkt
reprezentujący barwę daną.
Barwa dopełniająca jest reprezentowana przez pewien punkt na rozpatrywanej
prostej po przeciwnej stronie punktu bieli. Ma ona to samo nasycenie
i moc, co barwa przez nią dopełniana.
Różne urządzenia mają różne zbiory barw, które mogą reprodukować. Na przykład telewizory i monitory komputerowe z lampą kineskopową mają trzy rodzaje luminoforów, które świecąc z różną intensywnością, zawsze nieujemną, odwzorowują barwy reprezentowane przez punkty należące do trójkąta, którego wierzchołki odpowiadają barwom światła wysyłanego przez poszczególne luminofory. Drukarki kolorowe mają co najmniej trzy różne atramenty, co teoretycznie umożliwia reprodukcję barwy o dowolnym odcieniu. Częściej jednak atramentów jest więcej (np. sześć), ponieważ dla otrzymania wydruku o dobrej jakości potrzebne jest uzyskanie barw o wysokim nasyceniu, a to jest trudne dla barw otrzymanych przez zmieszanie różnych atramentów, których barwy są odległe od barw reprodukowanych. Zwykle zbiór barw możliwych do wydrukowania nie zawiera, ani nie jest zawarty w zbiorze barw możliwych do otrzymania na monitorze. Oczywiście, zadrukowany papier nie jest źródłem światła, tylko obiektem odbijającym światło, a zatem reprodukcja barw przez urządzenia drukujące jest zależna od światła, w jakim obraz oglądamy. Zwróćmy jednak uwagę, że wzrok osoby oglądającej wydrukowany obrazek przyzwyczaja się do światła w otoczeniu (przez co uważamy, że ,,biała” kartka papieru wygląda tak samo w świetle dziennym i sztucznym).
Tworzenie i przesyłanie obrazu wiąże się z błędami reprezentacji barw. Konieczne jest zatem zbadanie następującego problemu: na jakie zniekształcenia barw ludzki wzrok jest najbardziej i najmniej wyczulony?
Odpowiedź na to pytanie ma znaczenie dla opracowania metod transmisji (w tym kompresji) obrazów i dla reprodukcji obrazu na urządzeniu, które nie może oddać wszystkich barw obecnych w obrazie danym. W dużym uproszczeniu można stwierdzić, że najmniej dostrzegalne są zmiany nasycenia i jasności całego obrazu, a najbardziej widoczne są różne zmiany odcienia (czyli długości fali dominującej) oraz różne zmiany jasności sąsiednich obszarów. Z tego powodu, aby wydrukować obraz na drukarce, która nie odtwarza takich barw jak monitor, trzeba dokonać tzw. desaturacji obrazu — wszystkie punkty reprezentujące barwy na obrazie będą ,,przesunięte” w stronę bieli.
12.3. Współrzędne 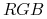 i
i 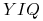
W praktyce (telewizyjno-komputerowej) zamiast współrzędnych ![]() stosuje
się współrzędne
stosuje
się współrzędne ![]() , które mają związek z barwami światła
emitowanego przez luminofory w kineskopach.
W tabeli niżej są współrzędne
, które mają związek z barwami światła
emitowanego przez luminofory w kineskopach.
W tabeli niżej są współrzędne ![]() ,
, ![]() punktów odniesienia układu
punktów odniesienia układu
![]() w standardach NTSC i CIE, a także barwy luminoforów w typowym
monitorze.
w standardach NTSC i CIE, a także barwy luminoforów w typowym
monitorze.
| NTSC | CIE | monitor | |
|---|---|---|---|
Do transmisji obrazów (w telewizji) stosuje się układ ![]() , w którym
podaje się wartość tzw. luminancji
, w którym
podaje się wartość tzw. luminancji ![]() i dwie wartości
chrominancji,
i dwie wartości
chrominancji, ![]() ,
, ![]() . Sygnał luminancji wystarczy do utworzenia
obrazu na ekranie telewizora czarno-białego.
. Sygnał luminancji wystarczy do utworzenia
obrazu na ekranie telewizora czarno-białego.
Aby obliczyć współrzędne ![]() znając
znając ![]() i odwrotnie, stosuje się
następujące wzory (tu jest NTSC
i odwrotnie, stosuje się
następujące wzory (tu jest NTSC ![]() ):
):
![\displaystyle\left[\begin{array}[]{c}Y\\
I\\
Q\end{array}\right]](wyklady/gk1/mi/mi1085.png) |
![\displaystyle=\left[\begin{array}[]{ccc}0.299&0.587&0.144\\
0.596&-0.275&0.321\\
0.212&-0.528&0.311\end{array}\right]\left[\begin{array}[]{c}R\\
G\\
B\end{array}\right]](wyklady/gk1/mi/mi1079.png) |
||
![\displaystyle\left[\begin{array}[]{c}R\\
G\\
B\end{array}\right]](wyklady/gk1/mi/mi1070.png) |
![\displaystyle=\left[\begin{array}[]{ccc}1&0.956&0.62\\
1&-0.272&-0.647\\
1&-1.108&1.705\end{array}\right]\left[\begin{array}[]{c}Y\\
I\\
Q\end{array}\right].](wyklady/gk1/mi/mi1059.png) |
Okazuje się, że w obrazach telewizyjnych do przesyłania sygnału ![]() wystarczy pasmo o szerokości
wystarczy pasmo o szerokości ![]() MHz, a dla sygnałów
MHz, a dla sygnałów ![]() oraz
oraz ![]() odpowiednio
odpowiednio ![]() MHz i
MHz i ![]() MHz.
Wynikające stąd zniekształcenia obrazów
są dostatecznie małe w telewizji16Ale utworzenie obrazu na ekranie monitora komputerowego o wysokiej
rozdzielczości wymaga wyświetlania pikseli w tempie od
MHz.
Wynikające stąd zniekształcenia obrazów
są dostatecznie małe w telewizji16Ale utworzenie obrazu na ekranie monitora komputerowego o wysokiej
rozdzielczości wymaga wyświetlania pikseli w tempie od ![]() do
do ![]() MHz;
w przeciwnym razie małe literki byłyby nieczytelne. Także tzw. telewizja
HDTV wymaga przesyłania sygnałów o znacznie szerszych pasmach. W tym celu
sygnał w postaci cyfrowej poddaje się kompresji stratnej, dzięki czemu
nie trzeba wykorzystywać aż tak szerokich pasm, niedostępnych z powodów
technicznych..
Również wiele algorytmów stratnej
kompresji obrazu (np. JPEG) reprezentuje obraz we współrzędnych
MHz;
w przeciwnym razie małe literki byłyby nieczytelne. Także tzw. telewizja
HDTV wymaga przesyłania sygnałów o znacznie szerszych pasmach. W tym celu
sygnał w postaci cyfrowej poddaje się kompresji stratnej, dzięki czemu
nie trzeba wykorzystywać aż tak szerokich pasm, niedostępnych z powodów
technicznych..
Również wiele algorytmów stratnej
kompresji obrazu (np. JPEG) reprezentuje obraz we współrzędnych ![]() i koduje każdą składową osobno, dopuszczając większe zniekształcenia
dla składowych chrominancji i osiągając dzięki temu większy
współczynnik kompresji przy zachowaniu subiektywnie dobrej jakości
obrazu.
i koduje każdą składową osobno, dopuszczając większe zniekształcenia
dla składowych chrominancji i osiągając dzięki temu większy
współczynnik kompresji przy zachowaniu subiektywnie dobrej jakości
obrazu.
12.4. Współrzędne 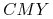 i
i 
Współrzędne ![]() , a także
, a także ![]() i
i ![]() , są związane z modelem
addytywnego mieszania światła. W drukarstwie i fotografii
ma zastosowanie też model subtraktywny, z którym związane
są układy współrzędnych
, są związane z modelem
addytywnego mieszania światła. W drukarstwie i fotografii
ma zastosowanie też model subtraktywny, z którym związane
są układy współrzędnych ![]() i
i ![]() . Symbole współrzędnych
pochodzą od angielskich nazw barw podstawowych
(Cyan — niebieskozielony, Magenta — purpurowy,
Yellow — żółty). Zasada subtraktywnego mieszania barw jest
taka, że światło białe przechodzi przez barwne filtry,
które je tłumią. Jeśli więc
. Symbole współrzędnych
pochodzą od angielskich nazw barw podstawowych
(Cyan — niebieskozielony, Magenta — purpurowy,
Yellow — żółty). Zasada subtraktywnego mieszania barw jest
taka, że światło białe przechodzi przez barwne filtry,
które je tłumią. Jeśli więc ![]() , to mamy światło białe,
jeśli
, to mamy światło białe,
jeśli ![]() ,
, ![]() to światło żółte (żółty filtr,
to światło żółte (żółty filtr, ![]() , nie
przepuszcza światła niebieskiego),
, nie
przepuszcza światła niebieskiego), ![]() ,
, ![]() opisuje światło
czerwone (filtr purpurowy,
opisuje światło
czerwone (filtr purpurowy, ![]() , zatrzymuje światło zielone) i dla
, zatrzymuje światło zielone) i dla
![]() otrzymujemy czerń.
otrzymujemy czerń.
Ponieważ barwniki, którymi drukuje się obrazy, nie są idealnymi
filtrami, więc nawet przy ich maksymalnym stężeniu w danym miejscu pewna
ilość światła przechodzi przez warstwę farby lub atramentu (dwukrotnie,
w międzyczasie odbijając się od białego papieru) i nie otrzymujemy
idealnej czerni (tylko jakiś bury kolor). Dlatego stosuje się model
![]() , w którym czwarta współrzędna,
, w którym czwarta współrzędna, ![]() (ang. blacK) opisuje
stężenie czarnej farby. Teoretycznie, mając współrzędne
(ang. blacK) opisuje
stężenie czarnej farby. Teoretycznie, mając współrzędne ![]() ,
, ![]() ,
, ![]() ,
obliczamy
,
obliczamy
Jedna ze współrzędnych ![]() ,
, ![]() ,
, ![]() otrzyma wartość
otrzyma wartość ![]() .
.
W praktyce często przyjmuje się mniejszą
wartość ![]() , co poprawia końcowy efekt, ponieważ m.in. domieszanie
niewielkiej ilości czarnej farby do pozostałych ,,zabrudziłoby” barwę
wydrukowanego obrazu. Ponadto, z uwagi na nieuniknione przesunięcia
wydruków w poszczególnych barwach, czarny nadruk na kolorowym tle może
,,nie trafić” w odpowedni biały obszar otoczony tłem i widać białą
,,obwódkę” dookoła czarnego obszaru. Aby temu przeciwdziałać należy
tło wydrukować bez ,,otworu” na czarną farbę, której naniesienie nieco
obok właściwego miejsca będzie dzięki temu niedostrzegalne. Z tego
przykładu wynika, że przejście od współrzędnych
, co poprawia końcowy efekt, ponieważ m.in. domieszanie
niewielkiej ilości czarnej farby do pozostałych ,,zabrudziłoby” barwę
wydrukowanego obrazu. Ponadto, z uwagi na nieuniknione przesunięcia
wydruków w poszczególnych barwach, czarny nadruk na kolorowym tle może
,,nie trafić” w odpowedni biały obszar otoczony tłem i widać białą
,,obwódkę” dookoła czarnego obszaru. Aby temu przeciwdziałać należy
tło wydrukować bez ,,otworu” na czarną farbę, której naniesienie nieco
obok właściwego miejsca będzie dzięki temu niedostrzegalne. Z tego
przykładu wynika, że przejście od współrzędnych ![]() do
do ![]() w celu
otrzymania wyciągów barwnych do drukowania jest trywialne tylko pozornie.
w celu
otrzymania wyciągów barwnych do drukowania jest trywialne tylko pozornie.
Warto pamiętać, że zagadnienia związane z mieszaniem farb drukarskich
lub atramentów na papierze są bardzo skomplikowane i dlatego przygotowanie
obrazu do druku w celu otrzymania takiej jak trzeba ilości farby na
papierze jest sztuką trudną. Stanowi ona przedmiot intensywnych badań
firm produkujących maszyny drukarskie i drukarki. Firmy te starannie
chronią swoje tajemnice przemysłowe. Ponieważ współrzędne ![]() są
ściśle związane z określoną technologią (tj. na przykład
z przygotowaniem filmów do naświetlania form drukarskich), więc ich
praktyczna przydatność dla użytkowników grafiki (z wyjątkiem osób
przygotowujących ilustracje do druku) jest raczej niewielka (ale warto
wiedzieć, o co może chodzić pracownikowi firmy poligraficznej, z którym
będziemy współpracować).
są
ściśle związane z określoną technologią (tj. na przykład
z przygotowaniem filmów do naświetlania form drukarskich), więc ich
praktyczna przydatność dla użytkowników grafiki (z wyjątkiem osób
przygotowujących ilustracje do druku) jest raczej niewielka (ale warto
wiedzieć, o co może chodzić pracownikowi firmy poligraficznej, z którym
będziemy współpracować).
12.5. Współrzędne  i
i 
Współrzędne ![]() są wygodne w technice (w konstrukcji monitorów), ale
dla potrzeb interakcyjnego dobierania barw są one mało intuicyjne. Dla
użytkowników programów graficznych (zwłaszcza dla osób, których
wykształcenie techniczne nie dorównuje plastycznemu) znacznie
wygodniejszy jest układ współrzędnych
są wygodne w technice (w konstrukcji monitorów), ale
dla potrzeb interakcyjnego dobierania barw są one mało intuicyjne. Dla
użytkowników programów graficznych (zwłaszcza dla osób, których
wykształcenie techniczne nie dorównuje plastycznemu) znacznie
wygodniejszy jest układ współrzędnych ![]() (nazwy współrzędnych są
wzięte z angielskiego: Hue oznacza
odcień, Saturation — nasycenie17Nasycenie w tym układzie jest określone względem bryły barw
fizycznie realizowalnych. Wartość
(nazwy współrzędnych są
wzięte z angielskiego: Hue oznacza
odcień, Saturation — nasycenie17Nasycenie w tym układzie jest określone względem bryły barw
fizycznie realizowalnych. Wartość ![]() nasycenia odpowiada więc
barwom o maksymalnym nasyceniu możliwym do uzyskania na danym urządzeniu,
mimo że te barwy leżą wewnątrz obszaru barw widzialnych przedstawionego
za pomocą diagramu CIE.,
Value — wartość).
nasycenia odpowiada więc
barwom o maksymalnym nasyceniu możliwym do uzyskania na danym urządzeniu,
mimo że te barwy leżą wewnątrz obszaru barw widzialnych przedstawionego
za pomocą diagramu CIE.,
Value — wartość).
Zbiór barw możliwych do osiągnięcia na monitorze można przedstawić
jako sześcian; współrzędne ![]() ,
, ![]() ,
, ![]() zmieniają się od
zmieniają się od ![]() do
do ![]() wzdłuż jego krawędzi. Tę bryłę barw można poddać
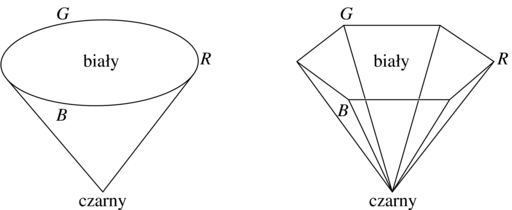
nieliniowemu przekształceniu, w wyniku którego powstaje stożek. Czasem
też przedstawia się tę bryłę jako ostrosłup sześciokątny, być może
dlatego, że łatwiej jest go narysować.
wzdłuż jego krawędzi. Tę bryłę barw można poddać
nieliniowemu przekształceniu, w wyniku którego powstaje stożek. Czasem
też przedstawia się tę bryłę jako ostrosłup sześciokątny, być może
dlatego, że łatwiej jest go narysować.
Wierzchołek stożka ma współrzędną ![]() i reprezentuje barwę czarną
(
i reprezentuje barwę czarną
(![]() ). Współrzędne
). Współrzędne ![]() i
i ![]() są w tym punkcie nieokreślone.
są w tym punkcie nieokreślone.
Środek podstawy stożka ma współrzędne ![]() ,
, ![]() i reprezentuje
barwę białą. Punkty na osi stożka reprezentują różne poziomy
szarości; z wyjątkiem wierzchołka stożka współrzędna
i reprezentuje
barwę białą. Punkty na osi stożka reprezentują różne poziomy
szarości; z wyjątkiem wierzchołka stożka współrzędna ![]() jest równa
jest równa
![]() , a
, a ![]() jest nieokreślona. Oddalając się od osi stożka zwiększamy
nasycenie
jest nieokreślona. Oddalając się od osi stożka zwiększamy
nasycenie ![]() do maksymalnej wartości
do maksymalnej wartości ![]() na powierzchni bocznej stożka.
Współrzędna
na powierzchni bocznej stożka.
Współrzędna ![]() odpowiada kątowi obrotu wokół osi stożka.
Rysunek 12.7 przedstawia rozmieszczenie barw o poszczególnych
odcieniach.
odpowiada kątowi obrotu wokół osi stożka.
Rysunek 12.7 przedstawia rozmieszczenie barw o poszczególnych
odcieniach.
Do przejścia między układami ![]() i
i ![]() służą poniższe procedury,
napisane przy założeniu, że wszystkie współrzędne przebiegają
przedział
służą poniższe procedury,
napisane przy założeniu, że wszystkie współrzędne przebiegają
przedział ![]() . Czasem współrzędną
. Czasem współrzędną ![]() podaje się w stopniach, od
podaje się w stopniach, od ![]() do
do ![]() .
.
| procedure RGBtoHSV ( |
| begin |
| max := |
| min := |
| delta := max-min; |
| |
| if max |
| if |
| if |
| else if |
| else |
| if |
| |
| end |
| end {RGBtoHSV}; |
| procedure HSVtoRGB ( |
| begin |
| if |
| else begin |
| if |
| |
| a := |
| 1: begin |
| 2: begin |
| 3: begin |
| 4: begin |
| 5: begin |
| end |
| end |
| end {HSVtoRGB}; |
Współrzędna ![]() w układzie
w układzie ![]() jest taka sama dla np. najjaśniejszej
barwy niebieskiej, jak i dla białej. Ponieważ w tym drugim przypadku barwa
jest związana z większą mocą światła, więc bardziej intuicyjny
może wydawać się układ
jest taka sama dla np. najjaśniejszej
barwy niebieskiej, jak i dla białej. Ponieważ w tym drugim przypadku barwa
jest związana z większą mocą światła, więc bardziej intuicyjny
może wydawać się układ ![]() , w którym bryła barw składa się
z dwóch stożków zetkniętych podstawami. Współrzędna
, w którym bryła barw składa się
z dwóch stożków zetkniętych podstawami. Współrzędna ![]() (ang. Light), która zastępuje współrzędną
(ang. Light), która zastępuje współrzędną ![]() w tym układzie, dla
światła białego ma wartość
w tym układzie, dla
światła białego ma wartość ![]() , natomiast barwy ,,czyste”
o maksymalnym nasyceniu (które w bryle barw
, natomiast barwy ,,czyste”
o maksymalnym nasyceniu (które w bryle barw ![]() leżą na brzegu podstawy
stożka) mają współrzędną
leżą na brzegu podstawy
stożka) mają współrzędną ![]() . Wprawdzie światło żółte (
. Wprawdzie światło żółte (![]() ,
,
![]() ) wydaje się znacznie jaśniejsze niż np. niebieskie (
) wydaje się znacznie jaśniejsze niż np. niebieskie (![]() ,
,
![]() ; luminancja światła żółtego jest równa
; luminancja światła żółtego jest równa ![]() , a niebieskiego
, a niebieskiego
![]() , czyli jest
, czyli jest ![]() razy mniejsza), ale takie rozwiązanie okazało się
użyteczne.
razy mniejsza), ale takie rozwiązanie okazało się
użyteczne.
Wybór układu współrzędnych i związanej z nim bryły barw jest ważny
nie tylko ze względu na wygodę wybierania pojedynczych punktów (tj. barw). Znacznie istotniejsze jest mieszanie barw oraz
interpolacja między wskazanymi punktami.
Mieszanie barw podczas filtrowania (zmiany rozdzielczości,
antyaliasing) i interpolacja w cieniowaniu Gourauda najczęściej
wiążą się z addytywnymi układami współrzędnych, natomiast
w interakcyjnym dobieraniu barw często celem jest otrzymanie barw
reprezentowanych przez punkty wskazanego odcinka. Zauważmy, że
interpolacja w bryle barw ![]() polega na interpolacji współrzędnych,
natomiast interpolacja w bryłach
polega na interpolacji współrzędnych,
natomiast interpolacja w bryłach ![]() i
i ![]() wymaga przejścia do
pomocniczego układu współrzędnych kartezjańskich i interpolacji tych
współrzędnych.
wymaga przejścia do
pomocniczego układu współrzędnych kartezjańskich i interpolacji tych
współrzędnych.