Zagadnienia
- 13.1 Wprowadzenie
- 13.2 Przykład wstępny
- 13.3 Operatory PostScriptu
- 13.4 Napisy i tworzenie obrazu tekstu
- 13.5 Słowniki
- 13.6 Stosy interpretera
- 13.7 Operatory konwersji
- 13.8 Przekształcenia afiniczne
- 13.9 Operacje na tablicach
- 13.10 Obrazy rastrowe
- 13.11 Programowanie L-systemów
- 13.12 PostScript obudowany
13. Język PostScript
13.1. Wprowadzenie
Język PostScript został opracowany przez firmę Adobe Systems Inc. w 1985r. Jest to tzw. język opisu strony; plik postscriptowy jest programem, który jest interpretowany przez drukarkę lub inne urządzenie, w celu utworzenia obrazu np. do wydrukowania. Dodatkowo, jest to prawdziwy język programowania (nawet dosyć ,,wysokopoziomowy”), w którym można pisać programy wykonujące skomplikowane obliczenia. Możliwości graficzne można wtedy zignorować lub wykorzystać do wyprowadzenia wyników.
Podstawowa zasada systemu grafiki związanego z językiem PostScript to niezależność opisu strony od urządzenia, które ma utworzyć obraz; wiadomo, że jest to urządzenie rastrowe, ale można i warto używać PostScriptu w oderwaniu od sprzętu; interpreter języka w dowolnym urządzeniu ma za zadanie przedstawić obraz o najlepszej jakości osiągalnej z tym urządzeniem.
Praktyczny przykład tej filozofii: piszemy g setgray, gdzie g
jest liczbą rzeczywistą z przedziału ![]() . Polecenie to ustawia poziom
szarości (
. Polecenie to ustawia poziom
szarości (![]() to kolor czarny,
to kolor czarny, ![]() — biały). Rozwiązanie, w którym
poziom szarości byłby określany przez podanie liczby całkowitej
z przedziału od
— biały). Rozwiązanie, w którym
poziom szarości byłby określany przez podanie liczby całkowitej
z przedziału od ![]() do
do ![]() nosiłoby piętno zależności sprzętowej
(prawdopodobnie od liczby bitów w rejestrach przetwornika
cyfrowo-analogowego sterownika graficznego). Tymczasem dzięki możliwości
podania liczby rzeczywistej
nosiłoby piętno zależności sprzętowej
(prawdopodobnie od liczby bitów w rejestrach przetwornika
cyfrowo-analogowego sterownika graficznego). Tymczasem dzięki możliwości
podania liczby rzeczywistej
-
nie ma ograniczenia tylko do
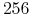 poziomów szarości (istnieją,
co prawda rzadko spotykane, sterowniki z dziesięcio- lub
dwunastobitowymi przetwornikami, więc to rozwiązanie umożliwia pełne
wykorzystanie ich możliwości),
poziomów szarości (istnieją,
co prawda rzadko spotykane, sterowniki z dziesięcio- lub
dwunastobitowymi przetwornikami, więc to rozwiązanie umożliwia pełne
wykorzystanie ich możliwości), -
nawet jeśli jasność jest ostatecznie przeliczana na liczbę całkowitą od
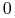 do
do 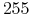 (która będzie przypisana pikselom), może
to być przekształcenie nieliniowe, dopasowane do specyfiki urządzenia
(inne dla drukarki, inne dla monitora).
(która będzie przypisana pikselom), może
to być przekształcenie nieliniowe, dopasowane do specyfiki urządzenia
(inne dla drukarki, inne dla monitora).
Można pisać programy zależne od docelowego urządzenia, warto jednak robić to tylko wtedy, gdy domyślne ustawienie tego urządzenia nie pasuje do specyfiki zastosowania (ale zdarza się to bardzo, bardzo rzadko).
Program GhostScript jest interpreterem języka PostScript, opracowanym przez firmę Aladdin Software. Może on się przydać jako przeglądarka ekranowa, albo sterownik drukarki nie-postscriptowej, który czyni z niej drukarkę postscriptową. W odróżnieniu od większości produktów firmy Adobe, jest dostępny za darmo.
W ostatnim czasie PostScript traci nieco na popularności na rzecz języka PDF (ang. portable document format), też opracowanego przez firmę Adobe. Pliki PDF są binarne (w związku z czym zajmują mniej miejsca) i pozwalają na tworzenie hipertekstu, co przydaje się w pracy z dokumentami elektronicznymi. Do oglądania plików PDF można użyć programu Adobe Acrobat Reader (jest za darmo), ale również GhostScriptu.
Ostatnia sprawa — nazwa. Wzięła się ona od notacji przyrostkowej (ang. postfix), czyli odwrotnej notacji polskiej Łukasiewicza. Notacja ta pozwala na beznawiasowy zapis wyrażeń arytmetycznych. Interpreter PostScriptu jest maszyną stosową której zadaniem jest przetwarzanie kolejnych symboli takich wyrażeń.
13.2. Przykład wstępny
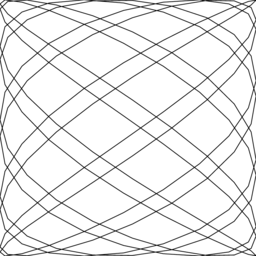
Podany niżej program tworzy pokazany obrazek.
1: %!
2: /nx 10 def
3: /ny 7 def
4: /phi 20 def
5: /size 100 def
6: /transx 20 def
7: /transy 150 def
8: /steps 200 def
9: /cpoint {
10: $\mbox{ \ }$ steps div 360 mul dup
11: $\mbox{ \ }$ phi add nx mul sin 1 add size mul transx add
12: $\mbox{ \ }$ exch
13: $\mbox{ \ }$ ny mul cos 1 add size mul transy add
14: } def
15: newpath
16: 0 cpoint moveto
17: 1 1 steps 1 sub { cpoint lineto } for
18: closepath
19: stroke
20: showpage
Powyższy program służy do narysowania łamanej przybliżajęcej pewną krzywą Lissajous; zmieniając stałe w programie można otrzymywać różne krzywe. Liczby z dwukropkami są numerami linii i nie należy ich pisać w pliku postscriptowym.
Znak komentarz — zaczynając od niego do końca linii wszystkie znaki są
ignorowane przez interpreter. Ludzie komentarze w programach powinni pisać
i czytać. Dwa pierwsze znaki w pliku, \lstPSplik postscriptowy. Bez nich próba wydrukowania zakończyłaby się
otrzymaniem tekstu pliku, zamiast odpowiedniego obrazka.
W kolejnych liniach jest ciąg symboli; część z nich to symbole literalne, a pozostałe są wykonywalne. Interpreter wstawia na stos symbole literalne, natomiast przetwarzanie symbolu wykonywalnego polega na wykonaniu odpowiedniej procedury. Procedura ta może mieć pewną liczbę parametrów — to są obiekty obecne na stosie. Procedura może zdjąć ze stosu pewną liczbę obiektów i wstawić inne.
Na przykład, w linii 2 napis nx to jest symbol literalny,
który jest nazwą (w terminologii PostScriptu — kluczem); następnie mamy
symbol literalny 10, który reprezentuje liczbę całkowitą. Symbol
wykonywalny def powoduje wywołanie procedury przypisania, która
spodziewa się znaleźć na stosie dwa parametry: nazwę i obiekt, który ma
być skojarzony z nazwą. W Pascalu to samo zapisuje się w postaci
nx := 10;.
W liniach 9-14 mamy tekst procedury, która, za pomocą operatora
def (w linii 14) będzie przypisana nazwie cpoint.
Umieszczenie na stosie symbolu { powoduje, że kolejne symbole
będą traktowane jak literalne, aż do pojawienia się (do pary) klamry
zamykającej }. Jest ona symbolem wykonywalnym i powoduje utworzenie
obiektu, który jest procedurą. Obiekt ten jest umieszczony na stosie
i operator def w linii 14 znowu znajduje dwa parametry zamiast
zdjętych ze stosu symboli między nawiasami klamrowymi: nazwę
cpoint i procedurę, która zostaje przypisana tej nazwie.
Linia 15: operator (wykonywalny; nazwy wykonywalne nie mają znaku
/ na początku) newpath zapoczątkowuje nową tzw. ścieżkę; wyznaczy ona w tym przypadku krzywą do narysowania (ale
może też wyznaczyć brzeg obszaru do zamalowania, albo brzeg obszaru, poza
którym malowanie będzie zabronione).
Zbadajmy teraz, co robi procedura cpoint. Znajduje ona na stosie ![]() parametr, który powinien być liczbą z przedziału
parametr, który powinien być liczbą z przedziału 0 ..\ steps-1.
Oznaczmy go literą ![]() ; procedura
; procedura cpoint ma obliczyć
i zostawić na stosie liczby ![]() i
i ![]() . W linii 10 mamy kolejno:
dzielenie
. W linii 10 mamy kolejno:
dzielenie ![]() przez
przez steps (operator div), mnożenie wyniku
przez ![]() (operator
(operator mul) i wstawienie na stos dodatkowej kopii tego
ostatniego wyniku (operator dup). Dalej — dodanie phi
(add), mnożenie przez nx, obliczenie sinusa (operator sin,
kąt jest podawany w stopniach) itd. Po wykonaniu ostatniego add
w linii 11 mamy wartość ![]() na wierzchołku stosu.
na wierzchołku stosu.
Operator exch zamienia miejscami ![]() z obiektem ,,pod
spodem”, po czym (w linii 13) następuje obliczenie
z obiektem ,,pod
spodem”, po czym (w linii 13) następuje obliczenie ![]() .
.
W linii 16 mamy przykład wywołania procedury: 0 (umieszczone
na stosie) jest parametrem procedury cpoint, po wykonaniu której na
stosie są ![]() argumenty
argumenty ![]() i
i ![]() operatora
operatora moveto. Umieszcza on
bieżącą pozycję (którą można sobie wyobrażać jako coś w rodzaju
pisaka) w punkcie ![]() ; ścieżka zaczyna się w tym punkcie, a parametry
operatora
; ścieżka zaczyna się w tym punkcie, a parametry
operatora moveto zostają usunięte ze stosu.
Kolejne ![]() (tj.
(tj. steps-1) punktów — wierzchołków łamanej,
która ma być ścieżką, jest otrzymywane za pomocą operatora for,
który realizuje pętlę. Pierwsze trzy jego parametry to wartość
początkowa zmiennej sterującej (coś jak i w Pascalowym
for i := 1 to steps-1 do …)
oraz przyrost i wartość końcową. Mogą to być liczby rzeczywiste.
Czwarty argument to
procedura (utworzona za pomocą klamer); operator for wywoła ją
odpowiednią liczbą razy, za każdym razem wstawiając uprzednio na stos
wartość zmiennej sterującej. W naszym przykładzie będzie ona parametrem
procedury cpoint. Operator lineto wydłuża ścieżkę do
punktu o współrzędnych ![]() ,
, ![]() zdjętych ze stosu (coś jakby przesuwał
pisak). Zauważmy, że procedura wywoływana przez
zdjętych ze stosu (coś jakby przesuwał
pisak). Zauważmy, że procedura wywoływana przez for w końcowym
efekcie czyści stos ze zmiennej sterującej (i powinna to robić).
Operator closepath łączy koniec ścieżki z jej początkiem.
Operator stroke wykonuje rysowanie łamanej. Nie bierze on
argumentów ze stosu, ale przed jego wywołaniem musi być przygotowana
stosowna ścieżka. Operator showpage powoduje wydrukowanie strony
i przygotowanie interpretera do rysowania na następnej.
13.3. Operatory PostScriptu (wybrane dość arbitralnie)
Język PostScript zawiera wszystkie operatory arytmetyczne, logiczne i inne, jakich można się spodziewać w języku programowania. Operatory te są realizowane przez procedury, które pobierają argumenty ze stosu i pozostawiają na nim wyniki.
Poniższa lista zawiera prawie wszystkie operatory udostępniane przez interpreter, które przydają się w codziennej pracy z PostScriptem. Opis pozostałych można znaleźć w licznych podręcznikach poświęconych wyłącznie temu językowi i w dokumentacji firmowej, której przepisywanie nie byłoby wskazane.
Zgodnie z przyjętym zwyczajem, który jest bardzo wygodny, operator przedstawia się w ten sposób, że przed nim są wymienione argumenty (w kolejności wstawiania na stos), a po nim argumenty, które dany operator na stosie zostawia.
13.3.1. Operatory arytmetyczne
Litera ![]() oznacza, że argument może być liczbą całkowitą lub
rzeczywistą; litera
oznacza, że argument może być liczbą całkowitą lub
rzeczywistą; litera ![]() oznacza, że dopuszczalna jest tylko liczba
całkowita. Typ wyniku zależy od wykonanej operacji i od typu argumentów,
w sposób zgodny z intuicją.
oznacza, że dopuszczalna jest tylko liczba
całkowita. Typ wyniku zależy od wykonanej operacji i od typu argumentów,
w sposób zgodny z intuicją.
|
|
add |
(suma) | |
|---|---|---|---|
|
|
div |
(iloraz |
|
|
|
idiv |
(część całkowita ilorazu |
|
|
|
mod |
(reszta ilorazu |
|
|
|
mul |
(iloczyn) | |
|
|
sub |
(różnica |
|
abs |
(wartość bezwzględna) | ||
neg |
(zmiana znaku) | ||
ceiling |
(zaokrąglanie w górę) | ||
floor |
(zaokrąglanie w dół) | ||
round |
(zaokrąglenie) | ||
truncate |
(obcięcie) | ||
sqrt |
(pierwiastek kwadratowy) | ||
|
|
atan |
( |
cos |
(kosinus |
||
|---|---|---|---|
sin |
(sinus |
||
|
|
exp |
( |
|
ln |
(logarytm naturalny) | ||
log |
(logarytm dziesiętny) | ||
| — | rand |
(liczba losowa) | |
srand |
— | (inicjalizacja generatora liczb losowych) | |
| — | rrand |
(wartość ziarna generatora l. losowych) |
Generator liczb losowych wytwarza oczywiście liczby pseudolosowe, tj. elementy okresowego ciągu liczb o bardzo długim okresie. Jeśli program
inicjalizuje ziarno generatora (tj. zmienną liczbową, która określa
miejsce kolejnego elementu ciągu, który ma podać), to program może
wygenerować ,,losowy” obrazek, który za każdym razem będzie identyczny.
Liczby generowane przez operator rand są całkowite, z przedziału
od ![]() do
do ![]() .
.
13.3.2. Operacje na stosie argumentów
Ze względu na rolę jaką pełni stos argumentów, operatory obsługujące
ten stos są używane często. Litera ![]() niżej oznacza argument
dowolnego typu.
niżej oznacza argument
dowolnego typu.
pop |
— | (usuwa obiekt ze stosu) | |
|---|---|---|---|
|
|
exch |
(zamienia) | |
dup |
(podwaja) | ||
copy |
(kopiuje |
||
roll |
(przestawia) |
13.3.3. Operatory relacyjne i logiczne
Operatory relacyjne służą do badania warunków i można ich użyć w celu
sterowania przebiegiem obliczeń (warunkowe wykonanie podprogramu,
zakończenie pętli itd.). Operatory logiczne realizują koniunkcję,
alternatywę itp. Te same operatory zastosowane do liczb całkowitych
realizują odpowiednie operacje na poszczególnych bitach argumentów, przy
czym ![]() jest uważane za fałsz, a
jest uważane za fałsz, a ![]() za prawdę.
za prawdę.
Litera ![]() oznacza obiekt boolowski, o możliwych wartościach
oznacza obiekt boolowski, o możliwych wartościach true
lub false. Litera ![]() oznacza napis, porównania napisów są
leksykograficzne.
oznacza napis, porównania napisów są
leksykograficzne.
eq |
(test równości) | |||
ne |
(test nierówności) | |||
ge |
||||
gt |
||||
le |
||||
lt |
||||
and |
||||
or |
||||
xor |
||||
not |
||||
| — | true |
|||
| — | false |
13.3.4. Operatory sterujące
Operatory sterujące służą do warunkowego lub wielokrotnego wykonywania
różnych części programu. Realizują one pełny repertuar ,,instrukcji
strukturalnych”, które umożliwiają sterowanie przebiegiem programu,
wykonywanie obliczeń iteracyjnych itd. Zapis tych konstrukcji jest
oczywiście przyrostkowy, w polskiej notacji odwrotnej.
Napis proc oznacza procedurę, która jest przez podane niżej
operatory wykonywana w określonych warunkach.
proc
|
if |
— | (np. 1 2 eq { … } if) |
|---|---|---|---|
procproc |
ifelse |
— | |
proc
|
for |
— | ( |
| końcową zmiennej sterującej pętli) | |||
proc
|
repeat |
— | (pętla powtarzana |
proc |
loop |
— | (pętla ,,bez końca”) |
| — | exit |
— | (wyjście z pętli) |
| — | quit |
— | (wyjście z interpretera) |
Procedura będąca argumentem operatora if jest wykonywana wtedy, gdy
warunek ![]() jest prawdziwy. Operator
jest prawdziwy. Operator ifelse wykonuje procedurę
proc${}_1$ jeśli ![]() albo
albo proc${}_2$ w przeciwnym razie.
Operator for zdejmuje ze stosu swoje cztery argumenty, a następnie
wykonuje procedurę proc w pętli; za każdym
razem przed wywołaniem procedury wstawia na stos wartość zmiennej
sterującej; jej wartość zmienia się od ![]() z krokiem
z krokiem ![]() ; koniec
pętli następuje jeśli wartość zmiennej sterującej jest większa niż
; koniec
pętli następuje jeśli wartość zmiennej sterującej jest większa niż
![]() (jeśli krok jest dodatni) albo jeśli jest mniejsza niż
(jeśli krok jest dodatni) albo jeśli jest mniejsza niż ![]() (jeśli krok jest ujemny). Procedura powinna (ale nie musi) usunąć ze
stosu argumentów wartość zmiennej sterującej.
(jeśli krok jest ujemny). Procedura powinna (ale nie musi) usunąć ze
stosu argumentów wartość zmiennej sterującej.
Operator repeat zdejmuje ze stosu swoje dwa argumenty, a następnie
wykonuje procedurę proc ![]() razy. Operator
razy. Operator loop wykonuje
procedurę wielokrotnie; zakończenie tej iteracji może nastąpić tylko
wskutek wykonania operacji exit albo quit; inne pętle też
mogą być przerwane w ten sposób. Operator quit kończy w ogóle
działanie interpretera.
13.3.5. Operatory konstrukcji ścieżki
Dotychczas opisane operatory odpowiadają za konstrukcje dostępne w dowolnym języku programowania. Obecnie pora na grafikę; większość procedur rysowania wiąże się z tworzeniem i przetwarzaniem ścieżek, które są w ogólności łamanymi krzywoliniowymi.
| — | newpath |
— | (inicjalizacja pustej ścieżki) |
|---|---|---|---|
|
|
moveto |
— | (ustawienie punktu początkowego) |
|
|
rmoveto |
— | (ustawienie punktu początkowego |
| względem bieżącej pozycji) | |||
|
|
lineto |
— | (przedłużenie ścieżki o odcinek) |
|
|
rlineto |
— | (przedłużenie o odcinek o końcu |
| określonym względem bieżącej pozycji) | |||
|
|
arc |
— | (przedłużenie o łuk okręgu) |
|
|
curveto |
— | (krzywa Béziera trzeciego stopnia) |
| — | closepath |
— | (zamknięcie ścieżki) |
| — | currentpoint |
|
(zapisanie na stosie współrzędnych bieżącej pozycji) |
Operatory konstrukcji ścieżki służą do określania krzywych złożonych z odcinków, łuków okręgów i krzywych Béziera. Ścieżka może następnie być narysowana jako linia, może być też wypełniona lub posłużyć do obcinania (podczas rysowania interpreter nie zmienia pikseli poza obszarem, którego brzegiem jest aktualna ścieżka obcinania).
13.3.6. Operatory rysowania
Operatory rysowania to te, których interpretacja powoduje przypisanie
pikselom obrazu wartości. Operatory te (poza erasepage
i show) wymagają wcześniejszego przygotowania ścieżki.
Operator show tworzy ścieżkę opisującą odpowiednie litery,
a następnie wypełnia ją, wywołując fill.
| — | erasepage |
— | (czyszczenie strony) |
|---|---|---|---|
| — | fill |
— | (wypełnianie ścieżki) |
| — | eofill |
— | (wypełnianie ścieżki z parzystością) |
| — | stroke |
— | (rysowanie ścieżki jako linii) |
show |
— | (rysowanie liter napisu) |
13.3.7. Operatory związane ze stanem grafiki
Stan grafiki to struktura danych zawierająca informacje takie jak bieżący kolor, grubość linii, wzorzec linii przerywanych i wiele innych. Poniżej sa wymienione tylko najważniejsze operatory związane ze stanem grafiki.
setlinewidth |
— | (ustawianie grubości kreski) | |
|---|---|---|---|
setgray |
— | (ustawianie poziomu szarości) | |
|
|
setrgbcolor |
— | (ustawianie koloru) |
| — | gsave |
— | (zachowanie stanu grafiki) |
| — | grestore |
— | (przywrócenie stanu grafiki) |
13.4. Napisy i tworzenie obrazu tekstu
Jednym z najważniejszych zastosowań języka PostScript jest tworzenie obrazów tekstu; wiele wydrukowanych stron zawiera tylko tekst. Aby otrzymać obraz tekstu należy utworzyć odpowiednie napisy (literały napisowe), rozmieścić je na stronie (tym najczęściej zajmują się systemy składu), wybrać odpowiednie kroje i wielkości czcionek i spowodowć utworzenie obrazów tych czcionek.
Literał napisowy jest to ciąg znaków, umieszczony w nawiasach
okrągłych, np. (napis). Może on zawierać dowolne, połączone
w pary nawiasy okrągłe, które są wtedy przetwarzane bez problemów. Jeśli
trzeba narysować nawias bez pary, pisze się \( albo
\). Inne zastosowania znaku \ to opisywanie
znaków specjalnych, trudno dostępnych lub niedostępnych w kodzie ASCII.
\n |
— | znak końca linii (LF, ASCII 10), |
|---|---|---|
\r |
— | cofnięcie karetki (CR, ASCII 13), |
\t |
— | tabulator, |
\b |
— | cofnięcie, |
\f |
— | wysuw strony, |
\\ |
— | znak ,,\”, |
\ddd |
— | trzy cyfry ósemkowe, mogą określać dowolny znak |
od \000${}_8$ do \377${}_8$. |
Napis może być podany w kilku liniach i wtedy zawiera znaki końca
linii, chyba że ostatni znak w linii to \ (pojedynczy znak
\ jest przy tym ignorowany). Dla porządku wspomnę, że są
jeszcze inne sposoby zapisywania napisów; ciąg (o parzystej długości)
cyfr szesnastkowych w nawiasach <> (np. <1c3F>) jest często
stosowany do reprezentowania obrazów rastrowych (kolejne dwie cyfry dają kod
szesnastkowy kolejnego bajtu). Jest jeszcze inny sposób, który pozwala
,,pakować” dane (![]() znaki napisu zakodowane w pięciu znakach ,,
drukowalnych”), ale to zostawmy.
znaki napisu zakodowane w pięciu znakach ,,
drukowalnych”), ale to zostawmy.
Aby wykonać napis na tworzonej stronie, trzeba najpierw wybrać krój i wielkość pisma. Przykład:
/Times-Roman findfont 32 scalefont setfont 100 100 moveto (napis) show
Nazwa literalna /Times-Roman oznacza krój pisma o nazwie Times New
Roman. Jest to antykwa szeryfowa dwuelementowa, będąca dwudziestowieczną
wersją tzw. antykwy renesansowej. Została ona zaprojektowana
w 1931r. dla dziennika The Times przez zespół pracujący pod kierunkiem
Stanleya Morisona. Jej cecha charakterystyczna to wąskie litery,
umożliwiające zmieszczenie dużej ilości tekstu na stronie.
Inne kroje pisma dostępne zawsze w PostScripcie, to np. /Palatino
(krój Palatino, zaprojektował go Hermann Zapf w 1948 r.),
/Helvetica (Helvetica, antykwa bezszeryfowa jednoelementowa,
Max Miedinger, 1956 r.),
/Courier (Courier, krój pisma ,,maszynowego”, w którym każdy znak
ma tę samą szerokość). Istnieją wersje pogrubione (np. /Times-Bold)
i pochyłe (kursywy, np. /Times-Italic, /Times-BoldItalic),
a także zestawy znaków specjalnych (/Symbol i /ZapfDingbats).
Ponadto istnieją tysiące krojów dostępnych za darmo i (zwłaszcza) komercyjnych,
którymi można składać teksty i opisywać rysunki.
Jednak dodatkowe zestawy znaków trzeba albo specjalnie doinstalować,
albo umieścić w programie PostScriptowym (zwykle na początku).
Operator findfont wyszukuje krój o podanej nazwie
i umieszcza na stosie obiekt (dokładniej: słownik, o słownikach będzie
dalej) reprezentujący ten krój.
Operator scalefont skaluje czcionki w podanej proporcji. Domyślnie
mają one wysokość ![]() punktu (
punktu (![]() cala), czyli bez lupy są nieczytelne.
Dokładniej — jest to ,,wysokość projektowa”, mają ją na
przykład znaki nawiasów. Obiekt reprezentujący zestaw przeskalowanych
znaków pozostaje na stosie, operator
cala), czyli bez lupy są nieczytelne.
Dokładniej — jest to ,,wysokość projektowa”, mają ją na
przykład znaki nawiasów. Obiekt reprezentujący zestaw przeskalowanych
znaków pozostaje na stosie, operator setfont zdejmuje go ze stosu
i ustawia pisanie tymi znakami w bieżącym stanie grafiki.
Polecenie 100 100 moveto w przykładzie ustawia początek napisu,
który jest następnie malowany przez operator show.
Nieco większy przykład:
%!
shadeshow {
/s exch def
/y exch def
/x exch def
/g 1 def
40 {
/g g 0.025 sub dup setgray def
x y moveto
s show
/x x 0.5 add def
/y y 0.5 sub def
} repeat
1 setgray
x y moveto
s show
} def
/Times-Roman findfont 32 scalefont setfont
100 200 (napis) shadeshow
showpage
Procedura shadeshow w przykładzie otrzymuje za pośrednictwem stosu
![]() parametry: napis i współrzędne jego początku. Przykład pokazuje,
jak zdjąć je ze stosu, przypisując ich wartości nazwanym zmiennym.
Ponieważ wszystkie pozostałe elementy były podane już wcześniej,
proponuję ćwiczenie, polegające na takim przerobieniu
przykładu, aby zamiast operatora
parametry: napis i współrzędne jego początku. Przykład pokazuje,
jak zdjąć je ze stosu, przypisując ich wartości nazwanym zmiennym.
Ponieważ wszystkie pozostałe elementy były podane już wcześniej,
proponuję ćwiczenie, polegające na takim przerobieniu
przykładu, aby zamiast operatora repeat był użyty operator
for, ze zmienną sterującą odpowiadającą poziomowi szarości (zamiast
zmiennej g).
Dygresja na temat polskich liter: problem jest zwykle dosyć trudny, ale nie beznadziejny. Jego rozwiązanie zależy od konkretnego zestawu znaków i sposobu ich kodowania. W standardowym kodowaniu (Adobe Standard Encoding) mamy znaki:
\350 |
— | Ł, | |
|---|---|---|---|
\370 |
— | ł, | |
\302 |
— | ́ | (akcent do ć, ń, ś, ó, ź, Ć, Ń, Ś, Ó, Ź), |
\316 |
— | (ogonek do ą, ę, Ą, Ę), | |
\307 |
— | (kropka do ż i Ż). |
Ponieważ zestawy znaków można przekodowywać (tj. inaczej wiązać znaki z kodami, tj. wartościami bajtów w napisie), więc znaki te mogą być dostępne pod innymi kodami, albo niedostępne.
Położenie kropki do ,,ż” i kreski do ,,ć” jest odpowiednie dla małych liter; dla wielkich liter znaki diakrytyczne muszą być odpowiednio podniesione. Aby wypisać cały alfabet, możemy użyć programu
/Times-Roman findfont 30 scalefont setfont 100 100 moveto (P) show currentpoint (\302) show moveto (ojd) show currentpoint (\302) show moveto (z) show currentpoint (\307) show moveto (ze, ki) show currentpoint (\302) show moveto (n t) currentpoint (\316) show moveto (e chmurno) show currentpoint (\302) show moveto (s) show currentpoint (\302) moveto (c w g\370) show currentpoint (\316) show moveto (ab flaszy!) show
Procedura currentpoint zapisuje na stosie bieżącą pozycję przed narysowaniem
znaku diakrytycznego, a procedura moveto ją przywraca, dzięki czemu
np. litera ,,o” jest rysowana na właściwym miejscu, pod kreską, tworząc ,,ó”.
Wracając do poprzedniego przykładu; po ostatniej linijce procedury (s show)
dopiszmy jeszcze
0.5 setlinewidth 0 setgray newpath x y moveto s false charpath stroke
Operator charpath otrzymuje dwa parametry. Pierwszy to napis, a drugi parametr
jest boolowski, false albo true. Wynikiem działania operatora
charpath jest utworzenie zarysu liter i dołączenie ich do
bieżącej ścieżki. Ścieżkę tę w przykładzie wykreślił operator
stroke. Drugi parametr powinien mieć wartość false wtedy,
gdy ścieżkę chcemy wykreślić (tak jak w tym przykładzie). Wartość
true przygotowuje ścieżkę do wypełniania/obcinania (wersja
GhostScriptu, z którą sprawdzałem te przykłady, nie daje widocznych
różnic, ale dla innych interpreterów języka PostScript może to mieć
istotne znaczenie).
Zmieńmy teraz ostatnią linię procedury na
newpath x y moveto s true charpath clip
a po wywołaniu procedury charpath (przed showpage) dopiszmy
300 -5 150 {
newpath 0 exch moveto 500 0 rlineto stroke
} for
Jak widać, tylko kreski wewnątrz liter są narysowane; cokolwiek innego byśmy chcieli dalej narysować, ukaże się tylko część wspólna tego czegoś i liter napisu.
Częścią stanu grafiki jest tzw. ścieżka obcinania; początkowo
jest ona brzegiem strony. Można utworzyć dowolną zamkniętą ścieżkę
i za pomocą operatora clip ograniczyć rysowanie do obszaru, który
jest częścią wspólną obszaru ograniczonego poprzednio ustawionymi
ścieżkami i obszaru, którego brzeg stanowi ścieżka właśnie utworzona.
W ten sposób można rysowanie uniemożliwić całkowicie; jeśli chcemy
przywrócić możliwość rysowania poza obszarem ograniczonym dawną
ścieżką, to powinniśmy przed wywołaniem operatora clip
napisać gsave; późniejsze wywołanie operatora grestore
przywróci stan grafiki (cały) sprzed wywołania gsave, łącznie ze
ścieżką obcinania.
13.5. Słowniki
Zmienne w procedurze nie są lokalne; możemy mieć lokalne zmienne, tworząc słowniki. Przykład:
%!
/tree {
4 dict begin
/a exch def
/l exch def
/y exch def
/x exch def
l 10 ge {
newpath
x y moveto
a cos l mul a sin l mul rlineto
currentpoint
stroke
l 0.8 mul 3 copy
a 15 add tree
a 15 sub tree
} if
end
} def
200 100 70 90 tree
showpage
Mamy tu rekurencyjną procedurę, która ma lokalne zmienne (x,
y, l, a) i przypisuje im wartości parametrów zdjętych
ze stosu. Nie można ich przypisywać zmiennym globalnym, bo rekurencyjne
wywołania zniszczą ich wartości. Dlatego procedura tworzy słownik, czyli
wykaz par nazwa/skojarzony z nią obiekt. Słownik ten zostaje umieszczony
na stosie słowników; ma on pojemność ![]() obiektów i to w nim operator
obiektów i to w nim operator
def wywołany w procedurze tworzy klucze i przypisuje im znaczenie.
Operator dict tworzy obiekt — słownik, którego pojemność jest
określona za pomocą parametru, i umieszcza go na stosie argumentów.
Operator begin zdejmuje obiekt ze stosu argumentów; powinien to być
słownik. Słownik ten zostaje umieszczony na stosie słowników i otwarty
do czytania i pisania. Operator end usuwa go ze stosu słowników.
Można utworzyć dowolnie dużo słowników, ponazywać je i trzymać w nich różne zestawy informacji. Na przykład, program
/slowik 20 dict def
tworzy słownik o pojemności ![]() miejsc i przypisuje go nazwie
miejsc i przypisuje go nazwie
slowik. Później można napisać
slowik begin
co spowoduje umieszczenie tego słownika na stosie słowników
i możliwość czytania i pisania w nim. Operator def zmienia
zawartość słownika na szczycie stosu; jeśli natomiast w programie pojawi
się nazwa wykonywalna, to słowniki są przeszukiwane kolejno, zaczynając
od wierzchołka stosu, aż do znalezienia obiektu skojarzonego z tą nazwą.
Na początku działania interpretera na stosie są
systemdict |
—
słownik tylko do czytania, zawiera nazwy wszystkich operatorów wbudowanych w interpreter PostScriptu i standardowe fonty, |
|---|---|
globaldict |
—
słownik do czytania/pisania w tzw. globalnej pamięci wirtualnej (nie będziemy w to wnikać), |
userdict |
—
słownik do czytania/pisania w tzw. lokalnej
pamięci wirtualnej; to w nim są tworzone obiekty przez |
Oprócz tego istnieją słowniki opisujące kroje pisma, wzorce tworzenia
półtonów i inne, ale nie są one na stosie — można je tam umieścić,
posługując się nazwami obecnymi w słowniku systemdict.
13.6. Stosy interpretera
Interpreter przetwarza cztery stosy; stos argumentów (na którym są
umieszczane kolejne symbole literalne programu), stos słowników,
opisany w poprzednim punkcie, stos stanów grafiki (obsługiwany za
pomocą operatorów gsave i grestore i stos wywołanych
procedur, w którym przechowuje się adresy powrotne. Wszystkie cztery
stosy działają niezależnie, tj. można wstawiać na każdy z nich
i zdejmować obiekty bez związku z kolejnością działań na pozostałych
stosach.
13.7. Operatory konwersji
cvi |
(konwersja liczby rzeczywistej albo napisu na l. całkowitą) | ||
|---|---|---|---|
cvr |
(konwersja liczby lub napisu na l. rzeczywistą) | ||
|
|
cvs |
(konwersja w układzie dziesiętnym) | |
|
|
cvrs |
(konwersja w układzie o podstawie |
Argument ![]() jest napisem, czyli tablicą znaków, którą trzeba wcześniej
utworzyć. Dla operatora
jest napisem, czyli tablicą znaków, którą trzeba wcześniej
utworzyć. Dla operatora cvi powinien napis ten powinien
składać się z samych cyfr (z ewentualnym znakiem na początku);
dla cvr może zawierać mnożnik, który jest potęgą ![]() ,
np.
,
np. 3.14e-5. Operatory cvs i cvrs wymagają podania
liczby ![]() poddawanej konwersji, podstawy
poddawanej konwersji, podstawy ![]() (np.
(np. ![]() — tylko ten
ostatni) i tablicy, w której mają być umieszczone znaki (głównie cyfry)
napisu reprezentującego liczbę
— tylko ten
ostatni) i tablicy, w której mają być umieszczone znaki (głównie cyfry)
napisu reprezentującego liczbę ![]() . Do utworzenia takiej tablicy służy
operator
. Do utworzenia takiej tablicy służy
operator string, na przykład fragment programu
/temp 12 string def
tworzy napis o długości ![]() znaków. Początkowo otrzymują one wartość
znaków. Początkowo otrzymują one wartość
![]() .
.
Pierwszy argument operatora cvs nie musi być liczbą; jeśli jest to
obiekt reprezentujący wartość boolowską, to cvs utworzy napis
true albo false; jeśli argument jest nazwą operatora, to
otrzymamy napis – nazwę. W pozostałych przypadkach (np. słownik,
tablica, procedura) wystąpi błąd.
13.8. Przekształcenia afiniczne
Współrzędne punktów we wszystkich dotychczasowych przykładach były
podawane w układzie, którego początek pokrywa się z lewym dolnym rogiem
strony, oś ![]() jest pozioma, oś
jest pozioma, oś ![]() — pionowa, a jednostką długości
jest
— pionowa, a jednostką długości
jest ![]() punkt, czyli
punkt, czyli ![]() cala (obecna definicja to
cala (obecna definicja to ![]() cal
cal ![]()
![]() mm,
do roku
mm,
do roku ![]() obowiązywał nieco większy cal, taki że
obowiązywał nieco większy cal, taki że ![]() cm
cm![]() cala).
cala).
Jeśli ktoś chciałby umieścić początek układu w innym punkcie, to może
rysowanie opisać wyłącznie za pomocą komend ,,względnych”, np. rlineto i wtedy wystrczy zmienić tylko punkt startowy. Ale:
-
to załatwia tylko przesunięcia,
-
może być niewygodne,
-
może być niewykonalne, jeśli gotowy obrazek postscriptowy chcemy wkomponować w inny obrazek.
Operator translate otrzymuje dwa parametry, które opisują
współrzędne (w dotychczasowym układzie) początku nowego układu,
który będzie odtąd używany. Kierunki osi i jednostki długości obu
układów są takie same.
Dwuargumentowy operator scale służy do zmiany jednostek długości;
układ współrzędnych, który obowiązuje po jego zastosowaniu ma
ten sam początek i kierunki osi; pierwszy argument określa skalowanie osi
![]() , a drugi
, a drugi ![]() . Rysunek wykonany po poleceniach
. Rysunek wykonany po poleceniach 2 dup scale
jest ![]() razy większy niż byłby bez tego. Podając różne
współczynniki skalowania, np.
razy większy niż byłby bez tego. Podając różne
współczynniki skalowania, np. 2 3 scale, możemy spowodować,
że polecenie rysowania okręgu spowoduje narysowanie elipsy.
Jednoargumentowy operator rotate pozwala rysunek obrócić; argument
określa kąt obrotu w stopniach, w kierunku przeciwnym do zegara. Operatory
scale i rotate mają punkt stały, który jest początkiem
dotychczasowego układu, określonego przez poprzednio wykonane
przekształcenia. To działa tak, że jeśli mamy fragment programu
w PostScripcie, który coś rysuje, to cokolwiek w nim byśmy przekształcali
(z wyjątkiem, o którym później), jeśli poprzedzimy go pewnym
przekształceniem, to odpowiednio przekształcimy ten rysunek w całości.
Dzięki temu program, który umieszcza rysunek postscriptowy na stronie
(w odpowiednim położeniu względem tekstu), może go poprzedzić
przekształceniami, które ustalają odpowiednią wielkość i pozycję.
Dodatkowo, taki program okłada kod opisujący rysunek poleceniami
gsave i grestore; może też ustawić ścieżkę obcinania (aby kod
rysunku nie mógł mazać po tekście), utworzyć nowy słownik dla rysunku
(aby wszystkie skutki działania operatora def w kodzie rysunku
zlikwidować za końcem rysunku)
i w słowniku tym wykonuje polecenie /showpage {} def, dzięki
czemu polecenie showpage w pliku z obrazkiem nie spowoduje
wydrukowania niekompletnej strony.
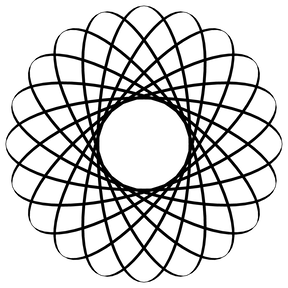
Przykład:
%!
/ell {
10 {
1 3 scale
newpath
0 0 80 0 360 arc stroke
1 1 3 div scale
18 rotate
} repeat
} def
2 setlinewidth
297 421 translate
ell
showpage
Skalowanie zostało wykorzystane do otrzymania elipsy o półosiach
o długościach ![]() i
i ![]() ; po narysowaniu elipsy wracamy do
nieprzeskalowanych jednostek. Grubość linii, którymi
elipsy są
narysowane, zmienia się, co jest spowodowane tym, że operator
; po narysowaniu elipsy wracamy do
nieprzeskalowanych jednostek. Grubość linii, którymi
elipsy są
narysowane, zmienia się, co jest spowodowane tym, że operator
stroke zamienia ścieżkę opisującą elipsę na dwie krzywe, między
którymi jest obszar zamalowywany na czarno. Krzywe te są równoodległe
w bieżącym układzie współrzędnych, o różnych jednostkach długości
osi w tym przypadku.
Pisząc powyższy przykład zrobiłem błąd, który jest wart obejrzenia. Zapisałem procedurę tak:
/ell {
1 3 scale
10 {
newpath
0 0 80 0 360 arc stroke
18 rotate
} repeat
} def
Jaki był skutek i dlaczego? (proszę odpowiedzieć bez pomocy komputera).
Teraz modyfikacja:
%!
/ell {
newpath
10 {
1 3 scale
80 0 moveto
0 0 80 0 360 arc
1 1 3 div scale
18 rotate
} repeat
stroke
} def
2 setlinewidth
297 421 translate
ell
showpage
Linie mają teraz grubość stałą, bo operator scale działa
w układzie, którego jednostki osi mają tę samą długość. Polecam jako
ćwiczenie zastanowienie się, jak narysować takie coś jak na rysunku poniżej.
Zamieńmy w ostatnim przykładzie stroke na fill lub
eofill i obejrzyjmy skutki.
W powyższych przykładach zmiany układu współrzędnych są zrobione
w sposób dość niedołężny. Chodzi o parę 1 3 scale
i 1 1 3 div scale. Po pierwsze, tę samą stałą powtórzyłem w dwóch miejscach,
a po drugie, wskutek błędów zaokrągleń nie przywracamy dokładnie stanu
poprzedniego (w przykładzie na rysunku tego nie widać, ale błędy mogą
wyleźć w poważniejszych zastosowaniach). Nie można w celu przywrócenia
poprzedniego układu użyć pary gsave - grestore, bo to by
zniszczyło konstruowaną ścieżkę. Możliwe jest takie rozwiązanie:
/ell {
newpath
10 {
[ 0 0 0 0 0 0 ] currentmatrix
1 3 scale
80 0 moveto
0 0 80 0 360 arc closepath
setmatrix
18 rotate
} repeat
eofill
} def
Bieżący układ współrzędnych, a właściwie tzw. CTM (ang. current transformation matrix), czyli macierz przekształcenia
używanego w danej chwili do obliczania punktów w układzie urządzenia,
jest reprezentowana w postaci tablicy o ![]() elementach. Macierz ta jest
częścią stanu grafiki. Operator
elementach. Macierz ta jest
częścią stanu grafiki. Operator currentmatrix ma
![]() argument — obiekt, który jest tablicą; operator
ten wpisuje do niej współczynniki bieżącego przekształcenia i zostawia
tablicę na stosie. Operator
argument — obiekt, który jest tablicą; operator
ten wpisuje do niej współczynniki bieżącego przekształcenia i zostawia
tablicę na stosie. Operator setmatrix przypisuje macierzy CTM
współczynniki z tablicy podanej jako argument (w przykładzie —
pozostawionej na stosie przez currentmatrix).
Samą macierz utworzyłem tu w sposób najbardziej ,,jawny” — przez
podanie odpowiedniej liczby współczynników w nawiasach kwadratowych. Ich
wartości w przykładzie są nieistotne, bo currentmatrix zaraz je
zamaże. Można też napisać 6 array albo matrix; pierwszy
z tych operatorów tworzy tablicę o długości określonej przez parametr,
a drugi tablicę o długości ![]() . Operator
. Operator matrix dodatkowo przypisuje
współczynnikom macierzy wartości reprezentujące przekształcenie
tożsamościowe.
Oczywiście, aby odwoływać się do tablicy wielokrotnie, można ją nazwać, mogą być więc takie fragmenty programu, jak
/tab 6 array currentmatrix def
Do celów specjalnych (!) służy
operator initmatrix, który przypisuje CTM jej wartość
początkową, niwecząc w ten sposób skutki wszystkich wcześniejszych
operacji translate, scale, rotate i setmatrix.
Z tego powodu obrazek, który został umieszczony na stronie przez program
do składu, pojawi się zawsze w tym samym miejscu, jeśli na jego początku
jest wywołanie initmatrix.
13.9. Operacje na tablicach
Jak wspomniałem, operator [ zaczyna konstrukcję tablicy, a ]
liczy operatory na stosie, rezerwuje odpowiednie miejsce i przypisuje
obiekty ze stosu elementom tablicy. Zakres indeksów tablicy zaczyna się od
![]() (tak, jak w języku C). Aby ,,wydłubać” element tablicy,
stosujemy operator
(tak, jak w języku C). Aby ,,wydłubać” element tablicy,
stosujemy operator get, np. po wykonaniu kodu [ 10 21 32 ] 1 get
na stosie zostaje 21.
Zamiast tablicy, argumentem operatora get może być napis i wtedy na
stosie zostaje umieszczona liczba całkowita, która jest kodem
odpowiedniego znaku, np. po wykonaniu (abcd) 1 get zostaje liczba
![]() , czyli kod znaku
, czyli kod znaku b.
Pierwszym argumentem get może być też słownik; zamiast indeksu
liczbowego podaje się wtedy nazwę (klucz) obiektu w słowniku, np.
/mykey (napis) def currentdict /mykey get
Po wykonaniu powyższego kodu na stosie zostaje (napis).
Przypisanie wartości elementowi tablicy wykonuje się za pomocą operatora
put; ma on ![]() argumenty: tablicę, indeks i obiekt, który ma być
przypisany. Należy podkreślić, że tablica może zawierać obiekty
różnych typów, np. liczby, napisy, tablice itd. Jeśli zamiast tablicy
pierwszym argumentem
argumenty: tablicę, indeks i obiekt, który ma być
przypisany. Należy podkreślić, że tablica może zawierać obiekty
różnych typów, np. liczby, napisy, tablice itd. Jeśli zamiast tablicy
pierwszym argumentem put jest napis, to trzeci argument, czyli obiekt
przypisywany, musi być liczbą całkowitą; na odpowiedniej pozycji napisu
pojawi się znak, którego kodem jest ta liczba.
Zamiast tablicy lub napisu i indeksu liczbowego, można podać słownik
i klucz, a więc operator put może być użyty do kojarzenia wartości
z kluczami w dowolnym słowniku, niekoniecznie umieszczonym na stosie
słowników.
Są też operatory getinterval i putinterval, które
,,wyjmują” i ,,wkładają” do tablicy lub napisu podciąg wartości:
|
|
getinterval |
||
|---|---|---|---|
|
|
getinterval |
Po wykonaniu operacji, na stosie pozostaje obiekt, który jest ,,
podtablicą” lub ,,podnapisem” o długości ![]() , którego pierwszym
elementem jest obiekt lub znak na
, którego pierwszym
elementem jest obiekt lub znak na ![]() -tej pozycji w pierwszym argumencie.
Uwaga: to nie jest kopia odpowiednich elementów, tylko obiekt, który
wskazuje elementy w podanej tablicy. Aby utworzyć kopię, należy
użyć operatora
-tej pozycji w pierwszym argumencie.
Uwaga: to nie jest kopia odpowiednich elementów, tylko obiekt, który
wskazuje elementy w podanej tablicy. Aby utworzyć kopię, należy
użyć operatora putinterval:
|
|
putinterval |
— | |
|
|
putinterval |
— |
Na przykład:
/s1 (0123456789) def
/s2 (aaaaaaaaaa) def
s2 4
s1 2 4 getinterval % wyciągnij 4 znaki z s1
putinterval % wstaw do s2, od miejsca nr 4
% teraz s2 = (aaaa2345aa)
Wreszcie, istnieje operator forall, który pozwala wykonać pewną
procedurę na wszystkich elementach tablicy, wszystkich znakach napisu, albo
na wszystkich kluczach w słowniku. Pierwszym jego argumentem jest
tablica/napis/słownik, drugim procedura. Jeśli pierwszy argument jest
tablicą, to operator forall przed każdym wywołaniem procedury
wstawia na stos kolejny element. Jeśli to napis, to będą to liczby
całkowite od ![]() do długości napisu
do długości napisu![]() . Jeśli argumentem jest słownik,
to operator wstawia na stos kolejne pary klucz/wartość. W przypadku
słownika kolejność kluczy jest przypadkowa.
. Jeśli argumentem jest słownik,
to operator wstawia na stos kolejne pary klucz/wartość. W przypadku
słownika kolejność kluczy jest przypadkowa.
Jeśli procedura nie usunie obiektów wstawianych na stos, to zostają tam
one, co może być celowe. Wykonanie operatora exit w procedurze
powoduje zakończenie działania jej i operatora forall.
13.10. Obrazy rastrowe
Często zdarza się potrzeba narysowania obrazu rastrowego, dostarczonego z zewnątrz (może to być zeskanowana fotografia lub obraz wygenerowany na przykład przez program śledzenia promieni). Rozdzielczość takiego obrazu na ogół nie ma związku z rozdzielczością rastra urządzenia, dla którego interpreter PostScriptu tworzy obraz. Tworzenie takiego obrazu, oprócz zmiany rozdzielczości obejmuje przekształcanie skali szarości i barw, co tu pominiemy, zastępując to stwierdzeniem, że jest to zwykle robione dobrze.
Do odwzorowania obrazu rastrowego służy operator image, który ma
następujące argumenty:
|
|
image |
— |
Liczby całkowite ![]() i
i ![]() określają wysokość i szerokość obrazu
(w pikselach ,,oryginalnych”). Liczba
określają wysokość i szerokość obrazu
(w pikselach ,,oryginalnych”). Liczba ![]() ma wartość
ma wartość ![]() ,
, ![]() ,
, ![]() ,
, ![]() lub
lub ![]() i określa liczbę bitów na piksel. Macierz
i określa liczbę bitów na piksel. Macierz ![]() określa wymiary
i położenie obrazu na stronie utworzonej przez interpreter PostScriptu;
jeśli reprezentuje ona przekształcenie tożsamościowe, to każdy piksel
obrazu oryginalnego jest (w bieżącym układzie współrzędnych) kwadratem
o boku o długości
określa wymiary
i położenie obrazu na stronie utworzonej przez interpreter PostScriptu;
jeśli reprezentuje ona przekształcenie tożsamościowe, to każdy piksel
obrazu oryginalnego jest (w bieżącym układzie współrzędnych) kwadratem
o boku o długości ![]() punkt. Zadaniem procedury
punkt. Zadaniem procedury ![]() jest dostarczanie
danych (czyli wartości kolejnych pikseli); najczęściej procedura ta czyta
dane z pliku, ale może również generować je na podstawie jakichś
obliczeń (co między innymi umożliwia korzystanie z kompresji danych).
Przykład:
jest dostarczanie
danych (czyli wartości kolejnych pikseli); najczęściej procedura ta czyta
dane z pliku, ale może również generować je na podstawie jakichś
obliczeń (co między innymi umożliwia korzystanie z kompresji danych).
Przykład:
%!
/picstr 1 string def
/displayimage {
/h exch def
/w exch def
w h 8 [ 1 0 0 -1 0 h ]
{ currentfile picstr readhexstring pop }
image
} def
200 100 translate
40 dup scale
6 4 displayimage
00ff44ff88ff
44ffffffff88
88ffffffff44
ccffcc884400
showpage
Współczynniki macierzy ![]() w przykładzie powodują zmianę zwrotu
osi
w przykładzie powodują zmianę zwrotu
osi ![]() (to jest to
(to jest to -1) i odpowiednie przesunięcie (o h) do
góry. Dzięki temu kolejne wiersze danych reprezentują rzędy pikseli
,,od góry do dołu”.
Operator currentfile wstawia na stos obiekt reprezentujący plik
bieżąco przetwarzany przez interpreter. Następnie readhexstring
czyta z niego cyfry szesnastkowe i wpisuje odpowiednie kody (liczby
całkowite od ![]() do
do ![]() ) do bufora, którym jest tu napis
) do bufora, którym jest tu napis picstr.
Napis ten zostaje na stosie (skąd konsumuje go operator image), ale
nad nim jest jeszcze obiekt boolowski (false jeśli wystąpił koniec
pliku), który trzeba usunąć za pomocą pop. Ze względu na
prędkość lepszy byłby dłuższy bufor (np. o długości równej
szerokości obrazka), ale nie jest to aż tak ważne.
Dla obrazów kolorowych mamy operator colorimage; jeden ze sposobów
użycia go jest następujący:
false 3} & \lstPScolorimage+ |
— |
Parametry ![]() ,
, ![]() ,
, ![]() i
i ![]() mają takie samo znaczenie jak dla operatora
mają takie samo znaczenie jak dla operatora
image; argument ![]() jest procedurą dostarczającą dane. Argument
boolowski
jest procedurą dostarczającą dane. Argument
boolowski false oznacza, że jest tylko jedna taka procedura, która
dostarcza wszystkie składowe koloru. Ostatni argument, 3, oznacza, że
składowych tych jest ![]() — czerwona, zielona i niebieska. Wartość
— czerwona, zielona i niebieska. Wartość ![]() oznaczałaby składowe CMYK (ang. Cyan, Magenta, Yellow
i blacK, czyli niebieskozielona, purpurowa, żółta i czarna).
oznaczałaby składowe CMYK (ang. Cyan, Magenta, Yellow
i blacK, czyli niebieskozielona, purpurowa, żółta i czarna).
W języku PostScript poziomu drugiego (ang. Level 2) operator
image jest bardziej rozbudowany i w szczególności może służyć do
odtwarzania obrazów kolorowych.
13.11. Programowanie L-systemów
Systemy Lindenmayera, albo L-systemy są pewnego rodzaju językami formalnymi, czyli zbiorami napisów możliwymi do otrzymania wskutek stosowania określonych reguł. Największe zastosowanie znalazły one w modelowaniu roślin; A. Lindenmayer był biologiem; wspólnie z informatykiem P. Prusinkiewiczem opracował wspomniane reguły właśnie w tym celu. L-systemami zajmiemy się w drugim semestrze bardziej szczegółowo; tymczasem spróbujemy wykorzystać interpreter PostScriptu do symulacji generatora i interpretera L-systemów i obejrzymy trochę obrazków.
Na początek formalności. Bezkontekstowy, deterministyczny L-system (tzw. D![]() L-system) jest trójką obiektów:
L-system) jest trójką obiektów: ![]() , gdzie
, gdzie
-
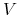 — alfabet (pewien ustalony, skończony zbiór symboli),
— alfabet (pewien ustalony, skończony zbiór symboli), -
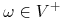 — aksjomat (pewien niepusty napis nad alfabetem
— aksjomat (pewien niepusty napis nad alfabetem
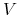 ),
), -
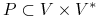 — skończony zbiór tzw. produkcji.
Każdą produkcję można zapisać w postaci
— skończony zbiór tzw. produkcji.
Każdą produkcję można zapisać w postaci
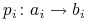 . Symbol
. Symbol 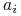 jest tu znakiem
alfabetu
jest tu znakiem
alfabetu 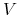 , a
, a 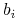 oznacza pewien (być może pusty) napis. Każdemu
symbolowi alfabetu w D
oznacza pewien (być może pusty) napis. Każdemu
symbolowi alfabetu w D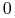 L-systemie odpowiada jedna produkcja, a więc
zbiór produkcji i alfabet są równoliczne.
L-systemie odpowiada jedna produkcja, a więc
zbiór produkcji i alfabet są równoliczne.
Produkcja jest regułą zastępowania symboli w przetwarzanych napisach. Interpretacja L-systemu polega na przetwarzaniu kolejnych napisów; pierwszy z nich to aksjomat; każdy następny napis powstaje z poprzedniego przez zastąpienie każdego symbolu przez ciąg symboli po prawej stronie odpowiedniej produkcji (uwaga: to jest istotna różnica między L-systemami i językami formalnymi Chomsky'ego; obecność w językach Chomsky'ego i brak w L-systemach rozróżnienia symboli tzw. terminalnych i nieterminalnych to różnica nieistotna).
Jeden z najprostszych L-systemów wygląda następująco:
W pierwszych dwóch iteracjach otrzymamy kolejno napisy
Każdy taki napis możemy potraktować jak program, wykonując odpowiednią procedurę dla każdego znaku. Do otrzymania rysunku figury geometrycznej przydaje się tzw. grafika żółwia, nazwana tak, zdaje się, przez twórców skądinąd pożytecznego języka LOGO. Żółw jest obiektem, który w każdej chwili ma określone położenie (punkt na płaszczyźnie, w którym się znajduje) i orientację, czyli kierunek i zwrot drogi, w której się poruszy (chyba, że przed wydaniem polecenia ruchu zmienimy tę orientację). Procedury w PostScripcie, realizujące grafikę żółwia, można napisać w taki sposób:
/TF {
newpath
x y moveto
dist alpha cos mul dup x add /x exch def
dist alpha sin mul dup y add /y exch def
rlineto stroke
} def
/TPlus {
/alpha alpha dalpha add def
} def
/TMinus {
/alpha alpha dalpha sub def
} def
Procedura TF realizuje ruch żółwia od bieżącej pozycji,
o współrzędnych x, y, na odległość dist, w kierunku
określonym przez kąt alpha. Procedury TPlus i TMinus
zmieniają orientację, tj. dodają lub odejmują ustalony przyrost dalpha
do lub od kąta alpha.
Powyższe procedury zwiążemy odpowiednio z symbolami ![]() ,
, ![]() i
i ![]() w napisie otrzymanym w ostatniej iteracji; łatwo to zrobić, pisząc
rekurencyjne procedury
w napisie otrzymanym w ostatniej iteracji; łatwo to zrobić, pisząc
rekurencyjne procedury F, Plus i Minus, które
realizują produkcje, a po dojściu do określonego poziomu rekurencji
sterują żółwiem. Można to zrobić tak:
%!
... % tu wstawiamy procedury TF, TPlus, TMinus
/F {
/iter iter 1 add def
iter itn eq { TF }
{
F Plus F Minus Minus F Plus F
} ifelse
/iter iter 1 sub def
} def
/Plus { TPlus } def
/Minus { TMinus } def
/dist 5 def
/dalpha 60 def
/iter 0 def
/itn 5 def
/x 100 def
/y 500 def
/alpha 0 def
F Minus Minus F Minus Minus F Minus Minus
showpage
Kolejne symbole napisu są reprezentowane przez wywołania procedur na
odpowiednim poziomie rekurencji.
Procedury Plus i Minus opisują produkcje, które zastępują
symbol ![]() lub
lub ![]() nim samym i dlatego mogą od razu wywołać procedury
geometrycznej interpretacji tych symboli, bez rekurencji. Natomiast
w procedurze
nim samym i dlatego mogą od razu wywołać procedury
geometrycznej interpretacji tych symboli, bez rekurencji. Natomiast
w procedurze F poziom rekurencji, przechowywany w zmiennej iter,
decyduje o tym, czy generować symbole kolejnego napisu, czy też dokonać
interpretacji geometrycznej — w tym przypadku ruchu żółwia, który
kreśli. Łatwo w tym programie dostrzec prawą stronę produkcji dla
symbolu ![]() , a także aksjomat.
, a także aksjomat.
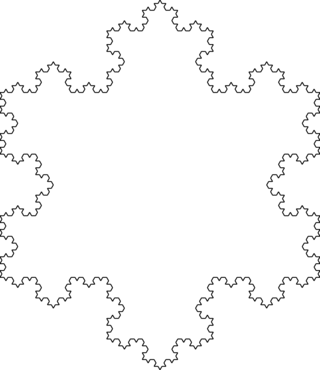
Otrzymany rysunek przedstawia przybliżenie znanej krzywej fraktalowej, który po raz pierwszy badał Helge von Koch w 1904r. Inny przykład zastosowania L-systemu do generacji figury fraktalowej mamy poniżej.
Pominięte są tu produkcje dla symboli ![]() ,
, ![]() ,
, ![]() , ponieważ powodują
one przepisanie tych symboli bez zmiany i szkoda miejsca. Zauważmy, że tu
symbol
, ponieważ powodują
one przepisanie tych symboli bez zmiany i szkoda miejsca. Zauważmy, że tu
symbol ![]() ,,zostaje” we wszystkich następnych napisach i nie powoduje
dokładania żadnych nowych symboli; tę rolę spełniają dwa symbole,
,,zostaje” we wszystkich następnych napisach i nie powoduje
dokładania żadnych nowych symboli; tę rolę spełniają dwa symbole, ![]() i
i ![]() , które nie oddziaływają na żółwia bezpośrednio.
, które nie oddziaływają na żółwia bezpośrednio.
%!
... % tu procedury TF, TPlus, TMinus
/L {
/iter iter 1 add def
iter itn ne {
Plus R F Minus L F L Minus F R Plus
} if
/iter iter 1 sub def
} def
/R {
/iter iter 1 add def
iter itn ne {
Minus L F Plus R F R Plus F L Minus
} if
/iter iter 1 sub def
} def
/F { TF } def
/Plus { TPlus } def
/Minus { TMinus } def
/dist 10 def
/dalpha 90 def
/iter 0 def
/itn 6 def
/x 140 def
/y 200 def
/alpha 90 def
R
showpage
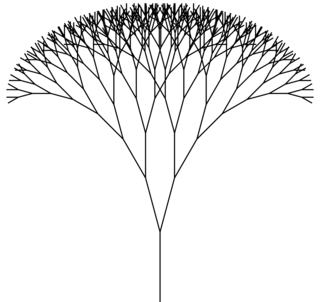
Aby narysować roślinkę, trzeba umieć wytwarzać rozgałęzienia krzywych.
Przydają się do tego symbole tradycyjnie oznaczane nawiasami kwadratowymi
(ponieważ symbole [ i ] są w PostScripcie zarezerwowane dla
innych celów, więc użyjemy nazw TLBrack i TRBrack),
pierwszy z nich powoduje
zapamiętanie bieżącego położenia i orientacji żółwia, a drugi —
przywrócenie ich. W PostScripcie moglibyśmy wykorzystać do tego stos
argumentów, ale to by utrudniło korzystanie z niego w innym celu; dlatego
lepiej zadeklarować odpowiednią tablicę i użyć jej w charakterze stosu.
/TInitStack {
/MaxTStack 120 def
/TStack MaxTStack array def
/TSP 0 def
} def
/TLBrack {
TSP 3 add MaxTStack le {
TStack TSP x put /TSP TSP 1 add def
TStack TSP y put /TSP TSP 1 add def
TStack TSP alpha put /TSP TSP 1 add def
} if
} def
/TRBrack {
TSP 3 ge {
/TSP TSP 1 sub def /alpha TStack TSP get def
/TSP TSP 1 sub def /y TStack TSP get def
/TSP TSP 1 sub def /x TStack TSP get def
} if
} def
Użyjemy tych procedur w programie (od razu ćwiczenie: proszę odtworzyć opis L-systemu, tj. alfabet, aksjomat i produkcje, realizowanego przez ten program):
%!
... % tu procedury obsługi żółwia
/F {
/iter iter 1 add def
iter itn eq { TF }
{
F LBrack Plus F RBrack F LBrack Minus F RBrack F
} ifelse
/iter iter 1 sub def
} def
/Plus { TPlus } def
/Minus { TMinus } def
/LBrack { TLBrack } def
/RBrack { TRBrack } def
/dist 20 def
/dalpha 30 def
/iter 0 def
/itn 4 def
/x 200 def
/y 100 def
/alpha 90 def
TInitStack
F
showpage
Symbol ![]() może być interpretowany jako polecenie wygenerowania krawędzi
wielokąta i wtedy można wprowadzić symbole
może być interpretowany jako polecenie wygenerowania krawędzi
wielokąta i wtedy można wprowadzić symbole ![]() i
i ![]() , czyli klamry,
które określają początek i koniec generowania wielokąta. Można też
generować wierzchołki wielokąta — niech to będzie skutkiem
interpretacji symbolu
, czyli klamry,
które określają początek i koniec generowania wielokąta. Można też
generować wierzchołki wielokąta — niech to będzie skutkiem
interpretacji symbolu ![]() ; wierzchołek pojawi się w bieżącym punkcie
położenia żółwia, który przemieszczany podczas przetwarzania symbolu
; wierzchołek pojawi się w bieżącym punkcie
położenia żółwia, który przemieszczany podczas przetwarzania symbolu
![]() nie rysuje kresek.
nie rysuje kresek.
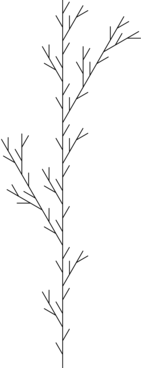
Zaprogramujemy L-system
ktory umożliwia wygenerowanie pokazanego na obrazku liścia.
%!
... % procedury TF, TPlus, TMinus, TRBrack, TLBrack
% jak poprzednio, a Tf proszę samemu napisać
/TLBrace { newpath /empty true def } def
/TRBrace { closepath stroke } def
/TDot {
empty { x y moveto } { x y lineto } ifelse
/empty false def
} def
/A {
/iter iter 1 add def
iter itn ne
{ LBrack Plus A LBrace Dot RBrack Dot C Dot
RBrace } if
/iter iter 1 sub def
} def
/B {
/iter iter 1 add def
iter itn ne
{ LBrack Minus B LBrace Dot RBrack Dot C Dot
RBrace } if
/iter iter 1 sub def
} def
/C {
/iter iter 1 add def
iter itn ne
{ f C } if
/iter iter 1 sub def
} def
/F { TF } def
/f { Tf } def
/Plus { TPlus } def
/Minus { TMinus } def
/LBrack { TLBrack } def
/RBrack { TRBrack } def
/LBrace { TLBrace } def
/RBrace { TRBrace } def
/Dot { TDot } def
/dist 20 def
/dalpha 10 def
/iter 0 def
/itn 20 def
/x 300 def
/y 200 def
/alpha 90 def
TInitStack
F F F F LBrack A RBrack LBrack B RBrack
showpage
13.12. PostScript obudowany
Zgodnie z podaną wcześniej informacją, aby system operacyjny uznał
plik tekstowy za program źródłowy w PostScripcie, pierwszymi dwoma znakami
w tym pliku powinny być Wysyłając taki plik na drukarkę,
otrzymamy odpowiedni obrazek, a~nie treść pliku. Taka minimalna informacja
często jednak nie wystarczy. Jeśli chcemy wygenerować obrazek, który
ma być ilustracją tekstu (złożonego np.\ za pomocą \TeX-a), to
trzeba dać dwie linie, o~postaci
\par\begin{ps}
\end{ps}
\parPierwsza z~tych linii musi być na początku pliku. Informuje ona program,
który ten plik przetwarza, że jest to tzw.\ PostScript obudowany,
czyli program opisujący obrazek przeznaczony do umieszczenia w~większej
całości. Druga linia (może być zaraz po pierwszej lub na końcu pliku)
zawiera informacje o~prostokącie, w~którym obrazek się mieści.
Program \TeX\ po przeczytaniu tej informacji zostawi na stronie
odpowiedni obszar na obrazek; cztery liczby całkowite są współrzędnymi
dolnego lewego i~górnego prawego narożnika, prostokąta.
Jednostka długości jest równa $1/72”$.
\parProgram w~PostScripcie obudowanym nie powinien zawierać instrukcji niszczących,
takich jak kasowanie strony lub zdejmowanie ze stosu obiektów, których
tam nie włożył. Nie należy też bezpośrednio przypisywać wartości~CTM;
to spowodowałoby umieszczenie obrazka w~ustalonym miejscu na stronie, a~nie
w~miejscu wyznaczonym przez program dokonujący składu, który ten obrazek
wciąga na ilus\-tra\-cję. Najlepiej, aby program utworzył własny słownik,
tylko z~niego korzystał, a~na końcu po sobie posprzątał.
\par\mode<all>
\par