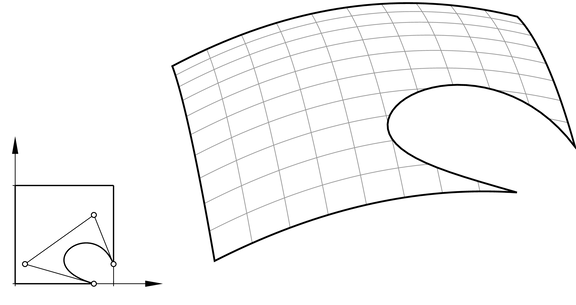Zagadnienia
6. Elementy modelowania geometrycznego
6.1. Krzywe Béziera
6.1.1. Określenie krzywych Béziera
Nazwa ,,krzywa Béziera” stopnia ![]() oznacza reprezentację krzywej
parametrycznej w postaci ciągu punktów
oznacza reprezentację krzywej
parametrycznej w postaci ciągu punktów ![]() ,
tzw. punktów kontrolnych, które należy podstawić do wzoru
,
tzw. punktów kontrolnych, które należy podstawić do wzoru
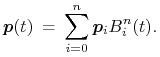 |
Występujące w nim funkcje ![]() to wielomiany Bernsteina
stopnia
to wielomiany Bernsteina
stopnia ![]() , określone wzorem
, określone wzorem
Powyższą reprezentację krzywych i stanowiąca jej rozwinięcie reprezentację płatów powierzchni we wczesnych latach tysiąc dziewięćset sześćdziesiątych opracowali niezależnie Pierre Bézier i Paul de Faget de Casteljau, na potrzeby firm Renault i Citroën. Dzięki swoim zaletom, takim jak łatwość interakcyjnego kształtowania i istnienie sprawnych algorytmów przetwarzania, reprezentacje te obecnie używane powszechnie nie tylko w inżynierskich systemach projektowania wspomaganego komputerem, ale także w wielu innych zastosowaniach graficznych (np. w projektowaniu czcionek).
6.1.2. Algorytm de Casteljau
Dla dowolnego ![]() punkt
punkt ![]() można obliczyć za pomocą
algorytmu de Casteljau, realizowanego przez
następujący podprogram:
można obliczyć za pomocą
algorytmu de Casteljau, realizowanego przez
następujący podprogram:
| { |
| for |
| for |
| |
| { |
Udowodnimy, że punkt ![]() jest punktem
jest punktem ![]() obliczonym
przez powyższą procedurę.
Jeśli
obliczonym
przez powyższą procedurę.
Jeśli ![]() , to krzywa jest zdegenerowana do jednego punktu, czyli
, to krzywa jest zdegenerowana do jednego punktu, czyli
![]() ,
ponieważ
,
ponieważ ![]() dla
każdego
dla
każdego ![]() . Załóżmy, że
. Załóżmy, że ![]() . Najpierw obliczymy
. Najpierw obliczymy
oraz dla ![]()
Następnie przyjmiemy założenie indukcyjne, że punkty
![]() i
i ![]() są odpowiadającymi danej
wartości parametru
są odpowiadającymi danej
wartości parametru ![]() punktami krzywych Béziera stopnia
punktami krzywych Béziera stopnia ![]() ,
reprezentowanych przez punkty kontrolne odpowiednio
,
reprezentowanych przez punkty kontrolne odpowiednio
![]() i
i ![]() . Na
podstawie pokazanego wyżej rekurencyjnego związku między wielomianami
Bernsteina stopni
. Na
podstawie pokazanego wyżej rekurencyjnego związku między wielomianami
Bernsteina stopni ![]() i
i ![]() , mamy
, mamy
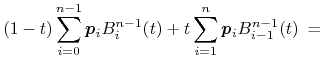 |
|||
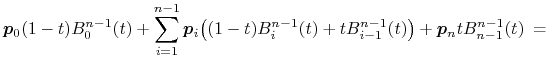 |
|||
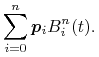 |
Wielu podanych dalej własności krzywych Béziera i B-sklejanych dowodzi się w podobny sposób.
Algorytm de Casteljau ma oprócz obliczania punktów krzywej wiele innych zastosowań, o których będzie dalej.
6.1.3. Własności krzywych Béziera
Krzywe Béziera mają następujące własności:
-
Niezmienniczość afiniczna reprezentacji. Suma wielomianów Bernsteina stopnia
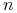 jest równa
jest równa 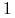 , a zatem dla dowolnego
, a zatem dla dowolnego 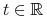 punkt
punkt 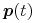 jest kombinacją afiniczną punktów kontrolnych.
Ponieważ przekształcenia afiniczna zachowują kombinacje afiniczne,
więc dla ustalonego przekształcenia afinicznego
jest kombinacją afiniczną punktów kontrolnych.
Ponieważ przekształcenia afiniczna zachowują kombinacje afiniczne,
więc dla ustalonego przekształcenia afinicznego 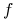 i dla
każdego
i dla
każdego 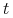 odpowiedni punkt krzywej Béziera reprezentowanej
przez punkty kontrolne
odpowiedni punkt krzywej Béziera reprezentowanej
przez punkty kontrolne  jest równy
jest równy
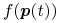 . Innymi słowy, aby otrzymać obraz krzywej Béziera
w dowolnym przekształceniu afinicznym, wystarczy
poddać temu przekształceniu jej punkty kontrolne.
. Innymi słowy, aby otrzymać obraz krzywej Béziera
w dowolnym przekształceniu afinicznym, wystarczy
poddać temu przekształceniu jej punkty kontrolne. -
Własność otoczki wypukłej. Dla
![t\in[0,1]](wyklady/gk1/mi/mi155.png) punkt
punkt
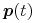 jest kombinacją wypukłą punktów kontrolnych
(wielomiany Bernsteina są w przedziale
jest kombinacją wypukłą punktów kontrolnych
(wielomiany Bernsteina są w przedziale ![[0,1]](wyklady/gk1/mi/mi180.png) nieujemne), a więc
należy do otoczki wypukłej ich zbioru.
nieujemne), a więc
należy do otoczki wypukłej ich zbioru. -
Zachodzi interpolacja skrajnych punktów kontrolnych:

-
Dla
![t\in[0,1]](wyklady/gk1/mi/mi155.png) krzywa Béziera nie ma z żadną prostą (na
płaszczyźnie) albo płaszczyzną (w przestrzeni) większej liczby
punktów przecięcia niż jej łamana kontrolna (to się nazywa
własnością zmniejszania wariacji).
krzywa Béziera nie ma z żadną prostą (na
płaszczyźnie) albo płaszczyzną (w przestrzeni) większej liczby
punktów przecięcia niż jej łamana kontrolna (to się nazywa
własnością zmniejszania wariacji). -
Istnieje możliwość podwyższenia stopnia, czyli znalezienia reprezentacji stopnia
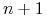 . Związek obu reprezentacji
wyraża się wzorami
. Związek obu reprezentacji
wyraża się wzorami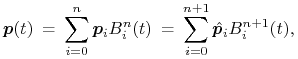
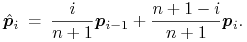
Podwyższanie stopnia możemy iterować, dostając reprezentacje coraz wyższych stopni. Ciąg łamanych kontrolnych otrzymanych w ten sposób zbiega jednostajnie do krzywej dla
![t\in[0,1]](wyklady/gk1/mi/mi155.png) .
Zbieżność tego ciągu jest jednak zbyt wolna, aby miała praktyczne znaczenie.
.
Zbieżność tego ciągu jest jednak zbyt wolna, aby miała praktyczne znaczenie. -
Jeśli kolejne punkty kontrolne leżą na prostej, w kolejności indeksów i w równych odstępach, to krzywa Béziera jest odcinkiem sparametryzowanym ze stałą prędkością. Najłatwiej jest udowodnić to rozpatrując reprezentację odcinka w postaci krzywej Béziera stopnia
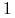 i jego reprezentacje otrzymane przez podwyższanie stopnia.
i jego reprezentacje otrzymane przez podwyższanie stopnia. -
Pochodna krzywej Béziera o punktach kontrolnych
 wyraża się wzorem
wyraża się wzorem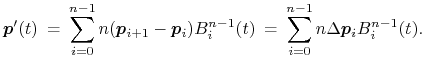
Na podstawie własności otoczki wypukłej mamy więc własność hodografu, według której kierunek wektora
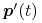 dla
dla
![t\in[0,1]](wyklady/gk1/mi/mi155.png) jest zawarty w stożku rozpiętym przez wektory
jest zawarty w stożku rozpiętym przez wektory
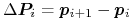 dla
dla  .
Ponadto zachodzą równości
.
Ponadto zachodzą równości
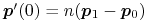 oraz
oraz 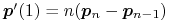 .
. -
Podział krzywej. Punkty
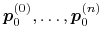 oraz
oraz
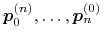 , otrzymane w trakcie wykonywania
algorytmu de Casteljau, są punktami kontrolnymi tej samej krzywej,
w innych parametryzacjach. Dokładniej, dla dowolnego
, otrzymane w trakcie wykonywania
algorytmu de Casteljau, są punktami kontrolnymi tej samej krzywej,
w innych parametryzacjach. Dokładniej, dla dowolnego 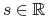 zachodzą równości
zachodzą równości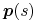
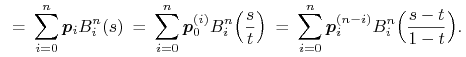
Aby narysować krzywą, możemy dzielić ją na ,,dostatecznie krótkie” łuki i rysować zamiast nich odcinki. Możemy użyć w tym celu procedury rekurencyjnej (porównaj ją z przedstawioną wcześniej procedurą rysowania elipsy):
procedure r_Krzywa ( 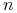 ,
, 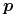 );
);begin if dostatecznie blisko ( ![\bm{p}[0]](wyklady/gk1/mi/mi1371.png) ,
, ![\bm{p}[n]](wyklady/gk1/mi/mi1383.png) )
)then rysuj odcinek ( ![\bm{p}[0]](wyklady/gk1/mi/mi1371.png) ,
, ![\bm{p}[n]](wyklady/gk1/mi/mi1383.png) );
);else begin ![\bm{q}[0]](wyklady/gk1/mi/mi1355.png) :=
:= ![\bm{p}[0]](wyklady/gk1/mi/mi1371.png) ;
;for 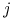 :=
:= 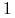 to
to 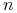 do begin
do beginfor 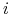 :=
:= 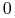 to
to 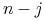 do
do![\bm{p}[i]](wyklady/gk1/mi/mi1386.png) :=
:= ![\frac{1}{2}(\bm{p}[i]+\bm{p}[i+1])](wyklady/gk1/mi/mi1391.png) ;
;![\bm{q}[j]](wyklady/gk1/mi/mi1387.png) :=
:= ![\bm{p}[0]](wyklady/gk1/mi/mi1371.png)
end; r_Krzywa ( 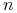 ,
, 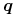 );
);r_Krzywa ( 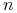 ,
, 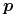 )
)end end {r_Krzywa}; Otoczka wypukła łamanej kontrolnej ,,całej” krzywej jest z reguły znacznie większa niż suma otoczek łamanych kontrolnych kilku jej fragmentów, a zatem przez podział możemy uzyskiwać znacznie dokładniejsze oszacowania położenia krzywej.
-
Algorytm szybkiego obliczania punktu
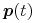 (o koszcie
(o koszcie 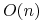 zamiast
zamiast
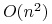 , jak w przypadku algorytmu de Casteljau) możemy uzyskać,
adaptując schemat Hornera. Podstawiając
, jak w przypadku algorytmu de Casteljau) możemy uzyskać,
adaptując schemat Hornera. Podstawiając 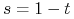 , otrzymujemy
, otrzymujemy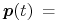
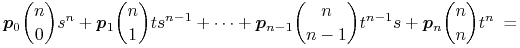
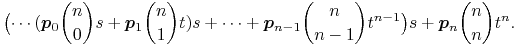
Schemat Hornera ze względu na
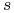 trzeba tylko uzupełnić o obliczanie
wektorów
trzeba tylko uzupełnić o obliczanie
wektorów
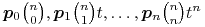 .
Ponieważ
.
Ponieważ 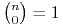 i
i 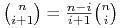 ,
więc mamy stąd algorytm
,
więc mamy stąd algorytm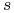 :=
:= 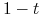 ;
;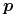 :=
:= 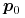 ;
;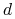 :=
:= 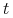 ;
;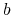 :=
:= 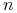 ;
;for 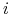 :=
:= 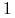 to
to 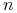 do begin
do begin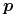 :=
:= 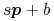 *
*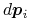 ;
;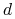 :=
:= 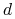 *
*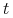 ;
;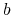 :=
:= 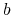 *
*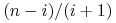
end; { 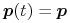 }
}
6.2. Krzywe B-sklejane
6.2.1. Określenie krzywych B-sklejanych
Modelowanie figur o skomplikowanym kształcie wymagałoby użycia krzywych Béziera wysokiego stopnia, co oprócz niewygody (z punktu widzenia użytkownika programu interakcyjnego) sprawiałoby różne kłopoty implementacyjne (bardzo duże wartości współczynników dwumianowych, wysoki koszt algorytmów obliczania punktu). Dlatego często stosuje się krzywe kawałkami wielomianowe w reprezentacji B-sklejanej; jest ona uogólnieniem reprezentacji Béziera krzywych wielomianowych.
Krzywa B-sklejana jest określona przez podanie: stopnia ![]() , ciągu
, ciągu
![]() węzłów
węzłów ![]() (ciąg ten powinien być niemalejący, a
ponadto
(ciąg ten powinien być niemalejący, a
ponadto ![]() powinno być większe od
powinno być większe od ![]() ), oraz
), oraz ![]() punktów
kontrolnych
punktów
kontrolnych ![]() . Wzór, który jest definicją
krzywej B-sklejanej ma postać
. Wzór, który jest definicją
krzywej B-sklejanej ma postać
![\displaystyle\bm{s}(t)=\sum _{{i=0}}^{{N-n-1}}\bm{d}_{i}N^{n}_{i}(t),\quad t\in[u_{n},u_{{N-n}}].](wyklady/gk1/mi/mi647.png) |
We wzorze tym występują funkcje B-sklejane ![]() stopnia
stopnia ![]() ,
które są określone przez ustalony ciąg węzłów.
,
które są określone przez ustalony ciąg węzłów.
Istnieje kilka definicji funkcji B-sklejanych, które różnią się stopniem skomplikowania, a także trudnością dowodzenia na podstawie takiej definicji różnych własności tych funkcji (w zasadzie więc wychodzi na jedno, której definicji użyjemy, jeśli chcemy dowodzić twierdzenia, to trudności nie da się uniknąć). Ponieważ w tym wykładzie ograniczamy się do praktycznych aspektów zagadnienia, więc przytoczę rekurencyjny wzór Mansfielda-de Boora-Coxa, który w książkach o grafice chyba najczęściej pełni rolę definicji:
| (6.1) | ||||
| (6.2) |
Wzór ten jest uogólnieniem rozważanego wcześniej wzoru wiążącego
wielomiany Bernsteina stopni ![]() i
i ![]() .
.
6.2.2. Algorytm de Boora
Na podstawie wzoru Mansfielda-de Boora-Coxa łatwo jest otrzymać
algorytm de Boora obliczania punktu ![]() na podstawie
danych opisujących krzywą
na podstawie
danych opisujących krzywą ![]() i parametru
i parametru ![]() . Algorytm ten jest
uogólnieniem algorytmu de Casteljau i jest realizowany przez
następujące instrukcje:
. Algorytm ten jest
uogólnieniem algorytmu de Casteljau i jest realizowany przez
następujące instrukcje:
| { |
| while |
| while ( |
| for |
| for |
| |
| |
| end; |
| { |
6.2.3. Podstawowe własności krzywych B-sklejanych
Własności krzywych B-sklejanych najbardziej istotne w zastosowaniach związanych z grafiką komputerową, są takie:
-
Jeśli wszystkie węzły od
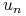 do
do 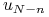 są różne (tworzą
ciąg rosnący), to krzywa składa się z
są różne (tworzą
ciąg rosnący), to krzywa składa się z 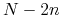 łuków
wielomianowych. W przeciwnym razie (jeśli występują tzw. węzły
krotne), to liczba łuków jest mniejsza.
łuków
wielomianowych. W przeciwnym razie (jeśli występują tzw. węzły
krotne), to liczba łuków jest mniejsza. -
Algorytm de Boora dokonuje liniowej interpolacji kolejno otrzymywanych punktów (liczby
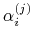 należą do przedziału
należą do przedziału
![[0,1]](wyklady/gk1/mi/mi180.png) ); stąd wynika silna własność otoczki wypukłej:
wszystkie punkty łuku dla
); stąd wynika silna własność otoczki wypukłej:
wszystkie punkty łuku dla ![t\in[u_{k},u_{{k+1}}]](wyklady/gk1/mi/mi618.png) leżą w otoczce
wypukłej punktów
leżą w otoczce
wypukłej punktów 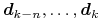 .
Mamy też afiniczną niezmienniczość tej reprezentacji
krzywej; aby otrzymać jej obraz w dowolnym przekształceniu afinicznym,
wystarczy zastosować to przekształcenie do punktów kontrolnych
.
Mamy też afiniczną niezmienniczość tej reprezentacji
krzywej; aby otrzymać jej obraz w dowolnym przekształceniu afinicznym,
wystarczy zastosować to przekształcenie do punktów kontrolnych
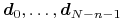 .
. -
Lokalna kontrola kształtu. Ponieważ punkt
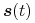 dla
dla
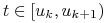 zależy tylko od punktów
zależy tylko od punktów
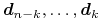 , więc zmiana punktu
, więc zmiana punktu 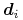 powoduje
zmianę fragmentu krzywej dla
powoduje
zmianę fragmentu krzywej dla ![t\in[u_{i},u_{{i+n+1}}]](wyklady/gk1/mi/mi761.png) .
. -
Pochodna krzywej B-sklejanej stopnia
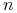 jest krzywą stopnia
jest krzywą stopnia 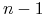 :
: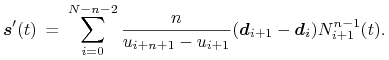
Funkcje B-sklejane
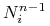 występujące w powyższym wzorze
są określone dla tego samego ciągu węzłów, co funkcje
występujące w powyższym wzorze
są określone dla tego samego ciągu węzłów, co funkcje 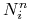 w określeniu krzywej
w określeniu krzywej 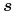 . Zastosowanie
(silnej) własności otoczki wypukłej do pochodnej daje (silną)
własność hodografu krzywych B-sklejanych.
. Zastosowanie
(silnej) własności otoczki wypukłej do pochodnej daje (silną)
własność hodografu krzywych B-sklejanych.
-
W otoczeniu węzła o krotności
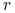 krzywa jest klasy
krzywa jest klasy 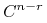 (dowód na podstawie wzoru Mansfielda-de Boora-Coxa, który
przyjęliśmy tu za definicję, jest pracochłonny, ale reguła
jest prosta, więc warto ją zapamiętać).
(dowód na podstawie wzoru Mansfielda-de Boora-Coxa, który
przyjęliśmy tu za definicję, jest pracochłonny, ale reguła
jest prosta, więc warto ją zapamiętać). -
Jeśli dwa sąsiednie węzły są
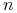 -krotne, to łuk krzywej
między nimi jest krzywą Béziera; dokładniej, jeśli
-krotne, to łuk krzywej
między nimi jest krzywą Béziera; dokładniej, jeśli
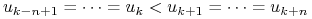 ,
to dla
,
to dla ![t\in[u_{k},u_{{k+1}}]](wyklady/gk1/mi/mi618.png) mamy
mamy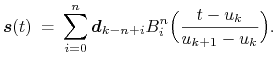
6.2.4. Wstawianie węzła
Wstawianie węzła jest procedurą, która zmienia reprezentację krzywej, nie zmieniając samej krzywej. W wyniku zastosowania tej procedury otrzymujemy reprezentację o większej liczbie węzłów i punktów kontrolnych. Idea postępowania, które prowadzi do otrzymania tej reprezentacji może być przedstawiona w następujących krokach
-
Określamy tak zwane współrzędne Greville'a:
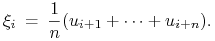
Będziemy (w myśli) przekształcać łamaną o wierzchołkach
![\bm{f}_{i}=[\xi _{i},\bm{d}_{i}]](wyklady/gk1/mi/mi669.png) .
. -
Dołączamy liczbę
![t\in[u_{n},u_{{N-n}}]](wyklady/gk1/mi/mi749.png) (wstawiany węzeł) do
wyjściowego ciągu węzłów, z zachowaniem uporządkowania.
(wstawiany węzeł) do
wyjściowego ciągu węzłów, z zachowaniem uporządkowania. -
Obliczamy nowe współrzędne Greville'a
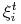 , odpowiadające
ciągowi węzłów z dołączoną liczbą
, odpowiadające
ciągowi węzłów z dołączoną liczbą 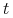 .
. -
Znajdujemy punkty
![\bm{f}_{i}^{t}=[\xi _{i}^{t},\bm{d}_{i}^{t}]](wyklady/gk1/mi/mi810.png) na łamanej. Punkty
na łamanej. Punkty
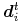 są punktami kontrolnymi nowej reprezentacji krzywej.
są punktami kontrolnymi nowej reprezentacji krzywej.
Praktyczna implementacja procedury wstawiania węzła nie musi obliczać współrzędnych Greville'a, które pełnią tu rolę pomocniczą. Równoważny skutek daje następujący podprogram:
| { |
| { |
| while |
| |
| while ( |
| begin |
| for |
| |
| for |
| |
| for |
| |
| { zmienna |
Własności tego przekształcenia reprezentacji krzywej są następujące:
-
Po wstawieniu węzła liczba punktów kontrolnych jest większa o
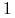 .
. -
Wynik wstawienia kilku węzłów nie zależy od kolejności ich wstawiania.
-
Krzywa reprezentowana przez nowy ciąg węzłów i nowy ciąg punktów kontrolnych jest identyczna z krzywą wyjściową.
-
Algorytm de Boora jest procedurą wstawiania węzła, powtórzoną tyle razy, aby ostatecznie otrzymać
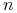 -krotny węzeł
-krotny węzeł
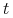 .
. -
Po wstawieniu dostatecznie wielu węzłów (tak, aby ich odległości stały się dostatecznie małe), otrzymujemy łamaną kontrolną, która jest dowolnie bliska krzywej. Odległość odpowiednio sparametryzowanej łamanej kontrolnej od reprezentowanej przez nią krzywej B-sklejanej jest proporcjonalna do
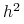 , gdzie
, gdzie
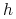 oznacza maksymalną odległość sąsiednich węzłów. Datego
po wstawieniu nawet niezbyt dużej liczby węzłów możemy otrzymać
łamaną, którą można narysować w celu uzyskania dość
dokładnego obrazu krzywej.
oznacza maksymalną odległość sąsiednich węzłów. Datego
po wstawieniu nawet niezbyt dużej liczby węzłów możemy otrzymać
łamaną, którą można narysować w celu uzyskania dość
dokładnego obrazu krzywej.
Procedurę wstawiania węzła możemy wykorzystać tak:
-
wybieramy początkowo małą liczbę węzłów i punktów kontrolnych w celu zgrubnego ukształtowania krzywej,
-
wstawiamy pewną liczbę dodatkowych węzłów,
-
poprawiamy krzywą w celu wymodelowania szczegółów.
Inne zastosowanie to wstawienie węzłów tak, aby krotność
wszystkich węzłów była równa ![]() ; łamana kontrolna składa się
wtedy z łamanych kontrolnych Béziera poszczególnych łuków
wielomianowych, które można narysować za pomocą jakiejś szybkiej
procedury, np. opartej na schemacie Hornera. Procedury rysowania krzywych
Béziera mogą być zaimplementowane w sprzęcie. Mając procedurę
wstawiania węzłów, możemy użyć takiego sprzętu do rysowania krzywych
B-sklejanych.
; łamana kontrolna składa się
wtedy z łamanych kontrolnych Béziera poszczególnych łuków
wielomianowych, które można narysować za pomocą jakiejś szybkiej
procedury, np. opartej na schemacie Hornera. Procedury rysowania krzywych
Béziera mogą być zaimplementowane w sprzęcie. Mając procedurę
wstawiania węzłów, możemy użyć takiego sprzętu do rysowania krzywych
B-sklejanych.
6.2.5. Krzywe B-sklejane z węzłami równoodległymi
Narzucenie węzłów równoodległych ogranicza klasę krzywych B-sklejanych, ale jednocześnie upraszcza wzory i umożliwia stosowanie specjalnych algorytmów.
Przypuśćmy (bez straty ogólności), że dana krzywa jest reprezentowana
przez nieskończony ciąg węzłów, składający się z wszystkich liczb
całkowitych, i nieskończony ciąg punktów kontrolnych ![]() ;
mamy zatem
;
mamy zatem
gdzie każda funkcja B-sklejana ![]() stopnia
stopnia ![]() przyjmuje wartości
różne od zera tylko w przedziale
przyjmuje wartości
różne od zera tylko w przedziale ![]() . Ponadto dla
każdego
. Ponadto dla
każdego ![]() oraz
oraz ![]() mamy
mamy ![]() .
.
Rozważmy teraz nieskończony ciąg węzłów, składający się z wszystkich
całkowitych wielokrotności liczby ![]() .
Niech
.
Niech ![]() oznacza funkcję B-sklejaną opartą na tym ciągu węzłów
i przyjmującą niezerowe wartości w przedziale
oznacza funkcję B-sklejaną opartą na tym ciągu węzłów
i przyjmującą niezerowe wartości w przedziale
![]() . Krzywą
. Krzywą ![]() możemy
przedstawić w postaci
możemy
przedstawić w postaci
Na podstawie danych punktów ![]() należy znaleźć punkty
należy znaleźć punkty ![]() .
.
Algorytm Lane'a-Riesenfelda, który rozwiązuje to zadanie, podaję
bez dowodu. Algorytm ten składa się z dwóch etapów. Pierwszy z nich to
podwajanie: konstruujemy punkty
![]() . W drugim etapie wykonujemy
. W drugim etapie wykonujemy
![]() -krotnie operację uśredniania: obliczamy punkty
-krotnie operację uśredniania: obliczamy punkty
![]() .
Mając daną początkową reprezentację krzywej
.
Mając daną początkową reprezentację krzywej ![]() w postaci łamanej o wierzchołkach
w postaci łamanej o wierzchołkach ![]() ,
w kolejnych krokach uśredniania otrzymamy łamane o wierzchołkach
,
w kolejnych krokach uśredniania otrzymamy łamane o wierzchołkach
![]() .
Wynikiem obliczenia są punkty
.
Wynikiem obliczenia są punkty ![]() dla
każdego
dla
każdego ![]() .
.
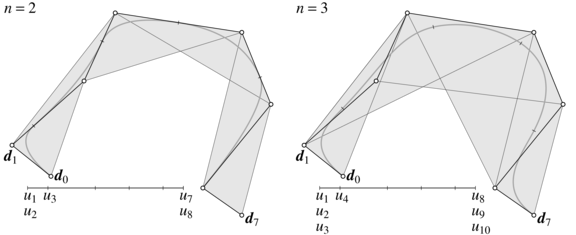
Wyniki działania algorytmu dla krzywych stopnia ![]() ,
, ![]() i
i ![]() są pokazane na
rysunku 6.11. Otrzymaną łamaną można następnie użyć jako dane
dla algorytmu Lane'a-Riesenfelda i otrzymać łamaną reprezentującą
krzywą
są pokazane na
rysunku 6.11. Otrzymaną łamaną można następnie użyć jako dane
dla algorytmu Lane'a-Riesenfelda i otrzymać łamaną reprezentującą
krzywą ![]() przy użyciu ciągu węzłów
przy użyciu ciągu węzłów ![]() itd.
Określony w ten sposób nieskończony ciąg łamanych, z których każda
jest reprezentacją krzywej związaną z odpowiednim ciągiem węzłów
równoodległych, jest szybko zbieżny do krzywej, można zatem narysować
jedną z tych łamanych zamiast krzywej.
itd.
Określony w ten sposób nieskończony ciąg łamanych, z których każda
jest reprezentacją krzywej związaną z odpowiednim ciągiem węzłów
równoodległych, jest szybko zbieżny do krzywej, można zatem narysować
jedną z tych łamanych zamiast krzywej.
6.3. Powierzchnie Béziera i B-sklejane
6.3.1. Płaty tensorowe
Do określenia powierzchni potrzebne są funkcje dwóch zmiennych. Najczęściej wykorzystuje się iloczyn tensorowy przestrzeni funkcji jednej zmiennej. Użycie go prowadzi do wzorów
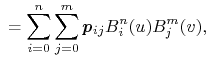 |
|||
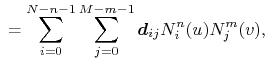 |
które opisują odpowiednio płat powierzchni Béziera i płat
powierzchni B-sklejanej stopnia ![]() . W przypadku płata B-sklejanego,
nawet jeśli stopień ze względu na każdy parametr jest taki sam, można
podać inny ciąg węzłów określających funkcje bazowe.
. W przypadku płata B-sklejanego,
nawet jeśli stopień ze względu na każdy parametr jest taki sam, można
podać inny ciąg węzłów określających funkcje bazowe.
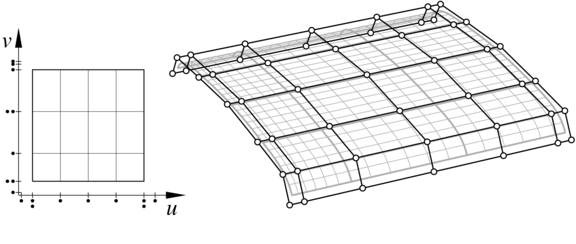
Dziedziną płata Béziera jest zwykle kwadrat jednostkowy. Dziedziną
płata B-sklejanego jest prostokąt ![]() .
Często dziedzinę otrzymuje się przez odrzucenie fragmentów takiego
prostokąta; mamy wtedy płat obcięty (rys. 6.13).
.
Często dziedzinę otrzymuje się przez odrzucenie fragmentów takiego
prostokąta; mamy wtedy płat obcięty (rys. 6.13).
Punkty kontrolne płata każdego z tych rodzajów dla wygody kształtowania
przedstawia się w postaci siatki. Wyróżniamy w niej
wiersze i kolumny. Wyznaczenie punktu na powierzchni, dla
ustalonych parametrów ![]() ,
, ![]() , można sprowadzić do wyznaczania punktów
na krzywych (Béziera albo B-sklejanych), np.
, można sprowadzić do wyznaczania punktów
na krzywych (Béziera albo B-sklejanych), np.
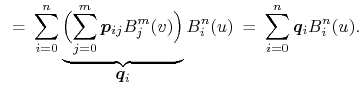 |
Wszystkie działania wykonujemy na kolumnach siatki, traktując je tak,
jakby to były łamane kontrolne krzywych. Punkty tych krzywych,
odpowiadające ustalonemu ![]() , są punktami kontrolnymi krzywej stałego
parametru
, są punktami kontrolnymi krzywej stałego
parametru ![]() leżącymi na płacie. Można też postąpić w odwrotnej
kolejności i najpierw przetwarzać wiersze, a potem kolumnę otrzymanych
punktów.
leżącymi na płacie. Można też postąpić w odwrotnej
kolejności i najpierw przetwarzać wiersze, a potem kolumnę otrzymanych
punktów.
Zasada przetwarzania reprezentacji płata w celu podwyższenia stopnia, podziału na kawałki, wstawienia węzła i obliczenia pochodnych cząstkowych jest identyczna.
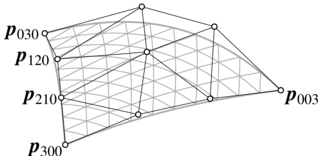
6.3.2. Płaty trójkątne
Dziedziną trójkątnego płata Béziera jest zwykle trójkąt,
którego wierzchołki stanowią układ odniesienia układu współrzędnych
barycentrycznych ![]() ,
, ![]() ,
, ![]() . Suma tych współrzędnych jest równa
. Suma tych współrzędnych jest równa ![]() ,
wewnątrz trójkąta mają one wartości dodatnie.
,
wewnątrz trójkąta mają one wartości dodatnie.
Płat jest określony wzorem
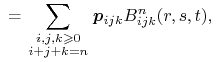 |
w którym występują wielomiany Bernsteina trzech zmiennych
stopnia ![]() i punkty kontrolne
i punkty kontrolne ![]() , będące
wierzchołkami siatki kontrolnej płata trójkątnego.
, będące
wierzchołkami siatki kontrolnej płata trójkątnego.
Algorytm wyznaczania punktu (algorytm de Casteljau) jest następujący:
| { |
| for |
| for |
| |
| { |
Podobnie jak w przypadku krzywych Béziera, algorytm de Casteljau pozwala
dokonać podziału płata. Punkty kontrolne jego fragmentów to odpowiednio
![]() ,
, ![]() ,
, ![]() . Jeśli
współrzędna
. Jeśli
współrzędna ![]() ,
, ![]() lub
lub ![]() jest równa
jest równa ![]() (punkt, któremu odpowiada
obliczony punkt na płacie, leży na boku trójkąta, który jest
dziedziną), to mamy możliwość podziału płata na dwa fragmenty.
Algorytm de Casteljau działa wtedy w taki sposób, jakby poszczególne
wiersze siatki kontrolnej były łamanymi kontrolnymi krzywych Béziera
stopni
(punkt, któremu odpowiada
obliczony punkt na płacie, leży na boku trójkąta, który jest
dziedziną), to mamy możliwość podziału płata na dwa fragmenty.
Algorytm de Casteljau działa wtedy w taki sposób, jakby poszczególne
wiersze siatki kontrolnej były łamanymi kontrolnymi krzywych Béziera
stopni ![]() .
.
6.3.3. Metody siatek
Algorytm Lane'a-Riesenfelda dla powierzchni B-sklejanych stopnia ![]() jest dwuwymiarową wersją algorytmu przedstawionego wcześniej dla krzywej.
Punkty
jest dwuwymiarową wersją algorytmu przedstawionego wcześniej dla krzywej.
Punkty ![]() , przy użyciu których powierzchnia sklejana
jest określona wzorem
, przy użyciu których powierzchnia sklejana
jest określona wzorem
z funkcjami B-sklejanymi stopnia ![]() opartymi na (tym samym) ciągu węzłów
całkowitych, posłużą do obliczenia punktów
opartymi na (tym samym) ciągu węzłów
całkowitych, posłużą do obliczenia punktów ![]() ,
takich że
,
takich że
gdzie funkcje ![]() są określone przy użyciu ciągu węzłów
są określone przy użyciu ciągu węzłów
![]() . Algorytm składa się z kroku podwajania
i
. Algorytm składa się z kroku podwajania
i ![]() kroków uśredniania, przy czym
kroków uśredniania, przy czym
-
W kroku podwajania przyjmujemy
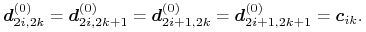
-
W kroku uśredniania dla
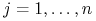 przyjmujemy
przyjmujemy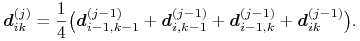
W ten sposób otrzymujemy nową siatkę kontrolną; powtarzając ten algorytm,
otrzymamy ciąg siatek szybko zbieżny do powierzchni ![]() .
Dowolną z tych siatek (otrzymaną np. po kilku, najwyżej kilkunastu
iteracjach) możemy uznać za dostatecznie dokładne przybliżenie
powierzchni i narysować zamiast niej.
.
Dowolną z tych siatek (otrzymaną np. po kilku, najwyżej kilkunastu
iteracjach) możemy uznać za dostatecznie dokładne przybliżenie
powierzchni i narysować zamiast niej.
Okazuje się, że opisane wyżej postępowanie daje się uogólnić na siatki nieregularne, tj. takie, których wierzchołków nie można ustawić w prostokątną tablicę. Rozważmy siatkę jako graf; wierzchołki siatki są wierzchołkami grafu, odcinki siatki są krawędziami grafu, możemy też określić ściany grafu, jako łamane zamknięte złożone z krawędzi, takie że odrzucenie wierzchołków i krawędzi łamanej nie likwiduje spójności grafu. Zakładamy, że każda krawędź należy do jednej lub do dwóch ścian.
Siatka jest regularna, jeśli wszystkie ściany
mają ![]() krawędzie i każdy wierzchołek nie leżący na brzegu siatki,
tzw. wewnetrzny, jest stopnia
krawędzie i każdy wierzchołek nie leżący na brzegu siatki,
tzw. wewnetrzny, jest stopnia ![]() (tj. jest incydentny z czterema
krawędziami). Każda ściana nie-czworokątna i każdy wierzchołek
wewnętrzny stopnia różnego od
(tj. jest incydentny z czterema
krawędziami). Każda ściana nie-czworokątna i każdy wierzchołek
wewnętrzny stopnia różnego od ![]() jest tzw. elementem specjalnym
siatki.
jest tzw. elementem specjalnym
siatki.
Dla siatki, która zawiera elementy specjalne, możemy określić operację
podwajania w ten sposób: każdy wierzchołek stopnia ![]() zastępujemy
przez ścianę (zdegenerowaną do punktu), która ma
zastępujemy
przez ścianę (zdegenerowaną do punktu), która ma ![]() wierzchołków
i krawędzi. Każdą krawędź zastępujemy przez ścianę czworokątną,
zdegenerowaną do odcinka; ściany dotychczasowe pozostawiamy (oczywiście,
w nowej siatce zmieni się numeracja wierzchołków każdej ściany).
Jeśli siatka jest regularna, to wynik jest taki sam jak wynik kroku
podwajania w algorytmie Lane'a-Riesenfelda dla powierzchni.
wierzchołków
i krawędzi. Każdą krawędź zastępujemy przez ścianę czworokątną,
zdegenerowaną do odcinka; ściany dotychczasowe pozostawiamy (oczywiście,
w nowej siatce zmieni się numeracja wierzchołków każdej ściany).
Jeśli siatka jest regularna, to wynik jest taki sam jak wynik kroku
podwajania w algorytmie Lane'a-Riesenfelda dla powierzchni.
Operację uśredniania określamy tak: konstruujemy graf dualny do siatki danej. Dla każdej ściany określamy wierzchołek, jako środek ciężkości wierzchołków tej ściany. Dla każdej krawędzi wspólnej dla dwóch ścian wprowadzamy krawędź łączącą wierzchołki skonstruowane dla tych ścian. Ściany nowej siatki odpowiadają wierzchołkom wewnętrznym siatki danej. Również taka operacja uśredniania jest dla siatki regularnej identyczna z uśrednianiem wykonywanym w algorytmie Lane'a-Riesenfelda. Zauważmy, że choć liczba wierzchołków, krawędzi i ścian rośnie podczas podwajania, ale żadna z opisanych operacji nie może powiększyć liczby elementów specjalnych w siatce.
Możemy teraz wykonać podwajanie, a następnie ![]() kroków uśredniania.
Dwa najczęściej stosowane przypadki, dla
kroków uśredniania.
Dwa najczęściej stosowane przypadki, dla ![]() oraz
oraz ![]() , są znane
odpowiednio jako algorytmy Doo-Sabina i Catmulla-Clarka. Iterując dowolny
z tych algorytmów, otrzymamy ciąg siatek zbieżny do powierzchni
granicznej. Powierzchnia ta prawie w całości składa się z kawałków
wielomianowych stopnia
, są znane
odpowiednio jako algorytmy Doo-Sabina i Catmulla-Clarka. Iterując dowolny
z tych algorytmów, otrzymamy ciąg siatek zbieżny do powierzchni
granicznej. Powierzchnia ta prawie w całości składa się z kawałków
wielomianowych stopnia ![]() ; wyjątkiem jest otoczenie punktów, do
których zbiegają elementy specjalne siatki.
; wyjątkiem jest otoczenie punktów, do
których zbiegają elementy specjalne siatki.
6.4. Krzywe i powierzchnie wymierne
Krzywe i powierzchnie Béziera i B-sklejane są wielomianowe lub kawałkami wielomianowe, tj. ich parametryzacje są opisane za pomocą wielomianów. Nakłada to spore ograniczenia na możliwe do przedstawienia w tej postaci kształty, na przykład nie istnieje wielomianowa parametryzacja okręgu. Znacznie szersze możliwości modelowania udostępniają krzywe i powierzchnie wymierne. W zasadzie każdą reprezentację krzywych wielomianowych lub kawałkami wielomianowych (sklejanych) można uogólnić tak, aby otrzymać krzywe wymierne.
Aby to zrobić, wystarczy określić krzywą (albo powierzchnię) wielomianową
w przestrzeni, której wymiar jest o ![]() większy niż wymiar przestrzeni
docelowej, tj. w przestrzeni współrzędnych
jednorodnych. Mając współrzędne np.
większy niż wymiar przestrzeni
docelowej, tj. w przestrzeni współrzędnych
jednorodnych. Mając współrzędne np. ![]() ,
, ![]() ,
, ![]() i
i ![]() punktu
punktu
![]() takiej krzywej jednorodnej, współrzędne punktu
takiej krzywej jednorodnej, współrzędne punktu ![]() krzywej wymiernej otrzymamy ze wzorów
krzywej wymiernej otrzymamy ze wzorów ![]() ,
, ![]() ,
, ![]() .
.
Krzywą ![]() w przestrzeni współrzędnych jednorodnych nazywamy
krzywą jednorodną. Pewien kłopot w jej konstruowaniu sprawia fakt,
że jeśli jest to np. krzywa Béziera, to jej punkty kontrolne
są wektorami w przestrzeni współrzędnych jednorodnych; trudno byłoby
nimi manipulować, jako że leżą w innej przestrzeni niż krzywa wymierna
(i użytkownik programu do modelowania takiej krzywej oraz obraz
krzywej utworzony przez ten program). Dlatego punkt
kontrolny (albo inne wektory w przestrzeni współrzędnych
jednorodnych, które służą do reprezentowania krzywej) najwygodniej jest
określić za pomocą punktu (albo wektora) w przestrzeni, w której
leży krzywa, oraz wagi, czyli liczbowego współczynnika dodatkowo określającego
wpływ punktu na kształt krzywej. Na przykład, jeśli przyjmiemy punkty kontrolne
w przestrzeni współrzędnych jednorodnych nazywamy
krzywą jednorodną. Pewien kłopot w jej konstruowaniu sprawia fakt,
że jeśli jest to np. krzywa Béziera, to jej punkty kontrolne
są wektorami w przestrzeni współrzędnych jednorodnych; trudno byłoby
nimi manipulować, jako że leżą w innej przestrzeni niż krzywa wymierna
(i użytkownik programu do modelowania takiej krzywej oraz obraz
krzywej utworzony przez ten program). Dlatego punkt
kontrolny (albo inne wektory w przestrzeni współrzędnych
jednorodnych, które służą do reprezentowania krzywej) najwygodniej jest
określić za pomocą punktu (albo wektora) w przestrzeni, w której
leży krzywa, oraz wagi, czyli liczbowego współczynnika dodatkowo określającego
wpływ punktu na kształt krzywej. Na przykład, jeśli przyjmiemy punkty kontrolne
![]() oraz wagi
oraz wagi ![]() , to krzywa Béziera, której
punktami kontrolnymi są wektory
, to krzywa Béziera, której
punktami kontrolnymi są wektory
![\displaystyle\bm{P}_{i}\:=\:\left[\begin{array}[]{c}w_{i}x_{i}\\
w_{i}y_{i}\\
w_{i}z_{i}\\
w_{i}\end{array}\right],](wyklady/gk1/mi/mi641.png) |
jest jednorodną reprezentacją wymiernej krzywej Béziera, danej wzorem
W podobny sposób określa się wymierne krzywe B-sklejane, a także wymierne płaty powierzchni Béziera i B-sklejane.
Wymierne krzywe i powierzchnie sklejane znane są pod nazwą NURBS, która jest skrótem angielskiego określenia non-uniform rational B-splines. Słowa non-uniform (czyli nierównomierne) dotyczą dopuszczalnych ciągów węzłów w definicji takiej krzywej — węzły te nie muszą być równoodległe.
6.5. Modelowanie powierzchni i brył
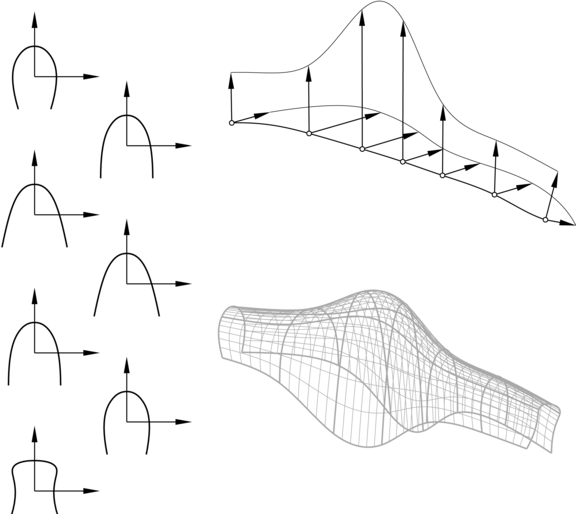
6.5.1. Zakreślanie
Zakreślanie (ang. sweeping) jest sposobem określania powierzchni, w najprostszym przypadku za pomocą krzywej, tzw. przekroju i odcinka, tzw. prowadnicy. Zasada jest przedstawiona na rysunku.
Konstrukcję tę można uogólniać na wiele sposobów; jednym z nich jest przekształcanie przekroju podczas ,,przesuwania” go wzdłuż prowadnicy. Jeśli przekształcenie to jest jednokładnością o ustalonym środku, to zamiast powierzchni walcowej otrzymujemy powierzchnię stożkową. Dalsze możliwości uogólnienia tej konstrukcji są następujące:
-
Prowadnica może być krzywą;
-
Każdemu punktowi prowadnicy odpowiada inne przekształcenie afiniczne, któremu będzie poddany przekrój;
-
Można też dopuścić zmiany kształtu przekroju podczas ,, przesuwania” go.
Dopuszczenie wszystkich tych możliwości wymaga opisania powierzchni zakreślanej wzorem
W tym wzorze występują krzywe:
-
prowadnica,
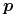 ,
,
-
tzw. kierownice,
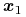 ,
, 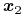 ,
, 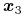 ,
, -
przekrój,
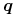 , który jest w najogólniejszym przypadku
jednoparametrową rodziną krzywych.
, który jest w najogólniejszym przypadku
jednoparametrową rodziną krzywych.
Zmienna ![]() jest parametrem przekroju; zmienna
jest parametrem przekroju; zmienna ![]() , która jest parametrem prowadnicy
i kierownic, jest też parametrem rodziny krzywych opisujących przekrój. We wzorze
są widoczne funkcje
, która jest parametrem prowadnicy
i kierownic, jest też parametrem rodziny krzywych opisujących przekrój. We wzorze
są widoczne funkcje ![]() ,
, ![]() i
i ![]() , które
opisują współrzędne punktu przekroju.
, które
opisują współrzędne punktu przekroju.
Zauważmy, że dla ustalonego ![]() wzór opisujący powierzchnię
zakreślaną opisuje przekształcenie afiniczne, którego część liniowa
jest określona przez macierz
wzór opisujący powierzchnię
zakreślaną opisuje przekształcenie afiniczne, którego część liniowa
jest określona przez macierz ![]() ,
a wektor przesunięcia jest równy
,
a wektor przesunięcia jest równy ![]() .
.
Jeśli wszystkie krzywe są krzywymi B-sklejanymi i przekrój nie zależy od
![]() , to mając łamane kontrolne tych krzywych można dość łatwo
skonstruować siatkę kontrolną powierzchni zakreślanej. W przypadku
zmieniającego się przekroju jest to trudniejsze i dlatego zwykle konstruuje
się przybliżenie takiej powierzchni. Są dwa sposoby otrzymania takiego
przybliżenia:
, to mając łamane kontrolne tych krzywych można dość łatwo
skonstruować siatkę kontrolną powierzchni zakreślanej. W przypadku
zmieniającego się przekroju jest to trudniejsze i dlatego zwykle konstruuje
się przybliżenie takiej powierzchni. Są dwa sposoby otrzymania takiego
przybliżenia:
-
Tablicujemy wzór określający powierzchnię; otrzymujemy w ten sposób prostokątną tablicę punktów na powierzchni. Na podstawie tych punktów generujemy trójkąty, które jeśli jest ich dość dużo, przybliżają powierzchnię dostatecznie dokładnie.
-
Konstruujemy powierzchnię rozpinaną. W tym celu należy wyznaczyć krzywe B-sklejane opisujące przekrój dla wybranych wartości parametru
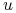 , a następnie wyznaczyć powierzchnię interpolacyjną dla tych
krzywych.
, a następnie wyznaczyć powierzchnię interpolacyjną dla tych
krzywych.
6.5.2. Powierzchnie rozpinane
Przypuśćmy, że dane są liczby (węzły) ![]() i krzywe
B-sklejane
i krzywe
B-sklejane ![]() dla
dla ![]() . Powierzchnia rozpinana
. Powierzchnia rozpinana
![]() spełnia warunek
spełnia warunek ![]() dla każdego
dla każdego ![]() .
.
Założymy, że stopień i ciąg
węzłów użyty do określenia wszystkich krzywych ![]() jest
identyczny. Punktem wyjścia do konstrukcji reprezentacji B-sklejanej
powierzchni rozpinanej jest konstrukcja B-sklejanej krzywej interpolacyjnej,
określonej przez podanie punktów
jest
identyczny. Punktem wyjścia do konstrukcji reprezentacji B-sklejanej
powierzchni rozpinanej jest konstrukcja B-sklejanej krzywej interpolacyjnej,
określonej przez podanie punktów ![]() . Mamy obliczyć punkty
kontrolne krzywej
. Mamy obliczyć punkty
kontrolne krzywej ![]() , takiej że
, takiej że ![]() ,
,
![]() .
.
Konstrukcja dla ![]() wygląda następująco: przyjmujemy
wygląda następująco: przyjmujemy ![]() ,
,
![]() . Punkty krzywej
. Punkty krzywej ![]() otrzymamy, rozwiązując
układ równań liniowych
otrzymamy, rozwiązując
układ równań liniowych
![\displaystyle\left[\begin{array}[]{@{}c@{\!}c@{\hspace{0.415cm}}c@{\:}c@{\:}c@{\:}c@{\!}c@{}}1&&&&&&\\
&1&&&&&\\
&N^{3}_{1}(u_{4})&N^{3}_{2}(u_{4})&N^{3}_{3}(u_{4})&&&\\
&&\ddots&\ddots&\ddots&&\\
&&&N^{3}_{{N-7}}(u_{{N-4}})&N^{3}_{{N-6}}(u_{{N-4}})&N^{3}_{{N-5}}(u_{{N-4}})&\\
&&&&&1&\\
&&&&&&1\end{array}\right]\left[\begin{array}[]{@{}c@{}}\bm{d}_{0}\\
\bm{d}_{1}\\
\bm{d}_{2}\\
\vdots\\
\bm{d}_{{N-6}}\\
\bm{d}_{{N-5}}\\
\bm{d}_{{N-4}}\end{array}\right]=\left[\begin{array}[]{@{}c@{}}\bm{x}_{3}\\
\bm{d}_{1}\\
\bm{x}_{4}\\
\vdots\\
\bm{x}_{{N-4}}\\
\bm{d}_{{N-5}}\\
\bm{x}_{{N-3}}\end{array}\right].](wyklady/gk1/mi/mi678.png) |
Punkty ![]() i
i ![]() można wybrać dowolnie (podanie tych
punktów określa tzw. warunki brzegowe krzywej). Współczynniki
macierzy można obliczyć ze wzorów (otrzymanych na podstawie wzoru
Mansfielda-de Boora-Coxa (6.1) i (6.2))
można wybrać dowolnie (podanie tych
punktów określa tzw. warunki brzegowe krzywej). Współczynniki
macierzy można obliczyć ze wzorów (otrzymanych na podstawie wzoru
Mansfielda-de Boora-Coxa (6.1) i (6.2))
Aby skonstruować B-sklejaną powierzchnię interpolacyjną (powierzchnię
rozpinaną), wystarczy zamiast punktów ![]() podstawić ,,punkty” —
łamane kontrolne krzywych
podstawić ,,punkty” —
łamane kontrolne krzywych ![]() . Liczba współrzędnych każdego
takiego punktu jest równa
. Liczba współrzędnych każdego
takiego punktu jest równa ![]() razy liczba punktów kontrolnych łamanej.
Obliczone ,,punkty”
razy liczba punktów kontrolnych łamanej.
Obliczone ,,punkty” ![]() w przestrzeni o tym samym wymiarze w
podobny sposób reprezentują kolumny siatki kontrolnej powierzchni
rozpinanej. Wybór kolumn numer
w przestrzeni o tym samym wymiarze w
podobny sposób reprezentują kolumny siatki kontrolnej powierzchni
rozpinanej. Wybór kolumn numer ![]() i
i ![]() , określających warunki
brzegowe, jest dowolny.
, określających warunki
brzegowe, jest dowolny.
6.5.3. Powierzchnie zadane w postaci niejawnej
Najczęściej stosowane w grafice powierzchnie zadane w postaci niejawnej to
powierzchnie algebraiczne i kawałkami algebraiczne, czyli zbiory miejsc
zerowych wielomianów trzech zmiennych. Najbardziej znana reprezentacja
płaszczyzny, za pomocą dowolnego punktu ![]() i wektora
normalnego
i wektora
normalnego ![]() , jest w istocie niejawna:
, jest w istocie niejawna:
Podobnie, współrzędne środka ![]() i promień
i promień ![]() są
współczynnikami równania sfery:
są
współczynnikami równania sfery:
Dość często spotyka się w praktyce powierzchnie wyższego stopnia (np. torus, powierzchnia stopnia ![]() ), ale rzadko stopień ten jest większy niż
kilka.
), ale rzadko stopień ten jest większy niż
kilka.
Określenie prostokątnego płata Béziera opiera się na pojęciu
iloczynu tensorowego dwóch przestrzeni funkcji jednej zmiennej. Możemy
rozpatrywać iloczyny tensorowe większej liczby przestrzeni. Jeśli są to
przestrzenie wielomianów stopnia ![]() ,
, ![]() ,
, ![]() , to bazą ich iloczynu
tensorowego jest np. baza
, to bazą ich iloczynu
tensorowego jest np. baza
Dowolny wielomian trzech zmiennych, stopnia ![]() , można przedstawić w
tej bazie. W kostce
, można przedstawić w
tej bazie. W kostce ![]() określmy punkty
określmy punkty ![]() .
Określmy wielomian
.
Określmy wielomian
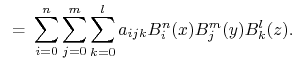 |
Współczynnik ![]() przyporządkujemy punktowi
przyporządkujemy punktowi ![]() .
Wielomian
.
Wielomian ![]() w tym punkcie kostki przyjmuje
maksymalną wartość.
w tym punkcie kostki przyjmuje
maksymalną wartość.
Powierzchnia określona za pomocą takiego wielomianu trzech zmiennych jest
zbiorem jego miejsc zerowych wewnątrz kostki. Wyznaczanie punktów takiej
powierzchni lub jej przybliżenia (np. za pomocą trójkątów) wymaga
obliczania wartości funkcji ![]() , najczęściej podczas rozwiązywania
równania nieliniowego, które powstaje przez podstawienie parametrycznej
reprezentacji pewnej prostej:
, najczęściej podczas rozwiązywania
równania nieliniowego, które powstaje przez podstawienie parametrycznej
reprezentacji pewnej prostej:
Znając rozwiązanie ![]() tego równania możemy obliczyć współrzędne
punktu na powierzchni na podstawie reprezentacji prostej.
Metody, w których jest stosowane to podejście, będą omówione później;
jedną z nich jest śledzenie promieni, a drugą to metoda
maszerujących sześcianów. Zwróćmy uwagę, że na ogół nie warto
wyznaczać współczynników wielomianu
tego równania możemy obliczyć współrzędne
punktu na powierzchni na podstawie reprezentacji prostej.
Metody, w których jest stosowane to podejście, będą omówione później;
jedną z nich jest śledzenie promieni, a drugą to metoda
maszerujących sześcianów. Zwróćmy uwagę, że na ogół nie warto
wyznaczać współczynników wielomianu ![]() zmiennej
zmiennej ![]() , który występuje
po lewej stronie równania. Stopień tego wielomianu jest równy
, który występuje
po lewej stronie równania. Stopień tego wielomianu jest równy ![]() ,
czyli jest duży. Zamiast tego, wygodniej jest obliczać wartość
wielomianu
,
czyli jest duży. Zamiast tego, wygodniej jest obliczać wartość
wielomianu ![]() sposobem podobnym do wyznaczania punktu płata Béziera.
Mamy
sposobem podobnym do wyznaczania punktu płata Béziera.
Mamy
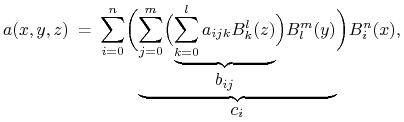 |
co umożliwia zastosowanie algorytmu de Casteljau albo schematu Hornera.
Algorytm de Casteljau umożliwia podział kostki, w której jest określona
powierzchnia, na prostopadłościany. Możemy to wykorzystać do otrzymania
obszaru o dowolnie małej objętości, w którym znajduje się powierzchnia.
Wystarczy dzielić rekurencyjnie kostkę i odrzucać te jej fragmenty,
w których współczynniki lokalnej reprezentacji wielomianu ![]() mają stały
znak. To jest oczywiście zastosowanie własności otoczki wypukłej
opisanej tu reprezentacji wielomianu trzech zmiennych.
mają stały
znak. To jest oczywiście zastosowanie własności otoczki wypukłej
opisanej tu reprezentacji wielomianu trzech zmiennych.
W grafice komputerowej bardzo popularne są powierzchnie określane słowem blob
(to angielskie słowo nie doczekało się polskiego odpowiednika). Powierzchnia taka może być
zbiorem miejsc zerowych funkcji ![]() określonej wzorami
określonej wzorami
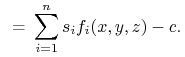 |
Zamiast funkcji przestępnej ![]() często do określenia blobu wykorzystuje się też wielomiany.
często do określenia blobu wykorzystuje się też wielomiany.
Aby określić taką powierzchnię, należy określić tzw. szkielet, czyli
zbiór punktów ![]() oraz parametry
oraz parametry ![]() i
i ![]() dla każdego
z tych punktów i współczynnik
dla każdego
z tych punktów i współczynnik ![]() . Zbiór rozwiązań równania
. Zbiór rozwiązań równania
![]() jest wprawdzie sferą, ale jeśli punktów szkieletu jest
więcej niż
jest wprawdzie sferą, ale jeśli punktów szkieletu jest
więcej niż ![]() , to otrzymujemy gładkie połączenia nieco zdeformowanych
sfer. Zwiększanie parametru
, to otrzymujemy gładkie połączenia nieco zdeformowanych
sfer. Zwiększanie parametru ![]() powoduje powiększanie sfery (lub ,,rozdmuchiwanie”
odpowiedniego fragmentu powierzchni), zaś parametr
powoduje powiększanie sfery (lub ,,rozdmuchiwanie”
odpowiedniego fragmentu powierzchni), zaś parametr ![]() odpowiada za
długość gradientu funkcji
odpowiada za
długość gradientu funkcji ![]() ; im większy, tym ,,sztywniejsza” jest
powierzchnia ze względu na zmiany parametru
; im większy, tym ,,sztywniejsza” jest
powierzchnia ze względu na zmiany parametru ![]() . Na lewym
rysunku 6.21 jest pokazana taka powierzchnia razem z trzema
kulami, których środki tworzą jej szkielet, z prawej zaś strony są trzy
takie powierzchnie, które różnią się tylko wartościami parametru
. Na lewym
rysunku 6.21 jest pokazana taka powierzchnia razem z trzema
kulami, których środki tworzą jej szkielet, z prawej zaś strony są trzy
takie powierzchnie, które różnią się tylko wartościami parametru ![]() .
.
Powierzchnie zadane w sposób niejawny mają to do siebie, że funkcja
występująca w definicji umożliwia rozróżnienie trzech podzbiorów
przestrzeni: powierzchnia jest zbiorem miejsc zerowych. W punktach
należących do wnętrza bryły, której brzegiem jest rozpatrywana
powierzchnia, funkcja ma wartości dodatnie, a punkty na zewnątrz
odpowiadają ujemnym wartościom funkcji (można też traktować znaki
funkcji odwrotnie). Ta informacja jest niesłychanie ważna podczas
znajdowania punktów powierzchni, a także w konstrukcyjnej geometrii brył
i dlatego nie należy uważać funkcji ![]() albo
albo ![]() za
pełnowartościową reprezentację powierzchni, mimo że funkcje te mają
zbiór miejsc zerowych taki sam jak funkcja
za
pełnowartościową reprezentację powierzchni, mimo że funkcje te mają
zbiór miejsc zerowych taki sam jak funkcja ![]() .
.