Zagadnienia
7. Reprezentacje scen trójwymiarowych
7.1. Prymitywy i obiekty złożone
Obiekty trójwymiarowe dzielimy na
-
obiekty z zamkniętą objętością (bryły),
-
obiekty z otwartą objętością (powierzchnie, krzywe),
-
są też obiekty specjalne, np. chmury, płomienie lub futro, reprezentowane przez pola skalarne lub wektorowe, których wygląd na obrazach powinien ukazywać ich budowę przestrzenną.
Obiekt z zamkniętą objętością jest zwykle wizualizowany przez narysowanie obrazu powierzchni stanowiącej jego brzeg. Dlatego często są one reprezentowane za pomocą powierzchni brzegowej (spotykany skrót B-rep oznacza reprezentację bryły za pomocą brzegu). Od obiektów z otwartą objętością bryły odróżniają się tym, że nie można ,,obejrzeć” obu stron powierzchni takiej figury bez przeniknięcia przez nią.
Oprócz podziału podanego wyżej, obiekty można klasyfikować według sposobu ich określenia i reprezentowania. Obiekt, który jest określony za pomocą innych obiektów (np. stanowiących jego części) jest to tzw. obiekt złożony. Obiekt określony bez odwoływania się do innych, prostszych obiektów to tzw. prymityw7W tym określeniu nie ma niczego pejoratywnego.. Te określenia nie są zbyt precyzyjne, ponieważ uznanie obiektu za złożony lub za prymityw zależy od zastosowania, a nawet kontekstu. Na przykład za prymityw możemy uznać wielościan opisany za pomocą list wierzchołków, krawędzi i ścian, jeśli figur tych nie rozpatrujemy w oderwaniu od wielościanu. Natomiast z punktu widzenia OpenGL-a prymitywem geometrycznym jest tylko punkt, odcinek lub wielokąt wypukły, który można narysować bezpośrednio.
Jest oczywiste, że reprezentacja obiektu może być inna dla potrzeb wykonywania obrazu niż dla potrzeb przetwarzania danych. Na przykład wyświetlenie obrazu powierzchni złożonej z wielu płatów B-sklejanych polega na wyznaczeniu dostatecznie dużej liczby dostatecznie małych trójkątów, które są następnie rzutowane, rasteryzowane i teksturowane. W tym przypadku odpowiednią reprezentacją powierzchni jest zbiór trójkątów. Natomiast interakcyjne kształtowanie takiej powierzchni (np. w systemie CAD) polega na dobieraniu węzłów i punktów kontrolnych, przy czym spełnienie warunków nałożonych na płaty (takich jak gładkość połączeń na wspólnych brzegach) może być zapewnione przez użycie specjalnej struktury danych, której najprostszą częścią są tablice węzłów i punktów kontrolnych płatów. Zaryzykowałbym stwierdzenie, że zaprojektowanie takiej struktury danych jest najtrudniejszym zadaniem do rozwiązania podczas tworzenia programów.
7.2. Reprezentowanie brył wielościennych
Przypomnijmy, że
-
Brzeg bryły wielościennej jest zbiorem płaskich wielokątów, tzw. ścian.
-
Brzeg ściany jest zbiorem odcinków, tzw. krawędzi.
-
Brzeg krawędzi składa się z dwóch punktów, tzw. wierzchołków.
Widać tu pewną hierarchię, oraz analogie między poszczególnymi poziomami tej hierarchii. Reprezentacja bryły może składać się z tablicy punktów, krawędzi i ścian; każda z tych tablic może zawierać odnośniki do pozostałych tablic.
Reprezentacja punktu w przestrzeni trójwymiarowej zawiera
oczywiście ![]() współrzędne kartezjańskie lub
współrzędne kartezjańskie lub ![]() jednorodne.
Może ona także zawierać listę (indeksów
do tablicy) krawędzi, których końcem jest dany punkt oraz listę
(indeksów do tablicy) ścian, dla których dany punkt jest wierzchołkiem.
Dodatkowymi informacjami związanymi z punktem są np. wektor
normalny,
potrzebny w obliczeniach oświetlenia i w cieniowaniu powierzchni,
współrzędne tego punktu w przestrzeni tekstury i inne.
jednorodne.
Może ona także zawierać listę (indeksów
do tablicy) krawędzi, których końcem jest dany punkt oraz listę
(indeksów do tablicy) ścian, dla których dany punkt jest wierzchołkiem.
Dodatkowymi informacjami związanymi z punktem są np. wektor
normalny,
potrzebny w obliczeniach oświetlenia i w cieniowaniu powierzchni,
współrzędne tego punktu w przestrzeni tekstury i inne.
Reprezentacja krawędzi najczęściej zawiera wskaźniki (indeksy) punktów końcowych i wskaźniki ścian, których dana krawędź jest wspólnym brzegiem. Reprezentacja krawędzi może też zawierać informację, czy na obrazie krawędź ta ma być wygładzona (jeśli gładka powierzchnia krzywoliniowa jest przybliżana przez powierzchnię złożoną z trójkątów, to raczej tego chcemy).
Zamiast krawędzi wygodne może być używanie półkrawędzi: krawędź wspólna dwóch ścian jest reprezentowana za pomocą dwóch półkrawędzi, z których każda jest częścią reprezentacji jednej z tych ścian. Każda półkrawędź ma wskaźnik do drugiej półkrawędzi. Zaletą takiej reprezentacji jest uproszczenie implementacji różnych algorytmów.
Reprezentacja ściany może zawierać listę krawędzi, albo listę list krawędzi (ta ostatnia reprezentacja przydaje się, jeśli ściana nie jest spójna lub jednospójna). Może też zawierać listę wierzchołków, a także obie listy: krawędzi i wierzchołków. Aby przyspieszyć wyświetlanie ściany, można ją podzielić na trójkąty (albo dokonać innego wygodnego podziału; np. biblioteka GL w standardzie OpenGL, której procedury bezpośrednio współpracują ze sprzętem, umożliwia wyświetlanie tylko wielokątów wypukłych). Lista tych trójkątów w reprezentacji ściany może znacznie przyspieszyć wykonywanie obrazu.
Zyski czasowe z utworzenia takich list trójkątów należy rozpatrywać w dwojakim kontekście. Po pierwsze, w programie interakcyjnym (takim jak system CAD albo gra komputerowa), ta sama ściana bywa wyświetlana wielokrotnie, np. z różnych punktów położenia obserwatora. Biblioteka GLU w OpenGL-u umożliwia wyświetlanie wielokątów niewypukłych, jednak wtedy ta sama praca (dzielenia wielokąta na wypukłe kawałki) jest wykonywana wielokrotnie8Chyba, że posługujemy się listami obrazowymi OpenGL-a. Jeśli takich ścian jest dużo, to częstość odświeżania obrazu (podczas animacji w czasie rzeczywistym) może zmniejszyć się, znacznie obniżając komfort pracy użytkownika programu. Po drugie, programy wykonujące obraz fotorealistyczny, np. metodą śledzenia promieni lub bilansu energetycznego, muszą obliczać przecięcia promieni (pewnych półprostych w przestrzeni) ze ścianami. Zastąpienie skomplikowanych ścian odpowiednimi listami trójkątów może przyspieszyć działanie programu o kilka procent, co przy czasie obliczeń rzędu minut lub nawet godzin też ma znaczenie.
Dodatkowe możliwe atrybuty ściany, to wektor normalny (zwróćmy uwagę, że wektor normalny może być też związany z wierzchołkami ściany), reprezentacja układu odniesienia współrzędnych tekstury, identyfikator rodzaju powierzchni i jej własności optyczne (przezroczystość, współczynnik załamania światła, kolor itd.).
Jak widać, taka reprezentacja zawiera sporo informacji redundantnej. Jest to spowodowane przez
-
potrzebę używania takiej informacji bez wielokrotnego wyznaczania jej na podstawie minimalnego zbioru danych wystarczającego do tego,
-
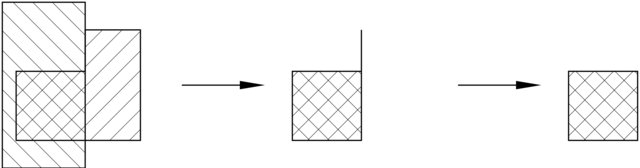
potrzebę sprawdzania poprawności; na przykład, dla bryły, której powierzchnia jest homeomorficzna ze sferą, prosty test poprawności polega na sprawdzeniu wzoru Eulera:
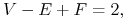
w którym
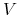 oznacza liczbę wierzchołków,
oznacza liczbę wierzchołków, 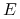 — krawędzi, a
— krawędzi, a 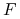 —
ścian. Informacja redundantna może zarówno ułatwić, jak i utrudnić
sprawdzanie poprawności danych, które jest konieczne zwłaszcza podczas
wymiany danych między różnymi programami.
—
ścian. Informacja redundantna może zarówno ułatwić, jak i utrudnić
sprawdzanie poprawności danych, które jest konieczne zwłaszcza podczas
wymiany danych między różnymi programami.
Przykład: Rozwiązanie przyjęte w moim pakiecie BSTools reprezentuje siatkę, która może opisywać brzeg wielościanu, a także powierzchnię siatkową (zobacz p. LABEL:ssect:siatki) za pomocą sześciu tablic. Zdefiniowane są następujące struktury w C:
typedef struct {
char degree, tag;
int firsthalfedge;
} BSMfacet, BSMvertex;
typedef struct {
int v0, v1;
int facetnum;
int otherhalf;
} BSMhalfedge;
Pierwsza struktura reprezentuje ściany i wierzchołki, dlatego ma dwie nazwy. Mamy dwie
tablice takich struktur, elementy jednej reprezentują ściany, a drugiej wierzchołki.
Pole degree, tj. stopień, oznacza liczbę (pół)krawędzi (i wierzchołków) ściany
albo liczbę półkrawędzi wychodzących z danego wierzchołka. W dodatkowych dwóch tablicach
liczb całkowitych przechowuje się indeksy półkrawędzi — dzięki takiemu rozwiązaniu
nie ma ciasnego ograniczenia stopni ścian i wierzchołków i nie marnuje się miejsca.
Długość tych tablic jest równa liczbie półkrawędzi, która jest sumą stopni wszystkich
wierzchołków i sumą stopni wszystkich ścian. Pole firsthalfedge struktury
BSMfacet lub BSMvertex oznacza indeks pierwszej półkrawędzi dla danej ściany
lub wierzchołka. Pole tag jest używane przez różne procedury przetwarzania siatek.
Piąta tablica, struktur BSMhalfedge, reprezentuje półkrawędzie.
Półkrawędź jest opisana przez podanie indeksów wierzchołków v0 i v1,
indeksu ściany facetnum, do której brzegu należy półkrawędź i indeksu
otherhalf drugiej półkrawędzi o tych samych wierzchołkach końcowych (ale
o przeciwnej orientacji). Jeśli krawędź jest brzegowa, to pole otherhalf
ma wartość ![]() .
.
Szósta tablica służy do przechowywania współrzędnych poszczególnych wierzchołków. Dzięki rozdzieleniu informacji topologicznej na temat wierzchołka od jego współrzędnych, te same struktury mogą opisywać siatki płaskie i przestrzenne, a także można podawać współrzędne jednorodne. W dodatkowych tablicach, zależnie od potrzeb, można przechowywać wektory normalne dla ścian lub wierzchołków, współrzędne tekstury, kolory itd.
Opisana wyżej reprezentacja wielościanu stanowi pewnego rodzaju ,,program maksimum”. Bywa ona potrzebna w niektórych algorytmach widoczności i w konstrukcyjnej geometrii brył, ale często wiele jej elementów jest zbędnych. Dla kontrastu, przypomnijmy ,,minimalną” reprezentację powierzchni wielościennej, stosowaną w komunikacji między programem a sprzętem, jaką jest taśma trójkątowa, czyli ciąg punktów, w którym każde trzy kolejne punkty są wierzchołkami trójkąta.
7.3. Konstrukcyjna geometria brył
Obiekty, które definiujemy ,,w jednym kawałku”, są nazywane prymitywami; mogą to być np. wielościany, albo bryły, których brzegiem jest powierzchnia algebraiczna. Z tych obiektów można budować obiekty bardziej złożone, przy czym zwykle dodawanie obiektów nie wystarczy. Czasem interesuje nas bryła, która jest różnicą (mnogościową) brył danych; jeśli chcemy np. pograć w bilard, to trzeba usunąć kawałki stołu (wywiercić otwory na bile).
W zasadzie konstrukcyjna geometria brył (ang. constructive solid geometry, CSG9Nie będziemy wprowadzali skrótu polskiej nazwy.) jest zastosowaniem algebry zbiorów. Mając do dyspozycji prymitywy i bryły z nich zbudowane, można określić ich sumę, przecięcie, różnicę i dopełnienie. Bryła o skomplikowanym kształcie jest opisana przez pewne wyrażenie mnogościowe, które wygodnie jest przedstawić w postaci drzewa (tzw. drzewa CSG).
Słowa ,,w zasadzie” oznaczają pewne dodatkowe przekształcenie, jakiemu jest poddawany wynik każdej operacji mnogościowej. Jest nim tzw. regularyzacja. Zbiór regularny jest domknięciem swojego wnętrza. Brzeg takiego zbioru należy do niego i w otoczeniu każdego punktu brzegu leżą punkty z wnętrza — a zatem np. każda ściana wielościanu regularnego może być widoczna z jednej strony (czyli, powtarzając wcześniejsze uwagi, bryły CSG są obiektami o zamkniętej objętości).
Niezależnie od algorytmów wyznaczania reprezentacji brył CSG, określenie takich brył jest źródłem kłopotów, spowodowanych błędami zaokrągleń (małe zaburzenia argumentów mogą istotnie zmienić wynik operacji). Ponadto nawet dla bryły wielościennej znalezienie reprezentacji brzegu jest skomplikowane z powodu mnóstwa kłopotliwych przypadków szczególnych, które algorytm rozwiązujący to zadanie musi uwzględniać. Mimo to często wyznacza się reprezentację wielościennych brył CSG, ponieważ jest to jedyna reprezentacja, która może posłużyć do utworzenia obrazu za pomocą wydajnych i powszechnie dostępnych algorytmów widoczności. W przypadku brył ograniczonych powierzchniami algebraicznymi albo stosuje się przybliżenie tych powierzchni złożone z trójkątów (i wtedy można stosować algorytmy tworzenia obrazu odpowiednie dla wielościanów), albo też jedyną reprezentacją bryły CSG jest samo drzewo CSG; niektóre algorytmy widoczności (algorytm śledzenia promieni i odpowiednie warianty algorytmu przeglądania liniami poziomymi) są w stanie utworzyć obraz bryły CSG bez wyznaczania jawnej reprezentacji brzegu tej bryły.
7.3.1. Wyznaczanie przecięcia wielościanów
Mając dwa wielościany reprezentowane za pomocą ich brzegów (czyli listy wierzchołków, krawędzi i ścian), możemy wyznaczyć brzeg wielościanu, który jest ich regularyzowanym przecięciem. Przypuśćmy, że reprezentacja ma tę własność, że dla każdej ściany wektor normalny jest zorientowany ,,na zewnątrz” bryły. Aby wyznaczyć jej dopełnienie, wystarczy zmienić zwrot wektora normalnego każdej ściany na przeciwny. Operacje wyznaczania przecięcia i dopełnienia umożliwiają otrzymanie sumy i różnicy brył.
Aby znaleźć brzeg wielościanu, który jest regularyzowanym przecięciem dwóch regularnych wielościanów o znanych brzegach, można wykonać algorytm naszkicowany niżej:
-
Dla każdej pary ścian, z których jedna jest częścią brzegu jednej, a druga częścią brzegu drugiej bryły, wyznaczamy przecięcia tych ścian. Przecięcie to może być zbiorem pustym, punktem, odcinkiem lub wielokątem. Jeśli przecięcie ścian jest wielokątem, to znajdujemy odcinki będące przecięciami krawędzi jednej ściany z drugą (to wymaga obcinania odcinka do wielokąta w ogólności niewypukłego).
-
Odcinkami wyznaczonymi w poprzednim kroku dzielimy ściany wielokątów na spójne fragmenty. Wnętrze każdego takiego fragmentu ściany bryły w całości leży wewnątrz drugiej bryły, na zewnątrz, lub na jej brzegu. Określamy graf sąsiedztwa fragmentów ścian, którego wierzchołkami są fragmenty, a krawędziami są krawędzie wielościanów lub odcinki otrzymane w pierwszym kroku.
-
Wybieramy nieodwiedzony fragment ściany (wierzchołek grafu sąsiedztwa ścian) i sprawdzamy (np. na podstawie reguły parzystości), czy należy on do brzegu przecięcia brył.
-
Metodą DFS lub (lepiej) BFS przeszukujemy graf sąsiedztwa ścian, przy czym na krawędzi przecięcia zatrzymujemy przeszukiwanie. Jeśli fragment ściany, od którego zaczęliśmy przeszukiwanie, należy do przecięcia, to wszystkie odwiedzone fragmenty też. Fragmenty takie dołączamy do reprezentacji przecięcia brył, a pozostałe (nie należące do przecięcia) zaznaczamy jako odwiedzone.
Kroki
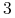 i
i 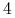 powtarzamy tak długo, aż zostaną odwiedzone wszystkie
fragmenty ścian brył wyjściowych.
powtarzamy tak długo, aż zostaną odwiedzone wszystkie
fragmenty ścian brył wyjściowych. -
Wynikiem przeszukiwania jest reprezentacja brzegu przecięcia brył w postaci grafu sąsiedztwa ścian, w którym brakuje krawędzi przecięcia ścian znalezionych w pierwszym kroku). Krawędzie te dołączamy teraz do grafu.
Dzielenie ścian na fragmenty można uzupełnić o triangulację lub o podział na fragmenty wypukłe, dzięki czemu będziemy mieli dane o postaci ułatwiającej dalsze ich przetwarzanie (np. wykonywanie dalszych operacji CSG, albo wyświetlanie). Procedura opisana wyżej jest dość prosta (choć niektóre jej fragmenty są nietrywialne), jednak największy kłopot polega na uodpornieniu jej na szczególne przypadki danych, np. taki jak na rysunku 7.4.
Opisana wyżej procedura jest potrzebna, jeśli obrazy brył CSG mamy otrzymywać za pomocą algorytmów widoczności, które wymagają jawnej reprezentacji brzegu (np. w postaci listy wielokątów do wyświetlenia). Takim algorytmem jest np. algorytm z buforem głębokości. Istnieją jednak algorytmy widoczności dopuszczające opis brył CSG w postaci reprezentacji prymitywów i drzew CSG (np. można zrealizować w ten sposób śledzenie promieni). Co więcej, taki opis jest jedynym możliwym ,,dokładnym” opisem wielu brył CSG utworzonych z prymitywów będących bryłami krzywoliniowymi. Aby wyświetlić taką bryłę za pomocą algorytmu z buforem głębokości, trzeba najpierw znaleźć wielościany będące przybliżeniami prymitywów, a następnie wielościany reprezentujące bryłę CSG.
7.4. Drzewa i grafy scen
Ważną cechą scen trójwymiarowych, która powinna być uwzględniona w reprezentacji, jest hierarchia obiektów. Zwykle nie określa się sceny jako liniowej listy prymitywów do wyświetlenia, ale raczej komponuje się ją z obiektów, z których każdy jest złożony z jeszcze prostszych obiektów itd. Prymitywy są na samym dole tej hierarchii.
Opisana wyżej hierarchia może być odzwierciedlona za pomocą drzewa hierarchii sceny. Korzeń drzewa reprezentuje całą scenę. Każdy wierzchołek drzewa reprezentuje pewien prymityw lub wskazuje wierzchołki będące korzeniami swoich poddrzew (np. zawiera wskaźnik początku listy tych wierzchołków). Ponadto każdy wierzchołek zawiera dodatkowe atrybuty, które są elementami określenia sceny, albo są potrzebne do usprawnienia procesu wykonywania obrazu. Atrybuty mogą być następujące:
-
Przekształcenie geometryczne. Opisuje ono przejście między układem współrzędnych związanym z wierzchołkiem drzewa położonym wyżej w hierarchii, a układem, w którym jest określony obiekt reprezentowany przez wierzchołek dany. Na przykład jeśli reprezentowana scena jest umeblowanym pomieszczeniem, to każdy mebel jest opisany w pewnym swoim układzie, a jego przekształcenie określa ustawienie go w pomieszczeniu. Wazon stojący na stole lub książki na półce mają przekształcenia opisujące ich ustawienie względem odpowiedniego mebla.
Najczęściej przekształcenie obiektu jest afiniczne lub rzutowe, a jego reprezentacją w wierzchołku drzewa hierarchii jest odpowiednia macierz.
-
Bryła otaczająca. Może nią być prostopadłościan o krawędziach równoległych do osi lokalnego układu współrzędnych (wówczas wystarczy podać sześć liczb; zwróćmy uwagę, że zwykle łatwo jest je znaleźć, np. dla powierzchni Béziera wystarczy znaleźć najmniejsze i największe współrzędne punktów kontrolnych). Bryła taka umożliwia pominięcie czasochłonnego przetwarzania poddrzewa, jeśli program wykryje, że jest ona w całości niewidoczna (np. zasłonięta przez inny obiekt). Inne zastosowanie brył otaczających, które może znacznie skrócić czas obliczeń, to wykrywanie kolizji obiektów w animacji.
-
Uproszczona reprezentacja obiektu. Jeśli obiekt na obrazie jest mały (co można zbadać wyznaczając rzut bryły otaczającej), to nie należy tracić czasu na rysowanie go ze wszystkimi szczegółami. Można narysować nawet bardzo uproszczony obraz, np. odpowiednio poteksturowany prostopadłościan zamiast domu, samochodu lub drzewa w rozległym pejzażu, co oczywiście zajmie mniej czasu niż rysowanie wszystkich dachówek, wentyli w kołach lub liści, które trzeba by narysować na obrazie danego obiektu widzianego z bliska.
Rysowanie uproszczonych obiektów, jeśli są one małe na obrazie, nazywa się elizją. Termin ten pochodzi z językoznawstwa i oznacza zanikanie pewnych głosek w płynnej mowie, czyli w pewnym sensie pomijanie mało istotnych szczegółów wymawianych słów (co nie ma niczego wspólnego z niestaranną wymową).
-
Działanie CSG. Konstrukcyjna geometria brył w naturalny sposób wiąże się z hierarchicznym opisem sceny. Możemy zatem zrealizować jednolitą hierarchiczną reprezentację sceny z bryłami CSG. Oczywiście, albo algorytm tworzenia obrazu takiej sceny musi dopuszczać takie dane, albo też reprezentacja musi zostać poddana wstępnemu przetwarzaniu, w wyniku którego powstanie reprezentacja nadająca się do wyświetlenia sceny za pomocą algorytmu, który ma być użyty.
Często zdarza się, że pewne obiekty pojawiają się w scenie ,,w wielu egzemplarzach”. Na przykład samochody mają najczęściej cztery jednakowe koła. Byłoby rzeczą niestosowną każde z kół opisywać osobno, a jeszcze bardziej niestosowne byłoby tworzenie osobnych reprezentacji wszystkich szprych w tych kołach. Dlatego zamiast drzewa bardziej odpowiednią strukturą danych reprezentującą hierarchię sceny bywa bezcyklowy graf skierowany (ang. directed acyclic graph, DAG). Podobnie jak drzewo ma on korzeń, tj. wierzchołek od którego zaczyna się przeszukiwanie grafu, ale do niektórych wierzchołków można dojść od korzenia na więcej niż jeden sposób. Każdy wierzchołek ma określony poziom, który określimy jako długość najdłuższej drogi od korzenia do tego wierzchołka (w drzewie jest to długość jedynej drogi). Każdy wierzchołek bezcyklowego grafu skierowanego ma poziom skończony, co oznacza, że w grafie nie ma cykli, tj. nie można, idąc wzdłuż krawędzi zgodnie z ich orientacją, dojść ponownie do wierzchołka, z którego się wyszło. Krawędzie takiego grafu określają częściowy porządek wierzchołków; idąc wzdłuż krawędzi zgodnie z ich orientacją, przechodzimy przez wierzchołki o coraz większych poziomach. Wierzchołki, z których nie wychodzą żadne krawędzie, podobnie jak w drzewie, nazywamy liśćmi.
Wyświetlenie sceny reprezentowanej przez bezcyklowy graf skierowany można wykonać tak samo jak wyświetlanie sceny reprezentowanej przez drzewo; należy przeszukać graf metodą DFS (oczywiście nie zaznaczając odwiedzonych wierzchołków). W związku z tym, że pewne obiekty mogą być wyświetlane wielokrotnie, listę atrybutów wierzchołków można rozszerzyć o atrybuty modyfikujące interpretację poddrzew. Na przykład możemy mieć scenę, w której jest kilka jednakowych samochodów pomalowanych na różne kolory. Graf będzie zawierał opis tylko jednego samochodu, ale kolor jego karoserii (nie opon!) będzie ustalony na drodze od korzenia całego grafu do korzenia podgrafu reprezentującego samochód (podobnie jak przekształcenie określające położenie tego samochodu). Można wprowadzić wiele parametrów modyfikujących, na przykład kąt skręcenia przednich kół, uchylenia drzwi, itd.
Na rysunku 7.5 jest przedstawiony obraz (inspirowany jedną
z grafik M. C. Eschera) sceny złożonej
z ![]() kul i
kul i ![]() walców. Bezcyklowy graf skierowany
reprezentujący tę scenę miał
walców. Bezcyklowy graf skierowany
reprezentujący tę scenę miał ![]() wierzchołki, przy czym wszystkie
wierzchołki oprócz korzenia i liści miały wskaźniki do dwóch
wierzchołków o większym poziomie.
wierzchołki, przy czym wszystkie
wierzchołki oprócz korzenia i liści miały wskaźniki do dwóch
wierzchołków o większym poziomie.