Zagadnienia
1. Wprowadzenie
1.1. Wstęp i podstawowe pojęcia
Inżynieria finansowa to dyscyplina, która zajmuje się analizą właściwości instrumentów finansowych, w szczególności instrumentów pochodnych.
Instrument pochodny![]() to instrument finansowy (kontrakt,
umowa), którego wartość wypłaty (wypłat) zależy od wartości, które
przyjmą (lub przyjęły) w określonych umową chwilach czasu inne
instrumenty finansowe. O instrumentach finansowych, od wartości
których zależy wypłata (zależą wypłaty) instrumentu pochodnego
to instrument finansowy (kontrakt,
umowa), którego wartość wypłaty (wypłat) zależy od wartości, które
przyjmą (lub przyjęły) w określonych umową chwilach czasu inne
instrumenty finansowe. O instrumentach finansowych, od wartości
których zależy wypłata (zależą wypłaty) instrumentu pochodnego ![]() ,
mówimy że są tak zwanymi instrumentami podstawowymi instrumentu
pochodnego (ang. underlyings). W szczególności, instrumentem
podstawowym instrumentu pochodnego może być inny instrument
pochodny.
,
mówimy że są tak zwanymi instrumentami podstawowymi instrumentu
pochodnego (ang. underlyings). W szczególności, instrumentem
podstawowym instrumentu pochodnego może być inny instrument
pochodny.
1.2. Zasadnicze kategorie instrumentów pochodnych
Kontrakty forward
-
FX forward
-
FX swap
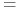 FX spot
FX spot  FX forward
FX forward -
terminowy zakup/sprzedaż obligacji
-
transakcje repo (buy sell back) i reverse repo (sell buy back) na papierach wartościowych
Kontrakty futures
-
futures na obligacje skarbowe
-
futures na stopę procentową (Eurodollar futures)
-
futures na indeksy/akcje
-
futures na towary
Kontrakty wymiany stóp procentowych
-
FRA – Forward Rate Agreement
-
OIS – OverNight Indexed Swap
-
IRS – Interest Rate Swap
-
CCIRS – Cross Currency Interest Rate Swap
Kontrakty opcyjne
-
opcje walutowe (waniliowe, azjatyckie, barierowe, binarne)
-
opcje na stopę procentową (cap/floor)
-
opcje na kontrakt IRS (swapcje)
-
opcje na obligacje
-
opcje na indeksy/akcje
-
opcje na towary
Kontrakty wymiany cen towarów
Kredytowe instrumenty pochodne
-
opcje na default
-
swap default-owy – credit default swap (CDS)
Instrumenty powstałe w drodze sekurytyzacji (długu)
-
obligacje MBS – Mortgage Backed Securities
-
obligacje CMO – Collateralized Mortgage Obligations
-
obligacje CDO – Collateralized Debt Obligations
Kilka przykładów wypłat opcyjnych instrumentów pochodnych (opcji)
Uwaga: Szczegółowe charakterystyki tych instrumentów będą podane na przyszłych wykładach.
-
europejska opcja kupna
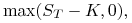
gdzie
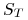 jest wartością akcji w chwili
zapadalności opcji
jest wartością akcji w chwili
zapadalności opcji  , a
, a  jest ceną wykonania (dlaczego
instrument o takiej wypłacie nazywamy opcją?)
jest ceną wykonania (dlaczego
instrument o takiej wypłacie nazywamy opcją?) -
europejska opcja kupna na średnią arytmetyczną (opcja azjatycka o europejskim typie wykonania)
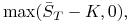
gdzie
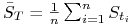 przy czym
przy czym 
-
europejska opcja kupna akcji droższej z dwóch
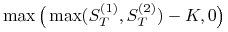
-
europejska opcja wymiany akcji A na akcję B
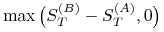
-
europejska binarna opcja kupna (sprzedaży)
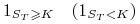
-
europejska barierowa opcja kupna typu up-and-out
![\max(S_{T}-K,0)\, 1_{{\{\max _{{t\in[0,T]}}S_{t}<H\}}},](wyklady/ifi/mi/mi29.png)
gdzie
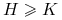 jest tak zwaną barierą.
jest tak zwaną barierą.
Uwagi
-
Wypłaty opcji 1), 3), 4) i 5) zależą tylko od wartości instrumentów podstawowych w chwili zapadalności opcji – o takich opcjach mówimy że nie zależą od ,,drogi” (trajektorii procesu cen instrumentów podstawowych).
-
W opcjach 3) i 4) mamy dwa instrumenty podstawowe.
-
Wypłaty opcji 2) i 6) zależą od ,,drogi” instrumentu podstawowego, każda na swój specyficzny sposób.
-
Wypłaty opcji 5) są funkcjami nieciągłymi ceny instrumentu podstawowego w chwili zapadalności opcji. Zarządzanie ryzykiem opcji o nieciągłych wypłatach jest zdecydowanie trudniejsze niż w przypadku opcji których wypłaty są ciągłe.
Głównymi celami inżynierii finansowej są:
wycena instrumentów pochodnych
-
wycena z modelu – ang. mark-to-model, którą stosuje się, gdy nie jest możliwa
-
wycena do rynku – ang. mark-to-market.
konstrukcja strategii zabezpieczających instrumenty pochodne,
analiza i pomiar ryzyka instrumentów pochodnych,
konstrukcje złożonych strukturalnych produktów finansowych dopasowanych do potrzeb rynku.
1.3. Rynki finansowe
Rynki finansowe to świat (miejsce), w którym żyją (na którym są handlowane) instrumenty finansowe. Rynki finansowe dzielą się na segmenty, które odpowiadają różnym aspektom instrumentów finansowych na nich handlowanych oraz podmiotom dopuszczonym do handlu. I tak na przykład mamy
-
Rynek kapitałowy (papiery wartościowe, akcje)
-
Rynek pieniężny (kasowy) – instrumenty dłużne (lokaty/depozyty, bony, obligacje)
-
Rynek instrumentów pochodnych
-
Rynek walutowy – transakcje wymiany walut
Rynki możemy też podzielić na:
Rynki regulowane – giełdy
-
produkty wystandaryzowane
-
z systemami zabezpieczeń mającymi wyeliminować ryzyko kredytowe (rozliczeniowe i przedrozliczeniowe transakcji)
Rynki pozagiełdowe – klientowskie, OTC (Over The Counter)
-
rynek międzybankowy (instytucji finansowych)
-
rynek dużych wiarygodnych klientów (korporacji)
Bieżący obraz statystyczny rynków finansowych
Na podstawie danych opracowanych przez Bank for International Settlements (Bazylea) – patrz Triennial Central Bank Survey of Foreign Exchange and Derivatives Market Activity in April 2007; Preliminary global results; September 2007 (opracowanie dostępne na stronie http://www.bis.org).
![]() Struktura rynków OTC instrumentów pochodnych
ze względu na rodzaj czynnika ryzyka instrumentu podstawowego.
Struktura rynków OTC instrumentów pochodnych
ze względu na rodzaj czynnika ryzyka instrumentu podstawowego.
Tabela poniżej przedstawia strukturę tych rynków w dwóch ujęciach - udziały procentowe nominałów (Nominał) oraz udziały procentowe wartości (Wartość) niezapadłych (na koniec grudnia 2006) transakcji na tych instrumentach na rynku OTC.
| Rodzaj ryzyka | Nominał | Wartość |
| Stopy procentowe | 70.3 | 49.9 |
| Kursy wymiany walut | 9.7 | 13.0 |
| Akcje/Indeksy | 1.8 | 8.8 |
| Ryzyko kredytowe (CDS) | 6.9 | 4.8 |
| Towary | 1.7 | 6.9 |
| Inne | 9.6 | 16.6 |
Jak widać z powyższej tabeli najważniejszymi czynnikami są stopy procentowe oraz kursy wymiany walut. Dlatego poniżej skoncentrujemy się głównie na pochodnych których instrumentami podstawowymi są czynniki ryzyka z tych grup.
Dane są prezentowane dla dwóch segmentów rynków finansowych
Rynek walutowy – tradycyjne transakcje wymiany walut
-
transakcje FX spot
-
transakcje FX forward
-
transakcje FX swap
Rynek OTC instrumentów pochodnych:
-
pochodne kursów walutowych, głównie
-
walutowe kontrakty wymiany procentowej (CCIRS)
-
opcje walutowe (waniliowe i egzotyczne)
-
-
pochodne stopy procentowej, głównie
-
kontrakty na przyszłą stopę procentową (FRA)
-
kontrakty wymiany procentowej (IRS)
-
opcje na stopę procentową (waniliowe i egzotyczne)
-
![]() Średni dzienny obrót na rynkach:
walutowym oraz pochodnych OTC
Średni dzienny obrót na rynkach:
walutowym oraz pochodnych OTC
| Instrument | 2001 | 2004 | 2007 |
| FX spot | 387 | ||
| FX fwd | 131 | ||
| FX swap | 656 | ||
| Total – FX | 1200 | ||
| CCIRS | 7 | ||
| Opcje walutowe | 60 | ||
| Inne | 0 | 2 | 0 |
| Total – Pochodne walutowe | 67 | ||
| FRA | 129 | ||
| IRS | 331 | ||
| Opcje na stopę | 29 | ||
| Total – Pochodne stopy | 489 |
![]() Udziały walut na rynku walutowym
Udziały walut na rynku walutowym
| Waluta | 2001 | 2004 | 2007 |
|---|---|---|---|
| USD | 90.3 | 88.7 | 86.3 |
| EUR | 37.6 | 37.2 | 37.0 |
| JPY | 22.7 | 20.3 | 16.5 |
| GBP | 13.2 | 16.9 | 15.0 |
| PLN | 0.5 | 0.4 | 0.8 |
Symbole walut: PLN – Złoty Polski, EUR – Euro, USD – dolar USA,
GBP – funt brytyjski, JPY – jen japoński. Ponieważ w każdej
transakcji wymiany walutowej biorą udział dwie waluty, udziały (po
wszystkich walutach) powinny sumować się do ![]() .
.
![]() Udziały par walutowych (kursów wymiany)
na rynku walutowym
Udziały par walutowych (kursów wymiany)
na rynku walutowym
| Kurs wymiany | 2001 | 2004 | 2007 |
| USD/EUR | 30 | 28 | 27 |
| USD/JPY | 20 | 17 | 13 |
| USD/GBP | 11 | 14 | 12 |
| USD/CHF | 5 | 4 | 5 |
| USD/CAD | 4 | 4 | 4 |
| USD/AUD | 4 | 5 | 6 |
| USD/Inne | 17 | 16 | 19 |
| EUR/JPY | 3 | 3 | 2 |
| EUR/GBP | 2 | 2 | 2 |
![]() Główne centra obrotu na rynku
tradycyjnych transakcji walutowych (FX), na rynku pochodnych OTC
oraz dane dla Polski dla tych segmentów rynku
Główne centra obrotu na rynku
tradycyjnych transakcji walutowych (FX), na rynku pochodnych OTC
oraz dane dla Polski dla tych segmentów rynku
Tabela poniżej przedstawia geograficzną strukturę aktywności rynków tradycyjnych transakcji wymiany walut (FX spot, FX fwd, FX swap oznaczonych w tabeli symbolem FX) i rynku pochodnych OTC.
| Kraj | FX | OTC |
| Wielka Brytania | 34.1 | 42.5 |
| Stany Zjednoczone | 16.6 | 23.8 |
| Japonia | 6.0 | 3.5 |
| Singapur | 5.8 | 2.7 |
| Niemcy | 2.5 | 3.7 |
| Irlandia | 0.3 | 3.4 |
| Hong Kong | 4.4 | 0.9 |
| Szwajcaria | 6.1 | 2.9 |
| Australia | 4.2 | 1.2 |
| Francja | 3.0 | 7.2 |
| Polska | 0.2 | 0.1 |
1.4. Zmienne rynkowe – ceny
Podstawowe zmienne rynkowe, które często pełnią role instrumentów podstawowych instrumentów pochodnych
-
ceny akcji spółek giełdowych, wartości indeksów giełdowych,
-
kursy wymiany walut,
-
stopy procentowe (depozytowe, kontraktów IRS, referencyjne (typu LIBOR), etc.),
-
ceny obligacji,
-
kontrakty futures,
-
ceny towarów (surowce, metale, ropa, produkty rolne, etc.).
Wartość instrumentów pochodnych staramy się wyrazić jako funkcje
-
wartości instrumentów podstawowych (cen spot – to jest cen ,,natychmiastowej” dostawy) lub struktury cen forward),
-
bieżącej struktury stóp procentowych,
-
zmienności instrumentów podstawowych, a w niektórych przypadkach i korelacji między nimi.
Zmienne rynkowe są opisywane (modelowane) matematycznie przez procesy stochastyczne o odpowiednich właściwościach. Na przykład niech
-
 oznacza proces ceny akcji spółki giełdowej,
oznacza proces ceny akcji spółki giełdowej, -
w chwili bieżącej
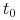 obserwujemy na rynku cenę
obserwujemy na rynku cenę 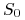 , która jest
realizacją zmiennej losowej
, która jest
realizacją zmiennej losowej 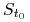 ,
, -
dla przyszłych chwil czasu
 , tj. dla
, tj. dla 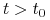 ,
, 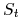 jest zmienną
losową.
jest zmienną
losową.
Często będziemy postulować, że proces stochastyczny opisujący zmienną rynkową spełnia pewne stochastyczne równanie (na szczęście na ogół dość proste), na przykład
gdzie ![]() ,
, ![]() są pewnymi stałymi (liczbami
rzeczywistymi), a
są pewnymi stałymi (liczbami
rzeczywistymi), a ![]() jest tzw. procesem Wienera (o tym więcej
później).
jest tzw. procesem Wienera (o tym więcej
później).
Uwaga: Równanie tego typu służy do wyprowadzenia formuły na wycenę instrumentu pochodnego. Natomiast nie jest ono używane do prognozowania przyszłych wartości zmiennej rynkowej.
Rodzaje cen instrumentów finansowych
-
transakcyjne – odzwierciedlają rzeczywisty stan rynku
-
kwotowane – bardziej odzwierciedlają oczekiwania rynku, lub też zamiary kwotującego w stosunku do własnego portfela
-
fixingi, kursy zamknięcia – oficjalne ceny odniesienia, często stosowane przy rozliczaniu transakcji, na ogół są średnimi cen kwotowanych – np. kursy walutowe NBP fixing, stopy WIBOR, LIBOR – ustalane przez odpowiednie niezależne organizacje.
Ceny mają strony, mianowicie
-
cena kupna (ile skłonny jest zapłacić kwotujący) – BID Price,
-
cena sprzedaży (za ile kwotujący jest skłonny sprzedać) – OFFER Price,
-
cena średnia – MID Price.
Oczywiście musi zachodzić relacja
cena kupna ![]() cena sprzedaży.
cena sprzedaży.
Uwagi:
-
Ceny natychmiastowe (spotowe) to ceny dla transakcji zawartych w chwili bieżącej i rozliczanych lub w ramach których dostawa nastąpi natychmiast, przy czym to co znaczy natychmiast zależy od zasad przyjętych na danym rynku (z uwzględnieniem specyfiki waluty).
-
Cena instrumentu finansowego nie zawsze jest tożsama z sumą pieniędzy, którą trzeba zapłacić za ten instrument. Będziemy rozróżniać między ceną instrumentu a jego wartością, czyli kwotą pieniędzy, którą trzeba za dany instrument zapłacić.
Ceny akcji, wartości indeksów
Akcje
-
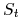 – cena za 1 akcję, wyrażona w walucie lokalnej, w chwili
– cena za 1 akcję, wyrażona w walucie lokalnej, w chwili  ,
, -
dostawa natychmiastowa
 dostawa i jej rozliczenie
następuje w tym samym dniu kiedy zawarto transakcję kupna
(sprzedaży), konwencja
dostawa i jej rozliczenie
następuje w tym samym dniu kiedy zawarto transakcję kupna
(sprzedaży), konwencja 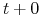
-
akcje na ogół płacą dywidendę, zwykle raz lub dwa razy w roku,
-
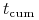 – ostatni dzień, w którym kupujący akcję nabiera prawa do
najbliższej dywidendy,
– ostatni dzień, w którym kupujący akcję nabiera prawa do
najbliższej dywidendy, -
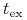 – pierwszy dzień, w którym kupujący akcję nie otrzymuje
prawa do najbliższej dywidendy,
– pierwszy dzień, w którym kupujący akcję nie otrzymuje
prawa do najbliższej dywidendy, -
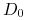 – wartość bieżąca (na dzień cum-dividend) najbliższej dywidendy,
– wartość bieżąca (na dzień cum-dividend) najbliższej dywidendy, -
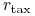 – stopa podatku od przychodów z inwestycji kapitałowych,
– stopa podatku od przychodów z inwestycji kapitałowych, -
jeśli inne czynniki nie wpływałyby na cenę akcji, musiałoby zachodzić
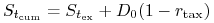
tak więc następuje deterministyczna ale skokowa zmiana (spadek) ceny akcji.
-
czasami akcje są poddawane podziałowi (ang. split) na
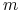 części, wtedy w dniu splitu
części, wtedy w dniu splitu 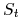 zostaje zastąpione przez
zostaje zastąpione przez 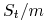 .
.
Indeksy
-
Są w pewnym przybliżeniu syntetycznym portfelem wybranej grupy spółek giełdowych
-
Odzwierciedlają stan i zmiany wartości portfela spółek wchodzących w jego skład
-
Indeks możemy traktować jak syntetyczną spółkę, z tym że nie można dostarczyć fizycznie akcji tej syntetycznej spółki.
-
Indeksy ,,płacą” dywidendę w sposób ciągły, a nie w sposób dyskretny tak jak zwykłe akcje.
Kursy wymiany walut
ang. FX rate (Foreign eXchange rate)
-
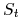 – wartość kursu natychmiastowej
wymiany waluty
– wartość kursu natychmiastowej
wymiany waluty 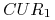 na
na 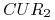 w chwili
w chwili 
-
wymiana natychmiastowa (ang. FX spot)
 wymiana
(dostawa, rozliczenie) następuje w dniu spot, to jest
(zwykle) za 2 dni handlowe od
wymiana
(dostawa, rozliczenie) następuje w dniu spot, to jest
(zwykle) za 2 dni handlowe od  , konwencja
, konwencja 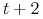
-
wymiana walut
 jedną walutę kupujemy, a drugą sprzedajemy
jedną walutę kupujemy, a drugą sprzedajemy -
kurs wymiany można podawać na dwa sposoby:
-
jako ilość waluty
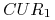 za jednostkę waluty
za jednostkę waluty
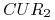

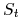
-
jako ilość waluty
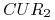 za jednostkę waluty
za jednostkę waluty 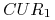

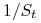
-
-
waluta bazowa
 w odniesieniu do kwotowanego
kursu ta waluta za jednostkę, której podajemy ilość drugiej waluty
w odniesieniu do kwotowanego
kursu ta waluta za jednostkę, której podajemy ilość drugiej waluty -
waluta niebazowa, kwotowana
 ta druga waluta, w tej walucie
wyrażamy wartość jednostki waluty bazowej
ta druga waluta, w tej walucie
wyrażamy wartość jednostki waluty bazowej -
notacja:
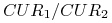 , gdzie
, gdzie 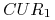 – waluta bazowa, a
– waluta bazowa, a
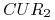 – waluta niebazowa, i zwykle (ang. direct quotation)
oznacza ilość waluty
– waluta niebazowa, i zwykle (ang. direct quotation)
oznacza ilość waluty 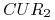 za jednostkę waluty
za jednostkę waluty 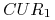 (odwrotnie
niż się oznacza miana w fizyce!); zdarza się jednak, że pod takim
oznaczeniem kryje się kwotowanie odwrotne (ang. indirect
quotation) – ilość waluty
(odwrotnie
niż się oznacza miana w fizyce!); zdarza się jednak, że pod takim
oznaczeniem kryje się kwotowanie odwrotne (ang. indirect
quotation) – ilość waluty 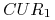 za jednostkę waluty
za jednostkę waluty 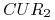 -
tak na przykład jest kwotowany kurs funta brytyjskiego GBP do dolara
amerykańskiego USD – wtedy USD/GBP oznacza ilość USD za 1 GBP.
Dlatego dobrze jest się upewnić jak kwotowany jest kurs, nim się
zacznie go używać.
-
tak na przykład jest kwotowany kurs funta brytyjskiego GBP do dolara
amerykańskiego USD – wtedy USD/GBP oznacza ilość USD za 1 GBP.
Dlatego dobrze jest się upewnić jak kwotowany jest kurs, nim się
zacznie go używać. -
w danym kraju podaje się głównie kursy walut obcych do waluty lokalnej
-
kurs krosowy
 kurs między dwoma obcymi walutami,
musi w stosunku do waluty lokalnej (np. PLN) spełniać warunek
kurs między dwoma obcymi walutami,
musi w stosunku do waluty lokalnej (np. PLN) spełniać warunek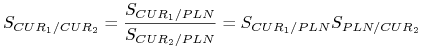
-
Warunek ten wynika z założenia braku arbitrażu na lokalnym rynku walutowym
-
Cena kupna (BID Price) – ale którą walutę ,,kupujemy”? Reguła ,,trzech B” (Buy, Base, Bid) – kupujemy (Buy) walutę bazową (Base) po cenie BID (tej niższej)
-
Przykład: nasze kwotowanie
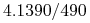 USD/PLN oznacza, że jesteśmy
gotowi kupić USD po
USD/PLN oznacza, że jesteśmy
gotowi kupić USD po 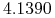 PLN za
PLN za 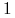 USD, lub sprzedać USD po
USD, lub sprzedać USD po
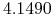 PLN za
PLN za 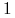 USD.
USD. -
Ta zasada jest spójna z zasadami kwotowania cen kupna/sprzedaży akcji – w powyższym przykładzie USD ,,gra rolę akcji”.
Zagadnienia i zadania na Ćwiczenia
Ćwiczenie 1.1 (Wycena pozycji a wynik na tej pozycji na przykładzie portfela akcji)
Dealer Banku Miejskiego utworzył
portfel akcji spółki wuwu.com w następujący sposób:
-
w poniedziałek kupił 200 akcji po 10 PLN,
-
we wtorek dokupił 300 akcji po 9 PLN,
-
w środę kupił jeszcze 500 akcji po 9.50 PLN.
Od czwartku zaczął stopniowo zamykać pozycję:
-
we czwartek sprzedał 300 akcji po 9.75 PLN,
-
w piątek sprzedał 400 akcji po 10.25 PLN.
Wyceń portfel tych akcji oraz oblicz wynik na tym portfelu
-
(a) we czwartek,
-
(b) w piątek.
Wynik podziel na wynik zrealizowany i wynik niezrealizowany. Licząc wynik zastosuj
-
(i) kolejkę FIFO (ang. First In First Out),
-
(ii) metodę średniej ceny.
Portfel akcji był finansowany (ang. cost of carry) stopą ON (ang. Over Night), która wynosiła
-
w poniedziałek –
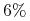 ,
,
-
we wtorek –
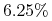 ,
, -
we środę –
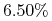 ,
, -
we czwartek –
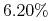 ,
, -
w piątek –
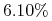 .
.
Skoryguj wynik na tym portfelu o koszty finansowania pozycji.
Uwagi i wyjaśnienia:
-
W metodzie średniej ceny wynik liczony jest względem średniej ceny akcji w portfelu wyliczonej dla dnia realizacji zysku/straty.
-
Koszt finansowania pozycji z dany dzień to odsetki od kwoty ,,pożyczonych” funduszy użytych dla otwarcia pozycji, zbilansowanych wpływami z zamkniętych części portfela, i uwzględniających narosłe do danego dnia koszty finansowania. Koszty finansowania nalicza się na bazie dziennej.
Ćwiczenie 1.2 (Portfel bonów skarbowych)
Dealer Banku Miejskiego otworzył portfel bonów skarbowych kupując bony o wartości nominalnej 10 mln PLN po cenie 85. W chwili otwarcia portfela termin wykupu bonów przypadał za 100 dni. Po 10 dniach dealer dokupił 5 mln PLN bonów tej samej emisji po cenie 86. Po kolejnych 20 dniach zamknął część pozycji sprzedając bony o wartości nominalnej 12 mln PLN po cenie 90, po czym założył że będzie trzymał pozostałą pozycję aż do wykupu bonów.
-
(a) Wyceń ten portfel na 50 dni przed terminem wykupu, kiedy cena bonów wynosiła 92.
-
(b) Oblicz wynik na tym portfelu i podziel go na wynik zrealizowany i niezrealizowany.
-
(c) Oblicz koszt finansowania portfela przy założeniu, że stopa ON używana do naliczania kosztów finansowania była stała w tym okresie i wynosiła 5%.
Wyjaśnienie: Wynik zrealizowany na papierze dyskontowym (np. na
bonie skarbowym) kupionym po cenie ![]() wynosi
wynosi
gdzie ![]() jest wartością nominalną papieru,
jest wartością nominalną papieru, ![]() jest liczbą dni od
daty dostawy dla daty zakupu papieru do daty dostawy dla daty
wyceny, a
jest liczbą dni od
daty dostawy dla daty zakupu papieru do daty dostawy dla daty
wyceny, a ![]() jest liczbą dni od daty dostawy dla daty
zakupu papieru do daty zapadalności papieru. Takie określenie wyniku
zrealizowanego jest zabiegiem księgowym i służy tylko do ,,wygodnej
dla księgowych” prezentacji wyniku i w zasadzie nie ma nic
wspólnego z rzeczywistą realizacją zysku/straty. Z tego powodu wynik
zrealizowany z tytułu rozliczenia dyskonta nie jest uwzględniany
przy wyliczaniu kosztu finansowania pozycji.
jest liczbą dni od daty dostawy dla daty
zakupu papieru do daty zapadalności papieru. Takie określenie wyniku
zrealizowanego jest zabiegiem księgowym i służy tylko do ,,wygodnej
dla księgowych” prezentacji wyniku i w zasadzie nie ma nic
wspólnego z rzeczywistą realizacją zysku/straty. Z tego powodu wynik
zrealizowany z tytułu rozliczenia dyskonta nie jest uwzględniany
przy wyliczaniu kosztu finansowania pozycji.
Ćwiczenie 1.3 (Portfel obligacji)
Dealer Banku Miejskiego
kupił obligacje o wartości nominalnej 100 mln PLN. W chwili zawarcia
transakcji rezydualny termin do wykupu tych obligacji wynosił 2 lata
i 3 miesiące licząc od daty dostawy. Obligacje płacą kupon ![]() (semi-annual, 30/360). Cena czysta obligacji wynosiła 95. Po 4
miesiącach dealer sprzedał 40 mln PLN z tego portfela kiedy cena
czysta obligacji wynosiła 96. Oblicz wynik na tym portfelu i podziel
go na wynik zrealizowany i wynik niezrealizowany. Oblicz koszty
finansowania portfela przy założeniu, że stopa ON była stała w
rozpatrywanym okresie i wynosiła
(semi-annual, 30/360). Cena czysta obligacji wynosiła 95. Po 4
miesiącach dealer sprzedał 40 mln PLN z tego portfela kiedy cena
czysta obligacji wynosiła 96. Oblicz wynik na tym portfelu i podziel
go na wynik zrealizowany i wynik niezrealizowany. Oblicz koszty
finansowania portfela przy założeniu, że stopa ON była stała w
rozpatrywanym okresie i wynosiła ![]() .
.
Wyjaśnienie: Do wyniku zrealizowanego na obligacji kuponowej, prócz
rozliczenia dyskonta lub premii (analogicznie jak w przypadku bonów;
jest to znów zabieg księgowy!), zalicza się otrzymane kupony oraz
narosłe odsetki ![]() za bieżący okres odsetkowy (ang. accrued
interest). Narosłe odsetki
za bieżący okres odsetkowy (ang. accrued
interest). Narosłe odsetki ![]() oblicza się następującym wzorem
oblicza się następującym wzorem
gdzie ![]() oznacza wartość
najbliższego kuponu,
oznacza wartość
najbliższego kuponu, ![]() liczbę dni w bieżącym okresie
odsetkowym, a
liczbę dni w bieżącym okresie
odsetkowym, a ![]() liczbę dni od początku okresu odsetkowego do daty
rozliczenia (dostawy) dla bieżącego dnia.
liczbę dni od początku okresu odsetkowego do daty
rozliczenia (dostawy) dla bieżącego dnia.
Ćwiczenie 1.4 (Przykład złożonego instrumentu finansowego (Lokata schodkowa))
Bank oferuje klientom lokatę na następujących warunkach:
-
walutą lokaty jest waluta obca CUR (klient deponuje ustaloną sumę pieniędzy w tej walucie
-
oprocentowanie lokaty jest następujące
-
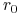 jeśli
jeśli 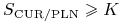 , przy czym
zwrot kapitału i odsetek odbędzie się w PLN przeliczonych po kursie
, przy czym
zwrot kapitału i odsetek odbędzie się w PLN przeliczonych po kursie

-
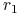 jeśli
jeśli 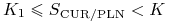
-
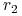 jeśli
jeśli 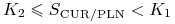
-
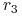 jeśli
jeśli 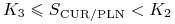
-
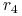 jeśli
jeśli 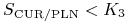
przy czym w przypadku
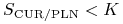 wypłata następuje w
oryginalnej walucie lokaty oraz
wypłata następuje w
oryginalnej walucie lokaty oraz 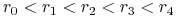
-
-
kursem referencyjnym jest fixing NBP z dnia zakończenia lokaty
Zidentyfikuj opcje wbudowane w strukturę tego instrumentu.
Ćwiczenie 1.5 (Lokata z wbudowaną opcją)
Bank oferuje klientom lokatę na następujących warunkach:
-
walutą lokaty jest PLN,
-
czas trwania lokaty wynosi
 ,
, -
odsetki z lokaty wynoszą
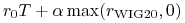 gdzie
gdzie
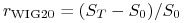 jest stopą zwrotu z indeksu WIG20 w
okresie od rozpoczęcia lokaty do chwili jej zakończenia (
jest stopą zwrotu z indeksu WIG20 w
okresie od rozpoczęcia lokaty do chwili jej zakończenia (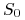 oznacza wartość indeksu z chwili rozpoczęcia lokaty, a
oznacza wartość indeksu z chwili rozpoczęcia lokaty, a 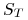 wartością indeksu z chwili zakończenia lokaty), a
wartością indeksu z chwili zakończenia lokaty), a 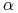 jest tak
zwanym współczynnikiem partycypacji.
jest tak
zwanym współczynnikiem partycypacji.
-
(a) Zidentyfikuj opcję wbudowaną w ten instrument.
-
(b) Wyznacz wartość współczynnika partycypacji
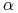 przy następujących
danych liczbowych
przy następujących
danych liczbowych-
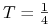 (lokata trzymiesięczna)
(lokata trzymiesięczna) -
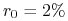
-
stopa procentowa dla trzymiesięcznych lokat wynosi
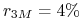
-
wartość indeksu WIG20 w chwili rozpoczęcia lokaty wynosi
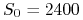
-
cena trzymiesięcznej opcji kupna na WIG20 z ceną wykonania
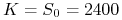 wynosi 60 (w jednostkach indeksu)
wynosi 60 (w jednostkach indeksu)
przy którym lokata będzie zawarta na ,,sprawiedliwych” warunkach.
-
-
(c) Ile kontraktów opcyjnych powinien kupić Bank by zabezpieczyć wypłatę części odsetek zależną od wartości indeksu WIG20 dla lokaty o nominale
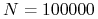 PLN.
PLN.
Uwaga: Nominał kontraktu opcyjnego na WIG20 wynosi 10, to znaczy
jest to opcja na 10 sztuk indeksu. Jednostka indeksu jest warta 10
PLN (można powiedzieć, że indeks WIG20 wynoszący ![]() (jednostek
indeksowych, punktów) jest ,,akcją” o wartości
(jednostek
indeksowych, punktów) jest ,,akcją” o wartości ![]() PLN). Zatem
wartość gotówkowa wypłaty jednego kontraktu opcyjnego kupna indeksu
wynosi
PLN). Zatem
wartość gotówkowa wypłaty jednego kontraktu opcyjnego kupna indeksu
wynosi ![]() PLN, gdzie
PLN, gdzie ![]() jest ceną
wykonania. Cena kontraktu opcyjnego na WIG20 jest podawana w
jednostkach indeksowych za jedną sztukę indeksu. Tak więc cena
gotówkowa jednego kontraktu opcyjnego, którego kwotowana cena wynosi
jest ceną
wykonania. Cena kontraktu opcyjnego na WIG20 jest podawana w
jednostkach indeksowych za jedną sztukę indeksu. Tak więc cena
gotówkowa jednego kontraktu opcyjnego, którego kwotowana cena wynosi
![]() (jednostek indeksowych), wynosi
(jednostek indeksowych), wynosi ![]() PLN.
PLN.
Ćwiczenie 1.6 (Widełki kupna/sprzedaży dla kursu krosowego)
W dniu 5 października 2004 około godziny 15:40 Bank X kwotował
-
GBP/PLN – 6.2538 / 6.2598
-
CHF/PLN – 2.7751 / 2.7791
-
(a) Oblicz kursy kupna/sprzedaży GBP/CHF, które powinien zakwotować Bank X w tym czasie.
-
(b) Przypuśćmy, że w tym samym czasie kwotowanie Banku Y kursu GBP/CHF wynosiło 2.2520 / 2.2580. Czy i w jaki sposób można było tę sytuację wykorzystać by uzyskać wolny od ryzyka dochód.
Ćwiczenie 1.7 (Kredyt hipoteczny)
Utwórz schemat spłat kredytu
hipotecznego w którym ,,równe” raty, na które składają się odsetki
i spłata kapitału, są płacone co miesiąc przez 10 lat. Jeśli kredyt
jest udzielony na stopę stałą, raty są rzeczywiście równe. Jeśli
kredyt jest udzielony na stopę zmienną (powiększoną o marżę), raty
będą się zmieniały wraz ze zmianą stopy zmiennej. Oblicz jak zmieni
się rata takiego kredytu jeśli stopa zmienna wzrośnie o 1 punkt
procentowy. Załóż że bieżąca stopa zmienna wynosi ![]() a marża
banku
a marża
banku ![]() .
.




