Zagadnienia
- 10.1 Współczynniki wrażliwości instrumentów pochodnych
- 10.2 Współczynniki wrażliwości opcji waniliowych
- 10.3 Równanie Blacka-Scholesa (związek między tetą, deltą i gammą)
- 10.4 Współczynniki wrażliwości portfela instrumentów pochodnych
- 10.5 Obliczanie współczynników wrażliwości metodą ilorazu różnicowego
- 10.6 Zabezpieczanie portfela instrumentów pochodnych
- 10.7 Dynamiczne zabezpieczanie portfela instrumentów pochodnych
- Zagadnienia i zadania na Ćwiczenia
10. Analiza wrażliwości
Analiza wrażliwości instrumentu pochodnego (portfela instrumentów pochodnych zależnych od tego samego instrumentu podstawowego) polega na analizowaniu zmian wartości instrumentu (portfela) następujących w skutek zmian wartości zmiennych będących argumentami funkcji wyceniającej instrument (portfel) na podstawie obserwacji kilku pochodnych tej funkcji względem odpowiednich zmiennych. W uproszczeniu, można powiedzieć, że jest to próba zastosowania wzoru Taylora (dla funkcji wielu zmiennych) do oszacowania zmiany wartości instrumentu (portfela). Ponadto, z informacji o wartościach współczynników wrażliwości oraz kierunku i wielkości zmian tych współczynników pod wpływem zmian argumentów funkcji wyceniającej instrument (portfel) wynikają dla zarządzającego instrumentem (portfelem) istotne wskazówki co do sposobu potencjalnego zabezpieczania instrumentu (portfela).
Analizę wrażliwości omówimy szczegółowo dla waniliowych opcji europejskich korzystając z rezultatów otrzymanych w modelu Blacka-Scholesa, bowiem w tym przypadku funkcje wyceniające opcje są dane w postaci analitycznych wyrażeń. Natomiast w przypadku portfeli instrumentów pochodnych przedstawimy jedynie ogólne zasady takiej analizy.
Niech
| (10.1) |
oznacza funkcję, która określa wartość instrumentu pochodnego. Argumentami tej funkcji są
-
 – chwila czasu w której wyznaczamy
wartość instrumentu pochodnego,
– chwila czasu w której wyznaczamy
wartość instrumentu pochodnego, -
 – wartość instrumentu podstawowego w chwili
– wartość instrumentu podstawowego w chwili  ,
, -
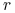 – wolna od ryzyka stopa procentowa,
– wolna od ryzyka stopa procentowa,
oraz parametry związane z przyjętym modelem opisującym proces cen instrumentu podstawowego – w przypadku prostych modeli typu Blacka-Scholesa, są to
-
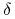 – stopa dochodu generowanego przez instrument podstawowy
(stopa dywidendy),
– stopa dochodu generowanego przez instrument podstawowy
(stopa dywidendy), -
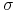 – zmienność instrumentu podstawowego.
– zmienność instrumentu podstawowego.
Funkcja ![]() na ogół zależy jeszcze od innych parametrów
charakteryzujących instrumenty pochodne, na przykład od
na ogół zależy jeszcze od innych parametrów
charakteryzujących instrumenty pochodne, na przykład od
-
terminów zapadalności
 ,
,
oraz, w szczególności,
-
dla opcji waniliowych, od cen wykonania
 ,
, -
a dla opcji barierowych, dodatkowo i od barier
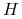 .
.
Nie będziemy analizować zależności ![]() od tych parametrów ponieważ
nie są one wielkościami zmiennymi (są ustalone w kontrakcie, nie są
czynnikami ryzyka).
od tych parametrów ponieważ
nie są one wielkościami zmiennymi (są ustalone w kontrakcie, nie są
czynnikami ryzyka).
10.1. Współczynniki wrażliwości instrumentów pochodnych
Załóżmy, że funkcja ![]() jest dostatecznie
gładka. Wówczas, zmianę wartości funkcji
jest dostatecznie
gładka. Wówczas, zmianę wartości funkcji ![]()
która następuje przy zmianie
-
ceny instrumentu podstawowego
 o wielkość
o wielkość 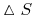 ,
, -
stopy procentowej
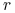 o wielkość
o wielkość 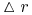 ,
, -
stopy dywidendy
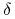 o wielkość
o wielkość 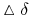 ,
, -
zmienności
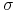 o wielkość
o wielkość 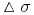
oraz na skutek
-
upływu czasu o okres
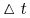 ,
,
możemy przybliżyć w następujący sposób
| (10.2) |
gdzie wszystkie pochodne są obliczane dla bieżących wartości
argumentów funkcji ![]() w chwili
w chwili ![]() . W inżynierii finansowej te
pochodne oznacza się zwykle symbolami greckich liter (za wyjątkiem
pochodnej po zmienności
. W inżynierii finansowej te
pochodne oznacza się zwykle symbolami greckich liter (za wyjątkiem
pochodnej po zmienności ![]() ). I tak mamy:
). I tak mamy:
-
deltę:
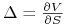
-
gammę:
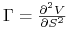
-
vegę:
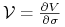 (Vega nie jest literą
greckiego alfabetu)
(Vega nie jest literą
greckiego alfabetu) -
rho:
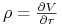
-
rho
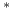 :
: 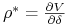
-
tetę:
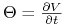
Przy tych oznaczeniach wzór (10.2) przybiera następującą postać
| (10.3) |
Zarządzający portfelem, prócz informacji o bieżącej wrażliwości
instrumentów finansowych w portfelu, czyli o wartościach
współczynników wrażliwości ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() , oraz
, oraz ![]() , powinien analizować jak wartości tych
współczynników zmienią się gdy zmienią się wartości instrumentu
podstawowego, zmienności, oraz stóp procentowych. W przypadku
portfeli instrumentów pochodnych na kurs walutowy lub na ceny
akcji/indeksy giełdowe, dla których największy wpływ na zmianę
wartości tych portfeli mają zmiany wartości instrumentu podstawowego
oraz zmiany zmienności tego instrumentu, analizuje się współczynniki
wrażliwości które są pierwszymi pochodnymi
, powinien analizować jak wartości tych
współczynników zmienią się gdy zmienią się wartości instrumentu
podstawowego, zmienności, oraz stóp procentowych. W przypadku
portfeli instrumentów pochodnych na kurs walutowy lub na ceny
akcji/indeksy giełdowe, dla których największy wpływ na zmianę
wartości tych portfeli mają zmiany wartości instrumentu podstawowego
oraz zmiany zmienności tego instrumentu, analizuje się współczynniki
wrażliwości które są pierwszymi pochodnymi ![]() ,
, ![]() oraz
oraz
![]() po
po ![]() i po
i po ![]() . W szczególności obserwuje się
następujące pochodne
. W szczególności obserwuje się
następujące pochodne
-
vannę:
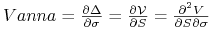
-
volgę:
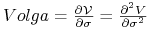
-
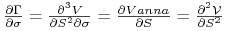
-
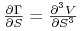
Uwaga 10.1
Dla instrumentów pochodnych stopy procentowej odpowiednikiem Delty jest BPV. W przypadku takiego instrumentu Deltę możemy określić jako pochodną funkcji
gdzie ![]() jest funkcją wyceniającą
ten instrument, względem przesunięcia równoległego
jest funkcją wyceniającą
ten instrument, względem przesunięcia równoległego ![]() bieżącej krzywej stóp procentowych
bieżącej krzywej stóp procentowych ![]()
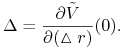 |
Wówczas związek pomiędzy Deltą a BPV jest następujący
Deltę możemy również powiązać z duracją ![]() instrumentu, mianowicie mamy następujący związek
instrumentu, mianowicie mamy następujący związek
Analogicznie, jeśli zdefiniować Gammę instrumentu pochodnego stopy procentowej jako drugą pochodną
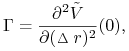 |
to
gdzie ![]() jest tak zwaną wypukłością tego
instrumentu.
jest tak zwaną wypukłością tego
instrumentu.
10.2. Współczynniki wrażliwości opcji waniliowych
W przypadku opcji waniliowych wycenianych formułami Blacka-Scholesa możemy wypisać analityczne wyrażenia na te pochodne.
Delta
Korzystając z formuł (9.32) – (9.33) na wartość opcji kupna / sprzedaży otrzymujemy następujące wyrażenia na
deltę opcji kupna:
| (10.4) |
deltę opcji sprzedaży
| (10.5) |
gdzie, przypomnijmy,
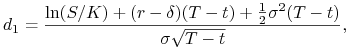 |
a ![]() jest dystrybuantą standardowego
rozkładu normalnego.
jest dystrybuantą standardowego
rozkładu normalnego.
Wzór na deltę opcji sprzedaży (10.5) można również wyprowadzić z wyrażenia (10.4) na deltę opcji kupna i związku między tymi deltami, który wynika z parytetu opcji kupna-sprzedaży. Oczywiście, są to delty kupionych opcji (długich pozycji w tych opcjach).
Własności delt
-
Delta mierzy wrażliwość (pierwszego rzędu) ceny opcji na zmianę wartości instrumentu podstawowego.
-
Delta opcji kupna / sprzedaży ATM (to jest gdy
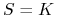 ) wynosi w przybliżeniu
) wynosi w przybliżeniu 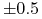 .
Czasami opcje ATM
definiuje się jako opcje z ceną wykonania
.
Czasami opcje ATM
definiuje się jako opcje z ceną wykonania  taką by delta tej
opcji wynosiła dokładnie
taką by delta tej
opcji wynosiła dokładnie 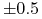 .
. -
Funkcje
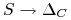 oraz
oraz 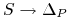 są ściśle
rosnące (bo gamma, która jest pochodną delt jest dodatnia).
są ściśle
rosnące (bo gamma, która jest pochodną delt jest dodatnia). -
Delta opcji, jako funkcja
 , zmienia się najszybciej w otoczeniu ceny wykonania, a więc dla
opcji
które są (niemal) ATM – patrz własności gammy.
, zmienia się najszybciej w otoczeniu ceny wykonania, a więc dla
opcji
które są (niemal) ATM – patrz własności gammy. -
Przy
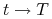
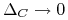 gdy
gdy 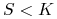 oraz
oraz
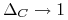 gdy
gdy 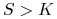 . Natomiast, dla opcji sprzedaży
. Natomiast, dla opcji sprzedaży
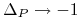 gdy
gdy 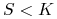 oraz
oraz 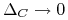 gdy
gdy
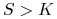 .
.
Uwaga 10.2
W praktyce rynkowej funkcjonuje również pojęcie forward delty, która jest zdefiniowana wzorem
gdzie ![]() dla opcji kupna i
dla opcji kupna i ![]() dla opcji
sprzedaży. Jednocześnie można określić deltę względem ceny
forward:
dla opcji
sprzedaży. Jednocześnie można określić deltę względem ceny
forward:
gdzie ![]() jest ceną forward w chwili
jest ceną forward w chwili
![]() instrumentu podstawowego dla kontraktu zapadalnego w
instrumentu podstawowego dla kontraktu zapadalnego w ![]() , a
, a ![]() jest formułą Blacka, to znaczy formułą Blacka-Scholesa w której cenę
bieżącą
jest formułą Blacka, to znaczy formułą Blacka-Scholesa w której cenę
bieżącą ![]() instrumentu podstawowego wyrażono przez cenę forward
instrumentu podstawowego wyrażono przez cenę forward
![]() , odpowiednio dla opcji kupna i opcji sprzedaży. Można pokazać
(Zadanie 10.1), że
, odpowiednio dla opcji kupna i opcji sprzedaży. Można pokazać
(Zadanie 10.1), że
Gamma
Korzystając z formuł (9.32) – (9.33) na wartość opcji kupna / sprzedaży otrzymujemy następujące wyrażenie na gammę opcji kupna / sprzedaży:
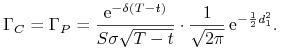 |
(10.6) |
Równość gammy opcji kupna i gammy opcji sprzedaży wynika z parytetu opcji kupna – sprzedaży. Oczywiście, są to gammy kupionych opcji (długich pozycji w tych opcjach).
Własności gammy
-
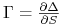 – Gamma mierzy wrażliwość delt na
zmianę ceny instrumentu podstawowego oraz określa w jakim stopniu
nieliniowość opcji jest istotna przy szacowaniu zmiany wartości
opcji.
– Gamma mierzy wrażliwość delt na
zmianę ceny instrumentu podstawowego oraz określa w jakim stopniu
nieliniowość opcji jest istotna przy szacowaniu zmiany wartości
opcji.
-
Jak widać ze wzoru (10.6), gamma (długiej pozycji) jest dodatnia. Stąd delty są funkcjami ściśle rosnącymi względem
 .
. -
Przy
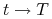
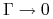 dla opcji OTM / ITM oraz
dla opcji OTM / ITM oraz
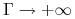 dla opcji ATM (
dla opcji ATM (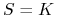 ). Stąd wynika iż
nieliniowość opcji jest najbardziej odczuwalna dla opcji ATM o
krótkim rezydualnym czasie trwania. Zabezpieczanie takich opcji jest
trudne (a raczej kłopotliwe i kosztowne), bowiem delta takich opcji
zmienia się stosunkowo szybko.
). Stąd wynika iż
nieliniowość opcji jest najbardziej odczuwalna dla opcji ATM o
krótkim rezydualnym czasie trwania. Zabezpieczanie takich opcji jest
trudne (a raczej kłopotliwe i kosztowne), bowiem delta takich opcji
zmienia się stosunkowo szybko. -
Gamma jest największa dla opcji dla których
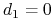 – czyli dla opcji które są niemal ATM.
– czyli dla opcji które są niemal ATM. -
Pozycja o dodatniej gammie wolniej traci na wartości / szybciej zyskuje na wartości przy zmianach ceny instrumentu podstawowego. Pozycja o ujemnej gammie (np. wystawione opcje) szybciej traci na wartości / wolniej zyskuje na wartości przy zmianach ceny instrumentu podstawowego – patrz wzór (10.2).
Vega
Korzystając z formuł (9.32) – (9.33) na wartość opcji kupna / sprzedaży otrzymujemy następujące wyrażenie na vegę opcji kupna / sprzedaży:
| (10.7) |
Równość vegi opcji kupna i vegi opcji sprzedaży wynika z parytetu opcji kupna-sprzedaży. Oczywiście, są to vegi kupionych opcji (długich pozycji w tych opcjach).
Własności Vegi
-
Jak widać ze wzoru (10.7), vega (długiej pozycji) jest dodatnia.
-
Vega mierzy wrażliwość wartości opcji na zmianę zmienności
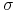 ceny instrumentu podstawowego.
ceny instrumentu podstawowego. -
Inaczej: vega mierzy błąd w wycenie opcji popełniany na skutek niepewności co do wartości zmienności
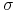 ceny
instrumentu podstawowego.
ceny
instrumentu podstawowego. -
Przy
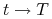
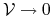 .
. -
Vega jest największa dla opcji dla których
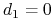 – czyli dla opcji które są
niemal ATM.
– czyli dla opcji które są
niemal ATM.
Rho / Rho![]()
Korzystając z formuł (9.32) – (9.33) na wartość opcji kupna / sprzedaży otrzymujemy następujące wyrażenia na
rho opcji kupna:
| (10.8) |
rho opcji sprzedaży:
| (10.9) |
gdzie, przypomnijmy,
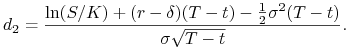 |
(10.10) |
Wzór na rho opcji sprzedaży (10.9) można również
wyprowadzić z wyrażenia (10.8) na rho opcji kupna i związku
między ![]() i
i ![]() , który wynika z parytetu opcji kupna –
sprzedaży. Oczywiście, są to rho kupionych opcji (długich pozycji w
tych opcjach).
, który wynika z parytetu opcji kupna –
sprzedaży. Oczywiście, są to rho kupionych opcji (długich pozycji w
tych opcjach).
Analogicznie wyznaczamy
rho![]() opcji kupna:
opcji kupna:
| (10.11) |
rho![]() opcji sprzedaży:
opcji sprzedaży:
| (10.12) |
Wzór na rho![]() opcji sprzedaży (10.12) można również
wyprowadzić z wyrażenia (10.11) na rho
opcji sprzedaży (10.12) można również
wyprowadzić z wyrażenia (10.11) na rho![]() opcji kupna i
związku między
opcji kupna i
związku między ![]() i
i ![]() , który wynika z parytetu
opcji kupna – sprzedaży. Oczywiście, są to rho
, który wynika z parytetu
opcji kupna – sprzedaży. Oczywiście, są to rho![]() kupionych opcji
(długich pozycji w tych opcjach).
kupionych opcji
(długich pozycji w tych opcjach).
Analizowanie współczynnika rho![]() ma szczególny sens w przypadku
opcji walutowych, kiedy w miejsce stopy dywidendy bierze się stopę
waluty bazowej (która jest czynnikiem ryzyka).
ma szczególny sens w przypadku
opcji walutowych, kiedy w miejsce stopy dywidendy bierze się stopę
waluty bazowej (która jest czynnikiem ryzyka).
Teta
Mimo iż czas nie jest czynnikiem ryzyka, analizując zmiany wartości opcji bada się jak cena tych opcji zmienia się z upływem czasu. Miarą tempa tej zmiany jest teta.
Korzystając z formuł (9.32) – (9.33) na wartość opcji kupna / sprzedaży otrzymujemy następujące wyrażenia na
tetę opcji kupna:
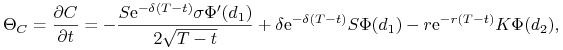 |
(10.13) |
tetę opcji sprzedaży:
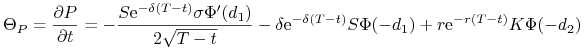 |
(10.14) |
Własności tety
-
Na ogół teta jest ujemna, bowiem zwykle wartość opcji maleje wraz z upływem czasu.
10.3. Równanie Blacka-Scholesa (związek między tetą, deltą i gammą)
Stosując aparat analizy stochastycznej można pokazać, że funkcja wyceniająca instrument pochodny spełnia następujące równanie różniczkowe cząstkowe:
| (10.15) |
Specyfikacja instrumentu pochodnego odbywa się przez postawienie warunków brzegowych które odpowiadają funkcji wypłaty instrumentu. Na przykład, w przypadku waniliowej opcji kupna tym warunkiem jest warunek końcowy, czyli warunek określający wypłatę w terminie zapadalności opcji, mianowicie
| (10.16) |
Można pokazać, że rozwiązaniem zagadnienia (10.15) –
(10.16) jest funkcja ![]() dana wzorem (9.32).
Oczywiście, aby zagadnienie (10.15) – (10.16)
było dobrze postawione należy jeszcze określić co rozumiemy przez
rozwiązanie, bowiem jak widać rozpatrując je w klasycznym sensie
będziemy mieli kłopot jako że funkcja występująca po prawej stronie
(10.16) nie jest różniczkowalna w
dana wzorem (9.32).
Oczywiście, aby zagadnienie (10.15) – (10.16)
było dobrze postawione należy jeszcze określić co rozumiemy przez
rozwiązanie, bowiem jak widać rozpatrując je w klasycznym sensie
będziemy mieli kłopot jako że funkcja występująca po prawej stronie
(10.16) nie jest różniczkowalna w ![]() .
.
Równanie Blacka-Scholesa (10.15) wiąże ze sobą współczynniki wrażliwości, mianowicie
| (10.17) |
i ten związek zarządzający portfelami instrumentów pochodnych powinni rozumieć i wykorzystywać analizując potencjalne zmiany wartości portfela. W szczególności, portfele są często tak konstruowane by były delta neutralne, czyli by ich delta wynosiła zero (w rzeczywistości by była bliska zera). Wówczas, dla takiego delta neutralnego portfela
| (10.18) |
Stąd, przy założeniu, że składnik ![]() po prawej stronie równania
(10.18) jest zaniedbywalnie mały w porównaniu z pozostałymi
wyrażeniami, wynika, że duża dodatnia gamma portfela implikuje iż
teta portfela będzie duża co do wartości bezwzględnej i ujemna. Tak
więc delta neutralny portfel o dużej dodatniej gammie będzie dużo
tracił na wartości z tytułu upływu czasu. Podstawowym przykładem
takiego portfela jest strategia opcyjna (long) straddle
złożona z dwóch kupionych opcji ATM: opcji kupna i opcji sprzedaży,
przy czym tu przez opcję call (put) ATM rozumie się opcję, której
tzw. forward delta
po prawej stronie równania
(10.18) jest zaniedbywalnie mały w porównaniu z pozostałymi
wyrażeniami, wynika, że duża dodatnia gamma portfela implikuje iż
teta portfela będzie duża co do wartości bezwzględnej i ujemna. Tak
więc delta neutralny portfel o dużej dodatniej gammie będzie dużo
tracił na wartości z tytułu upływu czasu. Podstawowym przykładem
takiego portfela jest strategia opcyjna (long) straddle
złożona z dwóch kupionych opcji ATM: opcji kupna i opcji sprzedaży,
przy czym tu przez opcję call (put) ATM rozumie się opcję, której
tzw. forward delta ![]() (
(![]() , odpowiednio) wynosi
, odpowiednio) wynosi ![]() (-
(-![]() , odpowiednio), czyli opcje o takiej cenie wykonania
by
, odpowiednio), czyli opcje o takiej cenie wykonania
by ![]() .
.
10.4. Współczynniki wrażliwości portfela instrumentów pochodnych
Rozpatrzmy portfel złożony z ![]() instrumentów pochodnych o takim
samym instrumencie podstawowym. Niech
instrumentów pochodnych o takim
samym instrumencie podstawowym. Niech
![]() oznacza funkcję, która wycenia
oznacza funkcję, która wycenia
![]() ty instrument w portfelu. Mimo iż instrument podstawowy jest ten
sam w każdym z tych instrumentów, stopy procentowe
ty instrument w portfelu. Mimo iż instrument podstawowy jest ten
sam w każdym z tych instrumentów, stopy procentowe ![]() i
i
![]() oraz zmienność
oraz zmienność ![]() mogą być specyficznymi
zmiennymi dobranymi odpowiednio do parametrów instrumentu pochodnego
– na przykład dla opcji waniliowych tenor stóp procentowych będzie
odpowiadał czasowi trwania instrumentu pochodnego, a zmienność
(implikowana) czasowi trwania i cenie wykonania. Niech
mogą być specyficznymi
zmiennymi dobranymi odpowiednio do parametrów instrumentu pochodnego
– na przykład dla opcji waniliowych tenor stóp procentowych będzie
odpowiadał czasowi trwania instrumentu pochodnego, a zmienność
(implikowana) czasowi trwania i cenie wykonania. Niech
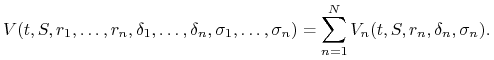 |
Wówczas
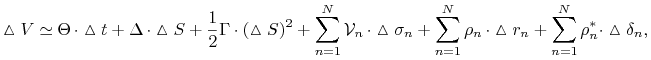 |
gdzie
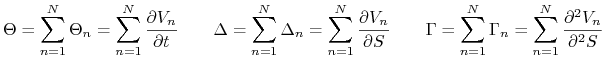 |
oraz
W przypadku
gdy ![]() ,
, ![]() oraz
oraz ![]() , mamy wzór analogiczny do (10.3):
, mamy wzór analogiczny do (10.3):
gdzie
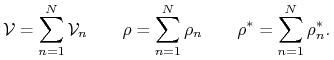 |
10.5. Obliczanie współczynników wrażliwości metodą ilorazu różnicowego
Dla instrumentów pochodnych które, wycenia się za pomocą złożonych algorytmów numerycznych (na przykład: stosując model dwumianowy, metodę symulacji Monte-Carlo, czy też rozwiązując numerycznie równanie Blacka-Scholesa), współczynniki wrażliwości można obliczać w sposób przybliżony za pomocą odpowiednich ilorazów różnicowych (o ile te algorytmy wyceny nie dostarczają jednocześnie wartości tych współczynników). I tak, na przykład
| (10.19) |
dla dostatecznie małego przyrostu ![]() . Iloraz różnicowy
po prawej stronie (10.19) przybliża deltę z dokładnością do
wyrazów rzędu
. Iloraz różnicowy
po prawej stronie (10.19) przybliża deltę z dokładnością do
wyrazów rzędu ![]() . W uzupełnieniu do delty
policzonej wzorem (10.19) rozważa się również delty
kierunkowe (jednostronne), które odpowiadają wzrostowi / spadkowi
ceny instrumentu podstawowego
. W uzupełnieniu do delty
policzonej wzorem (10.19) rozważa się również delty
kierunkowe (jednostronne), które odpowiadają wzrostowi / spadkowi
ceny instrumentu podstawowego
| (10.20) | |||
gdzie ![]() . Te delty mają zastosowanie w sytuacjach
gdy oczekuje się zmiany ceny instrumentu podstawowego w określonym
kierunku. Ponieważ
. Te delty mają zastosowanie w sytuacjach
gdy oczekuje się zmiany ceny instrumentu podstawowego w określonym
kierunku. Ponieważ
| (10.21) |
w tych deltach odzwierciedlony jest efekt nieliniowości (wypukłości) opcji.
Analogicznie można obliczać pozostałe współczynniki pierwszego rzędu – vegę i tetę.
Jak widać z (10.21), gammę można obliczyć następującym wyrażeniem:
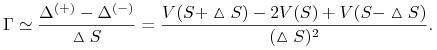 |
(10.22) |
10.6. Zabezpieczanie portfela instrumentów pochodnych
Portfel instrumentów pochodnych jest
-
delta neutralny jeżeli jego delta jest równa zero,
-
gamma neutralny jeżeli jego gamma jest równa zero,
-
delta-gamma neutralny jeżeli jego delta i gamma są równe zero,
-
vega neutralny jeżeli jego vega jest równa zero,
-
delta-gamma-vega neutralny jeżeli jego delta, gamma oraz vega są równe zero.
Poniżej opiszemy metody budowania portfeli neutralnych względem odpowiednich czynników ryzyka. Ogólnie mówiąc, metody te będą polegały na dołączeniu w odpowiedniej ilości do zabezpieczanego portfela wybranych instrumentów pochodnych, których instrument podstawowy jest identyczny z instrumentem podstawowym portfela.
Tworzenie portfela delta neutralnym
Rozpatrzmy portfel instrumentów pochodnych zależnych od tego samego instrumentu podstawowego, który nie jest delta neutralny, to jest
gdzie
![]() jest funkcją wyceniającą ten portfel.
Rozpatrzmy pewien instrument pochodny wyceniany funkcją
jest funkcją wyceniającą ten portfel.
Rozpatrzmy pewien instrument pochodny wyceniany funkcją
![]() , którego delta
, którego delta ![]() . Ten
instrument będzie pełnił rolę instrumentu zabezpieczającego. Po
dołączeniu do zabezpieczanego portfela
. Ten
instrument będzie pełnił rolę instrumentu zabezpieczającego. Po
dołączeniu do zabezpieczanego portfela ![]() jednostek instrumentu
zabezpieczającego wartość powiększonego portfela wyniesie
jednostek instrumentu
zabezpieczającego wartość powiększonego portfela wyniesie
Ten powiększony portfel będzie delta neutralny (będzie uodporniony na małe zmiany ceny instrumentu podstawowego), to jest
jeśli ilość instrumentu zabezpieczającego będzie wynosić
Rozpatrzmy szczególny
przypadek kiedy zabezpieczany portfel składa się tylko z jednej
wystawionej waniliowej opcji kupna, a instrumentem zabezpieczającym
jest instrument podstawowy opcji. W naszej notacji ![]() oraz
oraz
![]() . Zatem, kupno
. Zatem, kupno
jednostek instrumentu podstawowego razem z wystawioną opcją kupna tworzy portfel delta neutralny.
Tworzenie portfela gamma neutralnym
Postępujemy analogicznie jak w przypadku tworzenia portfela delta
neutralnym. Jeżeli portfel ma niezerową gammę (![]() ),
to po dołączeniu do niego
),
to po dołączeniu do niego
jednostek instrumentu zabezpieczającego o niezerowej gammie
![]() , otrzymamy portfel gamma neutralny.
, otrzymamy portfel gamma neutralny.
Tworzenie portfela delta-gamma neutralnym
Portfel delta-gamma neutralny możemy zbudować w dwóch krokach – najpierw robimy portfel gamma neutralnym, a następnie dobierając odpowiednią ilość jednostek instrumentu podstawowego zerujemy deltę zabezpieczanego portfela.
W ogólnym przypadku do zabezpieczanego portfela dokładamy dwa
instrumenty zabezpieczające o funkcjach wyceny ![]() i
i ![]() w
ilościach
w
ilościach ![]() i
i ![]() jednostek, odpowiednio. Wówczas wartość tak
powiększonego portfela wynosi
jednostek, odpowiednio. Wówczas wartość tak
powiększonego portfela wynosi
Ten portfel będzie delta-gamma neutralny, jeśli
| (10.23) |
Układ równań (10.23) ma jednoznaczne rozwiązanie, jeżeli wyznacznik tego układu jest różny od zera, to jest gdy
| (10.24) |
Wybierając instrumenty zabezpieczające musimy uważać by warunek (10.24) był spełniony. Jeżeli jednym z instrumentów zabezpieczających jest instrument podstawowy, to dla spełnienia warunku (10.24) wystarczy by gamma drugiego instrumentu zabezpieczającego była niezerowa i wówczas portfel zabezpieczony będzie identyczny z tym który uzyskalibyśmy stosując metodę zabezpieczania opisaną na początku tego ustępu.
Tworzenie portfela vega neutralnym
Postępujemy analogicznie jak w przypadku tworzenia portfela delta
neutralnym. Jeżeli portfel ma niezerową vegę
(![]() ), to po dołączeniu do niego
), to po dołączeniu do niego
jednostek instrumentu
zabezpieczającego o niezerowej vedze ![]() , otrzymamy
portfel vega neutralny.
, otrzymamy
portfel vega neutralny.
Tworzenie portfela delta-gamma-vega neutralnym
Tym razem do zabezpieczanego portfela musimy dołożyć trzy
instrumenty zabezpieczające o funkcjach wyceny ![]() ,
, ![]() i
i ![]() w ilościach
w ilościach ![]() ,
, ![]() i
i ![]() jednostek, odpowiednio. Wówczas wartość
tak powiększonego portfela wynosi
jednostek, odpowiednio. Wówczas wartość
tak powiększonego portfela wynosi
Ten portfel będzie delta-gamma-vega neutralny, jeśli
| (10.25) |
Układ równań (10.25) ma jednoznaczne rozwiązanie, jeżeli
wyznacznik tego układu jest różny od zera. Jeżeli jako pierwszy z
instrumentów zabezpieczających wybierzemy instrument podstawowy,
czyli gdy ![]() , to układ (10.25) upraszcza się w
następujący sposób:
, to układ (10.25) upraszcza się w
następujący sposób:
| (10.26) |
10.7. Dynamiczne zabezpieczanie portfela instrumentów pochodnych
Dynamiczne zabezpieczanie portfela instrumentów pochodnych polega na relatywnie częstym modyfikowaniu składu portfela tak by mimo zmieniającej się sytuacji rynkowej profil ryzyka portfela, widziany przez pryzmat jego wybranych współczynników wrażliwości, nie zmieniał się. Polega to na kupowaniu lub sprzedawaniu odpowiedniej ilości instrumentu podstawowego i/lub instrumentów pochodnych na ten instrument zgodnie z regułami wcześniej przedstawionymi.
Dynamiczny delta hedging portfela
Rozpatrzmy sytuację kiedy dealer, który wystawił instrument
pochodny, zamierza całkowicie zabezpieczyć swoją pozycję tworząc
portfel replikujący złożony z odpowiedniej pozycji w instrumencie
podstawowym i pozycji w instrumencie wolnym od ryzyka (to jest w
gotówce na rachunku bankowym oprocentowanym po stopie wolnej od
ryzyka), a następnie dynamicznie modyfikować ten portfel w
zależności od wartości instrumentu podstawowego. Przypuśćmy, że za
wystawienie instrumentu pochodnego dealer otrzymał kwotę ![]() ,
delta tego instrumentu (długiej pozycji w tym instrumencie) wynosiła
,
delta tego instrumentu (długiej pozycji w tym instrumencie) wynosiła
![]() , a w momencie wystawienia tego instrumentu wartość jego
instrumentu podstawowego wynosiła
, a w momencie wystawienia tego instrumentu wartość jego
instrumentu podstawowego wynosiła ![]() . Portfel replikujący
stworzony w chwili wystawienia instrumentu pochodnego jest złożony z
. Portfel replikujący
stworzony w chwili wystawienia instrumentu pochodnego jest złożony z
-
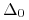 sztuk instrumentu podstawowego,
sztuk instrumentu podstawowego, -
kwoty
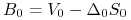 na rachunku bankowym.
na rachunku bankowym.
Załóżmy, że dealer dokonuje modyfikacji tego portfela w chwili
![]() , kiedy wartość instrumentu podstawowego wynosi
, kiedy wartość instrumentu podstawowego wynosi ![]() , a delta
instrumentu pochodnego wynosi
, a delta
instrumentu pochodnego wynosi ![]() . W tym momencie portfel
replikujący jest złożony z
. W tym momencie portfel
replikujący jest złożony z
-
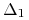 sztuk instrumentu podstawowego,
sztuk instrumentu podstawowego, -
kwoty
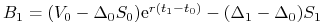 na rachunku bankowym,
na rachunku bankowym,
bowiem dealer musiał zmodyfikować pozycje w instrumencie podstawowym
o ![]() sztuk instrumentu podstawowego, finansując to
kwotą
sztuk instrumentu podstawowego, finansując to
kwotą ![]() z rachunku bankowego.
z rachunku bankowego.
Analogicznie, portfel replikujący w chwili ![]() , kiedy wartość
instrumentu podstawowego wynosi
, kiedy wartość
instrumentu podstawowego wynosi ![]() , a delta instrumentu
pochodnego wynosi
, a delta instrumentu
pochodnego wynosi ![]() , złożony jest z
, złożony jest z
-
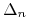 sztuk instrumentu podstawowego,
sztuk instrumentu podstawowego, -
kwoty
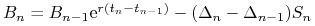 na rachunku bankowym.
na rachunku bankowym.
Powyższa strategia powinna w chwili wygaśnięcia instrumentu pochodnego dać pozycję, która dostatecznie dobrze zreplikuje wypłatę z tego instrumentu – to jak dobrze zależy od częstotliwości z jaką portfel replikujący był modyfikowany. W krańcowym przypadku, kiedy modyfikacje portfela odbywałyby się w sposób ciągły, powinniśmy otrzymać dokładnie wypłatę z tego instrumentu pochodnego.
W praktyce delta hedging odbywa się co jakiś czas (jak jest on długi zależy od sytuacji na rynku – od kilku godzin do tygodnia) i związany jest kosztami transakcyjnymi kupna/sprzedaży instrumentu podstawowego, które wpływają na opłacalność tej strategii zabezpieczającej. Na ogół nie opłaca się prowadzić delta hedgingu dla pojedynczych instrumentów pochodnych, bo w tym przypadku koszty transakcyjne są zwykle znaczne w stosunku do wartości zabezpieczanego instrumentu. Natomiast, delta hedging portfela instrumentów pochodnych (na ten sam instrument podstawowy) o odpowiednio dużej wartości może być opłacalny.
Zagadnienia i zadania na Ćwiczenia
Ćwiczenie 10.1
Oblicz delty względem ceny forward dla opcji waniliowych wycenianych w modelu Blacka-Scholesa.
Ćwiczenie 10.2
Oblicz współczynniki wrażliwości dla opcji binarnych wycenianych w modelu Blacka-Scholesa.
Ćwiczenie 10.3
Rozpatrzmy europejską opcję kupna o czasie trwania ![]() (3
miesiące). Cena aktywa wynosi
(3
miesiące). Cena aktywa wynosi ![]() PLN, stopa procentowa
PLN, stopa procentowa ![]() ,
stopa dywidendy
,
stopa dywidendy ![]() , oraz zmienność
, oraz zmienność ![]() . Niech
cena wykonania wynosi
. Niech
cena wykonania wynosi ![]() PLN. Oblicz
PLN. Oblicz
-
cenę opcji,
-
wartości współczynników wrażliwości tej opcji,
-
przybliżone wartości dziennej zmiany
 ,
, 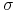 ,
, 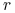 ,
, 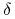 odpowiadające 1.65 odchylenia standardowego tych wielkości – załóż,
że zmienność stóp wynosi
odpowiadające 1.65 odchylenia standardowego tych wielkości – załóż,
że zmienność stóp wynosi 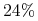 , a zmienność zmienności wynosi
, a zmienność zmienności wynosi
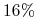 ,
, -
wartości zmiany ceny opcji odpowiadające wyznaczonym powyżej zmianom
 ,
, 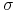 ,
, 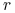 ,
, 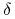 .
.
Ćwiczenie 10.4
Rozpatrzmy portfel złożony z następujących opcji na kurs USD/PLN:
-
kupiony 3M call USD/put PLN o wartości nominalnej
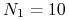 mln USD z ceną
wykonania
mln USD z ceną
wykonania 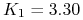 USD/PLN,
USD/PLN, -
sprzedany 1M call USD/put PLN o wartości nominalnej
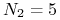 mln USD z ceną
wykonania
mln USD z ceną
wykonania 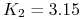 USD/PLN,
USD/PLN, -
sprzedany 6M put USD/call PLN o wartości nominalnej
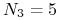 mln USD z ceną
wykonania
mln USD z ceną
wykonania 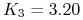 USD/PLN
USD/PLN
oraz transakcji 3M FX forward na sprzedaż ![]() mln USD po
kursie
mln USD po
kursie ![]() USD/PLN.
USD/PLN.
Przy założeniu, że bieżący kurs wynosi ![]() USD/PLN, oraz dla
USD/PLN, oraz dla
-
1M:
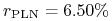 ,
, 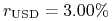 ,
, 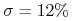 ,
, -
3M:
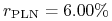 ,
, 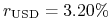 ,
, 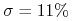 ,
, -
6M:
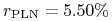 ,
, 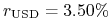 ,
,  ,
,
oblicz deltę tego portfela. Jaką transakcję FX spot należy zawrzeć by portfel był delta neutralny?
Ćwiczenie 10.5
Rozpatrzmy delta neutralny portfel, którego gamma wynosi - 2000 a vega -4000. Na rynku w płynnym obrocie znajdują się opcje:
-
jedna o delcie 0.6, gammie 0.5, i vedze 2.0,
-
druga o delcie 0.4, gammie 0.8, i vedze 1.5.
Zabezpiecz ten portfel tak, by był on
-
(a) delta-vega neutralny,
-
(b) delta-gamma-vega neutralny.
Oczywiście zakładamy, że portfel oraz opcje zależą od tego samego instrumentu podstawowego.
Ćwiczenie 10.6
Zakładając, że funkcja wyceniająca instrument pochodny spełnia
równanie Blacka-Scholesa (10.15), wyprowadź równanie na
vegę ![]() tego instrumentu pochodnego.
tego instrumentu pochodnego.
Ćwiczenie 10.7
Rozpatrzmy 3M opcję kupna na akcje spółki wuwu.com z ceną
wykonania ![]() PLN. Bieżąca cena akcji wynosi 100, a jej
zmienność 36.47%. Wolna od ryzyka stopa procentowa dla 3M
lokat/depozytów wynosi 6.67%. Zakładamy, że spółka nie płaci
dywidendy w czasie trwania opcji. Jaką pozycję w akcjach tej spółki
należy utworzyć by portfel złożony z tej pozycji oraz z 10-ciu
wystawionych opcji kupna był delta neutralny? Jaką sumę pieniędzy
należy pożyczyć by sfinansować ten portfel?
PLN. Bieżąca cena akcji wynosi 100, a jej
zmienność 36.47%. Wolna od ryzyka stopa procentowa dla 3M
lokat/depozytów wynosi 6.67%. Zakładamy, że spółka nie płaci
dywidendy w czasie trwania opcji. Jaką pozycję w akcjach tej spółki
należy utworzyć by portfel złożony z tej pozycji oraz z 10-ciu
wystawionych opcji kupna był delta neutralny? Jaką sumę pieniędzy
należy pożyczyć by sfinansować ten portfel?
Ćwiczenie 10.8
Udowodnij, że dowolny delta neutralny portfel złożony z
-
wystawionych opcji waniliowych (na ten sam instrument podstawowy),
-
odpowiedniej pozycji zabezpieczającej w instrumencie podstawowym,
-
pozycji gotówkowej finansującej ten portfel,
zyskuje na wartości z upływem czasu przy niezmienionych cenie i zmienności instrumentu podstawowego oraz przy niezmienionej stopie procentowej.
Ćwiczenie 10.9 (Nieefektywność strategii stop-loss dla opcji kupna)
Rozpatrzmy sytuację kiedy dealer, który wystawił opcję kupna akcji
po cenie ![]() i zamierza zabezpieczać swoją pozycję kupując akcję po
cenie
i zamierza zabezpieczać swoją pozycję kupując akcję po
cenie ![]() jak tylko cena akcji przekroczy wartość
jak tylko cena akcji przekroczy wartość ![]() i sprzedawać
akcję po cenie
i sprzedawać
akcję po cenie ![]() jak tylko cena akcji spadnie poniżej
jak tylko cena akcji spadnie poniżej ![]() .
Dlaczego ta strategia nie może działać?
.
Dlaczego ta strategia nie może działać?




