Zagadnienia
- 12.1 Proste instrumenty pochodne stopy procentowej
- 12.2 Caplet / Floorlet
- 12.3 Związek capletów / floorletów z opcjami na obligacje zerokuponowe
- 12.4 Cap / Floor
- 12.5 Binary cap / binary floor
- 12.6 Swapcje – opcje na kontrakty IRS
- 12.7 Niespójność modelu Blacka'76
- 12.8 Finansowe produkty strukturalne z wbudowanymi opcjami na stopę procentową
- 12.9 Zagadnienia i zadania na Ćwiczenia
12. Instrumenty pochodne stopy procentowej
12.1. Proste instrumenty pochodne stopy procentowej
Instrumenty pochodne, których wypłaty zależą od struktury stóp procentowych, są na ogół instrumentami o znacznej złożoności. Ich wycena wymaga dużo bardziej zaawansowanych metod i modeli niż model Blacka-Scholesa, a zabezpieczanie takich instrumentów jest bardzo skomplikowane. Instrumenty pochodne stopy procentowej, w pewnym sensie, są wyeksponowane na wiele wzajemnie oddziaływujących czynników ryzyka. Podstawą do rozumienia inżynierii takich instrumentów są proste pochodne stopy procentowej (pochodne pierwszej generacji), które zależą jedynie od poziomu pewnych stóp procentowych. Na tym wykładzie omówimy najważniejsze takie instrumenty pochodne, mianowicie:
-
opcje na górny / dolny poziom stopy procentowej – caplet / floorlet
-
cap (seria capletów) / floor (seria floorletów)
-
binarne opcje stopy procentowej
-
opcje na kontrakty IRS – swapcje (swaptions)
-
opcje na obligacje zerokuponowe
i pokażemy w jaki sposób te instrumenty są wbudowywane w złożone produkty finansowe, na przykład:
-
inverse floater note,
-
range accrual note.
Mimo potencjalnych trudności z wyceną tych instrumentów pochodnych, w praktyce rynkowej przyjęty został prosty model – tzw. model Blacka (analogiczny do modelu Blacka – Scholesa), w którym zakłada się że instrument podstawowy opcji (stopa procentowa, cena obligacji) ma w terminie wygaśnięcia opcji rozkład log-normalny. Jak już wiemy przy takim założeniu waniliowe opcje europejskie można w prosty sposób wycenić (o ile znamy parametry tych rozkładów; patrz Lemat 9.3) – otrzymujemy tzw. formuły Blacka'76.
12.2. Caplet / Floorlet
Caplet / Floorlet to pojedyncza opcja kupna / sprzedaży
stopy rynkowej ![]() (typu LIBOR), której okres depozytowy
zaczyna się w terminie wygaśnięcia opcji
(typu LIBOR), której okres depozytowy
zaczyna się w terminie wygaśnięcia opcji ![]() i kończy się w
i kończy się w ![]() .
Wypłata tych opcji wynosi
.
Wypłata tych opcji wynosi
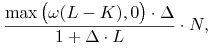 |
(12.1) |
gdzie
-
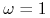 dla capleta i
dla capleta i 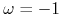 dla floorleta,
dla floorleta, -
 jest ceną wykonania (określającą poziom stopy procentowej),
jest ceną wykonania (określającą poziom stopy procentowej), -
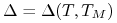 jest długością
okresu depozytowego stopy
jest długością
okresu depozytowego stopy 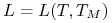 ,
, -
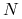 jest nominałem opcji wyrażonym w
walucie stopy
jest nominałem opcji wyrażonym w
walucie stopy 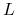 .
.
Struktura wypłaty (12.1) jest bardzo podobna do wypłaty kontraktu FRA do tego stopnia, że
| kupiony caplet |
(12.2) | |
Stąd wynika parytet dla capletów – floorletów, mianowicie
| (12.3) |
gdzie ![]() oraz
oraz ![]() oznaczają
bieżące ceny capleta oraz floorleta. Posiadacz capleta jest
zabezpieczony przed wzrostem stopy procentowej powyżej stopy będącej
ceną wykonania tej opcji. Dlatego capleta określa się jako opcję na
górny poziom stopy procentowej. Podobnie floorlet jest opcją na
dolny poziom stopy procentowej, która zabezpiecza posiadacza przed
spadkiem stopy procentowej poniżej stopy będącej ceną wykonania tej
opcji.
oznaczają
bieżące ceny capleta oraz floorleta. Posiadacz capleta jest
zabezpieczony przed wzrostem stopy procentowej powyżej stopy będącej
ceną wykonania tej opcji. Dlatego capleta określa się jako opcję na
górny poziom stopy procentowej. Podobnie floorlet jest opcją na
dolny poziom stopy procentowej, która zabezpiecza posiadacza przed
spadkiem stopy procentowej poniżej stopy będącej ceną wykonania tej
opcji.
Wycena capleta / floorleta
Przy założeniu, że stopa ![]() w chwili
w chwili ![]() ma rozkład
log-normalny taki, że
ma rozkład
log-normalny taki, że
-
odchylenie standardowe
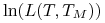 wynosi
wynosi 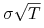 ,
, -
wartość oczekiwana stopy
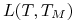 jest równa aktualnie obserwowanej stopie forward
jest równa aktualnie obserwowanej stopie forward
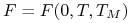 na okres czasu
na okres czasu ![[T,T_{M}]](wyklady/ifi/mi/mi1630.png) ,
,
bieżąca cena capleta (![]() ) / floorleta (
) / floorleta (![]() ) o cenie
wykonania
) o cenie
wykonania ![]() wynosi
wynosi
| (12.4) |
gdzie
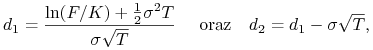 |
(12.5) |
a ![]() jest czynnikiem, który dyskontuje z chwili
jest czynnikiem, który dyskontuje z chwili ![]() na
chwilę bieżącą. Czynnik ten możemy oczywiście zapisać w postaci
na
chwilę bieżącą. Czynnik ten możemy oczywiście zapisać w postaci
![]() , gdzie
, gdzie ![]() jest stopą wolną od ryzyka.
jest stopą wolną od ryzyka.
12.3. Związek capletów / floorletów z opcjami na obligacje zerokuponowe
Rozpatrzmy opcję sprzedaży obligacji zerokuponowej, która wypłaca
jednostkowy nominał w chwili ![]() . Opcja wygasając w chwili
. Opcja wygasając w chwili ![]() ,
wypłaca
,
wypłaca
| (12.6) |
gdzie ![]() jest ceną wykonania,
jest ceną wykonania, ![]() obserwowaną w chwili
wygaśnięcia opcji ceną obligacji, a
obserwowaną w chwili
wygaśnięcia opcji ceną obligacji, a ![]() jest nominałem opcji.
Jeżeli cenę wykonania i cenę obligacji wyrazimy w terminach stóp
procentowych, mianowicie
jest nominałem opcji.
Jeżeli cenę wykonania i cenę obligacji wyrazimy w terminach stóp
procentowych, mianowicie
gdzie
![]() oraz
oraz ![]() , to po przekształceniu
wyrażenia na wypłatę (12.6) otrzymamy następującą formułę
, to po przekształceniu
wyrażenia na wypłatę (12.6) otrzymamy następującą formułę
która będzie identyczna z (12.1) w przypadku
![]() , czyli capleta, o ile
, czyli capleta, o ile ![]() . Analogiczny rezultat
otrzymamy dla opcji kupna obligacji zerokuponowej i floorleta.
. Analogiczny rezultat
otrzymamy dla opcji kupna obligacji zerokuponowej i floorleta.
12.4. Cap / Floor
Cap / Floor to seria capletów / floorletów na stopy
procentowe dla kolejnych jednakowych okresów depozytowych łącznie
obejmujących czas trwania capa / floora, wszystkie z tą samą ceną
wykonania ![]() i jednakowym nominałem
i jednakowym nominałem ![]() . Standardowo capy / floory
są kwotowane dla okresów czasu będących pełnymi krotnościami roku,
przy czym stopą tych kontraktów jest 3M lub 6M stopa typu LIBOR.
. Standardowo capy / floory
są kwotowane dla okresów czasu będących pełnymi krotnościami roku,
przy czym stopą tych kontraktów jest 3M lub 6M stopa typu LIBOR.
Rozpatrzmy ![]() -letni cap / floor na 3M stopę LIBOR. Ponieważ dla
pierwszego 3M okresu stopa LIBOR jest ustalona przez rynek,
-letni cap / floor na 3M stopę LIBOR. Ponieważ dla
pierwszego 3M okresu stopa LIBOR jest ustalona przez rynek,
![]() -letni cap / floor składa się z
-letni cap / floor składa się z ![]() trzymiesięcznych capletów
/ floorletów. Podobnie,
trzymiesięcznych capletów
/ floorletów. Podobnie, ![]() -letni cap / floor na 6M stopę LIBOR
składa się z
-letni cap / floor na 6M stopę LIBOR
składa się z ![]() sześciomiesięcznych capletów / floorletów. Cena
capa / floora jest sumą cen poszczególnych (żyjących) capletów /
floorletów. I tak, jeśli wycena odbywa się przed terminem
zapadalności pierwszego capleta / floorleta, to
sześciomiesięcznych capletów / floorletów. Cena
capa / floora jest sumą cen poszczególnych (żyjących) capletów /
floorletów. I tak, jeśli wycena odbywa się przed terminem
zapadalności pierwszego capleta / floorleta, to
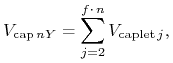 |
(12.7) |
gdzie ![]() oznacza liczbę capletów / floorletów przypadającą na okres
jednego roku.
oznacza liczbę capletów / floorletów przypadającą na okres
jednego roku.
Rynek kwotuje ceny capów / floorów podając wartość zmienności
implikowanej ![]() , gdzie
, gdzie ![]() oznacza długość
kontraktu (w latach, to jest,
oznacza długość
kontraktu (w latach, to jest, ![]() ) a
) a ![]() jest ceną wykonania.
Jest to tak zwana płaska zmienność implikowana (ang. flat
implied volatility). Ta wartość jest używana do obliczenia ceny
capa / floora za pomocą wzoru (12.7), przy czym każdy
caplet / floorlet wchodzący w skład jednego capa / floora jest
wyceniany formułą (12.4) z tą samą wartością zmienności
jest ceną wykonania.
Jest to tak zwana płaska zmienność implikowana (ang. flat
implied volatility). Ta wartość jest używana do obliczenia ceny
capa / floora za pomocą wzoru (12.7), przy czym każdy
caplet / floorlet wchodzący w skład jednego capa / floora jest
wyceniany formułą (12.4) z tą samą wartością zmienności
![]() . Ceny gotówkowe capów i floorów są zwykle
podawane jako procent nominału wyrażony w punktach bazowych (bp).
. Ceny gotówkowe capów i floorów są zwykle
podawane jako procent nominału wyrażony w punktach bazowych (bp).
Mając do dyspozycji ceny (płaskie zmienności implikowane) dla serii
capów / floorów o czasach trwania różniących się tenorem stopy (na
przykład, każdy kolejny cap jest dłuższy od poprzedniego o 3M),
można wyliczyć wartości zmienności implikowanej dla poszczególnych
capletów / floorletów. Wartość zmienności implikowanej ![]()
![]() -tego capleta / floorleta dla ceny wykonania
-tego capleta / floorleta dla ceny wykonania ![]() wyznaczamy z
warunku
wyznaczamy z
warunku
| (12.8) |
gdzie ![]() oznacza czas trwania capleta / floorleta. W
rzeczywistości, rynek kwotuje capy / floory dla czasów trwania,
które są pełnymi krotnościami roku i wówczas aby móc wyznaczyć
zmienności implikowane
oznacza czas trwania capleta / floorleta. W
rzeczywistości, rynek kwotuje capy / floory dla czasów trwania,
które są pełnymi krotnościami roku i wówczas aby móc wyznaczyć
zmienności implikowane ![]() korzystając z wzoru
(12.8) trzeba przyjąć dodatkowe założenia, na przykład
zinterpolować brakujące ceny capów / floorów zapadających pomiędzy
pełnymi kolejnymi latami.
korzystając z wzoru
(12.8) trzeba przyjąć dodatkowe założenia, na przykład
zinterpolować brakujące ceny capów / floorów zapadających pomiędzy
pełnymi kolejnymi latami.
Ponieważ dla capletów i floorletów zachodzi związek (12.2), to dla capów i floorów mamy analogicznie
| (12.9) |
gdzie kontrakt forward IRS zaczyna się w tej samej chwili czasu w której zapada pierwszy caplet / floorlet i kończy się w chwili w której teoretycznie byłaby płacona stopa LIBOR ostatniego capleta / floorleta. Ze związku (12.9) wynika natychmiast następujący parytet cap – floor
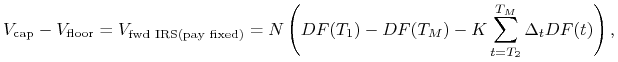 |
(12.10) |
gdzie ![]() i
i ![]() są odpowiednio początkiem i końcem pierwszego
capleta / floorleta,
są odpowiednio początkiem i końcem pierwszego
capleta / floorleta, ![]() jest końcem ostatniego capleta /
floorleta, a
jest końcem ostatniego capleta /
floorleta, a ![]() oznacza długość okresu capleta / floorleta
który wygasa w chwili
oznacza długość okresu capleta / floorleta
który wygasa w chwili ![]() .
.
Collar jest strategią złożoną z kupionego capa z ceną
wykonania ![]() i sprzedanego floora z ceną wykonania
i sprzedanego floora z ceną wykonania
![]() , przy czym oba kontrakty opiewają
na ten sam nominał. Kupując taką strategię inwestor zapewnia sobie
finansowanie po stopie
, przy czym oba kontrakty opiewają
na ten sam nominał. Kupując taką strategię inwestor zapewnia sobie
finansowanie po stopie ![]() nie większej niż
nie większej niż ![]() ale
jednocześnie by obniżyć koszt tego zabezpieczenia (to jest, koszt
strategii collar) akceptuje, że poziom stopy po której się będzie
finansował będzie wynosić co najmniej
ale
jednocześnie by obniżyć koszt tego zabezpieczenia (to jest, koszt
strategii collar) akceptuje, że poziom stopy po której się będzie
finansował będzie wynosić co najmniej ![]() . Taki
klient zwykle określa maksymalny poziom kosztu finansowania wyrażony
stopą
. Taki
klient zwykle określa maksymalny poziom kosztu finansowania wyrażony
stopą ![]() oraz koszt zabezpieczenia
oraz koszt zabezpieczenia ![]() i do tych wartości dobiera się cenę wykonania floora
i do tych wartości dobiera się cenę wykonania floora
![]() tak by
tak by
Typowy collar jest tak konstruowany by w chwili jego zawarcia jego wartość wynosiła zero.
12.5. Binary cap / binary floor
Binarny caplet / floorlet wypłaca kwotę w chwili
wygaśnięcia opcji ![]()
| (12.11) |
gdzie
-
 jeżeli
jeżeli  oraz
oraz 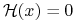 jeżeli
jeżeli 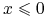 ,
, -
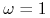 dla capleta i
dla capleta i 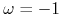 dla floorleta,
dla floorleta, -
 jest ceną wykonania (określającą poziom stopy procentowej),
jest ceną wykonania (określającą poziom stopy procentowej), -
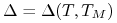 jest długością
okresu depozytowego stopy
jest długością
okresu depozytowego stopy 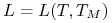 ,
, -
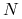 jest nominałem opcji wyrażonym w
walucie stopy
jest nominałem opcji wyrażonym w
walucie stopy 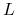 .
.
W modelu Blacka wycena binarnych capletów (![]() ) / floorletów
(
) / floorletów
(![]() ) dana jest wzorem
) dana jest wzorem
| (12.12) |
gdzie
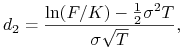 |
(12.13) |
a ![]() jest czynnikiem, który dyskontuje z chwili
jest czynnikiem, który dyskontuje z chwili ![]() na chwilę
bieżącą.
na chwilę
bieżącą.
Binarny cap / floor jest serią pojedynczych capletów / floorletów i oczywiście cena tych kontraktów jest sumą poszczególnych opcji z których się one składają. Binarne capy / floory są najczęściej elementami składowymi finansowych produktów strukturalnych.
12.6. Swapcje – opcje na kontrakty IRS
Swapcja (ang. swaption) jest opcją na kontrakt IRS, który rozpocznie się w terminie wygaśnięcia opcji.
Swapcja charakteryzuje się dwoma parametrami czasowymi – pierwszy z
nich oznacza termin wygaśnięcia (czas trwania) swapcji, a drugi to
długość (tenor) kontraktu IRS będącego instrumentem podstawowym
swapcji. W terminie wygaśnięcia, o ile będzie to korzystne dla
posiadacza swapcji, wejdzie on w kontrakt IRS ze stopą określoną
ceną wykonania opcji ![]() . Drugą stroną kontraktu IRS będzie wystawca
opcji. Są dwa rodzaje swapcji:
. Drugą stroną kontraktu IRS będzie wystawca
opcji. Są dwa rodzaje swapcji:
-
receiver's swaptions – opcje na kontrakt IRS w którym (od strony posiadacza opcji) będziemy otrzymywać stałą stopę kontraktu IRS (stopę
 ) i płacić stopę zmienną typu LIBOR;
) i płacić stopę zmienną typu LIBOR; -
payer's swaptions – opcje na kontrakt IRS w którym (od strony posiadacza opcji) będziemy płacić stałą stopę kontraktu IRS (stopę
 ) i
otrzymywać stopę zmienną typu LIBOR.
) i
otrzymywać stopę zmienną typu LIBOR.
Jak wynika z określenia tych swapcji w chwili wygaśnięcia zachodzi następujący związek
long payer's swaption ![]() short receiver's swaption
short receiver's swaption ![]() pay fixed
fwd IRS,
pay fixed
fwd IRS,
skąd otrzymujemy parytet dla swapcji w postaci
| (12.14) |
gdzie ![]() jest wartością w chwili wyceny
kontraktu forward IRS, który płaci stałą stopą
jest wartością w chwili wyceny
kontraktu forward IRS, który płaci stałą stopą ![]() i zaczyna się w
chwili wygaśnięcia opcji.
i zaczyna się w
chwili wygaśnięcia opcji.
Związek swapcji z opcjami na obligacje kuponowe
W chwili wygaśnięcia ![]() wartość swapcji na jednostkę nominału
kontraktu IRS wynosi
wartość swapcji na jednostkę nominału
kontraktu IRS wynosi
gdzie
![]() jest wartością w chwili
jest wartością w chwili ![]() kontraktu IRS ze
stopą
kontraktu IRS ze
stopą ![]() . Kontrakt IRS ze stopą
. Kontrakt IRS ze stopą ![]() , w którym płacimy stopę stałą
, w którym płacimy stopę stałą
![]() , można (w sensie wyceny) uznać za kontrakt wymiany obligacji o
stałym kuponie oprocentowanym
, można (w sensie wyceny) uznać za kontrakt wymiany obligacji o
stałym kuponie oprocentowanym ![]() na obligację o zmiennym
oprocentowaniu. Wartość obligacji o zmiennym kuponie na początku
(każdego) okresu odsetkowego jest równa wartości nominalnej tej
obligacji. W związku z tym, receiver's / payer's swapcja jest
równoważna opcji kupna (call) / sprzedaży (put) obligacji o stałym
kuponie
na obligację o zmiennym
oprocentowaniu. Wartość obligacji o zmiennym kuponie na początku
(każdego) okresu odsetkowego jest równa wartości nominalnej tej
obligacji. W związku z tym, receiver's / payer's swapcja jest
równoważna opcji kupna (call) / sprzedaży (put) obligacji o stałym
kuponie ![]() , której cena wykonania jest równa wartości nominalnej
obligacji (swapcji).
, której cena wykonania jest równa wartości nominalnej
obligacji (swapcji).
Wycena swapcji
Rozpatrzmy payer's swaption o wartości nominalnej 1. Wówczas,
wartość, w chwili ![]() , kontraktu IRS będącego instrumentem
podstawowym opcji wynosi
, kontraktu IRS będącego instrumentem
podstawowym opcji wynosi
| (12.15) |
gdzie ![]() jest ceną obligacji, której kupon wynosi
jest ceną obligacji, której kupon wynosi ![]() . Z drugiej
strony, kontrakty IRS zawierane w chwili
. Z drugiej
strony, kontrakty IRS zawierane w chwili ![]() mają stopę
mają stopę ![]() taką,
że obligacja o kuponie
taką,
że obligacja o kuponie ![]() jest at par, to znaczy
jest at par, to znaczy ![]() .
Zatem
.
Zatem
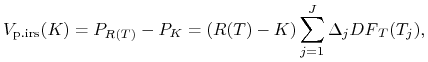 |
(12.16) |
gdzie ![]() jest długością
jest długością ![]() -tego okresu odsetkowego nogi
stałej kontraktu IRS, a
-tego okresu odsetkowego nogi
stałej kontraktu IRS, a ![]() czynnikiem, który dyskontuje z
końca tego okresu
czynnikiem, który dyskontuje z
końca tego okresu ![]() do chwili początkowej kontraktu IRS (według
struktury stóp obowiązującej w chwili
do chwili początkowej kontraktu IRS (według
struktury stóp obowiązującej w chwili ![]() ). Z (12.16)
wynika, że payer's swapcja będzie wykonywana jeżeli stopa kontraktów
IRS w chwili wygaśnięcia opcji jest większa niż cena wykonania
swapcji. Ponadto, wzór (12.16) pozwala nam uważać payer's
swapcję za zestaw
). Z (12.16)
wynika, że payer's swapcja będzie wykonywana jeżeli stopa kontraktów
IRS w chwili wygaśnięcia opcji jest większa niż cena wykonania
swapcji. Ponadto, wzór (12.16) pozwala nam uważać payer's
swapcję za zestaw ![]() opcji kupna na stopę
opcji kupna na stopę ![]() zapadalnych w
chwili
zapadalnych w
chwili ![]() o tej samej cenie wykonania
o tej samej cenie wykonania ![]() , wpłata których jest
proporcjonalna do długości kolejnych okresów odsetkowych nogi stałej
kontraktu IRS – dokładniej, wartość wypłaty
, wpłata których jest
proporcjonalna do długości kolejnych okresów odsetkowych nogi stałej
kontraktu IRS – dokładniej, wartość wypłaty ![]() -tej takiej opcji w
-tej takiej opcji w
![]() wynosi
wynosi
| (12.17) |
Struktura wypłaty (12.17) jest niemal analogiczna jak
wypłata capleta dana wzorem (12.1) dla ![]() .
.
Zatem, jeżeli założymy, że stopa ![]() kontraktu IRS w chwili
kontraktu IRS w chwili ![]() ma rozkład log-normalny taki, że
ma rozkład log-normalny taki, że
-
odchylenie standardowe
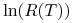 wynosi
wynosi 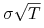 ,
, -
wartość oczekiwana stopy
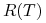 jest równa aktualnie obserwowanej stopie
jest równa aktualnie obserwowanej stopie
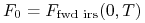 kontraktu forward IRS który zaczynie
się w
kontraktu forward IRS który zaczynie
się w  ,
,
to każdą z ![]() opcji, które dają wypłatę payer's swapcji, można
wycenić wzorem Blacka'76
opcji, które dają wypłatę payer's swapcji, można
wycenić wzorem Blacka'76
| (12.18) |
gdzie
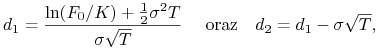 |
(12.19) |
a ![]() jest czynnikiem, który dyskontuje z chwili
jest czynnikiem, który dyskontuje z chwili ![]() na
chwilę bieżącą.
na
chwilę bieżącą.
Tak więc wartość payer's swapcji wynosi
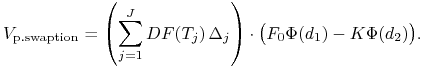 |
(12.20) | ||
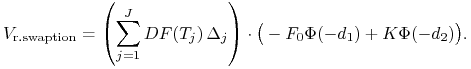 |
Wzory (12.20) możemy, podobnie jak w przypadku poprzednio
omawianych opcji, zapisać jedną formułą – mianowicie wartość
payer's (![]() / receiver's (
/ receiver's (![]() swapcji dana jest
wzorem
swapcji dana jest
wzorem
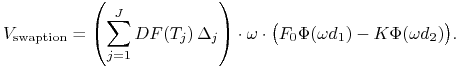 |
(12.21) |
Stopę kontraktu forward IRS, który zacznie się w chwili ![]() i
skończy się w
i
skończy się w ![]() , obserwowaną w chwili wyceny swapcji obliczamy
następującym wzorem:
, obserwowaną w chwili wyceny swapcji obliczamy
następującym wzorem:
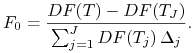 |
(12.22) |
Rynek kwotuje swapcje dla głównych walut (USD, EUR, GBP, JPY)
podając wartości zmienności ![]() , które wstawione do formuł
Blacka'76 prowadzą do ceny gotówkowej. Kwotuje się głównie swapcje
ATM, to znaczy swapcje z cenami wykonania równymi stopom
odpowiednich kontraktów forward IRS.
, które wstawione do formuł
Blacka'76 prowadzą do ceny gotówkowej. Kwotuje się głównie swapcje
ATM, to znaczy swapcje z cenami wykonania równymi stopom
odpowiednich kontraktów forward IRS.
12.7. Niespójność modelu Blacka'76
Model Blacka'76 zakłada, że instrument podstawowy opcji w chwili wygaśnięcia opcji ma rozkład log-normalny. W przypadku
-
wyceny capów / floorów model zakłada, że stopy forward mają rozkład log-normalny,
-
wyceny swapcji model zakłada, że stopy kontraktów IRS mają rozkład log-normalny.
Te dwa założenia są wzajemnie niespójne (sprzeczne), bowiem, jak wiemy (patrz Wykład 4), stopa kontraktu IRS jest w przybliżeniu średnia arytmetyczną stóp forward i jeśli te ostatnie mają rozkład log-normalny, to, na ogół, rozkład stopy kontraktu IRS nie jest log-normalny.
12.8. Finansowe produkty strukturalne z wbudowanymi opcjami na stopę procentową
Kredyt o zmiennej ale ograniczonej z góry stopie procentowej
Rozpatrzmy kredyt, w którym kredytobiorca płaci co ustalony okres
(na przykład co 3M) odsetki obliczone według zmiennej stopy rynkowej
typu LIBOR. Kredytobiorca chce ograniczyć z góry koszt tego kredytu
(efektywnie płaconą stopę od pożyczonego kapitału). Niech ![]() oznacza maksymalny poziom stopy rynkowej jaki chce on zaakceptować.
W tym celu kupuje capa z ceną wykonania
oznacza maksymalny poziom stopy rynkowej jaki chce on zaakceptować.
W tym celu kupuje capa z ceną wykonania ![]() o strukturze zgodnej z
zaciągniętym kredytem (caplety maja czas trwania taki sam jak okresy
odsetkowe kredytu) z nominałem identycznym jak kwota pożyczonego
kapitału. Zawarty kontrakt cap będzie rekompensował kredytobiorcy
potencjalnie wyższe koszty obsługi kredytu. Niech
o strukturze zgodnej z
zaciągniętym kredytem (caplety maja czas trwania taki sam jak okresy
odsetkowe kredytu) z nominałem identycznym jak kwota pożyczonego
kapitału. Zawarty kontrakt cap będzie rekompensował kredytobiorcy
potencjalnie wyższe koszty obsługi kredytu. Niech ![]() będzie ceną tego capa (na jednostkę nominału). Aby zobaczyć jaki
jest efektywny koszt tego kredytu z uwzględnieniem zabezpieczenia,
rozkładamy koszt capa na strumień dodatkowych płatności płaconych
razem z odsetkami od kredytu. Ten strumień wyrazimy w postaci marży
będzie ceną tego capa (na jednostkę nominału). Aby zobaczyć jaki
jest efektywny koszt tego kredytu z uwzględnieniem zabezpieczenia,
rozkładamy koszt capa na strumień dodatkowych płatności płaconych
razem z odsetkami od kredytu. Ten strumień wyrazimy w postaci marży
![]() powyżej płaconej stopy, a więc kredytobiorca płaci
powyżej płaconej stopy, a więc kredytobiorca płaci
LIBOR![]() jeżeli LIBOR
jeżeli LIBOR![]()
lub ![]() jeżeli LIBOR
jeżeli LIBOR![]() .
.
Jeżeli wystawcą capa jest kredytodawca, to istotnie, zamiast
przyjmować premię za capa w chwili zawierania umowy, może on
rozłożyć premię capa na strumień płatności marżowych, które będzie
otrzymywał razem z odsetkami. Wielkość marży ![]() spełnia równanie
spełnia równanie
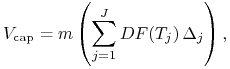 |
(12.23) |
gdzie ![]() jest długością
jest długością ![]() -tego okresu odsetkowego kredytu
(czasu trwania
-tego okresu odsetkowego kredytu
(czasu trwania ![]() -tego capletu), a
-tego capletu), a ![]() są terminami płatności
odsetkowych. Tak obliczona marża
są terminami płatności
odsetkowych. Tak obliczona marża ![]() jest funkcją poziomu
zabezpieczenia
jest funkcją poziomu
zabezpieczenia ![]() .
.
Musimy obsłużyć jeszcze mały niuans. Jak wiemy, konstrukcja capa
zakłada, że pierwszy caplet zaczyna się od pierwszego
przyszłego okresu depozytowego (odsetkowego) stopy, która
jest instrumentem podstawowym capa, czyli że bieżący okres
nie jest objęty zabezpieczeniem. Wówczas, aby usunąć to
niedopasowanie między strukturą kredytu a strukturą capa, do
struktury capa dołącza się dodatkowego capleta na ten pierwszy
bieżący okres o znanym już rozliczeniu, którego wartość
bieżąca włącza się do ceny capa. Dalej, marżę ![]() obliczmy z wzoru
(12.23), gdzie w cenie capa po lewej stronie uwzględniono
wartość bieżącą rozliczenia dodatkowego początkowego capleta.
obliczmy z wzoru
(12.23), gdzie w cenie capa po lewej stronie uwzględniono
wartość bieżącą rozliczenia dodatkowego początkowego capleta.
Należy jeszcze zwrócić uwagę na fakt, że opisując powyższą strukturę zabezpieczania kredytu zakładaliśmy, że caplety wchodzące w skład tej struktury dają (niezdyskontowane stopą LIBOR) wypłaty na końcu okresów depozytowych stopy LIBOR, a nie na początku, jak to opisaliśmy w (12.1). Ta modyfikacja capa nie wpływa na wycenę capa ani obliczenie marży.
Inverse floating rate note (reverse floater, bull floating rate note)
Inverse floater to papier wartościowy który płaci kupony liczone według stopy
| (12.24) |
gdzie ![]() jest ustalonym poziomem stopy procentowej, zwykle w chwili
emisji papieru istotnie większym niż bieżący poziom stóp rynkowych
LIBOR, z dodatkowym warunkiem, że stopa (12.24) nie może
stać się ujemna – to znaczy w takiej sytuacji kupon jest zerowy.
Jakie instrumenty pochodne są wbudowane w tą strukturę?
jest ustalonym poziomem stopy procentowej, zwykle w chwili
emisji papieru istotnie większym niż bieżący poziom stóp rynkowych
LIBOR, z dodatkowym warunkiem, że stopa (12.24) nie może
stać się ujemna – to znaczy w takiej sytuacji kupon jest zerowy.
Jakie instrumenty pochodne są wbudowane w tą strukturę?
Range accrual note
Range accrual note to papier wartościowy który płaci kupon liczony według stopy obliczonej następującym algorytmem
| (12.25) |
gdzie
-
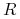 jest z góry ustaloną stopą tego papieru (ta stopa może być różna dla różnych okresów odsetkowych),
jest z góry ustaloną stopą tego papieru (ta stopa może być różna dla różnych okresów odsetkowych), -
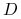 jest liczbą dni handlowych w okresie odsetkowym,
jest liczbą dni handlowych w okresie odsetkowym, -
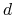 jest liczbą dni tego okresu odsetkowego
w których stopa LIBOR miała wartość w ustalonym zakresie, tzn. kiedy
jest liczbą dni tego okresu odsetkowego
w których stopa LIBOR miała wartość w ustalonym zakresie, tzn. kiedy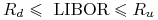
(12.26) dla pewnych ustalonych
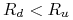 .
.
Jakie instrumenty pochodne są wbudowane w tę strukturę?
Uwaga 12.1
W innym wariancie Range accrual note kupon liczony jest od stopy
| (12.27) |
gdzie
-
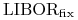 jest stopą LIBOR
ustaloną na początku okresu odsetkowego, niekoniecznie taką samą,
która jest używana do sprawdzania warunku (12.26) celem
wyznaczenia liczby
jest stopą LIBOR
ustaloną na początku okresu odsetkowego, niekoniecznie taką samą,
która jest używana do sprawdzania warunku (12.26) celem
wyznaczenia liczby 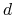 – na przykład, jeśli okresy odsetkowe są
sześciomiesięczne to
– na przykład, jeśli okresy odsetkowe są
sześciomiesięczne to 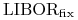 jest
sześciomiesięczną stopą LIBOR, a stopa LIBOR używana w warunku
(12.26) jest stopą trzymiesięczną,
jest
sześciomiesięczną stopą LIBOR, a stopa LIBOR używana w warunku
(12.26) jest stopą trzymiesięczną, -
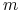 jest marżą addytywną.
jest marżą addytywną.
W tym wariancie wycena jest istotnie trudniejsza niż w wariancie ze stała stopą. Zwykle musimy się posiłkować metodami przybliżonymi, na przykład metodami Monte Carlo wraz z odpowiednio skalibrowanym modelem stóp procentowych.
12.9. Zagadnienia i zadania na Ćwiczenia
Ćwiczenie 12.1
Cena capleta 6x9 z górnym poziomem stopy 5% wynosi 15 bp. Oblicz cenę floorleta 6x9 z dolnym poziomem stopy 5% wiedząc, że stopa 6M LIBOR wynosi 4.5% a kwotowanie FRA6x9 wynosi 5.5%. Dla uproszczenia obliczeń można przyjąć, że stopy są na bazie 30/360.
Ćwiczenie 12.2
Firma wuwu.com może zaciągnąć kredyt na okres 3 lat w którym
będzie płacić półroczne odsetki od pożyczonej kwoty według stopy
rynkowej zmiennej LIBOR plus 150 bp (kwota kredytu będzie spłacona
na końcu). Ponieważ firma wuwu.com chce uchronić się przed
wysokimi kosztami tego kredytu, to jest, nie chce płacić więcej niż
6% w przypadku wzrostu stóp procentowych, bank, w którym firma
zaciąga kredyt, proponuje jej kupno trzyletniego kontraktu cap na
stopę 6M LIBOR. Bieżąca struktura stóp procentowych
(kapitalizowanych w sposób ciągły) jest płaska i stopy te wynoszą
4%. Zmienność trzyletnich kontraktów cap wynosi 20%. Za
wystawienie tej opcji firmie wuwu.com bank zamierza pobrać
opłatę w formie prowizji. Oblicz wartość tej prowizji.
Ćwiczenie 12.3 (IRS z ograniczoną stopą zmienną)
Rozpatrzmy ![]() -letni kontrakt wymiany procentowej, w którym wysokość
stopy zmiennej jest ograniczona z góry. Noga stała płaci odsetki co
rok, a noga zmienna co sześć miesięcy. Odsetki nogi zmiennej (na
jednostkę nominału) za
-letni kontrakt wymiany procentowej, w którym wysokość
stopy zmiennej jest ograniczona z góry. Noga stała płaci odsetki co
rok, a noga zmienna co sześć miesięcy. Odsetki nogi zmiennej (na
jednostkę nominału) za ![]() -ty sześciomiesięczny okres odsetkowy w
tym kontrakcie wynoszą
-ty sześciomiesięczny okres odsetkowy w
tym kontrakcie wynoszą
gdzie
![]() jest 6M stopą rynkową (typu LIBOR) ustalaną na początku okresu
odsetkowego,
jest 6M stopą rynkową (typu LIBOR) ustalaną na początku okresu
odsetkowego, ![]() jest długością tego okresu, a
jest długością tego okresu, a
![]() ustaloną kontraktem maksymalną wartością płaconej
stopy rynkowej. Stopa
ustaloną kontraktem maksymalną wartością płaconej
stopy rynkowej. Stopa ![]() nogi stałej tego kontraktu jest tak
dobierana, by w chwili rozpoczęcia kontraktu wartość kontraktu
wynosiła zero. Oznaczmy ten kontrakt symbolem IRS
nogi stałej tego kontraktu jest tak
dobierana, by w chwili rozpoczęcia kontraktu wartość kontraktu
wynosiła zero. Oznaczmy ten kontrakt symbolem IRS![]() .
.
-
(a) Przedstaw kontrakt IRS
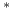 jako portfel złożony pewnego kontraktu IRS
oraz odpowiedniego instrumentu pochodnego.
jako portfel złożony pewnego kontraktu IRS
oraz odpowiedniego instrumentu pochodnego. -
(b) Wyprowadź formułę na wartość stopy
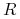 kontraktu IRS
kontraktu IRS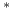 jako funkcję
od stopy
jako funkcję
od stopy 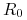 standardowego kontraktu IRS (o takim samym
czasie trwania i takiej samej strukturze okresów odsetkowych jak w
kontrakcie IRS
standardowego kontraktu IRS (o takim samym
czasie trwania i takiej samej strukturze okresów odsetkowych jak w
kontrakcie IRS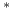 ), ceny odpowiedniego instrumentu pochodnego
(patrz (a)), bieżącej wartości
), ceny odpowiedniego instrumentu pochodnego
(patrz (a)), bieżącej wartości 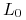 sześciomiesięcznej stopy
rynkowej oraz bieżącej wartości
sześciomiesięcznej stopy
rynkowej oraz bieżącej wartości 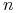 -letniej zerokuponowej stopy
procentowej
-letniej zerokuponowej stopy
procentowej 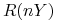 .
.
-
(c) Wykonaj obliczenia dla następujących danych liczbowych:
-
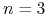 (to jest dla trzyletniego kontraktu),
(to jest dla trzyletniego kontraktu), -
stopa standardowego kontraktu IRS 3Y
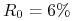 ,
, -
6M stopa (typu LIBOR)
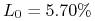 ,
, -
górny poziom stopy
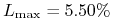 ,
, -
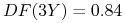 ,
, -
caps (ceny w bp, dla danych cen wykonania)
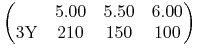
-
floors (ceny w bp, dla danych cen wykonania)

-
Ćwiczenie 12.4
Bieżąca struktura stóp procentowych (kapitalizowanych w sposób ciągły) jest płaska i stopy te wynoszą 5%.
-
(a) Oblicz stopę
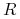 pięcioletniego kontraktu IRS o rocznych okresach odsetkowych nogi stałej.
pięcioletniego kontraktu IRS o rocznych okresach odsetkowych nogi stałej. -
(b) Oblicz premię, którą Bank powinien pobrać od klienta zawierającego z Bankiem kontrakt wymiany procentowej IRS, w którym Bank będzie płacił stałą stopę w wysokości
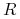 (obliczoną w punkcie
(a)) rocznie przez 5 lat, za danie klientowi możliwości
bezkosztowego
(obliczoną w punkcie
(a)) rocznie przez 5 lat, za danie klientowi możliwości
bezkosztowego-
(i) przerwania kontraktu po 3 latach,
-
(ii) wydłużenia kontraktu w terminie zapadalności z tą samą stopą o kolejne 2 lata.
-
Przyjmij, że zmienność swapcji wynosi 20% niezależnie od terminu zapadalności i tenoru kontaktu swap, który jest instrumentem podstawowym swapcji.
Ćwiczenie 12.5
Oblicz cenę trzyletniej opcji kupna po cenie nominalnej pięcioletniej obligacji, która będzie płacić rocznie kupon w wysokości 5%. Bieżąca struktura stóp procentowych (kapitalizowanych w sposób ciągły) jest płaska i stopy te wynoszą 5%. Przyjmij, że zmienność trzyletnich swapcji wynosi 20% niezależnie od tenoru kontaktu swap, który jest instrumentem podstawowym swapcji.




