Zagadnienia
5. Kontrakty Forward i Futures
5.1. Struktura kontraktów Forward
Kontrakt Forward to umowa kupna / sprzedaży pewnego aktywa (np. akcji, waluty, papieru wartościowego, towaru, etc.)
-
w ustalonym umową terminie (data zapadalności kontraktu)
 ,
, -
po ustalonej umową cenie (cena wykonania)
 .
.
Główny obrót kontraktami Forward odbywa się na rynku nieregulowanym (OTC – ang. Over The Counter) i w związku z tym te kontrakty nie są wystandaryzowane. Warunki kontraktu, w szczególności nominał kontraktu (ilość aktywa będącego przedmiotem umowy), data zapadalności kontraktu, oraz sposób jego rozliczenia, są dopasowywane do potrzeb stron kontraktu (uzgadniane między stronami kontraktu).
Kontrakt Forward jest zawierany z ceną wykonania ![]() , która jest
dobrana tak by w chwili zawarcia kontraktu
, która jest
dobrana tak by w chwili zawarcia kontraktu ![]() jego
wartość wynosiła zero. Tak więc przy założeniu, że pomijamy wszelkie
dodatkowe opłaty związane z transakcją (np. prowizje pośredników),
strony kontraktu Forward nie ponoszą kosztów w chwili jego zawarcia.
jego
wartość wynosiła zero. Tak więc przy założeniu, że pomijamy wszelkie
dodatkowe opłaty związane z transakcją (np. prowizje pośredników),
strony kontraktu Forward nie ponoszą kosztów w chwili jego zawarcia.
Strona kontraktu Forward, która
-
,,kupi” aktywo w terminie zapadalności
 , zajmuje długą
pozycję w tym kontrakcie;
, zajmuje długą
pozycję w tym kontrakcie; -
,,sprzeda” aktywo w terminie zapadalności
 , zajmuje krótką
pozycję w tym kontrakcie.
, zajmuje krótką
pozycję w tym kontrakcie.
Realizacja kontraktu Forward w terminie zapadalności ![]() następuje
przez:
następuje
przez:
fizyczną dostawę aktywa – strona krótka dostarcza aktywo stronie długiej i otrzymuje od niej ustaloną umową kwotę pieniędzy
albo przez
rozliczenie gotówkowe – strona która traci na kontrakcie płaci drugiej stronie kwotę rozliczenia (taki kontrakt określa się często symbolem NDF od ang. NonDeliverable Forward).
Wynik z kontraktu Forward w terminie zapadalności ![]() dla
strony, która przyjęła długą pozycję wynosi
dla
strony, która przyjęła długą pozycję wynosi
| (5.1) |
gdzie ![]() jest ceną aktywa w chwili
jest ceną aktywa w chwili ![]() .
. ![]() jest kwotą
rozliczenia kontraktu w przypadku kontraktu realizowanego przez
rozliczenie gotówkowe. W przypadku kontraktu realizowanego przez
dostawę, taki sam wynik może zrealizować strona długa kontraktu
przez natychmiastową w chwili
jest kwotą
rozliczenia kontraktu w przypadku kontraktu realizowanego przez
rozliczenie gotówkowe. W przypadku kontraktu realizowanego przez
dostawę, taki sam wynik może zrealizować strona długa kontraktu
przez natychmiastową w chwili ![]() sprzedaż po cenie
sprzedaż po cenie ![]() dostarczonego aktywa.
dostarczonego aktywa.
Cena wykonania kontraktu Forward
Opiszemy cenę wykonania dla kilku charakterystycznych typów aktywów
-
dla aktywa które daje posiadaczowi przychód pieniężny w z góry ustalonych wysokościach i chwilach czasu,
-
dla aktywa które daje posiadaczowi ciągły przychód pieniężny wyrażony stopą kapitalizowaną w sposób ciągły,
-
w szczególnym przypadku walutowych kontraktów Forward.
Cena wykonania jest wyliczana tak, by wartość kontraktu w chwili
jego zawarcia wynosiła zero. Tak wyliczoną cenę wykonania kontraktu
Forward nazywamy ceną forward aktywa na dzień ![]() i wtedy
oznaczamy ją symbolem
i wtedy
oznaczamy ją symbolem ![]() , a gdy zachodzi potrzeba zaznaczenia
zależności od
, a gdy zachodzi potrzeba zaznaczenia
zależności od ![]() symbolem
symbolem ![]() .
.
Dla uproszczenia notacji przyjmijmy że ![]() . W
poniższych wzorach
. W
poniższych wzorach ![]() oznacza krzywą czynników
dyskontowych dla waluty w której denominowane jest aktywo
obowiązującą w dniu zawarcia kontraktu
oznacza krzywą czynników
dyskontowych dla waluty w której denominowane jest aktywo
obowiązującą w dniu zawarcia kontraktu ![]() dyskontujących do daty dostawy (zwykle do daty spot) dla transakcji
kupna/sprzedaży tego aktywa zawieranej chwili
dyskontujących do daty dostawy (zwykle do daty spot) dla transakcji
kupna/sprzedaży tego aktywa zawieranej chwili ![]() .
.
![]() Aktywo daje posiadaczowi przychód pieniężny w
z góry ustalonych wysokościach i chwilach czasu.
Aktywo daje posiadaczowi przychód pieniężny w
z góry ustalonych wysokościach i chwilach czasu.
Niech ![]() oznacza przepływ pieniężny następujący w chwili
oznacza przepływ pieniężny następujący w chwili ![]() , gdzie
, gdzie ![]() , generowany przez dane aktywo. Na przykład,
gdy rozpatrywanym aktywem jest
, generowany przez dane aktywo. Na przykład,
gdy rozpatrywanym aktywem jest
-
obligacja o stałym oprocentowaniu,
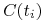 są kuponami które
obligacja płaci jej posiadaczowi;
są kuponami które
obligacja płaci jej posiadaczowi; -
akcja,
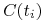 są dywidendami płaconymi przez tą akcję.
są dywidendami płaconymi przez tą akcję.
Wówczas, cena wykonania kontraktu Forward wynosi
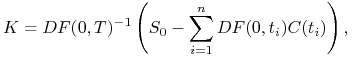 |
(5.2) |
gdzie ![]() jest ceną aktywa w chwili zawarcia kontraktu.
jest ceną aktywa w chwili zawarcia kontraktu.
Uzasadnienie wzoru (5.2). Aby żadna ze stron kontraktu nie
mogła przeprowadzić transakcji arbitrażowej używając, między innymi,
kontraktu Forward z ceną wykonania ![]() , cena bieżąca aktywa musi być
równa sumie wartości bieżących przepływów generowanych przez to
aktywo w czasie trwania kontraktu i bieżącej wartości ceny wykonania
, cena bieżąca aktywa musi być
równa sumie wartości bieżących przepływów generowanych przez to
aktywo w czasie trwania kontraktu i bieżącej wartości ceny wykonania
![]() . Zatem
. Zatem
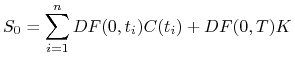 |
skąd po
przekształceniu otrzymujemy wzór (5.2). Przypuśćmy, że
równość (5.2) nie zachodzi. Na przykład, rozpatrzmy
przypadek gdy ![]() jest większe niż prawa strona (5.2).
Pokażemy, że wówczas można przeprowadzić następującą transakcję
arbitrażową:
jest większe niż prawa strona (5.2).
Pokażemy, że wówczas można przeprowadzić następującą transakcję
arbitrażową:
-
zajmujemy krótką pozycję w kontrakcie Forward z ceną
 ,
, -
w chwili zawarcia kontraktu Forward, pożyczamy na okres czasu
![[0,T]](wyklady/ifi/mi/mi591.png) sumę równą aktualnej wartości aktywa
sumę równą aktualnej wartości aktywa 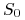 po stopie
po stopie
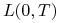 ,
, -
za
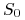 kupujemy na rynku natychmiastowym jednostkę aktywa,
kupujemy na rynku natychmiastowym jednostkę aktywa, -
zawieramy serię transakcji na przyszłą stopę procentową (FRA) dla okresów
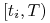 (ze stopami
(ze stopami 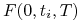 ), które zagwarantują
ulokowanie dochodów
), które zagwarantują
ulokowanie dochodów 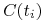 na okres
na okres 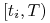 po tych stopach.
po tych stopach.
W chwili wygaśnięcia ![]() kontraktu Forward nasz bilans wygląda
następująco:
kontraktu Forward nasz bilans wygląda
następująco:
-
płacimy sumę
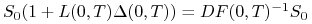 jako
zwrot zaciągniętej pożyczki,
jako
zwrot zaciągniętej pożyczki, -
otrzymujemy kwoty
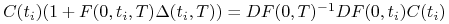 , jako wypłaty ze zrobionych lokat,
, jako wypłaty ze zrobionych lokat, -
otrzymujemy
 za dostarczenie aktywa drugiej stronie kontraktu
Forward,
za dostarczenie aktywa drugiej stronie kontraktu
Forward,
czyli netto otrzymamy
zgodnie z przyjętym założeniem. Mamy więc zysk bez ryzyka. Wówczas, działania arbitrażystów szybko doprowadzają do obniżenia ceny kontraktu Forward do poziomu, który nie daje możliwości bezryzykownego zysku.
W drugim przypadku, to jest, gdy cena kontraktu Forward jest niższa niż prawa strona (5.2), przeprowadzamy transakcję arbitrażową, która jest ,,odwróceniem” strategii wykonanej w poprzednim przypadku:
-
zajmujemy długą pozycję w kontrakcie Forward z ceną
 ,
, -
dokonujemy ,,krótkiej” sprzedaży jednostki aktywa,
-
po sprzedaży aktywa, sumę
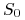 otrzymaną ze sprzedaży
składamy na depozycie na okres czasu
otrzymaną ze sprzedaży
składamy na depozycie na okres czasu ![[0,T]](wyklady/ifi/mi/mi591.png) ze stopą
ze stopą 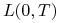 ,
, -
zawieramy serię transakcji na przyszłą stopę procentową (FRA) dla okresów
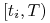 (ze stopami
(ze stopami 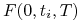 ), które zagwarantują
nam pożyczanie na okres
), które zagwarantują
nam pożyczanie na okres 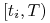 po tych stopach kwot
po tych stopach kwot 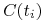 ,
które musimy wypłacić właścicielowi aktywa.
,
które musimy wypłacić właścicielowi aktywa.
Łatwo sprawdzić że, przy naszym założeniu, ta strategia przynosi zysk. Znów mamy arbitraż.
![]() Aktywo daje posiadaczowi ciągły przychód
pieniężny wyrażony stopą kapitalizowaną w sposób ciągły.
Aktywo daje posiadaczowi ciągły przychód
pieniężny wyrażony stopą kapitalizowaną w sposób ciągły.
Podstawowym przykładem takiego aktywa jest akcja (indeks giełdowy), która płaci ciągłą dywidendę, bądź gotówka w walucie obcej.
Niech ![]() oznacza stopę dochodu (dywidendy) płaconego przez aktywo
(akcję). Załóżmy, że otrzymywany dochód jest natychmiast w sposób
ciągły reinwestowany w to samo aktywo. Wówczas ilość posiadanego
aktywa w chwili
oznacza stopę dochodu (dywidendy) płaconego przez aktywo
(akcję). Załóżmy, że otrzymywany dochód jest natychmiast w sposób
ciągły reinwestowany w to samo aktywo. Wówczas ilość posiadanego
aktywa w chwili ![]() wynosi
wynosi ![]() , gdzie
, gdzie ![]() jest ilością aktywa w
jest ilością aktywa w ![]() , a
, a ![]() długością okresu czasu od
chwili początkowej do
długością okresu czasu od
chwili początkowej do ![]() obliczoną zgodnie z konwencją stopy
obliczoną zgodnie z konwencją stopy ![]() .
Pokażemy, że cena kontraktu Forward, który zapada w chwili
.
Pokażemy, że cena kontraktu Forward, który zapada w chwili ![]() , na
aktywo dające ciągły dochód ze stopą
, na
aktywo dające ciągły dochód ze stopą ![]() wynosi
wynosi
| (5.3) |
Aby uzasadnić (5.3), znów rozpatrujemy dwa przypadki –
kiedy ![]() jest większe lub mniejsze niż prawa strona (5.3)
– pokazując, że w każdym z nich możemy skonstruować odpowiednie
strategie arbitrażowe.
jest większe lub mniejsze niż prawa strona (5.3)
– pokazując, że w każdym z nich możemy skonstruować odpowiednie
strategie arbitrażowe.
Gdy ![]() jest większe niż prawa strona (5.3), przeprowadzamy
w chwili początkowej następujące transakcje:
jest większe niż prawa strona (5.3), przeprowadzamy
w chwili początkowej następujące transakcje:
-
zajmujemy krótką pozycję w kontrakcie Forward z ceną
 ,
, -
w chwili zawarcia kontraktu Forward, pożyczamy na okres czasu
![[0,T]](wyklady/ifi/mi/mi591.png) sumę równą
sumę równą 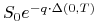 po stopie
po stopie 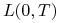 ,
, -
kupujemy na rynku natychmiastowym
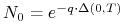 ,,jednostek” aktywa za kwotę
,,jednostek” aktywa za kwotę
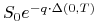 ,
, -
dochody generowane przez aktywo w sposób ciągły reinwestujemy w aktywo.
W rezultacie w chwili wygaśnięcia kontraktu Forward bilans naszych transakcji wygląda następująco
-
płacimy sumę
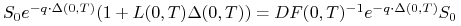 jako zwrot zaciągniętej
pożyczki,
jako zwrot zaciągniętej
pożyczki, -
posiadamy dokładnie jedną jednostkę aktywa (bo
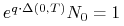 ), za którą
), za którą -
otrzymujemy
 po dostarczeniu jej drugiej stronie kontraktu
Forward.
po dostarczeniu jej drugiej stronie kontraktu
Forward.
Tak więc mamy
czyli uzyskaliśmy zysk bez ryzyka.
W drugim przypadku, gdy ![]() jest mniejsze niż prawa strona
(5.3), przeprowadzamy transakcje w ,,przeciwną” stronę w
stosunku do transakcji przeprowadzonych w poprzedniej sytuacji
(
jest mniejsze niż prawa strona
(5.3), przeprowadzamy transakcje w ,,przeciwną” stronę w
stosunku do transakcji przeprowadzonych w poprzedniej sytuacji
(![]() Zadanie na Ćwiczenia).
Zadanie na Ćwiczenia).
![]() Cena wykonania walutowych kontraktów Forward
(aktywem jest waluta).
Cena wykonania walutowych kontraktów Forward
(aktywem jest waluta).
Walutowy kontrakt Forward = FX forward = Outright Forward
Walutę, oznaczmy ją przez ![]() , możemy potraktować jak
aktywo, które płaci dochód w postaci odsetek, które narastają na
rachunku oprocentowanym stopą dla tej waluty. Jeśli bowiem posiadamy
gotówkę w tej walucie, to możemy ją zdeponować na rachunku walutowym
i w ten sposób otrzymywać dochód z tytułu posiadania waluty.
Oprocentowanie tego rachunku możemy wyrazić przez stopę
kapitalizowaną w sposób ciągły i wtedy walutę możemy uznać za
aktywo, które płaci dochód w sposób ciągły ze stopą
, możemy potraktować jak
aktywo, które płaci dochód w postaci odsetek, które narastają na
rachunku oprocentowanym stopą dla tej waluty. Jeśli bowiem posiadamy
gotówkę w tej walucie, to możemy ją zdeponować na rachunku walutowym
i w ten sposób otrzymywać dochód z tytułu posiadania waluty.
Oprocentowanie tego rachunku możemy wyrazić przez stopę
kapitalizowaną w sposób ciągły i wtedy walutę możemy uznać za
aktywo, które płaci dochód w sposób ciągły ze stopą ![]() . Ceną
natychmiastową
. Ceną
natychmiastową ![]() waluty
waluty ![]() jest jej kurs wymiany na
drugą walutę
jest jej kurs wymiany na
drugą walutę ![]() (kwotowany jako ilość
(kwotowany jako ilość ![]() za
jednostkę
za
jednostkę ![]() ). Wówczas cenę walutowego kontraktu
Forward, w którym wymieniamy walutę
). Wówczas cenę walutowego kontraktu
Forward, w którym wymieniamy walutę ![]() na drugą walutę
na drugą walutę
![]() (na przykład na PLN), otrzymamy ze wzoru
(5.3), w którym
(na przykład na PLN), otrzymamy ze wzoru
(5.3), w którym
-
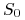 jest kursem wymiany natychmiastowej (spot)
jest kursem wymiany natychmiastowej (spot) 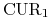 na
na
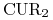 ,
, -
stopa dochodu
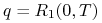 jest stopą
kapitalizowaną w sposób ciągły waluty
jest stopą
kapitalizowaną w sposób ciągły waluty 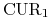 ,
, -
a czynnik dyskontowy odpowiada krzywej dla waluty
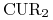 .
.
Czynnik dyskontowy ![]() dla waluty
dla waluty ![]() możemy
zapisać w postaci
możemy
zapisać w postaci
gdzie ![]() jest stopą kapitalizowaną w sposób ciągły dla
okresu
jest stopą kapitalizowaną w sposób ciągły dla
okresu ![]() (dla waluty
(dla waluty ![]() ). Wówczas, wzór na cenę
walutowego kontraktu Forward przyjmuje następującą formę
). Wówczas, wzór na cenę
walutowego kontraktu Forward przyjmuje następującą formę
| (5.4) |
Zwykle, wzór na cenę walutowego kontraktu Forward podaje się w
postaci w której występują stopy proste ![]() i
i ![]() (bo
takie stopy są standardem kwotowania na rynku terminowych transakcji
walutowych):
(bo
takie stopy są standardem kwotowania na rynku terminowych transakcji
walutowych):
| (5.5) |
Wzory (5.4) i (5.5) określają tak zwany,
kurs terminowy wymiany walut ![]() ,
który zwykle oznaczamy symbolem
,
który zwykle oznaczamy symbolem ![]() . Upraszczając notację wzór na
kurs terminowy napiszemy w następujący sposób
. Upraszczając notację wzór na
kurs terminowy napiszemy w następujący sposób
| (5.6) |
Związek (5.6) jest określany również jako tzw. parytet stóp procentowych. Z (5.6) wynika, że
| (5.7) |
co możemy
zinterpretować w następujący sposób: taki sam wynik w ![]() uzyskamy
uzyskamy
-
(a) wymieniając jednostkę waluty
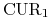 po kursie natychmiastowym na
po kursie natychmiastowym na
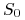 waluty
waluty 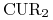 i lokując tę kwotę po stopie
i lokując tę kwotę po stopie 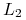 na
okres
na
okres 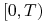 (lewa strona (5.7)),
(lewa strona (5.7)),
albo
-
(b) lokując jednostkę waluty
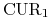 kwotę po stopie
kwotę po stopie 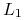 na okres
na okres 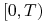 i w
i w  wymieniając kwotę
wymieniając kwotę 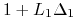 waluty
waluty 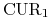 po
kursie terminowym
po
kursie terminowym 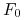 na walutę
na walutę 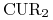 (prawa strona
(5.7)).
(prawa strona
(5.7)).
Punkty swapowe to różnica między kursem terminowym a kursem spotowym:
| (5.8) |
Gdy ![]() , z (5.8) wynika, że
, z (5.8) wynika, że
co po przepisaniu do postaci
oznacza iż
zannualizowana stopa zwrotu na transakcji kupna waluty
![]() w t=0 po
w t=0 po ![]() i jej sprzedaży po
i jej sprzedaży po ![]() w
w ![]() jest
równa różnicy w oprocentowaniu walut.
jest
równa różnicy w oprocentowaniu walut.
Aspekty praktyczne dotyczące transakcji FX forward
-
Kursy FX forward są kwotowane przez animatorów rynku (ang. market makers) dla standardowych okresów depozytowych, zwykle do 1Y.
-
Kursy FX forward są kwotowane w postaci punktów swapowych, wyrażonych w tak zwanych pipsach, czyli w
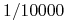 waluty niebazowej. Aby
uzyskać faktyczny kurs FX forward dla terminów ,,powyżej” spot
należy do bieżącego kursu spot dodać (z właściwym znakiem)
odpowiednio przeskalowane punkty swapowe, przy czym należy pamiętać,
że punkty swapowe mogą być zarówno dodatnie jak i ujemne.
waluty niebazowej. Aby
uzyskać faktyczny kurs FX forward dla terminów ,,powyżej” spot
należy do bieżącego kursu spot dodać (z właściwym znakiem)
odpowiednio przeskalowane punkty swapowe, przy czym należy pamiętać,
że punkty swapowe mogą być zarówno dodatnie jak i ujemne. -
Rynek kwotuje również punkty swapowe dla okresów ON i TN. Wówczas obliczając kursy wymiany dla tych terminów należy punkty swapowe odejmować (z właściwym znakiem) od kursu spot.
-
Punkty swapowe są kwotowane w postaci pary
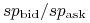 gdzie
gdzie 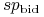 (
(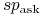 ) są punktami swapowymi
dla transakcji FX forward w której kupujemy (sprzedajemy) walutę
bazową.
) są punktami swapowymi
dla transakcji FX forward w której kupujemy (sprzedajemy) walutę
bazową. -
Jeżeli punkty swapowe są dodatnie, to
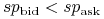 .
Zdarza się, że ujemne punkty swapowe są kwotowane bez znaku i wtedy
w kwotowanej parze
.
Zdarza się, że ujemne punkty swapowe są kwotowane bez znaku i wtedy
w kwotowanej parze 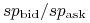 będziemy mieli
nierówność przeciwną
będziemy mieli
nierówność przeciwną 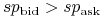 . Wówczas,
po tej relacji rozpoznajemy czy punkty swapowe są dodatnie czy
ujemne.
. Wówczas,
po tej relacji rozpoznajemy czy punkty swapowe są dodatnie czy
ujemne.
Replikacja kontraktu FX forward
Pokażemy jak można zreplikować kontrakt FX forward przy pomocy
-
pożyczenia jednej waluty,
-
natychmiastowej wymiany tej waluty na drugą walutę,
-
lokaty drugiej waluty.
Ta replikacja pokazuje powiązania rynku transakcji wymian walutowych z rynkiem pieniężnym.
Rozpatrzmy kontrakt FX forward, w którym
-
w terminie zapadalności

-
kupimy
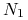 waluty
waluty 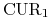 , oraz
, oraz -
sprzedamy
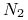 waluty
waluty 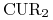 .
.
Oznacza to, że dokonamy wymiany waluty ![]() na walutę
na walutę
![]() po kursie terminowym
po kursie terminowym ![]() takim, że
takim, że ![]() .
.
Efekt wymiany walut w ![]() uzyskamy również w następujący sposób:
uzyskamy również w następujący sposób:
-
pożyczamy na rynku pieniężnym kwotę
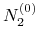 taką by
taką by 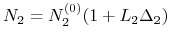 , gdzie
, gdzie 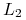 jest
stopą dla udzielonych pożyczek w walucie
jest
stopą dla udzielonych pożyczek w walucie 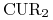 na okres
czasu
na okres
czasu 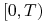 , a
, a 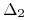 długością tego okresu;
długością tego okresu; -
kwotę
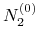 w walucie
w walucie 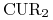 wymieniamy na
wymieniamy na
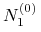 waluty
waluty 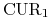 po kursie spot
po kursie spot 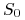 , czyli
, czyli
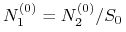 ;
; -
kwotę
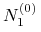 w walucie
w walucie 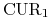 lokujemy
na rynku pieniężnym ze stopą
lokujemy
na rynku pieniężnym ze stopą 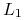 dla przyjętych depozytów w
walucie
dla przyjętych depozytów w
walucie 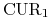 na okres czasu
na okres czasu 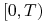 .
.
Rezultatem tych transakcji w chwili ![]() jest
jest
-
zwrot zaciągniętej pożyczki w walucie
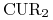 w
kwocie
w
kwocie 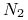 (płacimy
(płacimy 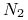 w walucie
w walucie 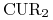 ),
), -
otrzymana wypłata ze złożonego depozytu w walucie
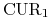 w
kwocie
w
kwocie 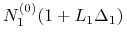 , gdzie
, gdzie 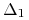 jest długością tego
okresu
jest długością tego
okresu 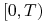 (otrzymujemy
(otrzymujemy 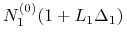 w walucie
w walucie
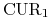 ),
),
czyli dokonujemy wymiany ![]() w waluty
w waluty ![]() na
na
![]() w waluty
w waluty ![]() . Jeśli zatem ta
strategia ma replikować kontrakt FX forward, musi zachodzić równość
. Jeśli zatem ta
strategia ma replikować kontrakt FX forward, musi zachodzić równość
Stąd mamy
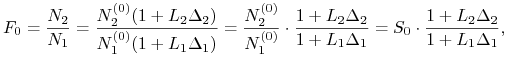 |
czyli znów otrzymaliśmy parytet stóp procentowych. Jeśli ten parytet jest spełniony, replikacja transakcji FX forward zestawem złożonym z dwóch transakcji depozytowych i transakcji wymiany natychmiastowej jest możliwa.
Transakcja FX forward jako FX spot plus FX swap
W wyniku połączenia przepływów pieniężnych transakcji depozytowych, które zostały użyte do replikacji transakcji FX forward, uzyskujemy transakcję FX swap (dokładniej, szczególny przypadek transakcji FX swap). Ta transakcja FX swap, w notacji poprzedniego ustępu, polega na
-
wymianie początkowej (w chwili spot): sprzedaży
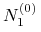 waluty
waluty 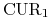 i kupnie
i kupnie 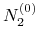 waluty
waluty 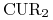 , po kursie spot
, po kursie spot 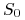 , tzn. tak, aby
, tzn. tak, aby
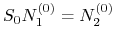 ,
,
oraz
-
wymianie końcowej (w terminie wygaśnięcia): kupnie
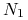 waluty
waluty 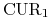 i sprzedaży
i sprzedaży 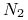 waluty
waluty
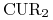 , po kursie po kursie forward
, po kursie po kursie forward 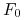 , tzn. tak, aby
, tzn. tak, aby
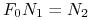 ,
,
przy czym ![]() oraz
oraz
![]() .
.
Jak widać, wymiana początkowa w tej transakcji FX swap znosi się z transakcją FX spot wchodzącą w skład strategii replikującej FX forward. Wówczas z FX swap pozostaje pozostaje tylko wymiana końcowa, która jest oryginalną transakcją FX forward.
Uwagi
-
Reprezentacja FX forward jako suma FX spot i (tego szczególnego) FX swap pozwala na rozdzielenie ryzyk: FX spot ma tylko ryzyko walutowe (ryzyko kursu wymiany walut), a ten FX swap (w chwili początkowej) – tylko ryzyko stopy procentowej.
-
W praktyce rynkowej zawiera się kontrakty FX swap (tzw. round FX swap) w których kwota
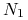 waluty obcej
waluty obcej 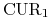 jest taka sama w
wymianie początkowej i wymianie końcowej, a kwoty waluty lokalnej
jest taka sama w
wymianie początkowej i wymianie końcowej, a kwoty waluty lokalnej
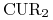 w chwili początkowej i końcowej różnią się ,,punktami
swapowymi” (od nominału
w chwili początkowej i końcowej różnią się ,,punktami
swapowymi” (od nominału 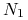 )
)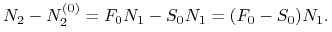
Wycena kontraktu Forward
Rozpatrzmy kontrakt Forward, który został zawarty z ceną wykonania
![]() . W chwili zawarcia kontraktu
. W chwili zawarcia kontraktu ![]() było równe cenie forward aktywa
na które wystawiony został kontrakt. Niech
było równe cenie forward aktywa
na które wystawiony został kontrakt. Niech ![]() oznacza bieżącą (to
jest w chwili wyceny) cenę forward aktywa. Wówczas wycena długiej
pozycji w kontrakcie Forward (jego wartość) dana jest wzorem
oznacza bieżącą (to
jest w chwili wyceny) cenę forward aktywa. Wówczas wycena długiej
pozycji w kontrakcie Forward (jego wartość) dana jest wzorem
| (5.9) |
gdzie ![]() jest terminem zapadalności kontraktu.
jest terminem zapadalności kontraktu.
Uzasadnienie wzoru (5.9). Wartością bieżącą kontraktu
Forward jest wartość bieżąca przepływów pieniężnych w ![]() które
powstałyby w wyniku zamknięcia pozycji w tym kontrakcie. W przypadku
długiej pozycji należałoby zająć pozycję krótką w kontrakcie Forward
na to samo aktywo i z tym samym terminem wykonania
które
powstałyby w wyniku zamknięcia pozycji w tym kontrakcie. W przypadku
długiej pozycji należałoby zająć pozycję krótką w kontrakcie Forward
na to samo aktywo i z tym samym terminem wykonania ![]() co zamykany
kontrakt. Cena wykonania tego zamykającego kontraktu Forward wynosi
co zamykany
kontrakt. Cena wykonania tego zamykającego kontraktu Forward wynosi
![]() i jest określona jednym z wzorów (5.2),
(5.3), (5.4)–(5.5) odpowiednio. W
rezultacie, w chwili
i jest określona jednym z wzorów (5.2),
(5.3), (5.4)–(5.5) odpowiednio. W
rezultacie, w chwili ![]() zapłacilibyśmy
zapłacilibyśmy ![]() za kupione aktywo i
jednocześnie otrzymalibyśmy
za kupione aktywo i
jednocześnie otrzymalibyśmy ![]() w wyniku sprzedaży tego aktywa.
Tak więc, netto nasz wynik w
w wyniku sprzedaży tego aktywa.
Tak więc, netto nasz wynik w ![]() na tych transakcjach wyniósłby
na tych transakcjach wyniósłby
![]() , a jego wartość bieżąca wynosi
, a jego wartość bieżąca wynosi ![]() . Ponieważ
wartość kontraktu Forward (w chwili zawarcia) zamykającego wyceniany
kontrakt wynosi zero, to wartość wycenianego kontraktu Forward jest
równa
. Ponieważ
wartość kontraktu Forward (w chwili zawarcia) zamykającego wyceniany
kontrakt wynosi zero, to wartość wycenianego kontraktu Forward jest
równa ![]() , czyli mamy (5.9).
, czyli mamy (5.9).
Po wstawieniu do (5.9) wyrażeń na cenę forward w poszczególnych przypadkach otrzymujemy następujące formuły na wycenę kontraktów:
![]() Forward na aktywo dające przychód pieniężny w
z góry ustalonych chwilach czasu
Forward na aktywo dające przychód pieniężny w
z góry ustalonych chwilach czasu
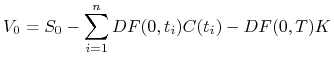 |
(5.10) |
![]() Forward na aktywo dające ciągły przychód
pieniężny wyrażony stopą kapitalizowaną w sposób ciągły
Forward na aktywo dające ciągły przychód
pieniężny wyrażony stopą kapitalizowaną w sposób ciągły
| (5.11) |
![]() FX Forward
FX Forward
| (5.12) |
przy czym wzory te podają wartość kontraktów na jednostkę aktywa (na nominał jednostkowy).
Interpretacja wzoru (5.12) dla transakcji FX forward o
nominale ![]() (waluty
(waluty ![]() ):
):
W wyniku realizacji tego kontraktu dojdzie do wymiany kwoty
(nominału) ![]() w walucie
w walucie ![]() na
na ![]() waluty
waluty
![]() . Zatem, wycena kontraktu FX forward powinna
sprowadzić się do wyceny strumienia przepływów
. Zatem, wycena kontraktu FX forward powinna
sprowadzić się do wyceny strumienia przepływów ![]() i
i ![]() następujących w chwili
następujących w chwili ![]() . Tak jest w istocie, bowiem
. Tak jest w istocie, bowiem
| (5.13) |
Jak widać, ostatnia część wzoru (5.13) jest różnicą dwóch
składowych: pierwsza jest przeliczoną na walutę ![]() po
kursie spotowym
po
kursie spotowym ![]() wartością bieżącą otrzymywanego w
wartością bieżącą otrzymywanego w ![]() nominału
nominału
![]() , a druga (odejmowana) jest wartością bieżącą nominału
, a druga (odejmowana) jest wartością bieżącą nominału ![]() .
.
5.2. Kontrakty Futures
Kontrakty Futures są kontraktami terminowymi kupna/sprzedaży pewnego aktywa (towaru) przy czym w odróżnieniu od kontraktów Forward
-
funkcjonują na rynku uregulowanym – obrót tymi kontraktami odbywa się przez giełdy
-
są produktami wystandaryzowanymi, w tym sensie, że przedmiotem kontraktu są dobrze zdefiniowane aktywa (towary) – ustalone są:
-
ilość aktywa przypadająca na jeden kontrakt,
-
,,jakość” aktywa,
-
warunki dostawy, termin dostawy,
-
termin wygaśnięcia kontraktu,
-
-
są rozliczane w trybie dziennym, przez rachunek zabezpieczający,
-
na ogół nie dochodzi do fizycznej dostawy aktywa w terminie wykonania kontraktu, a kontrakt jest zamykany przez zajęcie pozycji przeciwnej.
Te cechy kontraktów Futures powodują, że w porównaniu do kontraktów Forward, kontrakty Futures
-
mają relatywnie małe ryzyko kredytowe i rozliczeniowe,
-
dla niezbyt odległych terminów zapadalności są instrumentami o dużej płynności.
Główne rodzaje kontraktów Futures:
-
na papiery skarbowe – T-bond Futures,
-
na depozyty (na stopę procentową) – Eurodollar Futures,
-
na indeksy giełdowe – Index Futures,
-
na waluty – Currency Futures,
-
na towary / surowce – Commodity Futures.
Rozliczanie kontraktu Futures dokonywane jest codziennie
przez rachunek zabezpieczający (ang. margin account), na którym
strona kontraktu Futures jest zobowiązana utrzymywać określony przez
giełdę minimalny poziom zdeponowanej gotówki. Na ten rachunek
zabezpieczający wpływają zyski z tytułu dziennego rozliczenia
kontraktu Futures, lub z tego rachunku są pobierane kwoty
odpowiadające stratom poniesionym w wyniku rozliczenia kontraktu.
Kwota dziennego rozliczenia długiej pozycji w kontrakcie Futures,
które następuje na zamknięcie ![]() -tego dnia, wynosi (na jednostkę
aktywa)
-tego dnia, wynosi (na jednostkę
aktywa)
| (5.14) |
gdzie ![]() jest ceną wykonania
kontraktu Futures na zamknięciu dnia
jest ceną wykonania
kontraktu Futures na zamknięciu dnia ![]() . W dniu zawarcia
kontraktu rozliczenie kontraktu jest obliczane na podstawie ceny
kontraktu Futures z jaką został on zawarty oraz ceny tego kontraktu
na zamknięciu dnia, chyba że kontrakt został zamknięty jeszcze tego
samego dnia (wtedy mówimy o tzw. intraday trading) i wtedy
rozliczenie obywa się po cenie faktycznego zamknięcia kontraktu.
Wzór (5.14) jest również wynikiem realizowanym na
zamknięciu w dniu
. W dniu zawarcia
kontraktu rozliczenie kontraktu jest obliczane na podstawie ceny
kontraktu Futures z jaką został on zawarty oraz ceny tego kontraktu
na zamknięciu dnia, chyba że kontrakt został zamknięty jeszcze tego
samego dnia (wtedy mówimy o tzw. intraday trading) i wtedy
rozliczenie obywa się po cenie faktycznego zamknięcia kontraktu.
Wzór (5.14) jest również wynikiem realizowanym na
zamknięciu w dniu ![]() kontraktu otwartego w dniu
kontraktu otwartego w dniu ![]() . W
rezultacie takiego rozliczania kontraktu Futures można przyjąć że na
zamknięcie dnia
. W
rezultacie takiego rozliczania kontraktu Futures można przyjąć że na
zamknięcie dnia ![]() następuje zamknięcie pozycji otwartej na końcu
poprzedniego dnia z ceną
następuje zamknięcie pozycji otwartej na końcu
poprzedniego dnia z ceną ![]() i jednoczesne otwarcie kontraktu
Futures z ceną
i jednoczesne otwarcie kontraktu
Futures z ceną ![]() . Oczywiście rozliczenie za ostatni dzień
trzymania otwartej pozycji w kontrakcie Futures odbywa się po cenie
faktycznego zamknięcia kontraktu w tym dniu.
. Oczywiście rozliczenie za ostatni dzień
trzymania otwartej pozycji w kontrakcie Futures odbywa się po cenie
faktycznego zamknięcia kontraktu w tym dniu.
Teoretyczna cena kontraktu Futures jest równa cenie wykonania kontraktu Forward na to samo aktywo z tym samym terminem wykonania. W przypadkach gdy termin dostawy kontraktu Futures i dostarczane aktywo są jednoznacznie określone, można próbować porównywać rynkowe ceny Futures z ich cenami teoretycznymi, czyli z cenami forward aktywa na które te kontrakty opiewają. W przypadku kontraktów Futures, w których strona krótka ma możliwości wyboru terminu dostawy (w pewnym zakresie) oraz wyboru dostarczanego aktywa z grupy aktywów dopuszczonych do dostarczania, takie porównanie jest często utrudnione. Przykładem takiego kontraktu jest kontrakt Futures na papiery skarbowe (T-bond Futures).
Pokażemy, że jeżeli
-
stopa procentowa według której oprocentowane są fundusze na rachunku zabezpieczającym jest stała w trakcie trwania kontraktu Futures, a wartość tej stopy jest zgodna z oprocentowaniem lokat/depozytów o czasie trwania
 ,
, -
termin dostawy (wygaśnięcia kontraktu) jest jednoznacznie określony,
-
dostarczane aktywo jest jednoznacznie określone w chwili zawarcia kontraktu,
to teoretyczna cena kontraktu Futures jest równa cenie kontraktu Forward.
Niech
-
 oznacza termin zapadalności kontraktów Futures i Forward,
oznacza termin zapadalności kontraktów Futures i Forward, -
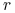 oznacza stałą stopę procentową kapitalizowaną w sposób
ciągły, która będzie stosowana w trakcie trwania kontraktu do
lokowania/finasowania dziennych rozliczeń kontraktu Futures na
rachunku zabezpieczającym – zakładamy, że
oznacza stałą stopę procentową kapitalizowaną w sposób
ciągły, która będzie stosowana w trakcie trwania kontraktu do
lokowania/finasowania dziennych rozliczeń kontraktu Futures na
rachunku zabezpieczającym – zakładamy, że 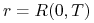 , przy czym
, przy czym
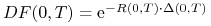 ,
, -
 oznacza cenę kontraktu Forward zawartego na zamknięcie dnia
oznacza cenę kontraktu Forward zawartego na zamknięcie dnia 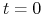 ,
, -
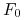 oznacza cenę kontraktu Futures zawartego na zamknięcie dnia
oznacza cenę kontraktu Futures zawartego na zamknięcie dnia 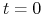 .
.
Czas trwania kontraktów dzielimy na ,,jednodniowe” okresy
![]() , gdzie
, gdzie ![]() , przy czym
, przy czym ![]() a
a ![]() jest dniem zawarcia kontraktu.
jest dniem zawarcia kontraktu.
Rozważmy następującą strategię:
-
sprzedajemy kontrakt Forward na jednostkę aktywa,
-
kupujemy kontrakt Futures na
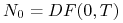 jednostek aktywa, oraz
w każdym dniu
jednostek aktywa, oraz
w każdym dniu 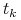 , gdzie
, gdzie  , dokupujemy na jego
zamknięciu taką ilość kontraktów Futures by otwarta pozycja na
rozpoczęciu kolejnego dnia
, dokupujemy na jego
zamknięciu taką ilość kontraktów Futures by otwarta pozycja na
rozpoczęciu kolejnego dnia 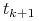 w tym kontrakcie Futures
wynosiła
w tym kontrakcie Futures
wynosiła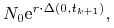
a wynik (rozliczenie) otwartej pozycji na koniec dnia
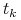 lokujemy/finansujemy ze stopą
lokujemy/finansujemy ze stopą 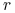 na pozostały do wygaśnięcia
kontraktu okres czasu.
na pozostały do wygaśnięcia
kontraktu okres czasu.
Zawiązanie tej strategii w ![]() nie wiąże się z żadnymi kosztami
początkowymi. Natomiast efekt tej strategii w
nie wiąże się z żadnymi kosztami
początkowymi. Natomiast efekt tej strategii w ![]() jest następujący
jest następujący
-
kontrakt Futures opiewa na dokładnie jedno aktywo, bowiem
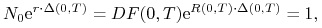
-
w wyniku realizacji kontraktu Futures kupujemy jedno aktywo po cenie
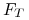 (
(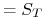 ),
), -
na rachunku zgromadziliśmy (łącznie z odsetkami) kwotę

-
w wyniku realizacji kontraktu Forward dostarczamy jedno aktywo za które otrzymujemy
 .
.
Zatem nasz bilans w ![]() jest następujący:
jest następujący:
Ponieważ strategia prowadząca do tego wyniku nie wiązała się żadnymi kosztami, to by nie było arbitrażu, ten wynik musi być zerowy, czyli musi zachodzić
W rzeczywistości, inwestorzy mogą lokować/finansować wynik dziennego rozliczenia kontraktu Futures po bieżących stopach rynkowych. To, między innymi, powoduje, że w określonych sytuacjach cena kontraktu Futures może odbiegać od ceny odpowiadającego mu kontraktu Forward. Na przykład, gdy cena aktywa, na które jest wystawiony kontrakt Futures, jest mocno dodatnio skorelowana ze stopami procentowymi, inwestor zajmujący długą pozycję może korzystniej lokować bieżące zyski z kontraktu lub odpowiednio taniej finansować straty poniesione na kontrakcie. Tak jest bowiem wzrostowi ceny aktywa, a więc zyskom inwestora, zwykle towarzyszy wzrost stopy procentowej po której może on ulokować swój dochód. Analogicznie, spadek ceny aktywa – strata inwestora – zwykle odbywa się w warunkach spadku stopy procentowej, co oznacza, że inwestor może taniej finansować swoje straty. Tak więc, w takim przypadku, kontrakt Futures jest korzystniejszy dla inwestora niż kontrakt Forward, i w związku z tym cena kontraktu Futures powinna być wyższa niż cena kontraktu Forward. Przeprowadzając podobne rozumowanie, można przypuszczać, że w przypadku gdy cena aktywa jest mocno ujemnie skorelowana ze stopami procentowymi, cena kontraktu Futures powinna być niższa niż cena kontraktu Forward.
3M Eurodollar Futures
Terminologia: Eurodollar – dolar amerykański deponowany w bankach poza USA. Stopa procentowa depozytów eurodolarowych jest utożsamiana ze stopą LIBOR.
-
Giełda: CME (Chicago Mercantile Exchange)
-
Nominał: 1 milion USD
-
Termin zapadalności: trzecia środa miesiąca dostawy
-
Miesiące dostawy: miesiące cyklu marzec, czerwiec, wrzesień, grudzień na około 10 lat naprzód
-
Instrument podstawowy: stopa procentowa 3M USD LIBOR depozytu, który rozpocznie się w dniu zapadalności kontraktu Futures
-
Kwotowanie: cena kontraktu
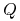 oznacza iż stopa dla odpowiedniego depozytu wynosi
oznacza iż stopa dla odpowiedniego depozytu wynosi
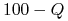 w konwencji ACT/360
w konwencji ACT/360 -
Wartość kontraktu:
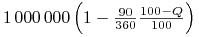 -
mamy tu ,,drobną” niespójność, bowiem, jak widać, przyjęto, że 3M
okres ma 90 dni mimo iż stopa LIBOR jest podawana w konwencji
ACT/360)
-
mamy tu ,,drobną” niespójność, bowiem, jak widać, przyjęto, że 3M
okres ma 90 dni mimo iż stopa LIBOR jest podawana w konwencji
ACT/360) -
Rozliczanie kontraktu: 25 USD za 1 punkt bazowy (0.01 ceny kontraktu); 25 USD = (
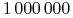 USD
USD 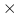 1 bp
1 bp 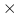 90/360)
90/360)
Są też analogiczne kontrakty Futures na depozyty 3M w innych głównych walutach:
-
Euribor Futures – na 3M EUR LIBOR – giełdy: LIFFE (London International Financial Futures Exchange), MATIF (Marche a Terme International de France),
-
Euroswiss Futures – na 3M CHF LIBOR – giełda: LIFFE
-
Euroyen Futures – na 3M JPY LIBOR – giełdy: CME, SGX (Singapore Exchange Ltd.).
Zagadnienia i zadania na Ćwiczenia
Ćwiczenie 5.1 (Cena forward obligacji)
(a) Cena forward obligacji o stałym kuponie
Przypuśćmy, że rynkowa cena obligacji o stałym kuponie jest zgodna z wyceną modelową, tzn.
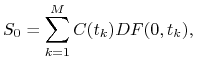 |
gdzie
![]() są wypłatami z tej obligacji (kupony plus ewentualne
częściowe zwroty nominału, oraz końcowa wypłata nominału). Pokaż, że
wówczas wzór na cenę forward tej obligacji można przedstawić w
następującej postaci
są wypłatami z tej obligacji (kupony plus ewentualne
częściowe zwroty nominału, oraz końcowa wypłata nominału). Pokaż, że
wówczas wzór na cenę forward tej obligacji można przedstawić w
następującej postaci
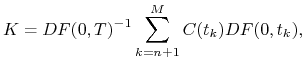 |
gdzie ![]() jest pierwszym momentem
płatności kuponu następującym po terminie wygaśnięcia
jest pierwszym momentem
płatności kuponu następującym po terminie wygaśnięcia ![]() kontraktu
Forward.
kontraktu
Forward.
(b) Cena forward obligacji o zmiennym kuponie
Uzasadnij następujący wzór na cenę forward obligacji o zmiennym kuponie:
gdzie ![]() jest aktualnie pierwszym momentem płatności kuponu tej
obligacji,
jest aktualnie pierwszym momentem płatności kuponu tej
obligacji, ![]() jest długością aktualnie trwającego okresu
odsetkowego, a
jest długością aktualnie trwającego okresu
odsetkowego, a ![]() stopą ustaloną na początku tego okresu, oraz
stopą ustaloną na początku tego okresu, oraz
![]() jest ostatnim przed terminem wygaśnięcia
jest ostatnim przed terminem wygaśnięcia ![]() kontraktu Forward
momentem płatności kuponu. Oczywiście,
kontraktu Forward
momentem płatności kuponu. Oczywiście, ![]() jest aktualną ceną
brudną obligacji. Zakładamy również, że nominał obligacji jest
stały.
jest aktualną ceną
brudną obligacji. Zakładamy również, że nominał obligacji jest
stały.
Ćwiczenie 5.2
Przeprowadź transakcję arbitrażową w przypadku gdy cena kontraktu Forward na aktywo płacące ciągły dochód jest mniejsza niż obserwowana w dniu zawarcia kontraktu cena forward tego aktywa (patrz (5.3)).
Ćwiczenie 5.3
Dane są następujące kwotowania:
-
kurs wymiany USD/PLN: 4.0000,
-
punkty swapowe USD/PLN wynoszą dla 3M: 0.0250, oraz dla 6M: 0.0500,
-
PLN 3M Depo: 4.00%, PLN FRA3x6: 5.00%, USD FRA3x6: 2.00%.
-
(a) Oblicz stopę 3M depozytu dolarowego przy założeniu, że w okresie 3M na rynku nie ma możliwości do arbitrażu.
-
(b) Czy przy powyższych danych istnieją na rynku w okresie do 6M możliwości do arbitrażu? Jeśli tak, opisz strategię arbitrażową i oblicz dzisiejszą wartość wolnego od ryzyka zysku.
Ćwiczenie 5.4 (Kurs bid/ask (kupna/sprzedaży) transakcji FX forward)
Wzory (5.4)–(5.6) na kurs forward zostały wyprowadzone przy założeniu, że stopy procentowe dla przyjętych depozytów i udzielonych pożyczek są takie same. W rzeczywistości stopy te są różne: dla przyjętych depozytów mamy stopy bid, które są niższe niż stopy ask dla udzielonych pożyczek.
Dostosuj wzory (5.4)–(5.6) tak, by wyrażały one wartość kursu bid (ask) transakcji FX forward. Dla przypomnienia terminologii: kurs bid (ask) transakcji wymiany odnosi się do transakcji FX, w której kupujemy (sprzedajemy) walutę bazową (tą, za jednostkę której podajemy ilość waluty niebazowej).
Uwaga: Animator rynku (ang. market maker) kwotuje kurs FX forward w taki sposób, by mógł zapewnić pokrycie swoich zobowiązań z tytułu zawarcia takiej transakcji FX transakcjami na rynku pieniężnym (lokatami i depozytami) oraz transakcją FX spot.
Ćwiczenie 5.5 (Transakcja par FX forward)
W transakcji par FX forward strony kontraktu dokonują w określonych
umową chwilach czasu ![]() wymian kwot
wymian kwot ![]() ,
,
![]() w walucie
w walucie ![]() na kwoty w
walucie
na kwoty w
walucie ![]() po jednym wspólnym kursie
po jednym wspólnym kursie ![]() . Wyprowadź wzór
na kurs
. Wyprowadź wzór
na kurs ![]() przy którym w chwili zawarcia kontraktu jego wartość
wynosi zero.
przy którym w chwili zawarcia kontraktu jego wartość
wynosi zero.
Ćwiczenie 5.6 (Skracanie (rollback) / wydłużanie (rollover) zawartej transakcji FX forward)
Rozpatrzmy ,,żyjącą” transakcję FX forward, która została zawarta z
ceną ![]() i która zapadnie w chwili
i która zapadnie w chwili ![]() . W trakcie trwania tego
kontraktu w chwili bieżącej klient banku, który jest stroną tej
transakcji, prosi o skrócenie (wydłużenie) kontraktu. To skrócenie
(wydłużenie) kontraktu polega na
. W trakcie trwania tego
kontraktu w chwili bieżącej klient banku, który jest stroną tej
transakcji, prosi o skrócenie (wydłużenie) kontraktu. To skrócenie
(wydłużenie) kontraktu polega na
-
anulowaniu oryginalnej transakcji, która miała zapaść w
 ,
, -
zawarciu nowej transakcji FX forward (lub w szczególnym przypadku FX spot) z nowym, wcześniejszym (późniejszym) niż
 , terminem zapadalności
, terminem zapadalności 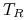 .
.
Wyznacz sprawiedliwą cenę ![]() (kurs) dla ,,zrolowanej” transakcji
FX, którą bank powinien zaproponować klientowi. Oblicz różnicę
(kurs) dla ,,zrolowanej” transakcji
FX, którą bank powinien zaproponować klientowi. Oblicz różnicę
![]() , gdzie
, gdzie ![]() jest bieżącym kursem terminowym na chwilę
jest bieżącym kursem terminowym na chwilę ![]() .
Jaki sens ekonomiczny ma ta różnica?
.
Jaki sens ekonomiczny ma ta różnica?




