Zagadnienia
9. Model Blacka-Scholesa
Od tego rozdziału zajmiemy się badaniem rynku z czasem ciągłym. Zaczniemy od opisu procesu cen, a następnie zdefiniujemy model Blacka-Scholesa.
9.1. Aksjomaty procesu cen
W 1900 roku L. Bachelier zaproponował, żeby dynamikę ceny akcji na
giełdzie paryskiej modelować za pomocą procesów otrzymanych
z przejść granicznych błądzeń losowych, a więc zaproponował
modelowanie ceny ciągłymi procesami ![]() o przyrostach
niezależnych, takimi że przy zmianie czasu o
o przyrostach
niezależnych, takimi że przy zmianie czasu o ![]() zmiana ceny
zmiana ceny
![]() zachowuje się jak
zachowuje się jak ![]() dla małych
przyrostów
dla małych
przyrostów ![]() . We współczesnym języku matematyki jego
postulaty oznaczają, że proces cen powinien mieć postać:
. We współczesnym języku matematyki jego
postulaty oznaczają, że proces cen powinien mieć postać:
gdzie ![]() jest procesem Wienera,
jest procesem Wienera, ![]() ,
, ![]() .
Zatem
.
Zatem ![]() ma rozkład normalny ze średnią
ma rozkład normalny ze średnią ![]() i wariancją
i wariancją
![]() , co będziemy oznaczać
, co będziemy oznaczać ![]() Stąd wynika, że cena akcji może przyjmować ujemne
wartości z dodatnim prawdopodobieństwem. W związku z tym wiele osób
odrzuca ten sposób modelowania ceny (zauważmy jednak, że z reguły
trzech sigm wynika, że dla małych
Stąd wynika, że cena akcji może przyjmować ujemne
wartości z dodatnim prawdopodobieństwem. W związku z tym wiele osób
odrzuca ten sposób modelowania ceny (zauważmy jednak, że z reguły
trzech sigm wynika, że dla małych ![]() szanse na ujemną cenę są
znikome, bo
szanse na ujemną cenę są
znikome, bo ![]() , a ponadto często w statystyce używa
się rozkładu normalnego do modelowania wielkości z istoty rzeczy
nieujemnych np. długości, co nie wzbudza wątpliwości). Inną
konsekwencją przyjęcia modelu Bacheliera jest fakt, że rozkład
przyrostu ceny na ustalonym przedziale czasowym jest taki sam,
niezależnie od ceny początkowej. Dlatego szansa, że cena akcji
sprzedawanej po 50 jednostek spadnie w tym okresie do 45 (strata
w wysokości 10% wartości) jest taka sama, jak szansa, że akcja
w ustalonym okresie czasu warta 10 spadnie do 5 (strata w wysokości
50% wartości). Praca Bacheliera była zbyt nowatorska jak na
ówczesne czasy i bardzo szybko została zapomniana. Odkryto ją
ponownie dopiero w latach siedemdziesiątych dwudziestego wieku.
, a ponadto często w statystyce używa
się rozkładu normalnego do modelowania wielkości z istoty rzeczy
nieujemnych np. długości, co nie wzbudza wątpliwości). Inną
konsekwencją przyjęcia modelu Bacheliera jest fakt, że rozkład
przyrostu ceny na ustalonym przedziale czasowym jest taki sam,
niezależnie od ceny początkowej. Dlatego szansa, że cena akcji
sprzedawanej po 50 jednostek spadnie w tym okresie do 45 (strata
w wysokości 10% wartości) jest taka sama, jak szansa, że akcja
w ustalonym okresie czasu warta 10 spadnie do 5 (strata w wysokości
50% wartości). Praca Bacheliera była zbyt nowatorska jak na
ówczesne czasy i bardzo szybko została zapomniana. Odkryto ją
ponownie dopiero w latach siedemdziesiątych dwudziestego wieku.
W 1965 r. Samuelson zaproponował postulaty, które powinien spełniać
proces cen ![]() :
:
-
Ceny są dodatnie, czyli
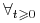
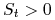 ,
, 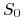 jest
stałą.
jest
stałą. -
Procentowa zmiana cen akcji nie zależy od ceny obecnej ani od cen w przeszłości, czyli
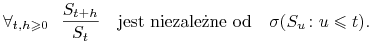
-
Zmiana ta (a dokładniej rozkład zmiany) zależy tylko od długości odcinka czasu, na którym jest rozpatrywana, natomiast nie jest istotne, od którego momentu ją liczymy, tj.
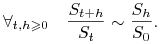
-
Proces
 ma ciągłe trajektorie.
ma ciągłe trajektorie.
Przy założeniach 1–4 można udowodnić, że proces cen wyraża się
przez tzw. geometryczny proces Wienera (gdyż z postulatów wynika, że
![]() jest procesem stacjonarnym o przyrostach niezależnych i o
ciągłych trajektoriach)
jest procesem stacjonarnym o przyrostach niezależnych i o
ciągłych trajektoriach)
| (9.1) |
Pozostaje problem doboru stałych ![]() by wzór (9.1)
miał sens ekonomiczny. Okazuje się, że należy wziąć
by wzór (9.1)
miał sens ekonomiczny. Okazuje się, że należy wziąć ![]() i
i ![]() dla pewnego
dla pewnego ![]() .
Wtedy
.
Wtedy
| (9.2) |
Zatem ![]() ma rozkład lognormalny, tj.
ma rozkład lognormalny, tj.
| (9.3) |
Znajdziemy teraz ekonomiczny sens stałych ![]() ,
, ![]() . Gdy
. Gdy ![]() jest wartością jakiegoś portfela w chwili
jest wartością jakiegoś portfela w chwili ![]() , to dla
, to dla ![]()
jest oczekiwaną stopą zwrotu na jednostkę czasu z tego portfela
w czasie od ![]() do
do ![]() . Wariancja stopy zwrotu na jednostkę czasu
wyraża się wzorem
. Wariancja stopy zwrotu na jednostkę czasu
wyraża się wzorem
Gdy portfel składa się z jednej akcji, to oczywiście ![]() .
Jeśli proces
.
Jeśli proces ![]() jest geometrycznym procesem Wienera, tj.
jest geometrycznym procesem Wienera, tj. ![]() spełnia (9.2), to łatwo udowodnić, że
spełnia (9.2), to łatwo udowodnić, że
Stąd ![]() , odzwierciedlające stałe tendencje zmian cen akcji,
nazywa się współczynnikiem wzrostu (stopą aprecjacji) cen akcji,
a
, odzwierciedlające stałe tendencje zmian cen akcji,
nazywa się współczynnikiem wzrostu (stopą aprecjacji) cen akcji,
a ![]() mierzące zmienność nazywa się współczynnikiem zmienności
cen akcji (dowód tych faktów pozostawiamy jako zadanie — zad.
9.3). W praktyce wielkość
mierzące zmienność nazywa się współczynnikiem zmienności
cen akcji (dowód tych faktów pozostawiamy jako zadanie — zad.
9.3). W praktyce wielkość ![]() podaje się w
procentach.
podaje się w
procentach.
9.2. Klasyczny model Blacka-Scholesa
Teraz opiszemy klasyczny model Blacka-Scholesa
(Blacka-Mertona-Scholesa) z horyzontem ![]() . Niech
. Niech ![]() będzie przestrzenią probabilistyczną z filtracją
będzie przestrzenią probabilistyczną z filtracją ![]() , na której mamy zadany
proces Wienera
, na której mamy zadany
proces Wienera ![]() . Zakładamy, że mamy do czynienia z rynkiem
idealnym, na którym mamy jeden papier ryzykowny, akcje nie płacące
dywidend, o cenie zadanej wzorem
. Zakładamy, że mamy do czynienia z rynkiem
idealnym, na którym mamy jeden papier ryzykowny, akcje nie płacące
dywidend, o cenie zadanej wzorem
| (9.4) |
W §9.1 uzasadniliśmy taki wybór procesu cen. Na tym
rynku mamy także rachunek bankowy o stałej stopie procentowej ![]() w całym okresie handlu
w całym okresie handlu ![]() i ciągłej kapitalizacji, tj.
proces wartości jednostki pieniężnej jest zadany równaniem
i ciągłej kapitalizacji, tj.
proces wartości jednostki pieniężnej jest zadany równaniem
zatem ![]() . Rynek jest idealny, wszyscy mają taką samą
wiedzę, a że informacje w naszym modelu są otrzymywane wyłącznie
z obserwacji procesu cen
. Rynek jest idealny, wszyscy mają taką samą
wiedzę, a że informacje w naszym modelu są otrzymywane wyłącznie
z obserwacji procesu cen ![]() to o
to o ![]() -ciele
-ciele ![]() interpretowanym jako wiedza uzyskana do chwili
interpretowanym jako wiedza uzyskana do chwili ![]() zakładamy, że
zakładamy, że
![]() . Ponieważ jedynym rozwiązaniem
(9.4) jest
. Ponieważ jedynym rozwiązaniem
(9.4) jest
| (9.5) |
więc ![]() . Podsumowując
zakładamy, że filtracja
. Podsumowując
zakładamy, że filtracja ![]() jest uzupełnioną filtracją
procesu Wienera, tj.
jest uzupełnioną filtracją
procesu Wienera, tj. ![]() i
i ![]() .
.
Ten model jest znacznym uproszczeniem rzeczywistości. Jego zaletą są proste założenia zrozumiałe dla wszystkich. Stąd służy on jako pierwsze przybliżenie. Wzory (np. na ceny opcji) i reguły otrzymane dla tego modelu są używane w praktyce w bardziej wyrafinowany sposób.
Konstrukcję modelu rynku zaczynamy od definicji strategii.
Definicja 9.1
Strategią nazywamy proces mierzalny adaptowany
![]() spełniający warunki
spełniający warunki
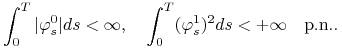 |
(9.6) |
Jak zawsze ![]() interpretujemy jako liczbę jednostek bankowych,
a
interpretujemy jako liczbę jednostek bankowych,
a ![]() jako liczbę akcji. Strategia
jako liczbę akcji. Strategia ![]() jest
jest
![]() adaptowana tzn. dla każdego
adaptowana tzn. dla każdego ![]() wektor losowy
wektor losowy
![]() jest
jest ![]() mierzalny, zatem strategię tworzymy na
podstawie wiedzy dostępnej do chwili
mierzalny, zatem strategię tworzymy na
podstawie wiedzy dostępnej do chwili ![]() .
Proces wartości
portfela (strategii) też definiujemy
jak zwykle, tj.
.
Proces wartości
portfela (strategii) też definiujemy
jak zwykle, tj.
Proces zysków kapitałowych zadany jest przez odpowiednik (3.2):
Warto zauważyć, że z postaci równania zadającego proces cen wynika, że
Warunek (9.6) oraz fakt, że cena ![]() jest procesem
ciągłym zapewniają istnienie całek występujących w definicji
procesu zysku.
jest procesem
ciągłym zapewniają istnienie całek występujących w definicji
procesu zysku.
Definicja 9.2
Mówimy, że strategia ![]() jest samofinansująca się, gdy
zachodzi
jest samofinansująca się, gdy
zachodzi
| (9.7) |
Warunek (9.7) jest równoważny warunkowi:
czyli
Intuicyjnie, portfel ![]() jest samofinansujący się, gdy nie ma
dopływu kapitału z zewnątrz — zmiany wartości portfela wynikają
tylko z naszej polityki, czyli z postaci portfela
jest samofinansujący się, gdy nie ma
dopływu kapitału z zewnątrz — zmiany wartości portfela wynikają
tylko z naszej polityki, czyli z postaci portfela ![]() i ze
zmian cen
i ze
zmian cen ![]() . Warunek (9.7) jest ciągłym odpowiednikiem
warunku (3.5). Klasa wszystkich strategii samofinansujących
się jest przestrzenią liniową. Będziemy ją oznaczać przez
. Warunek (9.7) jest ciągłym odpowiednikiem
warunku (3.5). Klasa wszystkich strategii samofinansujących
się jest przestrzenią liniową. Będziemy ją oznaczać przez ![]() .
.
Przykład 9.1
Strategia ,,kup i trzymaj
aktywo” (buy-and-hold), czyli ![]() ,
,
![]() jest strategią samofinansującą się, bo
jest strategią samofinansującą się, bo
a stąd
Ćwiczenie 9.1
Udowodnić, że strategia ![]() ,
,
![]() ma portfel bogactwa równy
ma portfel bogactwa równy ![]() (a więc taki sam jak strategia ,,kup i trzymaj”), ale
nie jest strategią samofinansującą się.
(a więc taki sam jak strategia ,,kup i trzymaj”), ale
nie jest strategią samofinansującą się.
Definicja arbitrażu i jego sens jest analogiczny jak dla rynku skończonego.
Definicja 9.3
Możliwością arbitrażu ![]() arbitrażem
arbitrażem![]() nazywamy strategię
nazywamy strategię
![]() taką, że
taką, że
| (9.9) |
dla pewnego ![]() .
.
Ponieważ zbiory miary zero pozostają te same dla każdego ![]() , więc jeśli (9.9) zachodzi dla pewnego
, więc jeśli (9.9) zachodzi dla pewnego ![]() , to zachodzi dla każdego
, to zachodzi dla każdego ![]() . Arbitraż
jest sposobem postępowania, który nigdy nie przyniesie straty i daje
możliwość osiągnięcia zysku w sprzyjających okolicznościach. Gdy na
rynku istnieje możliwość arbitrażu, to odpowiednio postępując można
osiągać na nim zysk bez ryzyka. Istnienie arbitrażu świadczy o braku
równowagi na rynku. Na istniejących rynkach finansowych działają
arbitrażyści i nie ma możliwości arbitrażu. Zatem modele opisujące
rzeczywistość powinny być wolne od arbitrażu.
. Arbitraż
jest sposobem postępowania, który nigdy nie przyniesie straty i daje
możliwość osiągnięcia zysku w sprzyjających okolicznościach. Gdy na
rynku istnieje możliwość arbitrażu, to odpowiednio postępując można
osiągać na nim zysk bez ryzyka. Istnienie arbitrażu świadczy o braku
równowagi na rynku. Na istniejących rynkach finansowych działają
arbitrażyści i nie ma możliwości arbitrażu. Zatem modele opisujące
rzeczywistość powinny być wolne od arbitrażu.
Zajmiemy się teraz pojęciem wypłaty.
Definicja 9.4
Wypłatą
europejską ![]() aktywem pochodnym lub kontraktem europejskim
aktywem pochodnym lub kontraktem europejskim![]() z momentem wykonania
z momentem wykonania ![]() nazywamy
zmienną losową
nazywamy
zmienną losową ![]() .
.
Wypłatę ![]() otrzymuje kupujący w chwili
otrzymuje kupujący w chwili ![]() jest to zmienna losowa,
więc jest ona
jest to zmienna losowa,
więc jest ona ![]() -mierzalna, czyli jest skonstruowana
w oparciu o dostępną wiedzę do chwili
-mierzalna, czyli jest skonstruowana
w oparciu o dostępną wiedzę do chwili ![]() , a zatem jej wartość
zależy od procesu cen. Jak zawsze, pojawia się pytanie: jeśli
w momencie
, a zatem jej wartość
zależy od procesu cen. Jak zawsze, pojawia się pytanie: jeśli
w momencie ![]() kupujący otrzymuje
kupujący otrzymuje ![]() , to ile powinien zapłacić za
to teraz? By na nie odpowiedzieć, wprowadzamy, jak dla rynków
skończonych, pojęcie strategii replikującej. Mówimy, że
, to ile powinien zapłacić za
to teraz? By na nie odpowiedzieć, wprowadzamy, jak dla rynków
skończonych, pojęcie strategii replikującej. Mówimy, że
![]() jest strategią replikującą wypłatę
jest strategią replikującą wypłatę ![]() w chwili
w chwili ![]() gdy
gdy ![]() (strategia
(strategia ![]() jest zabezpieczeniem
wypłaty
jest zabezpieczeniem
wypłaty ![]() ). Jeśli wypłata
). Jeśli wypłata ![]() ma choć jedną strategię
replikującą, to mówimy, że
ma choć jedną strategię
replikującą, to mówimy, że ![]() jest osiągalna. Analogicznie jak dla
rynku skończonego wprowadzamy pojęcie bogactwa wypłaty osiągalnej
(tzn. pojęcie jednoznacznej replikowalności), a mianowicie mówimy,
że istnieje proces bogactwa osiągalnej wypłaty
jest osiągalna. Analogicznie jak dla
rynku skończonego wprowadzamy pojęcie bogactwa wypłaty osiągalnej
(tzn. pojęcie jednoznacznej replikowalności), a mianowicie mówimy,
że istnieje proces bogactwa osiągalnej wypłaty ![]() , gdy dla każdych
strategii
, gdy dla każdych
strategii ![]() , takich, że
, takich, że ![]() procesy
procesy ![]() i
i ![]() są nieodróżnialne
(tzn.
są nieodróżnialne
(tzn. ![]() ).
).
Definicja 9.5
Niech ![]() . Na rynku
. Na rynku ![]() bez możliwości arbitrażu ceną arbitrażową
bez możliwości arbitrażu ceną arbitrażową ![]() w chwili
w chwili ![]() osiągalnej wypłaty europejskiej
osiągalnej wypłaty europejskiej ![]() dla której istnieje proces
bogactwa nazywamy wartość w chwili
dla której istnieje proces
bogactwa nazywamy wartość w chwili ![]() strategii samofinansującej
się replikującej wypłatę tzn.
strategii samofinansującej
się replikującej wypłatę tzn. ![]()
Uwaga 9.1
Wybór klasy strategii ![]() jest istotny. Nie
można wziąć, jak dla rynku skończonego,
jest istotny. Nie
można wziąć, jak dla rynku skończonego, ![]() , gdyż
prowadzi to do arbitrażu. Zatem musimy dokonać sensownego wyboru
jakiejś podklasy
, gdyż
prowadzi to do arbitrażu. Zatem musimy dokonać sensownego wyboru
jakiejś podklasy ![]() strategii samofinansujących się
strategii samofinansujących się ![]() .
Wyborem podklasy
.
Wyborem podklasy ![]() zajmiemy się pózniej.
zajmiemy się pózniej.
Taka definicja ceny jest uzasadniona faktem, że dla inwestora jest obojętne, czy ma w swym portfelu instrument finansowy, czy wartość początkową strategii generującej go, gdyż w obu przypadkach otrzymuje na końcu okresu inwestycji tę samą wypłatę (w drugim przypadku musi postępować tak, jak wskazuje strategia replikująca). Można udowodnić wprost, że definicja ceny jest poprawna tzn. że dla każdej wypłaty osiągalnej istnieje proces bogactwa. My to udowodnimy korzystając z idei miary martyngałowej. Wszystkie ceny będziemy dyskontować przez wartość jednostki bankowej, tj.
Definicja 9.6
Miarę
probabilistyczną ![]() na
na ![]() nazywamy miarą
martyngałową, gdy
nazywamy miarą
martyngałową, gdy ![]() i
i ![]() jest
jest ![]() -martyngałem
lokalnym.
-martyngałem
lokalnym.
Zaczniemy od twierdzenia podającego postać miary martyngałowej dla
zdyskontowanego procesu cen ![]() .
.
Twierdzenie 9.1
Miara probabilistyczna ![]() o gęstości
o gęstości
| (9.10) |
jest jedyną miarą martyngałową. Ponadto proces ![]() jest
jest
![]() -martyngałem o dynamice
-martyngałem o dynamice
| (9.11) |
gdzie ![]() jest procesem
Wienera względem
jest procesem
Wienera względem ![]() i filtracji
i filtracji ![]() .
.
Ponieważ ![]() , więc ze wzoru na całkowanie
przez części
, więc ze wzoru na całkowanie
przez części
| (9.12) |
Zatem, korzystając z dynamiki ![]() tzn. (9.4), otrzymujemy
tzn. (9.4), otrzymujemy
Chcemy, by ![]() dla procesu
Wienera
dla procesu
Wienera ![]() przy pewnej mierze
przy pewnej mierze ![]() . Zatem powinno
zachodzić
. Zatem powinno
zachodzić
| (9.13) |
Na mocy tw. Girsanowa miara ![]() zadana wzorem (9.10)
jest dobrze zdefiniowaną miarą probabilistyczną i
zadana wzorem (9.10)
jest dobrze zdefiniowaną miarą probabilistyczną i ![]() jest procesem Wienera względem
jest procesem Wienera względem ![]() .
Wtedy zachodzi (9.13), czyli zachodzi (9.11).
Proces
.
Wtedy zachodzi (9.13), czyli zachodzi (9.11).
Proces ![]() , przy mierze
, przy mierze ![]() jest równy całce
stochastycznej względem procesu Wienera plus stała, więc jest
jest równy całce
stochastycznej względem procesu Wienera plus stała, więc jest
![]() -martyngałem lokalnym, czyli
-martyngałem lokalnym, czyli ![]() jest miarą martyngałową dla
jest miarą martyngałową dla
![]() . Jedyność
. Jedyność ![]() pozostawiamy jako zadanie dla Czytelnika (zad.
9.10). Ponieważ
pozostawiamy jako zadanie dla Czytelnika (zad.
9.10). Ponieważ
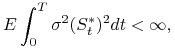 |
(9.14) |
to ![]() jest
jest ![]() -martyngałem.
-martyngałem.
Uwaga 9.2
a) Warunek (9.11) można zapisać równoważnie
| (9.15) |
gdyż z (9.13) mamy
Zatem przy zamianie miary na równoważną miarę martyngałową współczynnik zmienności ceny akcji nie ulega zmianie.
b) Z (9.15) wynika, że przy mierze martyngałowej ![]() proces cen ma postać
proces cen ma postać
| (9.16) |
Analogicznie jak w przypadku rynku skończonego istnieje ważna charakteryzacja portfeli samofinansujących się w terminach procesu zdyskontowanych cen:
Twierdzenie 9.2
Strategia ![]() jest
strategią samofinansującą się wtedy i tylko wtedy, gdy zachodzi
jest
strategią samofinansującą się wtedy i tylko wtedy, gdy zachodzi
| (9.17) |
![]() Konieczność. Ponieważ
Konieczność. Ponieważ
| (9.18) |
więc kolejno ze wzoru na całkowanie przez części, definicji strategii samofinansującej się i (9.12) mamy
Zatem równość (9.17) jest spełniona.
Dostateczność. Z (9.18) mamy
| (9.19) |
Ze wzoru (9.12) otrzymujemy
| (9.20) |
Z założenia (9.17) wynika, że lewe strony wzorów (9.19) i (9.20) są równe, więc i prawe są równe, zatem
czyli ![]() .
.
Lemat ten wykorzystuje się do znajdowania strategii samofinansujących się replikujących daną wypłatę. Z niego wynika także:
Twierdzenie 9.3
Miara ![]() jest miarą martyngałową dla
jest miarą martyngałową dla ![]() wtedy i tylko wtedy,
gdy dla każdej strategii samofinansującej się
wtedy i tylko wtedy,
gdy dla każdej strategii samofinansującej się ![]() zdyskontowany proces bogactwa
zdyskontowany proces bogactwa ![]() jest
jest ![]() -martyngałem
lokalnym.
-martyngałem
lokalnym.
Konieczność. Korzystając z (9.11) i (9.17) mamy
a ponieważ ![]() jest
jest ![]() procesem Wienera, to
procesem Wienera, to
![]() jest
jest ![]() -martyngałem lokalnym.
-martyngałem lokalnym.
Dostateczność. Biorąc strategię stałą ![]() otrzymujemy, że
otrzymujemy, że ![]() i
i
![]() .
. ![]() jest
jest ![]() -martyngałem
lokalnym z założenia, czyli
-martyngałem
lokalnym z założenia, czyli ![]() jest
jest ![]() -martyngałem lokalnym.
-martyngałem lokalnym.
Rozpatrywanie rynku ze wszystkimi możliwymi strategiami samofinansującymi się prowadzi do arbitrażu. Zatem, by wykluczyć arbitraż, ograniczamy klasę strategii do strategii dopuszczalnych
Definicja 9.7
Niech ![]() będzie miarą martyngałową dla
będzie miarą martyngałową dla ![]() .
Strategię
.
Strategię ![]() nazywamy dopuszczalną
(
nazywamy dopuszczalną
(![]() –dopuszczalną), gdy proces
–dopuszczalną), gdy proces
jest ![]() -martyngałem.
-martyngałem.
Ponieważ dla ![]() istnieje dokładnie jedna miara martyngałowa, to
mówimy, że
istnieje dokładnie jedna miara martyngałowa, to
mówimy, że ![]() jest dopuszczalna (zamiast
jest dopuszczalna (zamiast
![]() –dopuszczalna), gdyż nie ma wątpliwości o jaką miarę
martyngałową chodzi.
Zbiór takich strategii będziemy oznaczać przez
–dopuszczalna), gdyż nie ma wątpliwości o jaką miarę
martyngałową chodzi.
Zbiór takich strategii będziemy oznaczać przez ![]() .
.
Udowodnimy teraz, że wzięcie ![]() jest dobrym wyborem
klasy portfeli.
jest dobrym wyborem
klasy portfeli.
Twierdzenie 9.4
Rynek
![]() jest wolny od arbitrażu.
jest wolny od arbitrażu.
Weźmy ![]() takie, że
takie, że ![]() i
i ![]() . Udowodnimy, że
. Udowodnimy, że ![]() ,
więc
,
więc ![]() nie jest arbitrażem, a zatem na rynku
nie jest arbitrażem, a zatem na rynku ![]() nie istnieje arbitraż.
nie istnieje arbitraż.
Z założenia ![]() jest
jest ![]() -martyngałem, wobec tego
-martyngałem, wobec tego
| (9.21) |
Ponieważ ![]() (bo
(bo ![]() ),
), ![]() ,
więc (9.21) implikuje
,
więc (9.21) implikuje ![]() , a stąd
z równoważności miar
, a stąd
z równoważności miar ![]() i
i ![]() otrzymujemy
otrzymujemy
![]() .
.
Definicja 9.8
Trójkę ![]() nazywamy klasycznym modelem
Blacka-Scholesa rynku finansowego (w skrócie modelem
Blacka-Scholesa; niektórzy autorzy używaja nazwy model
Blacka-Mertona-Scholesa).
nazywamy klasycznym modelem
Blacka-Scholesa rynku finansowego (w skrócie modelem
Blacka-Scholesa; niektórzy autorzy używaja nazwy model
Blacka-Mertona-Scholesa).
9.3. Rynkowa cena ryzyka.
Załóżmy, że na rynku Blacka-Scholesa bez
możliwości arbitrażu mamy dodatkowy instrument pierwotny, zatem mamy
dwa instrumenty pierwotne, którymi możemy handlować i których ceny
zadane są względem jednowymiarowego procesu Wienera ![]() (tego
samego) równaniami
(tego
samego) równaniami
czyli na tym rynku mamy jedno źródło losowości — proces Wienera
![]() i rynek rozszerzony jest rynkiem bez możliwości arbitrażu. Gdy
i rynek rozszerzony jest rynkiem bez możliwości arbitrażu. Gdy
![]() jest miarą martyngałową dla rynku Blacka-Scholesa
jest miarą martyngałową dla rynku Blacka-Scholesa ![]() , to
, to
jest ![]() -procesem Wienera. Ponadto
-procesem Wienera. Ponadto
a ponieważ proces ![]() jest
jest ![]() -martyngałem, więc
-martyngałem, więc
Stąd
Gdy proces ceny ![]() jest zadany wzorem (9.2), to wielkość
jest zadany wzorem (9.2), to wielkość
ekonomiści nazywają rynkową ceną ryzyka (przez analogię do modelu CAPM) — jest to nadwyżka średniego zwrotu z akcji ponad zwrot z instrumentu bez ryzyka mierzona w jednostkach ryzyka. Wykazaliśmy, że instrumenty bazowe, którymi można handlować na rozszerzonym rynku Blacka-Scholesa bez możliwości arbitrażu z instrumentami bazowymi o cenach zadanych wzorem (9.2) (z różnymi parametrami) mają tę samą rynkową cenę ryzyka. Warto zauważyć, że ta terminologia została tu użyta w innym sensie niż dotąd: nie jest to cena arbitrażowa jakiegoś jednego instrumentu, którym możemy handlować na rynku.
Ponieważ ![]() , więc
, więc ![]() wyznacza
gęstość miary martyngałowej
wyznacza
gęstość miary martyngałowej ![]() względem
względem ![]()
i stąd miara ![]() jest nazywana miarą neutralną względem ryzyka.
jest nazywana miarą neutralną względem ryzyka.
9.4. Zagadnienia i zadania na ćwiczenia
Skorzystać z faktu, że gdy ![]() ,
,
![]() , to
, to ![]() ,
, ![]()
więc korzystając z faktu podanego we wskazówce znajdujemy wartość oczekiwaną i wariancję tego ułamka. Reszta jest prostym przejściem do granicy.
Ćwiczenie 9.4
Pokazać, że średnia wartość ceny rośnie ze stopą równą ![]() , czyli
, czyli
![]() . Stąd wynika, że gdy średnia stopa zwrotu
z akcji ma być taka sama jak dla papierów bez ryzyka, to
. Stąd wynika, że gdy średnia stopa zwrotu
z akcji ma być taka sama jak dla papierów bez ryzyka, to ![]() .
.
Skorzystać ze wskazówki do poprzedniego zadania.
Ćwiczenie 9.5
Rozważmy na rynku Blacka-Scholesa akcję z ceną początkową 40, oczekiwanym zwrotem 16% p.a., współczynnikiem zmienności 20% p.a. (na rynku te wielkości podaje się w procentach). Znaleźć:
a) 95% przedział ufności dla ceny akcji za trzy miesiące.
b) średnią cenę akcji za trzy miesiące.
Stosujemy wzór Itô do funkcji ![]() i procesu
i procesu ![]() zadanego stochastycznym równaniem różniczkowym
zadanego stochastycznym równaniem różniczkowym
(wtedy ![]()
Ćwiczenie 9.7
Udowodnić, że portfel stały jest strategią samofinansującą się.
Portfel stały jest kombinacją liniową strategii ,,kup i trzymaj” oraz włóż pieniądze do banku, które są strategiami samofinansującymi się (przykład 9.1), a więc portfel stały jest strategią samofinansującą się.
Ćwiczenie 9.8
Analogicznie jak w czasie dyskretnym, znając strategię inwestowania
w papiery ryzykowne i kapitał początkowy, znamy całą strategię
samofinansującą się. Formalnie: udowodnić, że dla każdego ![]() i procesu prognozowalnego
i procesu prognozowalnego ![]() takiego, że
całka
takiego, że
całka ![]() istnieje, przyjęcie
istnieje, przyjęcie
definiuje jednoznacznie portfel samofinansujący się
![]() , taki, że
, taki, że ![]() .
.
Ćwiczenie 9.9
Udowodnić, że jeśli rynek ![]() dla
dla ![]() jest wolny
od arbitrażu, to rynek
jest wolny
od arbitrażu, to rynek ![]() dla
dla ![]() , gdzie
, gdzie ![]() , jest wolny od arbitrażu.
, jest wolny od arbitrażu.
Jeśli istnieje arbitraż ![]() dla
dla ![]() , to
inwestując w chwili
, to
inwestując w chwili ![]() całe bogactwo
całe bogactwo ![]() w aktywa bez ryzyka otrzymujemy strategię arbitrażową dla rynku
z czasem
w aktywa bez ryzyka otrzymujemy strategię arbitrażową dla rynku
z czasem ![]() .
.
Ćwiczenie 9.10
Udowodnić, że dla klasycznego rynku Blacka-Scholesa istnieje dokładnie jedna miara martyngałowa.
Ćwiczenie 9.11
Udowodnić, że na rynku Blacka-Scholesa strategia ,,kup i trzymaj aktywo” (patrz przykł. 9.1) jest strategią dopuszczalną.
![]() , więc
, więc ![]() jest
jest
![]() martyngałem.
martyngałem.




