Zagadnienia
10. Doświadczenia Mendla: łańcuchy Markowa w klasycznej genetyce II
10.1. Łańcuchy pochłaniające i ciągłe krzyżowanie z dominantą
Dla łańcuchów pochłaniających postać kanoniczna macierzy przejścia przedstawia się następująco
gdzie ![]() oznacza macierz jednostkową wymiaru
oznacza macierz jednostkową wymiaru ![]() reprezentującą
reprezentującą ![]() stanów pochłaniających,
stanów pochłaniających, ![]() jest macierzą wymiaru
jest macierzą wymiaru ![]() przejścia ze stanów nieistotnych do stanów pochłaniających, a
przejścia ze stanów nieistotnych do stanów pochłaniających, a ![]() — macierzą
— macierzą ![]() przejścia ze stanów nieistotnych do stanów nieistotnych. Zauważmy, że dla takich łańcuchów wygodniej jest zdefiniować postać kanoniczną inaczej niż poprzednio — zaczynamy numerowanie od stanów pochłaniających, dopiero później bierzemy pod uwagę stany nieistotne.
przejścia ze stanów nieistotnych do stanów nieistotnych. Zauważmy, że dla takich łańcuchów wygodniej jest zdefiniować postać kanoniczną inaczej niż poprzednio — zaczynamy numerowanie od stanów pochłaniających, dopiero później bierzemy pod uwagę stany nieistotne.
Z własności stanów nieistotnych i stanów pochłaniających wynika, że
-
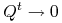 dla
dla 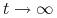 (zbieżność po wyrazach);
(zbieżność po wyrazach); -
macierz
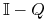 jest odwracalna;
jest odwracalna; -
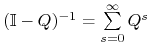 .
.
Własność 1. wynika z ogólnego twierdzenia dotyczącego łańcuchów Markowa, które orzeka, że niezależnie od stanu początkowego prawdopodobieństwo trafienia do stanu komunikującego się po ![]() krokach dąży do
krokach dąży do ![]() przy
przy ![]() , a ponieważ
, a ponieważ ![]() odpowiada stanom nieistotnym, zatem każde z pozostałych prawdopodobieństw dąży do
odpowiada stanom nieistotnym, zatem każde z pozostałych prawdopodobieństw dąży do ![]() . Dalej zauważmy, że
. Dalej zauważmy, że
Skoro ![]() , to
, to ![]() , a z ciągłości wyznacznika wynika, że dla dostatecznie dużych
, a z ciągłości wyznacznika wynika, że dla dostatecznie dużych ![]() zachodzi
zachodzi ![]() , czyli także
, czyli także ![]() , więc
macierz
, więc
macierz ![]() jest odwracalna. Stąd
jest odwracalna. Stąd
i przechodząc do granicy ![]() dostajemy wzór 3.
dostajemy wzór 3.
W przypadku łańcuchów pochłaniających interesują nas głównie następujące zagadnienia dotyczące łańcucha, dla którego stanem początkowym jest pewien nieistotny stan ![]() .
.
-
[I]
-
Jaka jest oczekiwana liczba przejść przez stan
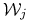 , zakładając że stanem początkowym jest
, zakładając że stanem początkowym jest 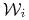 ?
? -
Jaka jest oczekiwana liczba kroków przed absorpcją, jeśli stanem początkowym jest
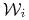 ?
? -
Jakie jest prawdopodobieństwo absorpcji przez dany stan pochłaniający
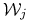 , jeśli stanem początkowym jest
, jeśli stanem początkowym jest 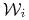 ?
?
Dla macierzy przejścia w postaci kanonicznej definiujemy następującą macierz fundamentalną
łańcucha pochłaniającego. Macierz ta zawiera wszystkie istotne informacje dotyczące zachowań asymptotycznych. W szczególności
Twierdzenie 10.1
Niech ![]() będzie macierzą fundamentalną łańcucha pochłaniającego.
będzie macierzą fundamentalną łańcucha pochłaniającego.
-
Oczekiwana liczba przejść przez stan
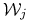 przy stanie początkowym
przy stanie początkowym 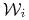 jest równa
jest równa 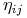 .
. -
Oczekiwana liczba kroków przed absorpcją dla łańcucha o stanie początkowym
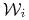 zadana jest jako suma wyrazów w
zadana jest jako suma wyrazów w 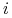 . wierszu macierzy
. wierszu macierzy 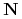 .
. -
Niech
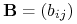 będzie
będzie 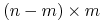 macierzą prawdopodobieństw absorpcji przez stan
macierzą prawdopodobieństw absorpcji przez stan 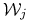 przy stanie początkowym
przy stanie początkowym 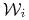 . Wtedy
. Wtedy 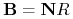 .
.
Niech ![]() oznacza oczekiwaną liczba przejść przez stan
oznacza oczekiwaną liczba przejść przez stan ![]() przy stanie początkowym
przy stanie początkowym ![]() . Wprowadźmy zmienną losową
. Wprowadźmy zmienną losową
Niech ![]() oznacza wartość średnią
oznacza wartość średnią ![]() przy warunku, że proces zaczął się w stanie
przy warunku, że proces zaczął się w stanie ![]() . Wtedy
. Wtedy
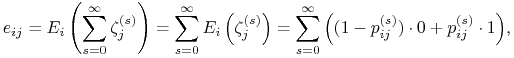 |
czyli ostatecznie ![]() . Skoro
. Skoro ![]() jest
jest ![]() . wyrazem macierzy
. wyrazem macierzy ![]() , to
, to ![]() jest
jest ![]() . wyrazem macierzy
. wyrazem macierzy ![]() , czyli
, czyli ![]() .
.
Bezpośrednio z tego wzoru otrzymujemy także, że średni czas do absorpcji jest sumą wyrazów w wierszu ![]() .
.
Wyprowadzimy teraz wzór rekurencyjny na prawdopodobieństwo ![]() . Niech
. Niech ![]() będzie stanem początkowym nieistotnym. W pierwszym kroku łańcuch może przejść do interesującego nas stanu pochłaniającego
będzie stanem początkowym nieistotnym. W pierwszym kroku łańcuch może przejść do interesującego nas stanu pochłaniającego ![]() , do innego stanu pochłaniającego
, do innego stanu pochłaniającego ![]() ,
, ![]() , albo do któregoś ze stanów nieistotnych
, albo do któregoś ze stanów nieistotnych ![]() z prawdopodobieństwami zadanymi przez macierz
z prawdopodobieństwami zadanymi przez macierz ![]() . Prawdopodobieństwa absorpcji przez stan
. Prawdopodobieństwa absorpcji przez stan ![]() ze stanu
ze stanu ![]() ,
, ![]() oraz
oraz ![]() są odpowiednio równe
są odpowiednio równe
![]() ,
, ![]() oraz
oraz ![]() . Stąd
. Stąd
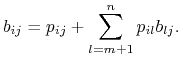 |
Skoro ![]() oraz
oraz ![]() są odpowiednio stanem nieistotnym i pochłaniającym, więc
są odpowiednio stanem nieistotnym i pochłaniającym, więc ![]() jest
jest ![]() . wyrazem macierzy
. wyrazem macierzy ![]() i analogicznie
i analogicznie ![]() jest
jest ![]() . wyrazem macierzy
. wyrazem macierzy ![]() . Zatem
. Zatem
Zastosujemy teraz powyższe twierdzenie do opisu asymptotyki rosyjskiej ruletki oraz do opisu doświadczenia polegającego na ciągłym krzyżowaniu z dominantą.
W przypadku rosyjskiej ruletki mamy jeden stan pochłaniający ![]() i jeden stan nieistotny
i jeden stan nieistotny ![]() . Odpowiednie podmacierze macierzy
. Odpowiednie podmacierze macierzy ![]() są jednoelementowe
są jednoelementowe
Ponieważ jest tylko jeden stan pochłaniający, więc oczywiście prawdopodobieństwo znalezienia się w tym stanie po dostatecznie długim czasie wynosi ![]() , natomiast
oczekiwana liczba kroków do absorpcji równa się
, natomiast
oczekiwana liczba kroków do absorpcji równa się ![]() .
.
Ciągłe krzyżowanie z dominantą
Rozpatrzmy teraz następujący ciąg doświadczeń tworzący
łańcuch Markowa. Bierzemy ustalonego osobnika o genotypie dominującym ![]() i krzyżujemy go z nieznanym osobnikiem. W wyniku eksperymentu dostajemy potomka o genotypie zależnym od genotypu drugiego rodzica z prawdopodobieństwami wynikającymi z prawa Mendla. Mamy zatem
i krzyżujemy go z nieznanym osobnikiem. W wyniku eksperymentu dostajemy potomka o genotypie zależnym od genotypu drugiego rodzica z prawdopodobieństwami wynikającymi z prawa Mendla. Mamy zatem ![]() możliwe wyniki eksperymentu, ponieważ są
możliwe wyniki eksperymentu, ponieważ są ![]() genotypy. Ponumerujmy je w następujący sposób:
genotypy. Ponumerujmy je w następujący sposób:
Odpowiednie prawdopodobieństwa wynoszą
-
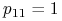 , gdyż zawsze ze skrzyżowania dominanty z dominantą otrzymujemy ten sam genotyp. Stąd
, gdyż zawsze ze skrzyżowania dominanty z dominantą otrzymujemy ten sam genotyp. Stąd 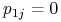 dla
dla 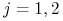 i stan
i stan 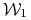 jest pochłaniający.
jest pochłaniający. -
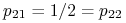 oraz
oraz 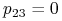 , gdyż krzyżując dominantę z hybrydą otrzymujemy z prawdopodobieństwem
, gdyż krzyżując dominantę z hybrydą otrzymujemy z prawdopodobieństwem 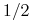 albo dominantę, albo hybrydę, nie możemy natomiast dostać osobnika recesywnego;
albo dominantę, albo hybrydę, nie możemy natomiast dostać osobnika recesywnego;
-
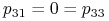 ,
, 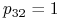 , ponieważ krzyżując osobnika recesywnego z dominantą zawsze dostajemy hybrydę.
, ponieważ krzyżując osobnika recesywnego z dominantą zawsze dostajemy hybrydę.
Dla tego łańcucha Markowa macierz przejścia ma postać
![\mathbf{P}_{D}=\left(\begin{array}[]{ccc}1&0&0\\
0,5&0,5&0\\
0&1&0\end{array}\right),](wyklady/mbm/mi/mi889.png) |
dla której
Policzmy macierz fundamentalną
![\mathbf{N}=(\mathbb{I}-Q)^{{-1}}=\left(\begin{array}[]{cc}0,5&0\\
-1&1\end{array}\right)^{{-1}}=2\left(\begin{array}[]{cc}1&0\\
1&0,5\end{array}\right).](wyklady/mbm/mi/mi849.png) |
Na jej podstawie wnioskujemy, że jeśli wybranym rodzicem była hybryda, to średni czas do absorpcji wynosi ![]() , natomiast jeśli osobnik recesywny, to
, natomiast jeśli osobnik recesywny, to ![]() . Możemy jeszcze sprawdzić punkt
. Możemy jeszcze sprawdzić punkt ![]() . twierdzenia wykonując mnożenie
. twierdzenia wykonując mnożenie
co oczywiście potwierdza, że z prawdopodobieństwem ![]() nasz eksperyment kończy się osobnikami o genotypie
nasz eksperyment kończy się osobnikami o genotypie ![]() .
.
Zauważmy jeszcze, że dokładnie w taki sam sposób możemy opisać ciągłe krzyżowanie z osobnikiem recesywnym. Wtedy macierz przejścia ma postać
![\mathbf{P}_{R}=\left(\begin{array}[]{ccc}1&0&0\\
0,5&0,5&0\\
0&1&0\end{array}\right),](wyklady/mbm/mi/mi890.png) |
gdzie tym razem ![]() ,
, ![]() oraz
oraz ![]() , zatem odpowiednio numerując stany dostajemy dokładnie taką samą dynamikę łańcucha pochłaniającego jak w przypadku krzyżowania z dominantą.
, zatem odpowiednio numerując stany dostajemy dokładnie taką samą dynamikę łańcucha pochłaniającego jak w przypadku krzyżowania z dominantą.
10.2. Łańcuchy regularne i ciągłe krzyżowanie z hybrydą
Zajmiemy się teraz pewnym szczególnym przypadkiem łańcuchów nieprzywiedlnych.
Definicja 10.1
Łańcuch nieprzywiedlny nazwiemy regularnym, jeśli istnieje taka liczba ![]() , że z każdego stanu
, że z każdego stanu ![]() ,
, ![]() można dojść do dowolnego stanu
można dojść do dowolnego stanu ![]() ,
, ![]() w dokładnie
w dokładnie ![]() krokach.
krokach.
Zauważmy, że rzut monetą jest łańcuchem regularnym, dla którego ![]() . Natomiast łatwo podać przykład łańcucha nieprzywiedlnego, który nie jest regularny. Weźmy dla przykładu łańcuch o dwóch stanach
. Natomiast łatwo podać przykład łańcucha nieprzywiedlnego, który nie jest regularny. Weźmy dla przykładu łańcuch o dwóch stanach ![]() ,
, ![]() , dla którego macierz przejścia ma postać
, dla którego macierz przejścia ma postać
zatem np. ze stanu ![]() do
do ![]() przechodzimy zawsze w nieparzystej liczbie kroków, podczas gdy ze stanu
przechodzimy zawsze w nieparzystej liczbie kroków, podczas gdy ze stanu ![]() do niego samego — w parzystej. Tak zdefiniowany łańcuch jest oczywiście łańcuchem okresowym. Co więcej, można udowodnić następujące twierdzenie
do niego samego — w parzystej. Tak zdefiniowany łańcuch jest oczywiście łańcuchem okresowym. Co więcej, można udowodnić następujące twierdzenie
Twierdzenie 10.2
W nieprzywiedlnym łańcuchu Markowa wszystkie stany są tego samego typu, tzn. jeśli choć jeden stan jest powracający, to wszystkie są powracające, jeśli choć jeden jest zerowy, to wszystkie są zerowe, a jeśli choć jeden jest okresowy o okresie ![]() , to wszystkie są okresowe o okresie
, to wszystkie są okresowe o okresie ![]() .
.
Niech ![]() ,
, ![]() będą dwoma różnymi stanami. Ponieważ stany te komunikują się, więc istnieją takie
będą dwoma różnymi stanami. Ponieważ stany te komunikują się, więc istnieją takie ![]() , że
, że
Stosując wzór na prawdopodobieństwo całkowite
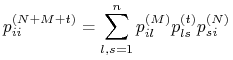 |
dostajemy nierówność
gdzie ![]() ,
, ![]() oraz
oraz ![]() . Postępując analogicznie otrzymujemy nierówność
. Postępując analogicznie otrzymujemy nierówność
Stąd
Powyższe nierówności wykazują, że własności asymptotyczne ciągów ![]() oraz
oraz ![]() są takie same. W szczególności, jeśli stan
są takie same. W szczególności, jeśli stan ![]() jest zerowy,
jest zerowy, ![]() przy
przy ![]() , to także
, to także ![]() jest zerowy. Z kolei jeśli
jest zerowy. Z kolei jeśli ![]() jest powracający, czyli
jest powracający, czyli ![]() , to
, to ![]() ma tę samą własność. Załóżmy teraz, że
ma tę samą własność. Załóżmy teraz, że ![]() jest okresowy o okresie
jest okresowy o okresie ![]() . Ponieważ
. Ponieważ ![]() , więc
, więc ![]() (
(![]() dzieli
dzieli ![]() ). Pokażemy, że
). Pokażemy, że ![]() jest okresowy i jego okres
jest okresowy i jego okres ![]() . Zauważmy, że jeśli dla pewnego
. Zauważmy, że jeśli dla pewnego ![]() zachodzi
zachodzi ![]() , to także
, to także ![]() , zatem
, zatem ![]() , czyli
, czyli ![]() , więc
, więc ![]() . Analogicznie
. Analogicznie ![]() , skąd
, skąd ![]() .
.
W ogólnym przypadku dla łańcuchów nieprzywiedlnych asymptotykę opisuje następujące twierdzenie ergodyczne, którego dowód pomijamy.
Twierdzenie 10.3
Łańcuch Markowa jest nieprzywiedlny wtw jeśli dla każdego ![]() istnieje niezależna od
istnieje niezależna od ![]() granica
granica
przy czym ![]() są jednoznacznym rozwiązaniem układu
są jednoznacznym rozwiązaniem układu
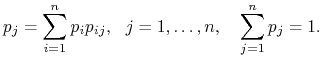 |
Taki asymptotyczny rozkład prawdopodobieństwa nazywamy rozkładem stacjonarnym. Wynika stąd, że zachowanie asymptotyczne badanego łańcucha nie zależy od stanu początkowego — łańcuch ma własność ,,zapominania” rozkładu początkowego.
Dla łańcuchów regularnych można udowodnić twierdzenie silniejsze.
Twierdzenie 10.4
Macierz ![]() łańcucha regularnego ma pojedynczą wartość własną równą
łańcucha regularnego ma pojedynczą wartość własną równą ![]() . Macierz
. Macierz ![]() zbiega do macierzy stochastycznej
zbiega do macierzy stochastycznej ![]() o wyrazach dodatnich, której wszystkie wiersze
o wyrazach dodatnich, której wszystkie wiersze ![]() są jednakowe. Zachodzi
są jednakowe. Zachodzi ![]() .
.
Ponieważ dla łańcucha regularnego wszystkie wyrazy macierzy ![]() są dodatnie, więc twierdzenie to jest bezpośrednim wnioskiem z twierdzenia Frobeniusa – Perrona dla macierzy o wszystkich wyrazach dodatnich.
są dodatnie, więc twierdzenie to jest bezpośrednim wnioskiem z twierdzenia Frobeniusa – Perrona dla macierzy o wszystkich wyrazach dodatnich.
Niech ![]() będzie macierzą przejścia łańcucha regularnego, natomiast
będzie macierzą przejścia łańcucha regularnego, natomiast ![]() jej macierzą graniczną. Można pokazać, że macierz
jej macierzą graniczną. Można pokazać, że macierz
jest odwracalna, co więcej
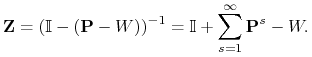 |
Macierz ![]() nazywamy macierzą fundamentalną łańcucha regularnego i dzięki niej możemy wyznaczyć czasy przejścia i powrotów opisane macierzą
nazywamy macierzą fundamentalną łańcucha regularnego i dzięki niej możemy wyznaczyć czasy przejścia i powrotów opisane macierzą ![]() . Mamy
. Mamy
gdzie ![]() jest macierzą o wszystkich wyrazach równych
jest macierzą o wszystkich wyrazach równych ![]() ,
,
![]() to macierz, która ma na przekątnej wyrazy takie same jak
to macierz, która ma na przekątnej wyrazy takie same jak ![]() i zera poza przekątną, natomiast
i zera poza przekątną, natomiast ![]() jest macierzą diagonalną o wyrazach na przekątnej równych
jest macierzą diagonalną o wyrazach na przekątnej równych ![]() , gdzie
, gdzie ![]() oznacza rozkład stacjonarny.
W szczególności wyrazy na przekątnej
oznacza rozkład stacjonarny.
W szczególności wyrazy na przekątnej ![]() zadają średni pierwszy czas powrotu do stanu
zadają średni pierwszy czas powrotu do stanu ![]() .
.
Zastosujmy najpierw powyższe twierdzenia do rzutu monetą.
W tym przypadku rozkład stacjonarny znajdujemy bez trudu, gdyż ![]() dla dowolnego
dla dowolnego ![]() , zatem
, zatem ![]() . Policzymy jeszcze macierz
. Policzymy jeszcze macierz ![]() , choć możemy się spodziewać rezultatu — średnio co drugi rzut powinien dawać
, choć możemy się spodziewać rezultatu — średnio co drugi rzut powinien dawać ![]() i co drugi
i co drugi ![]() , zatem średni czas powrotu szacujemy jako
, zatem średni czas powrotu szacujemy jako ![]() .
.
co oczywiście implikuje, że średni czas powrotu wynosi ![]() rzuty, natomiast średni czas przejścia od
rzuty, natomiast średni czas przejścia od ![]() do
do ![]() i odwrotnie wynosi
i odwrotnie wynosi ![]() .
.
Ciągłe krzyżowanie z hybrydą
W tym paragrafie omówimy doświadczenie genetyczne polegające na ciągłym krzyżowaniu z hybrydą. Przebieg doświadczenia jest analogiczny jak w omówionym już przypadku krzyżowania z dominantą, ale matematyczny opis doświadczenia prowadzi do innego typu łańcucha Markowa. W tym łańcuchu mamy także ![]() możliwe stany
możliwe stany ![]() ,
, ![]() i
i ![]() . Macierz przejścia tego łańcucha ma postać
. Macierz przejścia tego łańcucha ma postać
![\mathbf{P}=\left(\begin{array}[]{ccc}0,5&0,5&0\\
0,25&0,5&0,25\\
0&0,5&0,5\end{array}\right)](wyklady/mbm/mi/mi831.png) |
i łatwo sprawdzimy, że ![]() jest macierzą o wszystkich wyrazach dodatnich. Zatem mamy do czynienia z łańcuchem regularnym. Policzmy jego rozkład stacjonarny
jest macierzą o wszystkich wyrazach dodatnich. Zatem mamy do czynienia z łańcuchem regularnym. Policzmy jego rozkład stacjonarny
skąd dostajemy
Wobec tego przy ciągłym krzyżowaniu z hybrydą dostaniemy następujący wynik eksperymentu: bez względu na genotyp drugiego praprzodka po dostatecznie długim czasie średnio ![]() potomków będzie wykazywało fenotyp dominanty, a
potomków będzie wykazywało fenotyp dominanty, a ![]() fenotyp recesywny. Otrzymaliśmy zatem potwierdzenie pierwotnych wyników uzyskanych przez Mendla przy krzyżowaniu groszku, gdzie średnio było
fenotyp recesywny. Otrzymaliśmy zatem potwierdzenie pierwotnych wyników uzyskanych przez Mendla przy krzyżowaniu groszku, gdzie średnio było ![]() strąków zielonych i
strąków zielonych i ![]() strąków żółtych.
strąków żółtych.




