Zagadnienia
11. Modele z zależnością przestrzenną: dyfuzja w procesach biologicznych
Do tej pory rozważaliśmy modele populacyjne, w których nie uwzględnialiśmy zależności od położenia osobników w przestrzeni, a tylko średnie zagęszczenia i ich zmiany w czasie. Takie podejście do modelowania dynamiki populacji kryje za sobą dodatkowe założenia dotyczące równomiernego rozłożenia przestrzennego osobników danej populacji oraz braku istotnego wpływu zmian położenia na opisywany proces. Oczywiste wydaje się, że w wielu przypadkach położenie i ruch w przestrzeni odgrywają dużą, jeśli nie zasadniczą rolę w przebiegu danego procesu. W związku z tym kolejną część wykładu poświęcimy omówieniu jednego z możliwych sposobów modelowania ruchu, tzw. procesu dyfuzji. W przypadku procesów chemicznych dyfuzja opisuje ruch substancji w kierunku od większych do mniejszych stężeń. Możliwe są oczywiście także przepływy innego typu — np. chemotaksja działa w pewnym sensie przeciwnie do dyfuzji.
Wyprowadzimy najpierw równanie dyfuzji substancji chemicznej w przestrzeni jednowymiarowej (dla przestrzeni dwu i trójwymiarowej rozumowanie przebiega analogicznie). Załóżmy, że mamy bardzo wąską rurkę o długości ![]() i przekroju
i przekroju ![]() , wzdłuż której przemieszcza się pewna substancja
, wzdłuż której przemieszcza się pewna substancja ![]() . Rurka jest na tyle wąska, że ruch cząsteczek odbywa się tylko wzdłuż niej.
Niech stężenie cząsteczek tej substancji w chwili
. Rurka jest na tyle wąska, że ruch cząsteczek odbywa się tylko wzdłuż niej.
Niech stężenie cząsteczek tej substancji w chwili ![]() w miejscu
w miejscu ![]() wynosi
wynosi ![]() i załóżmy, że
i załóżmy, że ![]() jest dostatecznie gładką funkcją obu zmiennych.
jest dostatecznie gładką funkcją obu zmiennych.
Z punktem ![]() związujemy wycinek rurki
związujemy wycinek rurki ![]() o objętości
o objętości ![]() . Zmiana stężenia substancji
. Zmiana stężenia substancji ![]() w tym wycinku następuje wyniku przepływu — mamy z jednej strony napływ do wycinka, z drugiej odpływ z niego. Zgodnie z prawem Ficka masa substancji przepływająca przez wąski przekrój w ciągu krótkiego przedziału czasu
w tym wycinku następuje wyniku przepływu — mamy z jednej strony napływ do wycinka, z drugiej odpływ z niego. Zgodnie z prawem Ficka masa substancji przepływająca przez wąski przekrój w ciągu krótkiego przedziału czasu ![]() jest proporcjonalna do gradientu stężenia (w naszym jednowymiarowym przypadku do
jest proporcjonalna do gradientu stężenia (w naszym jednowymiarowym przypadku do ![]() ), długości przedziału czasu i pola przekroju rurki, zatem
), długości przedziału czasu i pola przekroju rurki, zatem
w punkcie ![]() oraz
oraz
w punkcie ![]() , gdzie
, gdzie ![]() jest pewnym współczynnikiem proporcjonalności. Zatem zmiana masy w objętości
jest pewnym współczynnikiem proporcjonalności. Zatem zmiana masy w objętości ![]() wynosi
wynosi ![]() , czyli zmiana stężenia substancji w wycinku wyraża się wzorem
, czyli zmiana stężenia substancji w wycinku wyraża się wzorem
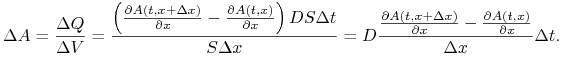 |
Stąd, dzieląc stronami powyższą równość przez ![]() i przechodząc do granicy
i przechodząc do granicy ![]() oraz
oraz ![]() dostajemy
dostajemy
| (11.1) |
czyli jednowymiarowe równanie dyfuzji. W ogólnym przypadku równanie dyfuzji ma postać
gdzie
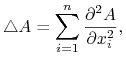 |
![]() oznacza wymiar przestrzeni (w przypadku procesów obserwowanych w naturze mamy
oznacza wymiar przestrzeni (w przypadku procesów obserwowanych w naturze mamy ![]() lub
lub ![]() ) i
) i ![]() nazywamy operatorem Laplace'a lub krócej laplasjanem, a
nazywamy operatorem Laplace'a lub krócej laplasjanem, a ![]() — współczynnikiem dyfuzji.
— współczynnikiem dyfuzji.
Z naszego populacyjnego punktu widzenia będziemy rozpatrywać dyfuzję jako proces losowego przemieszczania się osobników w przestrzeni. Najprostsze podejście do tego typu zagadnień reprezentowane jest przez tzw. ruchy Browna. Ponownie dla uproszczenia omówimy sytuację jednowymiarową. Rozważamy prostą podzieloną na odcinki o długości ![]() . Niech osobnik znajduje się w chwili
. Niech osobnik znajduje się w chwili ![]() w odcinku
w odcinku ![]() i w przedziale czasu o długości
i w przedziale czasu o długości ![]() może się przemieścić do odcinka na lewo, na prawo, albo pozostać w tym samym odcinku. Załóżmy, że prawdopodobieństwo przemieszczenia się do odcinka
może się przemieścić do odcinka na lewo, na prawo, albo pozostać w tym samym odcinku. Załóżmy, że prawdopodobieństwo przemieszczenia się do odcinka ![]() wynosi
wynosi ![]() , a do odcinka
, a do odcinka ![]() —
— ![]() . Niech
. Niech ![]() będzie liczbą osobników w chwili
będzie liczbą osobników w chwili ![]() w odcinku
w odcinku ![]() . Po upływie czasu
. Po upływie czasu ![]() w tym samym odcinku mamy
w tym samym odcinku mamy
| (11.2) |
gdzie ![]() oznacza średnią liczbę osobników, które w czasie
oznacza średnią liczbę osobników, które w czasie ![]() były na lewo od rozpatrywanego odcinka i przemieściły do niego,
były na lewo od rozpatrywanego odcinka i przemieściły do niego, ![]() to osobniki, które były na prawo i przeszły na lewo, natomiast
to osobniki, które były na prawo i przeszły na lewo, natomiast ![]() ,
, ![]() odpowiadają tym osobnikom, które były w omawianym odcinku w czasie
odpowiadają tym osobnikom, które były w omawianym odcinku w czasie ![]() i w
przedziale czasu
i w
przedziale czasu ![]() przemieściły się odpowiednio na prawo lub lewo. Załóżmy teraz, że funkcję
przemieściły się odpowiednio na prawo lub lewo. Załóżmy teraz, że funkcję ![]() możemy rozwinąć w szereg Taylora w punkcie
możemy rozwinąć w szereg Taylora w punkcie ![]() zarówno jako funkcję zmiennej
zarówno jako funkcję zmiennej ![]() z parametrem
z parametrem ![]() , jak i zmiennej
, jak i zmiennej ![]() z parametrem
z parametrem ![]() . Otrzymujemy odpowiednio
. Otrzymujemy odpowiednio
Wstawiając powyższe rozwinięcia do równania (11.2) dostajemy
Załóżmy teraz, że ![]() , czyli osobnik z jednakowym prawdopodobieństwem przemieszcza się zarówno w lewo, jak i w prawo. Mamy wtedy
, czyli osobnik z jednakowym prawdopodobieństwem przemieszcza się zarówno w lewo, jak i w prawo. Mamy wtedy
Dzieląc to równanie przez ![]() , przechodząc do granicy
, przechodząc do granicy ![]() i
i ![]() w taki sposób, że
w taki sposób, że ![]() dostajemy równanie (11.1).
dostajemy równanie (11.1).
Otrzymaliśmy więc związek losowego przemieszczenia się osobników z równaniem dyfuzji z jednej strony i pewnym łańcuchem Markowa z drugiej.
11.1. Równania ewolucyjne: równanie Fishera – Kołmogorowa
W przypadku rzeczywistych populacji oprócz przemieszczania się rozpatrujemy zwykle także inne procesy, np. rozrodczości/śmiertelności. W ogólnym przypadku otrzymujemy równanie reakcji-dyfuzji
| (11.3) |
zwane także równaniem ewolucyjnym, które opisuje zmiany zagęszczenia populacji w chwili ![]() w miejscu o położeniu
w miejscu o położeniu ![]() w przestrzeni. Czasami także w odniesieniu do funkcji
w przestrzeni. Czasami także w odniesieniu do funkcji ![]() używa się nazwy kinetyka oddziaływań (albo reakcji w kontekście biochemicznym), a odpowiadające równaniu (11.3) równanie zwyczajne
używa się nazwy kinetyka oddziaływań (albo reakcji w kontekście biochemicznym), a odpowiadające równaniu (11.3) równanie zwyczajne ![]() zwane jest wtedy równaniem kinetycznym.
zwane jest wtedy równaniem kinetycznym.
Równanie Skellama
Najprostsze tego typu równanie z liniową kinetyką zostało użyte przez Skellama w 1951 roku do opisu rozprzestrzeniania się populacji. Dokładniej, za pomocą równania (11.3) z funkcją ![]() opisał on rozprzestrzenianie się populacji piżmaków w Europie. Gatunek ten został sprowadzony do Europy w 1905 roku przez węgierskiego posiadacza ziemskiego i szybko rozprzestrzenił się wokół. Mimo że obszar Europy jest ograniczony, Skellam rozpatrywał to równanie w całym
opisał on rozprzestrzenianie się populacji piżmaków w Europie. Gatunek ten został sprowadzony do Europy w 1905 roku przez węgierskiego posiadacza ziemskiego i szybko rozprzestrzenił się wokół. Mimo że obszar Europy jest ograniczony, Skellam rozpatrywał to równanie w całym ![]() z warunkiem początkowym, który odpowiada introdukcji kilku osobników w punkcie
z warunkiem początkowym, który odpowiada introdukcji kilku osobników w punkcie ![]() , czyli
, czyli ![]() , gdzie
, gdzie ![]() to początkowa liczba osobników, a
to początkowa liczba osobników, a ![]() , gdzie
, gdzie ![]() oznacza deltę-Diraca, czyli
oznacza deltę-Diraca, czyli ![]() dla
dla ![]() oraz
oraz ![]() . Aby prześledzić rozprzestrzenianie się osobników zgodnie z modelem Skellama zbadajmy najpierw zagadnienie prostsze.
. Aby prześledzić rozprzestrzenianie się osobników zgodnie z modelem Skellama zbadajmy najpierw zagadnienie prostsze.
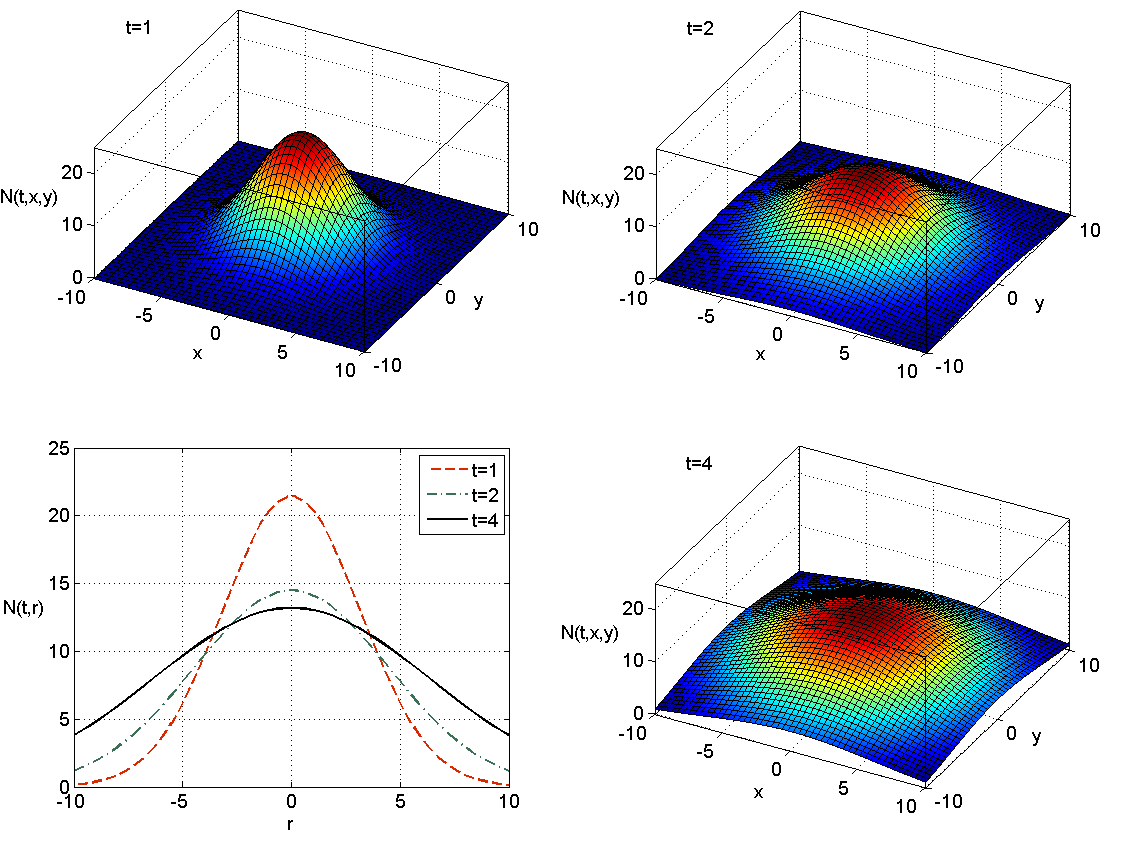
Rozpatrzmy równanie dyfuzji (11.1) w całym ![]() z warunkiem początkowym
z warunkiem początkowym ![]() , gdzie
, gdzie ![]() oznacza jednowymiarową deltę-Diraca. Można pokazać, że rozwiązaniem tego zagadnienia początkowego jest funkcja
oznacza jednowymiarową deltę-Diraca. Można pokazać, że rozwiązaniem tego zagadnienia początkowego jest funkcja
którą nazywamy rozwiązaniem fundamentalnym. Oczywiście spełnienie warunku początkowego należy rozumieć w sensie granicznym.
Ogólniej, jeśli rozważamy dyfuzję w przestrzeni ![]() -wymiarowej z warunkiem początkowym
-wymiarowej z warunkiem początkowym ![]() ,
, ![]() , to rozwiązanie fundamentalne ma postać
, to rozwiązanie fundamentalne ma postać
Teraz połączymy znajomość rozwiązania fundamentalnego równania dyfuzji dla ![]() i rozwiązania równania kinetycznego
i rozwiązania równania kinetycznego ![]() w celu otrzymania rozwiązania równania Skellama
w celu otrzymania rozwiązania równania Skellama
które zadaje falę inwazyjną. W punktach o ustalonym promieniu ![]() w pewnej chwili
w pewnej chwili ![]() pojawiają się osobniki, których tam wcześniej w zasadzie nie było (należy to interpretować w taki sposób, że fizycznie tych osobników nie było, mamy więc do czynienia z przełączeniem, przy czym funkcja
pojawiają się osobniki, których tam wcześniej w zasadzie nie było (należy to interpretować w taki sposób, że fizycznie tych osobników nie było, mamy więc do czynienia z przełączeniem, przy czym funkcja ![]() w sposób ciągły przybliża taką dynamikę), a choć ich liczebność wraz z upływem czasu maleje, ponieważ stale rozprzestrzeniają się dalej, to populacja jako taka w tym miejscu egzystuje, por rys. 11.1.
w sposób ciągły przybliża taką dynamikę), a choć ich liczebność wraz z upływem czasu maleje, ponieważ stale rozprzestrzeniają się dalej, to populacja jako taka w tym miejscu egzystuje, por rys. 11.1.
Równanie Fishera – Kołmogorowa
Równanie Fishera [3] lub inaczej Fishera – Kołmogorowa jest z kolei najprostszym nieliniowym równaniem typu ewolucyjnego i stanowi naturalne uogólnienie równania logistycznego na przypadek populacji złożonej z osobników, które mogą się przemieszczać i ruch ten ma znaczenie dla opisywanego procesu. Jest to także prototypowe równanie, w którym występują rozwiązania w postaci fal biegnących. Typowo jest to równanie rozpatrywane w całej przestrzeni ![]() , gdzie
, gdzie ![]() zwykle odpowiada naturalnym wymiarom
zwykle odpowiada naturalnym wymiarom ![]() ,
, ![]() lub
lub ![]() .
Zostało zaproponowane przez Fishera w 1937 roku do opisu rozprzestrzeniania się genu dominującego w populacji.
.
Zostało zaproponowane przez Fishera w 1937 roku do opisu rozprzestrzeniania się genu dominującego w populacji.
Równanie to ma postać
| (11.4) |
przy czym w najprostszym przypadku, który omówimy, ![]() ,
, ![]() , a
, a ![]() jest współczynnikiem dyfuzji.
jest współczynnikiem dyfuzji.
Pokażemy, że równanie (11.4) ma rozwiązania w postaci fal biegnących. Zaczniemy od przeprowadzenia ubezwymiarowienia w celu zredukowania liczby parametrów. Przeprowadzając zamianę zmiennych
i wracając do standardowych oznaczeń zmiennych dostajemy
| (11.5) |
Odpowiadające równaniu (11.5) równanie kinetyczne, czyli równanie logistyczne, ma dwa stany stacjonarne, niestabilny ![]() i stabilny
i stabilny ![]() . Będziemy więc poszukiwać fali biegnącej od
. Będziemy więc poszukiwać fali biegnącej od ![]() do
do ![]() .
.
Definicja 11.1
Falą biegnącą nazywamy nietrywialne, ograniczone rozwiązanie równania (11.3) postaci
dla pewnego ![]() , które nazywamy prędkością fali.
, które nazywamy prędkością fali.
Zauważmy, że
Uwaga 11.1
Równanie (11.1) nie ma rozwiązań w postaci fali biegnącej.
Załóżmy, że takie rozwiązanie ![]() istnieje. Skoro tak, to spełnia
równanie różniczkowe
istnieje. Skoro tak, to spełnia
równanie różniczkowe
zatem wartości własne tego równania spełniają równanie kwadratowe ![]() , czyli rozwiązania mają postać
, czyli rozwiązania mają postać ![]() , gdzie
, gdzie ![]() ,
, ![]() są stałymi. Ponieważ fala biegnąca jest ograniczona dla wszystkich
są stałymi. Ponieważ fala biegnąca jest ograniczona dla wszystkich ![]() , więc
, więc ![]() , czyli
, czyli ![]() , zatem nie jest to rozwiązanie w postaci fali.
, zatem nie jest to rozwiązanie w postaci fali.
Dla równania Fishera – Kołmogorowa (11.5) rozwiązanie w postaci fali biegnącej musi spełniać równanie
| (11.6) |
i postulujemy, że ![]() ,
, ![]() , zatem fala łączy dwa stany stacjonarne — jest odpychana od niestabilnego i przyciągana przez stabilny.
, zatem fala łączy dwa stany stacjonarne — jest odpychana od niestabilnego i przyciągana przez stabilny.
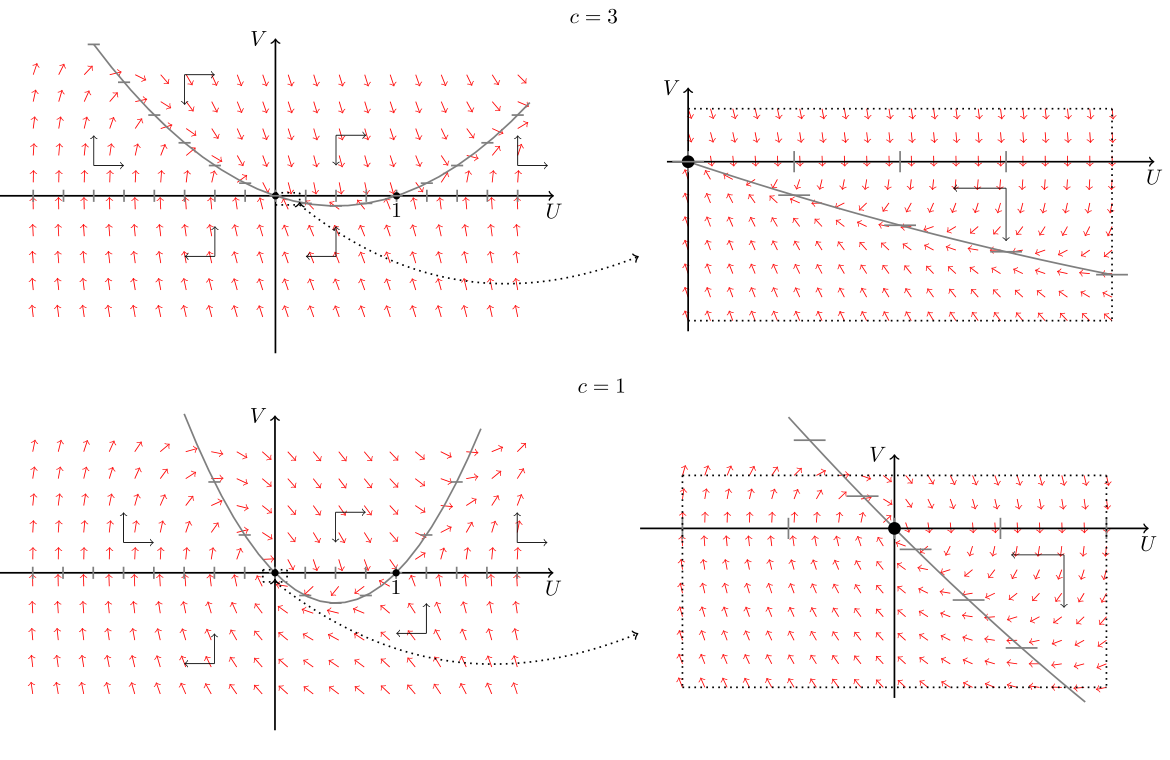
Równanie (11.6) jest równoważne układowi równań
| (11.7) |
gdzie prim (![]() ) oznacza różniczkowanie po
) oznacza różniczkowanie po ![]() . W przestrzeni fazowej
. W przestrzeni fazowej ![]() układ (11.7) ma oczywiście dwa punkty krytyczne
układ (11.7) ma oczywiście dwa punkty krytyczne ![]() oraz
oraz ![]() . Macierz Jacobiego tego układu ma postać
. Macierz Jacobiego tego układu ma postać
Badając lokalną stabilność wyznaczamy wielomian charakterystyczny
i wartości własne
skąd wynika, że ![]() jest zawsze punktem siodłowym, natomiast
jest zawsze punktem siodłowym, natomiast ![]() jest stabilnym ogniskiem dla
jest stabilnym ogniskiem dla ![]() i węzłem stabilnym dla
i węzłem stabilnym dla ![]() .
.
Stwierdzenie 11.1
Dla ![]() równanie (11.5) ma rozwiązanie w postaci fali biegnącej o prędkości
równanie (11.5) ma rozwiązanie w postaci fali biegnącej o prędkości ![]() .
.
Dla układu (11.7) przy ![]() z kierunku pola wektorowego łatwo wnioskujemy, że istnieje orbita łącząca punkt krytyczny
z kierunku pola wektorowego łatwo wnioskujemy, że istnieje orbita łącząca punkt krytyczny ![]() z punktem krytycznym
z punktem krytycznym ![]() , przy czym można pokazać, że pozostaje ona w dodatniej półpłaszczyźnie, por. rys. 11.2. Orbita ta tworzy rozwiązanie w postaci fali biegnącej łączącej punkty
, przy czym można pokazać, że pozostaje ona w dodatniej półpłaszczyźnie, por. rys. 11.2. Orbita ta tworzy rozwiązanie w postaci fali biegnącej łączącej punkty ![]() oraz
oraz ![]() .
.
Uwaga 11.2
Dla ![]() także istnieje orbita łącząca dwa punkty krytyczne
także istnieje orbita łącząca dwa punkty krytyczne ![]() i
i ![]() , ale ze względu na typ punktu
, ale ze względu na typ punktu ![]() nie jest zachowana nieujemność rozwiązań, zatem takie rozwiązania są nieistotne z biologicznego punktu widzenia, por. rys. 11.2.
nie jest zachowana nieujemność rozwiązań, zatem takie rozwiązania są nieistotne z biologicznego punktu widzenia, por. rys. 11.2.
Zagadnienie występowania fal biegnących (bądź też fal innego typu) jest często badane w kontekście tego typu równań. Należy jednak zdawać sobie sprawę z tego, że nie zawsze rozważana dziedzina jest na tyle duża, że można założyć iż jest to cała przestrzeń. Wtedy, przy założeniu ograniczonej dziedziny, rozważamy zagadnienia początkowo-brzegowe.
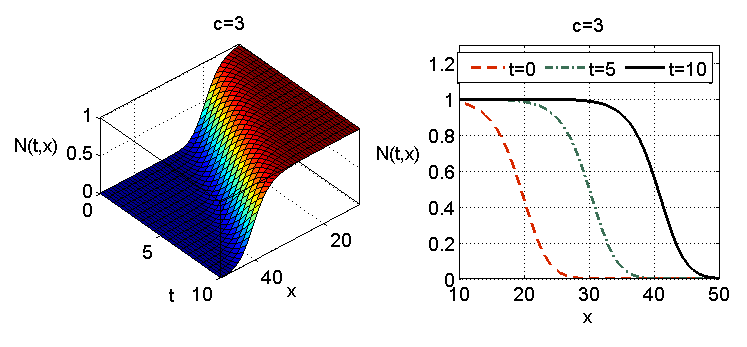
Równanie (11.4) było także rozpatrywane w kontekście rozwoju nowotworu przy założeniu warunku brzegowego. Załóżmy dla uproszczenia jednowymiarową propagację komórek na odcinku ![]() z warunkiem początkowym
z warunkiem początkowym
| (11.8) |
i warunkiem brzegowym Neumanna, czyli
| (11.9) |
Dla zagadnienia początkowo-brzegowego (11.4) (11.8) (11.9) lokalne istnienie i jednoznaczność wynika z własności kinetyki.
Korzystając z twierdzenia porównawczego 11.1 i własności rozwiązań równania logistycznego możemy wykazać, że dla warunku początkowego ![]() ,
, ![]() rozwiązanie zagadnienia początkowo-brzegowego (11.4) (11.8) (11.9) pozostaje w przedziale
rozwiązanie zagadnienia początkowo-brzegowego (11.4) (11.8) (11.9) pozostaje w przedziale ![]() .
.
Twierdzenie 11.1
Niech ![]() ,
, ![]() będą ograniczonymi funkcjami ciągłymi spełniającymi nierówności
będą ograniczonymi funkcjami ciągłymi spełniającymi nierówności
gdzie ![]() i
i ![]() oraz
oraz ![]() jest funkcją klasy
jest funkcją klasy ![]() . Załóżmy także, że
. Załóżmy także, że
-
jeśli
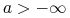 , to
, to![A\leq v(t,a)\leq u(t,a)\leq B\quad w\quad[0,T];](wyklady/mbm/mi/mi1060.png)
-
jeśli
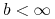 , to
, to![A\leq v(t,b)\leq u(t,b)\leq B\quad w\quad[0,T].](wyklady/mbm/mi/mi960.png)
Wtedy albo ![]() w
w ![]() , albo
, albo ![]() w
w ![]() .
.
Badając dynamikę modelu zwykle zaczynamy od zbadania stabilności rozwiązań stacjonarnych. Dla modeli niejednorodnych przestrzennie, oprócz rozważanych do tej pory rozwiązań stacjonarnych niezależnych od przestrzeni możemy mieć także rozwiązania stacjonarne, które zależą od położenia w dziedzinie równania. Jednak typowo analizę takiego zagadnienia zaczynamy od zbadania istnienia i stabilności rozwiązań stacjonarnych jednorodnych przestrzennie, a potem przechodzimy do znacznie trudniejszych zagadnień związanych z niejednorodnością przestrzenną. Jednym z takich zagadnień jest powstawanie tzw. wzorów Turinga — od strony analitycznej wiąże się to z bifurkacją stabilnego przestrzennie stanu stacjonarnego do niestabilnego, kiedy w otoczeniu stanu stacjonarnego powstają skupiska osobników — grupy o różnym zagęszczeniu — tworzące wzory przestrzenne.
Niech ![]() będzie odchyleniem rozwiązania równania (11.4)
od jednorodnego przestrzennie stanu stacjonarnego
będzie odchyleniem rozwiązania równania (11.4)
od jednorodnego przestrzennie stanu stacjonarnego ![]() (gdzie
(gdzie ![]() lub
lub ![]() ). Równanie zlinearyzowane wokół
). Równanie zlinearyzowane wokół ![]() ma postać
ma postać
| (11.10) |
gdzie ![]() dla stanu
dla stanu ![]() i
i ![]() dla stanu
dla stanu ![]() , przy czym
równanie (11.10) badamy z warunkiem brzegowym
, przy czym
równanie (11.10) badamy z warunkiem brzegowym ![]() i początkowym
i początkowym ![]() .
Z twierdzenia o linearyzacji wynika, że jeśli kinetyka jest funkcją różniczkowalną, to ze stabilności rozwiązania równania zlinearyzowanego wynika stabilność rozwiązania równania wyjściowego. Badając stabilność równania liniowego szukamy rozwiązań postaci
.
Z twierdzenia o linearyzacji wynika, że jeśli kinetyka jest funkcją różniczkowalną, to ze stabilności rozwiązania równania zlinearyzowanego wynika stabilność rozwiązania równania wyjściowego. Badając stabilność równania liniowego szukamy rozwiązań postaci ![]() , gdzie
, gdzie ![]() ,
, ![]() , jest rozwiązaniem fundamentalnym równania dyfuzji. Istnienie takiego rozwiązania wymaga spełnienia zależności
, jest rozwiązaniem fundamentalnym równania dyfuzji. Istnienie takiego rozwiązania wymaga spełnienia zależności
![]() . Zatem dla
. Zatem dla ![]() mamy
mamy ![]() , czyli
, czyli ![]() jest rozwiązaniem stabilnym, gdyż wszystkie wartości własne są ujemne, zaś dla
jest rozwiązaniem stabilnym, gdyż wszystkie wartości własne są ujemne, zaś dla ![]() mamy
mamy ![]() i przy
i przy ![]() wartość własna
wartość własna ![]() , zatem to rozwiązanie jest niestabilne. Dokładnie tak samo kształtuje się stabilność w przypadku bez dyfuzji, zatem dla równania Fishera – Kołmogorowa formowanie się wzorów Turinga nie jest możliwe. Co więcej widać, że aby takie wzory powstały, model musi być opisany za pomocą układu co najmniej dwóch równań.
, zatem to rozwiązanie jest niestabilne. Dokładnie tak samo kształtuje się stabilność w przypadku bez dyfuzji, zatem dla równania Fishera – Kołmogorowa formowanie się wzorów Turinga nie jest możliwe. Co więcej widać, że aby takie wzory powstały, model musi być opisany za pomocą układu co najmniej dwóch równań.
W przypadku równania (11.4) możemy udowodnić znacznie więcej, czyli globalną stabilność ![]() przy założeniu, że
przy założeniu, że ![]() jest oddzielone od zera.
jest oddzielone od zera.
Twierdzenie 11.2
Jeśli ![]() dla pewnego
dla pewnego ![]() oraz
oraz ![]() , to
, to ![]() przy
przy ![]() .
.
Twierdzenie porównawcze pokazuje, że ![]() dla
dla ![]() i
i ![]() . Jeśli
. Jeśli ![]() , to
, to
| (11.11) |
oraz ![]() dla
dla ![]() i
i ![]() . Zdefiniujmy
. Zdefiniujmy
![L(t)=\frac{1}{2}\int\limits _{{[0,1]}}\eta^{2}(t,x)dx.](wyklady/mbm/mi/mi916.png) |
Wtedy
![\dot{L}(t)=\int\limits _{{[0,1]}}\dot{\eta}(t,x)\eta(t,x)dx.](wyklady/mbm/mi/mi1078.png) |
Mnożąc równanie (11.11) przez ![]() i całkując przez części dostajemy
i całkując przez części dostajemy
![\dot{L}(t)=-r\int\limits _{{[0,1]}}\eta^{2}(t,x)dx-r\int\limits _{{[0,1]}}\eta^{3}(t,x)dx-D\int\limits _{{[0,1]}}\left(\frac{\partial\eta(t,x)}{\partial x}\right)^{2}dx.](wyklady/mbm/mi/mi969.png) |
Widzimy, że jeśli ![]() , to
, to ![]() oraz
oraz ![]() . Jeśli zaś
. Jeśli zaś ![]() , to
, to ![]() i
i ![]() , skąd wynika
, skąd wynika ![]() . W obu przypadkach
. W obu przypadkach ![]() przy
przy ![]() , skąd wynika
, skąd wynika ![]() .
.
11.2. Wzory Turinga
Jak już wspomnieliśmy, w przypadku jednego równania kinetycznego formowanie się wzorów Turinga nie jest możliwe, gdyż stabilność nie zmienia się pod wpływem dyfuzji. Natomiast dla ![]() istnieje taka możliwość. W szczególności można w taki sposób opisać tworzenie się wzorów umaszczenia u ssaków i próbować na tym gruncie wyjaśnić, dlaczego zebry czy żyrafy mają ustalony wzór umaszczenia, a u kotów domowych ten wzór jest zmienny. Podobnie — dlaczego wzór na tułowiu różni się od wzoru na kończynach lub ogonie. Taki model nazywamy modelem melanogenezy, ponieważ zakłada się, że za umaszczenie odpowiada stężenie barwnika zwanego melaniną. Melanina powstaje w reakcji substratu (tyrozyny) z enzymem (tyrozynazą). Model może być zatem opisany za pomocą układu dwóch równań reakcji-dyfuzji. Ponieważ w przypadku tułowia w uproszczeniu możemy powierzchnię skóry rozpatrywać jako pewną figurę płaską, to taki układ rozważa się najczęściej w ograniczonym obszarze w
istnieje taka możliwość. W szczególności można w taki sposób opisać tworzenie się wzorów umaszczenia u ssaków i próbować na tym gruncie wyjaśnić, dlaczego zebry czy żyrafy mają ustalony wzór umaszczenia, a u kotów domowych ten wzór jest zmienny. Podobnie — dlaczego wzór na tułowiu różni się od wzoru na kończynach lub ogonie. Taki model nazywamy modelem melanogenezy, ponieważ zakłada się, że za umaszczenie odpowiada stężenie barwnika zwanego melaniną. Melanina powstaje w reakcji substratu (tyrozyny) z enzymem (tyrozynazą). Model może być zatem opisany za pomocą układu dwóch równań reakcji-dyfuzji. Ponieważ w przypadku tułowia w uproszczeniu możemy powierzchnię skóry rozpatrywać jako pewną figurę płaską, to taki układ rozważa się najczęściej w ograniczonym obszarze w ![]() utożsamianym zwykle z prostokątem. Zadaje się zatem warunek początkowy oraz warunek brzegowy, który tu jest warunkiem Neumanna. Jeśli natomiast rozpatrujemy kończyny lub ogon, to rozpatrujemy taki układ np. na walcu lub stożku.
utożsamianym zwykle z prostokątem. Zadaje się zatem warunek początkowy oraz warunek brzegowy, który tu jest warunkiem Neumanna. Jeśli natomiast rozpatrujemy kończyny lub ogon, to rozpatrujemy taki układ np. na walcu lub stożku.
Badając możliwość występowania wzorów Turinga przeanalizujemy lokalną stabilność jednorodnych rozwiązań stacjonarnych w układzie dwóch równań reakcji-dyfuzji
| (11.12) |
gdzie ![]() ,
, ![]() , są stężeniami substancji chemicznych,
, są stężeniami substancji chemicznych, ![]() oznaczają tempa produkcji tych reakcji, a
oznaczają tempa produkcji tych reakcji, a ![]() są ich współczynnikami dyfuzji. W przypadku melanogenezy funkcje produkcji mają postać
są ich współczynnikami dyfuzji. W przypadku melanogenezy funkcje produkcji mają postać
gdzie ![]() to stężenie tyrozyny, a
to stężenie tyrozyny, a ![]() — tyrozynazy. Zauważmy, że dla
— tyrozynazy. Zauważmy, że dla ![]() nieliniowy składnik
nieliniowy składnik ![]() ma postać funkcji Michaelisa – Menten, natomiast dla
ma postać funkcji Michaelisa – Menten, natomiast dla ![]() wraz z rosnącą ilością substratu reakcja ulega zahamowaniu.
wraz z rosnącą ilością substratu reakcja ulega zahamowaniu.
Dla uproszczenia układ (11.12) będziemy rozpatrywać z jednorodnym warunkiem brzegowym Neumanna na ![]() — analiza w przypadku kwadratu
— analiza w przypadku kwadratu ![]() przebiega podobnie. Także dla uproszczenia założymy, że
przebiega podobnie. Także dla uproszczenia założymy, że ![]() jest jednorodnym stanem stacjonarnym układu (11.12) (jeśli stanem stacjonarnym jest
jest jednorodnym stanem stacjonarnym układu (11.12) (jeśli stanem stacjonarnym jest ![]() , to dokonujemy zamiany zmiennych
, to dokonujemy zamiany zmiennych ![]() ).
).
Badając stabilność stanu stacjonarnego zlinearyzujemy układ (11.12)
| (11.13) |
przy czym ![]() ,
, ![]() . Wzory Turinga mogą pojawić się w sytuacji, gdy w modelu bez dyfuzji, czyli dla
. Wzory Turinga mogą pojawić się w sytuacji, gdy w modelu bez dyfuzji, czyli dla ![]() stan stacjonarny jest stabilny, a dla pewnych
stan stacjonarny jest stabilny, a dla pewnych ![]() destabilizuje się.
destabilizuje się.
Okazuje się, że liniowe równanie (11.13) można rozwiązać metodą rozdzielenia zmiennych, czyli ![]() , gdzie
, gdzie ![]() to rozwiązanie układu kinetycznego (dla
to rozwiązanie układu kinetycznego (dla ![]() ), a
), a ![]() jest rozwiązaniem zagadnienia własnego operatora Laplace'a. W ogólnym przypadku na odcinku
jest rozwiązaniem zagadnienia własnego operatora Laplace'a. W ogólnym przypadku na odcinku ![]() takie rozwiązanie jest kombinacją sinusów i kosinusów, jednak ponieważ badamy układ (11.13) z warunkiem brzegowym Neumanna, to spełnia go tylko kosinus. Stąd
takie rozwiązanie jest kombinacją sinusów i kosinusów, jednak ponieważ badamy układ (11.13) z warunkiem brzegowym Neumanna, to spełnia go tylko kosinus. Stąd
| (11.14) |
Podstawiając postać rozwiązania (11.14) do układu (11.13) otrzymujemy
| (11.15) |
skąd dostajemy układ równań na współczynniki ![]() ,
, ![]()
| (11.16) |
Rozwiązanie dostajemy przyrównując wyznacznik układu (11.16) do 0
| (11.17) |
W przypadku bez dyfuzji równanie (11.17) ma postać
i stabilność stanu stacjonarnego zależy od śladu i wyznacznika macierzy Jacobiego układu kinetycznego. Precyzyjniej, jeśli
-
[I]
-
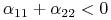 ,
, -
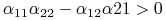 ,
,
to stan stacjonarny dla ![]() jest asymptotycznie stabilny. Jeśli teraz chcemy, by był on niestabilny dla
jest asymptotycznie stabilny. Jeśli teraz chcemy, by był on niestabilny dla ![]() , to któraś z powyższych nierówności powinna mieć przeciwny znak.
Nierówność I w przypadku z dyfuzją przyjmuje postać
, to któraś z powyższych nierówności powinna mieć przeciwny znak.
Nierówność I w przypadku z dyfuzją przyjmuje postać
![]() , więc dla dowolnych
, więc dla dowolnych ![]() jest spełniona przy założeniu
jest spełniona przy założeniu ![]() .
Zatem tylko nierówność II może zmienić znak dla
.
Zatem tylko nierówność II może zmienić znak dla ![]() . Postulując
. Postulując
dostajemy nierówność na ![]() , skąd otrzymujemy warunki destabilizacji stanu stacjonarnego pod wpływem dyfuzji
, skąd otrzymujemy warunki destabilizacji stanu stacjonarnego pod wpływem dyfuzji
-
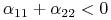 ,
,
-
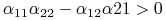 ,
, -
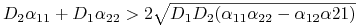 .
.
W analogiczny sposób możemy badać tworzenie się wzorów przestrzennych w modelu melanogenezy, przy czym wielkość i różnorodność formujących się wzorów zależy oczywiście od parametrów modelu. Jeśli dla danego gatunku dominują składniki kinetyczne, to powstające wzory są powtarzalne (jak np. u żyraf czy zebr), a jeśli składniki losowe, to wzory mogą się bardzo różnić w zależności od osobników (jak w przypadku kotów domowych).