Zagadnienia
14. Łańcuchy pokarmowe
Spróbujemy teraz zmierzyć się z problemem złożoności i stabilności ekosystemów w kontekście łańcuchów pokarmowych. Modelując łańcuchy pokarmowe skorzystamy z teorii grafów [6, 4]. Powszechnie uważa się, że bardziej stabilne są ekosystemy złożone, które na każdym poziomie troficznym mają wiele gatunków. Będziemy chcieli wyjaśnić te pojęcia ekologiczne w oparciu o podstawowe pojęcia teorii grafów. Wobec tego zaczniemy od wprowadzenia tych pojęć.
14.1. Podstawy teorii grafów
W teorii grafów wyróżniamy dwa podstawowe typy grafów — skierowane i nieskierowane. Ponieważ będziemy wykorzystywać oba te typy, więc zdefiniujemy je poniżej.
Definicja 14.1
Grafem nieskierowanym (krócej — grafem) ![]() nazywamy parę
nazywamy parę ![]() , gdzie zbiór
, gdzie zbiór ![]() nazywamy zbiorem wierzchołków, natomiast zbiór
nazywamy zbiorem wierzchołków, natomiast zbiór ![]() będący zbiorem nieuporządkowanych par elementów zbioru
będący zbiorem nieuporządkowanych par elementów zbioru ![]() nazywamy zbiorem krawędzi.
nazywamy zbiorem krawędzi.
Definicja 14.2
Grafem skierowanym ![]() nazywamy parę
nazywamy parę ![]() , gdzie
, gdzie ![]() jest zbiorem wierzchołków, natomiast
jest zbiorem wierzchołków, natomiast ![]() będący zbiorem par uporządkowanych elementów zbioru
będący zbiorem par uporządkowanych elementów zbioru ![]() nazywamy zbiorem krawędzi uporządkowanych.
nazywamy zbiorem krawędzi uporządkowanych.
Podkreślmy, że w teorii grafów nieskierowanych, którą będziemy się posługiwać, nie można połączyć dwóch wierzchołków więcej niż jedną krawędzią. Grafy nieskierowane z wieloma krawędziami opisuje teoria multigrafów. Natomiast w przypadku grafów skierowanych możemy mieć krawędź od stanu ![]() do stanu
do stanu ![]() oraz od stanu
oraz od stanu ![]() do stanu
do stanu ![]() . Z takimi grafami mamy do czynienia np. przy grafach przejścia łańcuchów Markowa, gdzie możemy z pewnym prawdopodobieństwem przejść ze stanu
. Z takimi grafami mamy do czynienia np. przy grafach przejścia łańcuchów Markowa, gdzie możemy z pewnym prawdopodobieństwem przejść ze stanu ![]() do stanu
do stanu ![]() jak i ze stanu
jak i ze stanu ![]() do stanu do stanu
do stanu do stanu ![]() .
.
Grafy są często wykorzystywane w teorii transportu, więc wiele pojęć w tej teorii nosi nazwy związane z przemieszczeniem się.
Definicja 14.3
Ścieżką w ![]() (odpowiednio w
(odpowiednio w ![]() ) nazywamy ciąg wierzchołków wraz z łączącymi je krawędziami:
) nazywamy ciąg wierzchołków wraz z łączącymi je krawędziami: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , gdzie
, gdzie ![]() (odpowiednio
(odpowiednio ![]() ) są krawędziami grafu
) są krawędziami grafu ![]() (odpowiednio
(odpowiednio ![]() ).
).
Definicja 14.4
Długością ścieżki nazywamy liczbę krawędzi ![]() w tej ścieżce.
w tej ścieżce.
Definicja 14.5
Ścieżką prostą nazywamy ścieżkę, w której każda krawędź występuje tylko raz: ![]() dla
dla ![]() .
.
Definicja 14.6
Ścieżkę nazywamy zamkniętą, jeśli zaczyna się i kończy w tym samym wierzchołku: ![]() .
.
Definicja 14.7
Ścieżkę prostą zamkniętą nazywamy cyklem.
Zauważmy, że ponieważ długość ścieżki ![]() , to w szczególności przy
, to w szczególności przy ![]() mamy ścieżkę
mamy ścieżkę ![]() , która ma długość
, która ma długość ![]() . Natomiast nie ma innych ścieżek łączących wierzchołek z samym sobą.
. Natomiast nie ma innych ścieżek łączących wierzchołek z samym sobą.
Ponieważ ścieżka jest w jednoznaczny sposób wyznaczona przez występujące w niej krawędzie, więc będziemy w skrócie pisać ![]() ,
, ![]() zamiast
zamiast ![]() ,
, ![]() ,
, ![]() .
.
Z istnieniem ścieżek łączy się też pojęcie osiągalności.
Definicja 14.8
Wierzchołek ![]() jest osiągalny z
jest osiągalny z ![]() w grafie
w grafie ![]() (odpowiednio
(odpowiednio ![]() ), jeśli istnieje ścieżka o początku w
), jeśli istnieje ścieżka o początku w ![]() i końcu w
i końcu w ![]() , czyli
ścieżka
, czyli
ścieżka ![]() ,
, ![]() .
.
Oczywiście w grafie nieskierowanym, jeśli ![]() jest osiągalne z
jest osiągalne z ![]() , to
, to ![]() jest osiągalne z
jest osiągalne z ![]() , natomiast w grafie skierowanym taka implikacja w ogólnym przypadku nie musi być prawdziwa. W związku z tym w przypadku grafu nieskierowanego możemy mówić o tym, że dwa wierzchołki komunikują się (lub są ze sobą połączone). Zauważmy też, że
, natomiast w grafie skierowanym taka implikacja w ogólnym przypadku nie musi być prawdziwa. W związku z tym w przypadku grafu nieskierowanego możemy mówić o tym, że dwa wierzchołki komunikują się (lub są ze sobą połączone). Zauważmy też, że
Twierdzenie 14.1
Jeśli w grafie ![]() wierzchołek
wierzchołek ![]() jest osiągalny z
jest osiągalny z ![]() , to istnieje ścieżka prosta z
, to istnieje ścieżka prosta z ![]() do
do ![]() .
.
Jeśli ![]() , to ścieżką prostą jest
, to ścieżką prostą jest ![]() . Jeśli
. Jeśli ![]() , to
skoro
, to
skoro ![]() jest osiągalny z
jest osiągalny z ![]() , to istnieje co najmniej jedna ścieżka
, to istnieje co najmniej jedna ścieżka ![]() ,
, ![]() ,
, ![]() . Załóżmy, że nie jest to ścieżka prosta. Wtedy istnieją takie indeksy
. Załóżmy, że nie jest to ścieżka prosta. Wtedy istnieją takie indeksy ![]() ,
, ![]() ,
, ![]() , że
, że ![]() . Zbudujmy nową ścieżkę
. Zbudujmy nową ścieżkę ![]() ,
, ![]() , biegnącą z
, biegnącą z ![]() do
do ![]() , usuwając krawędzie od indeksu
, usuwając krawędzie od indeksu ![]() do
do ![]() . Jeśli jest to ścieżka prosta, to kończymy dowód, jeśli nie, to powtarzamy poprzedni krok. Ponieważ liczba możliwych kroków jest skończona, to w którymś z kroków dostajemy ścieżkę prostą.
. Jeśli jest to ścieżka prosta, to kończymy dowód, jeśli nie, to powtarzamy poprzedni krok. Ponieważ liczba możliwych kroków jest skończona, to w którymś z kroków dostajemy ścieżkę prostą.
Korzystając z pojęcia długości ścieżki możemy teraz zdefiniować odległość dwóch wierzchołków.
Definicja 14.9
Jeśli wierzchołek ![]() jest osiągalny z
jest osiągalny z ![]() , to odległością z
, to odległością z ![]() do
do ![]() nazywamy długość najkrótszej ścieżki (czyli ścieżki o najmniejszej długości) z
nazywamy długość najkrótszej ścieżki (czyli ścieżki o najmniejszej długości) z ![]() do
do ![]() .
.
Zauważmy, że tak zdefiniowana odległość w grafie skierowanym nie spełnia wszystkich aksjomatów metryki, ponieważ nie musi być symetryczna. Co więcej, jeśli wierzchołek ![]() jest osiągalny z
jest osiągalny z ![]() , to nie oznacza, że
, to nie oznacza, że ![]() jest osiągalne z
jest osiągalne z ![]() , zatem odległość
, zatem odległość ![]() może być zdefiniowana, natomiast odległość
może być zdefiniowana, natomiast odległość ![]() — nie musi. Dla przykładu — w systemie komunikacyjnym miasta, jeśli wprowadzamy ulice jednokierunkowe, to musimy zadbać, żeby wszystkie istotne miejsca miały zdefiniowaną odległość.
— nie musi. Dla przykładu — w systemie komunikacyjnym miasta, jeśli wprowadzamy ulice jednokierunkowe, to musimy zadbać, żeby wszystkie istotne miejsca miały zdefiniowaną odległość.
Zauważmy dalej, że ![]() , ponieważ założyliśmy, że
, ponieważ założyliśmy, że ![]() jest ścieżką. Odległość w grafie nieskierowanym spełnia też nierówność trójkąta.
jest ścieżką. Odległość w grafie nieskierowanym spełnia też nierówność trójkąta.
Twierdzenie 14.2
Jeśli w grafie ![]() wierzchołek
wierzchołek ![]() jest osiągalny z
jest osiągalny z ![]() i
i ![]() jest osiągalny z
jest osiągalny z ![]() , to zachodzi
, to zachodzi
Z osiągalności wynika istnienie odpowiednich najkrótszych ścieżek
![]() długości
długości ![]() oraz
oraz ![]() długości
długości ![]() .
.
Wtedy ścieżka ![]() długości
długości ![]() zaczyna się w
zaczyna się w ![]() i kończy w
i kończy w ![]() , ale nie musi to być ścieżka najkrótsza. Zatem
, ale nie musi to być ścieżka najkrótsza. Zatem
14.2. Łańcuchy pokarmowe
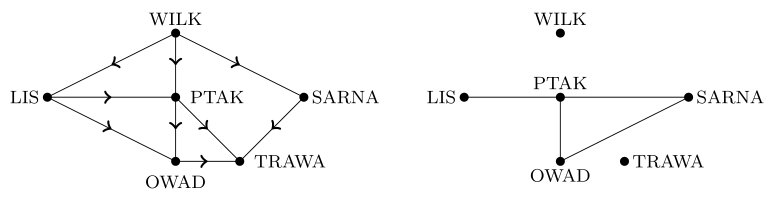
Teraz spróbujemy opisać ekosystem siedliska za pomocą łańcuchów pokarmowych. Siedliskiem nazwiemy obszar ograniczony i w pewien sposób wydzielony, w którym żyją różne gatunki roślin i zwierząt. Tworzą one łańcuch pokarmowy, który odzwierciedlamy za pomocą grafu skierowanego, w którym wierzchołkami są gatunki, natomiast krawędź skierowana prowadzi od gatunku ![]() do
do ![]() , jeśli
, jeśli ![]() jest drapieżnikiem dla
jest drapieżnikiem dla ![]() . Z danym łańcuchem pokarmowym związujemy też graf konkurencji, który z kolei stanowi graf nieskierowany z tymi samymi wierzchołkami, a krawędzie łączą dwa wierzchołki, jeśli odpowiadające im gatunki konkurują o to samo pożywienie.
. Z danym łańcuchem pokarmowym związujemy też graf konkurencji, który z kolei stanowi graf nieskierowany z tymi samymi wierzchołkami, a krawędzie łączą dwa wierzchołki, jeśli odpowiadające im gatunki konkurują o to samo pożywienie.
Łańcuchy pokarmowe możemy badać na różne sposoby. Przedstawimy tutaj koncepcję statusu troficznego (pokarmowego) zaadaptowaną z socjologicznej teorii organizacji. W ekologii socjologiczne pojęcie statusu osobnika w schemacie organizacji odpowiada poziomowi (stopniowi) troficznemu gatunku. Chcemy w taki sposób odzwierciedlić złożoność i różnorodność łańcuchów pokarmowych. Jeśli na każdym poziomie troficznym w danym łańcuchu pokarmowym jest wiele gatunków, to powiemy, że taki łańcuch jest różnorodny. Wspominaliśmy już, że w ekologii uważa się, iż łańcuchy bardziej złożone są też bardziej stabilne. Chcemy więc móc określić co to znaczy, że dany łańcuch jest bardziej złożony.
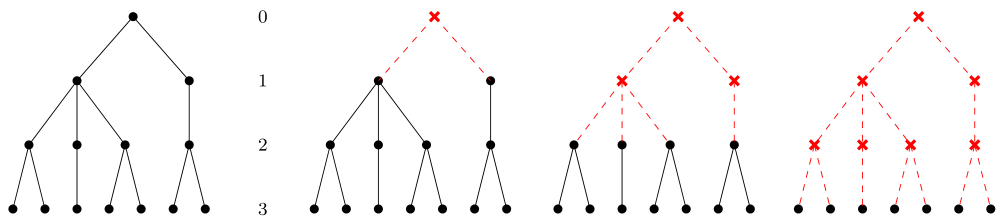
Pojęcie poziomu troficznego dość łatwo zdefiniować w przypadku prostych łańcuchów pokarmowych opisywanych za pomocą specyficznych grafów zwanych drzewami. W strukturze drzewa występuje jeden wyróżniony wierzchołek zwany korzeniem, do którego nie prowadzą żadne krawędzie wchodzące, zatem nie ma też żadnych ścieżek prowadzących od jakiegokolwiek innego wierzchołka do korzenia. Struktura drzewa jest rekurencyjna — jeśli usuniemy korzeń wraz z prowadzącymi zeń krawędziami, to powstaną oddzielne grafy o analogicznej strukturze, których korzeniami są wierzchołki bezpośrednio osiągalne z pierwotnego korzenia, por. rys. 14.2.
W takiej rekurencyjnej strukturze, jeśli procedurę usuwania korzeni przeprowadzimy dostatecznie wiele razy, to na końcu dostaniemy pojedyncze wierzchołki (czasem mówi się o liściach drzewa). Liczba usunięć przeprowadzająca dany wierzchołek na korzeń nowego grafu jest ściśle związana z poziomem troficznym gatunku reprezentowanego przez ten wierzchołek w drzewie. Jeśli maksymalna liczba możliwych usunięć w danym drzewie wynosi ![]() , a liczba usunięć, która tworzy z danego wierzchołka korzeń —
, a liczba usunięć, która tworzy z danego wierzchołka korzeń — ![]() , to poziom troficzny gatunku odpowiadającego temu wierzchołkowi równa się
, to poziom troficzny gatunku odpowiadającego temu wierzchołkowi równa się ![]() .
.
W ogólnym przypadku dla złożonego łańcucha pokarmowego znacznie trudniej zdefiniować analog tego pojęcia. Zdefiniujemy miarę statusu troficznego w celu odróżnienia od ,,zwykłego” poziomu troficznego, łatwego do wyznaczenia w prostych strukturach. Zanim przejdziemy do zaproponowania takiej definicji wprowadzimy odpowiednie założenia. Zakładamy, że graf opisujący łańcuch pokarmowy jest acykliczny, czyli wśród ścieżek tego grafu nie da się wyróżnić cyklu. W szczególności nie ma dwóch gatunków ![]() i
i ![]() , takich że jednocześnie
, takich że jednocześnie ![]() jest drapieżnikiem dla
jest drapieżnikiem dla ![]() i
i ![]() jest drapieżnikiem dla
jest drapieżnikiem dla ![]() . Dla takich grafów sformułujemy system aksjomatów, którym powinna podlegać miara statusu troficznego. Zauważmy, że w zależności od liczby przyjętych aksjomatów odpowiadająca im miara może być jednoznaczna, niejednoznaczna (przy mniejszej liczbie aksjomatów), a nawet może nie istnieć, jeśli aksjomatów jest zbyt dużo.
Odpowiednia liczba aksjomatów z jednej strony prowadzi do barku możliwości wyboru i implikuje jednoznaczność miary, z drugiej — gwarantuje jej istnienie. Jeśli dany układ aksjomatów jest zbyt obszerny i odpowiadająca mu miara nie istnieje, to należy się zastanowić, które z aksjomatów należy usunąć, aby zagwarantować istnienie i jednocześnie nie usunąć zbyt wielu aksjomatów.
. Dla takich grafów sformułujemy system aksjomatów, którym powinna podlegać miara statusu troficznego. Zauważmy, że w zależności od liczby przyjętych aksjomatów odpowiadająca im miara może być jednoznaczna, niejednoznaczna (przy mniejszej liczbie aksjomatów), a nawet może nie istnieć, jeśli aksjomatów jest zbyt dużo.
Odpowiednia liczba aksjomatów z jednej strony prowadzi do barku możliwości wyboru i implikuje jednoznaczność miary, z drugiej — gwarantuje jej istnienie. Jeśli dany układ aksjomatów jest zbyt obszerny i odpowiadająca mu miara nie istnieje, to należy się zastanowić, które z aksjomatów należy usunąć, aby zagwarantować istnienie i jednocześnie nie usunąć zbyt wielu aksjomatów.
Wprowadzając system aksjomatów analogiczny do systemu aksjomatów dla struktury organizacji posłużymy się pojęciami bezpośredniego i pośredniego drapieżnika (analogicznie bezpośredniej i pośredniej ofiary). Powiemy, że gatunek ![]() jest bezpośrednim drapieżnikiem dla
jest bezpośrednim drapieżnikiem dla ![]() jeśli istnieje krawędź z
jeśli istnieje krawędź z ![]() do
do ![]() , natomiast jest pośrednim drapieżnikiem, jeśli
, natomiast jest pośrednim drapieżnikiem, jeśli ![]() jest osiągalne z
jest osiągalne z ![]() .
Będziemy mówić, że
.
Będziemy mówić, że ![]() jest drapieżnikiem dla
jest drapieżnikiem dla ![]() , jeśli
, jeśli ![]() albo bezpośrednim, albo pośrednim drapieżnikiem dla
albo bezpośrednim, albo pośrednim drapieżnikiem dla ![]() .
Analogicznie
.
Analogicznie ![]() jest wtedy ofiarą
jest wtedy ofiarą ![]() (bezpośrednią/pośrednią).
Zauważmy, że w dowolnym łańcuchu pokarmowym możliwa jest sytuacja, gdy ani
(bezpośrednią/pośrednią).
Zauważmy, że w dowolnym łańcuchu pokarmowym możliwa jest sytuacja, gdy ani ![]() nie jest drapieżnikiem dla
nie jest drapieżnikiem dla ![]() , ani
, ani ![]() nie jest drapieżnikiem dla
nie jest drapieżnikiem dla ![]() .
.
Jeśli ![]() jest drapieżnikiem dla
jest drapieżnikiem dla ![]() , to zdefiniujmy
, to zdefiniujmy
Definicja 14.10
Stopień troficzny ![]() w stosunku do
w stosunku do ![]() równy odległości z
równy odległości z ![]() do
do ![]() .
.
Zauważmy, że powyższa definicja ma sens, gdyż ![]() jest w tym przypadku osiągalne z
jest w tym przypadku osiągalne z ![]() , co znaczy, że istnieje najkrótsza ścieżka z
, co znaczy, że istnieje najkrótsza ścieżka z ![]() do
do ![]() , długość której wyznacza odległość z
, długość której wyznacza odległość z ![]() do
do ![]() .
.
Niech ![]() oznacza miarę statusu troficznego gatunku
oznacza miarę statusu troficznego gatunku ![]() w łańcuchu pokarmowym
w łańcuchu pokarmowym ![]() . Spełnia ona następujące aksjomaty
. Spełnia ona następujące aksjomaty
-
[I.]
-
Jeśli gatunek
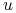 w łańcuchu
w łańcuchu 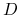 nie jest drapieżnikiem dla żadnego innego gatunku, to
nie jest drapieżnikiem dla żadnego innego gatunku, to 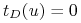 .
. -
Na bazie łańcucha
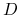 zbudujmy łańcuch
zbudujmy łańcuch 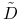 dodając nowy wierzchołek — gatunek, dla którego
dodając nowy wierzchołek — gatunek, dla którego 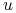 jest bezpośrednim drapieżnikiem. Wtedy
jest bezpośrednim drapieżnikiem. Wtedy 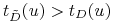 .
. -
Na bazie łańcucha
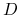 zbudujmy łańcuch
zbudujmy łańcuch 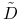 dodając wierzchołki lub krawędzie w taki sposób, że dla pewnych gatunków będących drapieżnikami wyróżnionego gatunku
dodając wierzchołki lub krawędzie w taki sposób, że dla pewnych gatunków będących drapieżnikami wyróżnionego gatunku 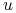 ich status troficzny względem
ich status troficzny względem 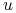 rośnie, nie ma natomiast takiego gatunku
rośnie, nie ma natomiast takiego gatunku 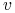 będącego ofiarą
będącego ofiarą 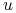 , dla którego by zmalał. Wtedy
, dla którego by zmalał. Wtedy 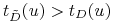 .
.
W strukturze organizacji aksjomat I oznacza, że jeśli dany pracownik nie ma żadnych podwładnych, to jego status jest równy ![]() . W aksjomacie II pracownikowi dajemy nowego bezpośredniego podwładnego, zatem status tego pracownika w organizacji wzrasta. Aksjomat III odzwierciedla sytuację awansu.
. W aksjomacie II pracownikowi dajemy nowego bezpośredniego podwładnego, zatem status tego pracownika w organizacji wzrasta. Aksjomat III odzwierciedla sytuację awansu.
Wykażemy teraz istnienie miary spełniającej aksjomaty I – III. Jest to dowód konstrukcyjny. Zdefiniujmy
| (14.1) |
gdzie ![]() jest liczbą gatunków na poziomie troficznym
jest liczbą gatunków na poziomie troficznym ![]() niżej względem
niżej względem ![]() .
.
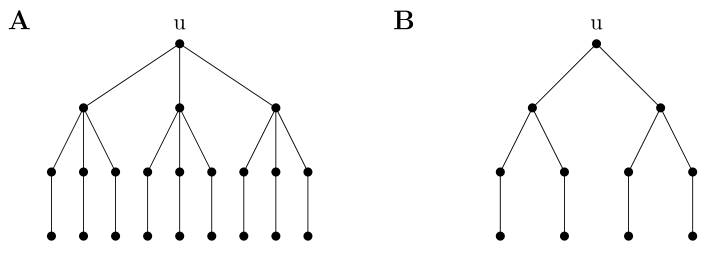
Zauważmy, że tak zdefiniowana miara różni się istotnie od proponowanej wcześniej miary reprezentowanej przez poziom troficzny dla drzew. Na rys. 14.3 możemy porównać te dwa pojęcia — korzeń ![]() będący na tym samym poziomie troficznym w obu drzewach ma różny status troficzny ze względu na zróżnicowanie w złożoności tych łańcuchów pokarmowych.
będący na tym samym poziomie troficznym w obu drzewach ma różny status troficzny ze względu na zróżnicowanie w złożoności tych łańcuchów pokarmowych.
Zauważmy dalej, że ![]() , co nie zostało założone w aksjomatach I – III. Jeśli do tych aksjomatów dołożymy postulat nieujemności, to miara
, co nie zostało założone w aksjomatach I – III. Jeśli do tych aksjomatów dołożymy postulat nieujemności, to miara ![]() jest minimalna w następującym sensie
jest minimalna w następującym sensie
Twierdzenie 14.3
Miara statusu troficznego ![]() określona wzorem (14.1) ma następujące własności
określona wzorem (14.1) ma następujące własności
-
[(a)]
-
spełnia aksjomaty I – III;
-
jeśli
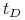 jest inną miarą o wartościach naturalnych spełniającą aksjomaty I – III, to dla dowolnego
jest inną miarą o wartościach naturalnych spełniającą aksjomaty I – III, to dla dowolnego 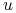 zachodzi
zachodzi 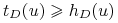 ;
;
Postać wzoru (14.1) implikuje, że aksjomaty I – III są spełnione w sposób oczywisty. W celu udowodnienia minimalności skorzystamy z następującego lematu
Lemat 14.1
W grafie skierowanym acyklicznym ![]() dla dowolnego wierzchołka
dla dowolnego wierzchołka ![]() istnieje taki
istnieje taki ![]() , który jest osiągalny z
, który jest osiągalny z ![]() i nie ma krawędzi wychodzących.
i nie ma krawędzi wychodzących.
Miara ![]() ma pewne niepożądane cechy. W szczególności mierząc status troficzny chcielibyśmy mieć następującą własność — jeśli
ma pewne niepożądane cechy. W szczególności mierząc status troficzny chcielibyśmy mieć następującą własność — jeśli ![]() jest miarą statusu troficznego i
jest miarą statusu troficznego i ![]() jest drapieżnikiem dla
jest drapieżnikiem dla ![]() , to chcielibyśmy by
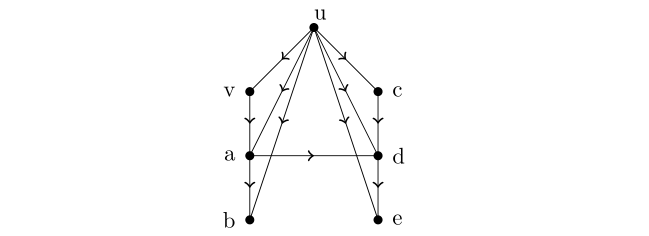
, to chcielibyśmy by ![]() . Niestety
. Niestety ![]() nie ma tej własności, por. rys. 14.4, gdzie
nie ma tej własności, por. rys. 14.4, gdzie ![]() jest bezpośrednim drapieżnikiem dla
jest bezpośrednim drapieżnikiem dla ![]() i jednocześnie
i jednocześnie ![]() .
.
W celu rozwiązania tego problemu musimy przedefiniować poziom troficzny gatunku ![]() względem gatunku
względem gatunku ![]() w łańcuchu pokarmowym. Do tej pory interpretowaliśmy to pojęcie w kontekście odległości od
w łańcuchu pokarmowym. Do tej pory interpretowaliśmy to pojęcie w kontekście odległości od ![]() do
do ![]() , czyli długości najkrótszej ścieżki, natomiast teraz przedefiniujemy je jako maksymalną długość ścieżki prostej prowadzącej z
, czyli długości najkrótszej ścieżki, natomiast teraz przedefiniujemy je jako maksymalną długość ścieżki prostej prowadzącej z ![]() do
do ![]() . Konstruując miarę statusu troficznego w oparciu o to pojęcie dostaniemy funkcję spełniającą aksjomaty I – III i dodatkowo aksjomat
. Konstruując miarę statusu troficznego w oparciu o to pojęcie dostaniemy funkcję spełniającą aksjomaty I – III i dodatkowo aksjomat
IV. Jeśli gatunek ![]() jest bezpośrednim/pośrednim drapieżnikiem dla
jest bezpośrednim/pośrednim drapieżnikiem dla ![]() , to
, to ![]() , gdzie
, gdzie ![]() jest miarą statusu troficznego gatunku
jest miarą statusu troficznego gatunku ![]() .
.
Twierdzenie 14.4
Zdefiniujmy miarę statusu troficznego ![]() względem
względem ![]() jako długość najdłuższej ścieżki prostej z
jako długość najdłuższej ścieżki prostej z ![]() do
do ![]() . Wtedy miara
. Wtedy miara ![]() zdefiniowana wzorem (14.1) spełnia aksjomaty I – IV.
zdefiniowana wzorem (14.1) spełnia aksjomaty I – IV.
Dowód tego faktu pozostawiamy jako ćwiczenie.
∎Wracając do łańcucha pokarmowego z ostatniego rysunku obliczamy teraz ![]() .
.
Miara statusu troficznego pozwala w pewnym sensie zbadać ważność danego gatunku w łańcuchu pokarmowym. Istnieje także inny sposób analizowania roli gatunku w ekosystemie i podatności ekosystemu na zmiany. Opiera się on na pojęciu spójności grafu.
Definicja 14.11
Graf skierowany ![]() nazwiemy
nazwiemy
-
silnie spójnym, jeśli dla dowolnych dwóch wierzchołków
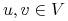 zarówno
zarówno 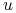 jest osiągalny z
jest osiągalny z 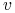 jak i
jak i 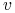 jest osiągalny z
jest osiągalny z 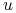 ;
; -
spójnym, jeśli dla dowolnej pary wierzchołków
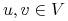 , albo
, albo 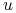 jest osiągalny z
jest osiągalny z 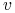 , albo
, albo 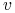 jest osiągalny z
jest osiągalny z 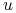 ;
; -
słabo spójnym, jeśli dla dowolnej pary wierzchołków
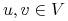 istnieje pseudościeżka między
istnieje pseudościeżka między 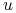 i
i 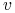 , czyli ciąg wierzchołków i krawędzi
, czyli ciąg wierzchołków i krawędzi 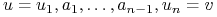 , takich że albo
, takich że albo 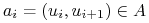 , albo
, albo 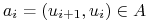 ;
; -
niespójnym, jeśli nie jest słabo spójny.
Oczywiście dla grafu nieskierowanego ![]() wszystkie trzy typy spójności pokrywają się, ponieważ ścieżka jest tożsama z pseudościeżką. Wobec tego graf nieskierowany
wszystkie trzy typy spójności pokrywają się, ponieważ ścieżka jest tożsama z pseudościeżką. Wobec tego graf nieskierowany ![]() jest spójny wtedy i tylko wtedy gdy dla każdej pary wierzchołków
jest spójny wtedy i tylko wtedy gdy dla każdej pary wierzchołków ![]() istnieje łącząca je ścieżka.
istnieje łącząca je ścieżka.
Z podanymi rodzajami spójności wiążemy pojęcie kategorii spójności grafu.
Definicja 14.12
Graf skierowany ![]() ma kategorię spójności
ma kategorię spójności
-
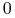 , jeśli jest niespójny;
, jeśli jest niespójny;
-
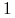 , jeśli jest słabo spójny i nie jest spójny;
, jeśli jest słabo spójny i nie jest spójny; -
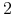 , jeśli jest spójny i nie jest silnie spójny;
, jeśli jest spójny i nie jest silnie spójny; -
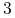 , jeśli jest silnie spójny.
, jeśli jest silnie spójny.
Okazuje się, że poszczególne kategorie spójności są równoważne istnieniu tzw. ścieżek kompletnych.
Definicja 14.13
Ścieżką kompletną w grafie ![]() (odpowiednio
(odpowiednio ![]() ) nazwiemy taką ścieżkę, która przechodzi przez wszystkie wierzchołki grafu
) nazwiemy taką ścieżkę, która przechodzi przez wszystkie wierzchołki grafu ![]() (
(![]() ), czyli
), czyli ![]() jest ścieżką kompletną, jeśli
jest ścieżką kompletną, jeśli ![]()
![]() , takie że
, takie że ![]() .
.
Można udowodnić następujące twierdzenie (dowód pomijamy).
Twierdzenie 14.5
Graf ![]() jest
jest
-
silnie spójny
 istnieje kompletna ścieżka zamknięta;
istnieje kompletna ścieżka zamknięta; -
spójny
 istnieje ścieżka kompletna;
istnieje ścieżka kompletna; -
słabo spójny
 istnieje kompletna pseudościeżka.
istnieje kompletna pseudościeżka.
Na bazie powyższych definicji wprowadzimy kategoryzację wierzchołków.
Definicja 14.14
Wierzchołek ![]() w grafie
w grafie ![]() nazwiemy wierzchołkiem kategorii
nazwiemy wierzchołkiem kategorii ![]() ,
, ![]() , gdy graf
, gdy graf ![]() ma kategorię spójności
ma kategorię spójności ![]() , a po usunięciu wierzchołka
, a po usunięciu wierzchołka ![]() ma kategorię
ma kategorię ![]() .
.
Dzięki temu pojęciu możemy klasyfikować gatunki w łańcuchu pokarmowym. Za krytyczne w danym ekosystemie uznamy takie gatunki, dla których różnica ![]() jest największa, czyli takie, których usunięcie powoduje największą zmianę spójności.
jest największa, czyli takie, których usunięcie powoduje największą zmianę spójności.
Na koniec omówimy pojęcie wrażliwości na zmiany w danym łańcuchu pokarmowym.
Definicja 14.15
Graf ![]() nazwiemy podatnym krawędziowo (wierzchołkowo), jeśli po usunięciu pewnej liczby krawędzi (wierzchołków) zmniejsza się kategoria spójności grafu. Stopniem podatności krawędziowej (wierzchołkowej) nazwiemy minimalną liczbę krawędzi (wierzchołków), usunięcie których powoduje zmianę kategorii spójności grafu.
nazwiemy podatnym krawędziowo (wierzchołkowo), jeśli po usunięciu pewnej liczby krawędzi (wierzchołków) zmniejsza się kategoria spójności grafu. Stopniem podatności krawędziowej (wierzchołkowej) nazwiemy minimalną liczbę krawędzi (wierzchołków), usunięcie których powoduje zmianę kategorii spójności grafu.
Zauważmy, że im większy stopień podatności, tym graf jest mniej wrażliwy na zmiany.
Podsumowując, dla danego łańcucha pokarmowego jego złożoność i stabilność będzie wyrażać się jak największą liczbą gatunków w ekosystemie z jak największą miarą statusu troficznego i jak największym stopniem podatności.