2. Modelowanie pojedynczej populacji II
2.1. Równanie logistyczne — model Verhulsta
Jak sprawdziliśmy, model Malthusa z emigracją nie rozwiązuje problemu ograniczonej pojemności siedliska. Wszystkie modele rozważane do tej pory bazują na modelu Malthusa, przy czym są liniowe. Teraz omówimy model zaproponowany ok. 1840 r. przez belgijskiego matematyka Pierre'a F. Verhulsta w [16], który jest prawdopodobnie pierwszym znanym w biologii populacyjnej modelem nieliniowym.
Model ten powstał w wyniku dyskusji grupy uczonych nad modelem Malthusa. Większość osób biorąca udział w tej dyskusji zgadzała się co do tego, że istnieją naturalne procesy, które hamują postulowany przez Malthusa geometryczny (nieograniczony) przyrost liczebności populacji. Według Verhulsta przyrost liczebności hamuje np. konkurencja o zasoby siedliska, która wiąże się w oczywisty sposób z ograniczonością tych zasobów. W związku z tym w równaniu (1.2) — które w dalszym ciągu będziemy utożsamiać z równaniem (1.4) dla ![]() — należy uwzględnić składnik opisujący konkurencję. W tym kontekście mówimy o konkurencji wewnątrzgatunkowej w odróżnieniu od konkurencji zewnątrzgatunkowej, występującej pomiędzy osobnikami różnych gatunków. Trzeba się więc zastanowić, jak reprezentować tę konkurencję w języku matematyki. Wszystkie modele biologiczne powstające w XIX (czy nawet w pierwszej połowie XX wieku) miały swoje korzenie w ugruntowanych już modelach fizycznych. Zatem nie należy się dziwić, że konkurencję między osobnikami tego samego gatunku Verhulst opisał w taki sam sposób jak losowe zderzenia cząsteczek gazu elementarnego. Liczba takich zderzeń jest proporcjonalna do kwadratu liczby cząstek
— należy uwzględnić składnik opisujący konkurencję. W tym kontekście mówimy o konkurencji wewnątrzgatunkowej w odróżnieniu od konkurencji zewnątrzgatunkowej, występującej pomiędzy osobnikami różnych gatunków. Trzeba się więc zastanowić, jak reprezentować tę konkurencję w języku matematyki. Wszystkie modele biologiczne powstające w XIX (czy nawet w pierwszej połowie XX wieku) miały swoje korzenie w ugruntowanych już modelach fizycznych. Zatem nie należy się dziwić, że konkurencję między osobnikami tego samego gatunku Verhulst opisał w taki sam sposób jak losowe zderzenia cząsteczek gazu elementarnego. Liczba takich zderzeń jest proporcjonalna do kwadratu liczby cząstek ![]() , a biorąc pod uwagę, że osobniki mogą konkurować ze sobą tylko wtedy, gdy się bezpośrednio zetkną można przyjąć, że konkurencja jest proporcjonalna do kwadratu liczebności, czyli równanie (1.2) zamienia się na
, a biorąc pod uwagę, że osobniki mogą konkurować ze sobą tylko wtedy, gdy się bezpośrednio zetkną można przyjąć, że konkurencja jest proporcjonalna do kwadratu liczebności, czyli równanie (1.2) zamienia się na
| (2.1) |
gdzie ![]() oznacza współczynnik konkurencji wewnątrzgatunkowej i odzwierciedla ,,szkodliwość” tej konkurencji dla populacji
oznacza współczynnik konkurencji wewnątrzgatunkowej i odzwierciedla ,,szkodliwość” tej konkurencji dla populacji ![]() .
.
To samo równanie możemy otrzymać na podstawie innego modelu heurystycznego. Wydaje się oczywiste, że przyjęty w modelu Malthusa (1.4) stały współczynnik reprodukcji ![]() stanowi często zbyt duże uproszczenie. Zwykle współczynnik ten zależy od wielu czynników, w tym także bezpośrednio od liczebności populacji. Jeśli liczebność jest niewielka, to osobniki mają dobry dostęp do zasobów siedliska i mogą się bez przeszkód rozmnażać, ale przy wzroście liczebności ten dostęp zmniejsza się. W takiej sytuacji przyrost per capita (czyli względny przyrost na jednego osobnika w populacji)
stanowi często zbyt duże uproszczenie. Zwykle współczynnik ten zależy od wielu czynników, w tym także bezpośrednio od liczebności populacji. Jeśli liczebność jest niewielka, to osobniki mają dobry dostęp do zasobów siedliska i mogą się bez przeszkód rozmnażać, ale przy wzroście liczebności ten dostęp zmniejsza się. W takiej sytuacji przyrost per capita (czyli względny przyrost na jednego osobnika w populacji)
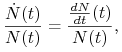 |
stały w modelu Malthusa (1.4), staje się funkcją zależną od ![]() . Ponieważ według naszych założeń reprodukcja zmniejsza się wraz ze wzrostem liczebności populacji, to najprostsze matematyczne odzwierciedlenie takiej zależności stanowi liniowa funkcja malejąca. Wobec tego
. Ponieważ według naszych założeń reprodukcja zmniejsza się wraz ze wzrostem liczebności populacji, to najprostsze matematyczne odzwierciedlenie takiej zależności stanowi liniowa funkcja malejąca. Wobec tego
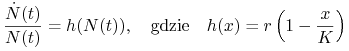 |
i przy ![]() równanie (2.1) i równanie logistyczne
równanie (2.1) i równanie logistyczne
| (2.2) |
pokrywają się. Nazwa ,,równanie logistyczne” wiąże się z typowym logistycznym kształtem części rozwiązań równania (2.2). Równanie to nazywa się często także równaniem Verhulsta lub równaniem Verhulsta – Pearla, przy czym nazwisko biologa R. Pearla pojawia się w tej nazwie w związku z zastosowaniami równania (2.2) do opisu konkretnych populacji.
Przejdziemy teraz do analizy przebiegu rozwiązań równania (2.2). Jak poprzednio jest to równanie o zmiennych rozdzielonych, które możemy rozwiązać korzystając z rozkładu ułamka ![]() na ułamki proste,
na ułamki proste,
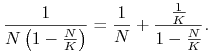 |
Naszym głównym zadaniem nie jest jednak poszukiwanie analitycznych rozwiązań budowanych modeli, tylko analiza własności i przebiegu tych rozwiązań.
Zauważmy, że prawa strona równania (2.2) jest funkcją klasy ![]() , co implikuje istnienie i jednoznaczność rozwiązań. Łatwo też sprawdzić, że dla
, co implikuje istnienie i jednoznaczność rozwiązań. Łatwo też sprawdzić, że dla ![]() mamy
mamy ![]() dla
dla ![]() . Jedną z metod tej wykazania tej własności stanowi zapisanie równania (2.2) w równoważnej postaci całkowej
. Jedną z metod tej wykazania tej własności stanowi zapisanie równania (2.2) w równoważnej postaci całkowej
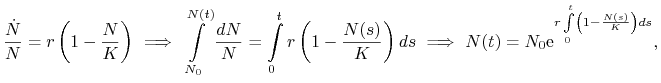 |
skąd od razu wynika nieujemność. Z kolei nieujemność implikuje oszacowanie
czyli wzrost jest co najwyżej wykładniczy i rozwiązanie istnieje dla wszystkich ![]() .
.
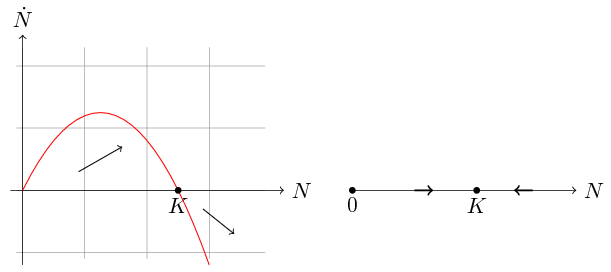
Zbadamy teraz zależność ![]() , która determinuje monotoniczność rozwiązań. Przyjrzyjmy się wykresowi funkcji
, która determinuje monotoniczność rozwiązań. Przyjrzyjmy się wykresowi funkcji ![]() , por. rys. 2.1.
Jest to parabola o miejscach zerowych
, por. rys. 2.1.
Jest to parabola o miejscach zerowych ![]() i
i ![]() skierowana w dół. Wynika stąd, że
skierowana w dół. Wynika stąd, że ![]() i
i ![]() są rozwiązaniami stacjonarnymi. Jeśli
są rozwiązaniami stacjonarnymi. Jeśli ![]() , to
, to ![]() , czyli rozwiązania dla warunku początkowego
, czyli rozwiązania dla warunku początkowego ![]() są rosnące i ograniczone, ponieważ z jednoznaczności rozwiązań wynika, że nie mogą przeciąć stacjonarnego rozwiązania
są rosnące i ograniczone, ponieważ z jednoznaczności rozwiązań wynika, że nie mogą przeciąć stacjonarnego rozwiązania ![]() . Zatem jeśli
. Zatem jeśli ![]() , to
, to
Analogicznie jeśli ![]() (rozwijająca się w naturalnych warunkach populacja nie może przekroczyć granicy
(rozwijająca się w naturalnych warunkach populacja nie może przekroczyć granicy ![]() , jak pokazaliśmy powyżej, czyli taka sytuacja jest możliwa jedynie w przypadku introdukcji osobników), to
, jak pokazaliśmy powyżej, czyli taka sytuacja jest możliwa jedynie w przypadku introdukcji osobników), to ![]() , więc dla takich wartości początkowych liczebność maleje i ponownie asymptotycznie osiąga wartość
, więc dla takich wartości początkowych liczebność maleje i ponownie asymptotycznie osiąga wartość ![]() . Jednak aby dokładniej przeanalizować przebieg rozwiązań musimy znać nie tylko wartość pierwszej pochodnej, ale także drugiej, która determinuje wypukłość/wklęsłość funkcji
. Jednak aby dokładniej przeanalizować przebieg rozwiązań musimy znać nie tylko wartość pierwszej pochodnej, ale także drugiej, która determinuje wypukłość/wklęsłość funkcji ![]() .
.
Obliczmy zatem
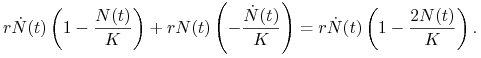 |
Widzimy, że jeśli rozwiązanie w pewnej chwili ![]() przyjmuje wartość
przyjmuje wartość ![]() , to zmienia się charakter przebiegu — funkcja
, to zmienia się charakter przebiegu — funkcja ![]() ma punkt przegięcia. Analizując znaki czynników
ma punkt przegięcia. Analizując znaki czynników ![]() i
i ![]() możemy wydzielić kilka obszarów, por. rys. 2.2
możemy wydzielić kilka obszarów, por. rys. 2.2
-
 , to
, to  rośnie do
rośnie do 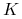 przy
przy 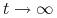 , więc istnieje
, więc istnieje 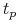 , takie że
, takie że 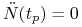 i
i 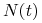 jest wypukła dla
jest wypukła dla 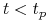 (szybki wzrost, porównywalny z wykładniczym, dla małych zagęszczeń), a wklęsła dla
(szybki wzrost, porównywalny z wykładniczym, dla małych zagęszczeń), a wklęsła dla 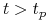 (następuje spowolnienie wzrostu dla większych zagęszczeń);
(następuje spowolnienie wzrostu dla większych zagęszczeń); -
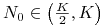 , wtedy funkcja
, wtedy funkcja 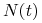 rośnie, ale wzrost jest powolny, funkcja
rośnie, ale wzrost jest powolny, funkcja 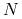 jest wklęsła;
jest wklęsła; -
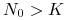 , co (należy ponownie podkreślić) odpowiada introdukcji osobników, wtedy
, co (należy ponownie podkreślić) odpowiada introdukcji osobników, wtedy 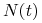 maleje w sposób wypukły do
maleje w sposób wypukły do 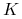 , zatem spadek liczebności jest dość szybki.
, zatem spadek liczebności jest dość szybki.
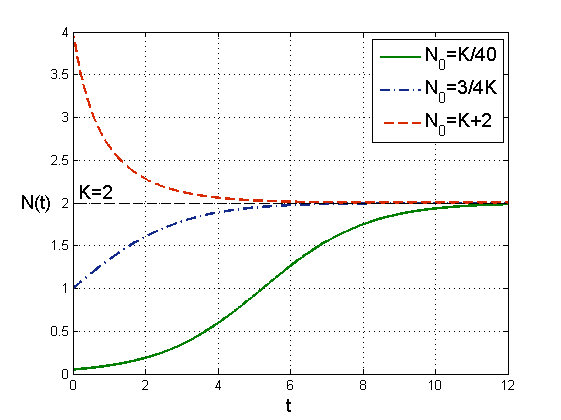
Widzimy więc, że dla ![]() rozwiązanie ma kształt wydłużonej litery S, jak krzywa logistyczna, która dobrze odzwierciedla wiele procesów, przebiegających w początkowej fazie szybko i intensywnie, a po pewnym czasie ulegających wysyceniu i stabilizujących się na maksymalnym dla danego procesu poziomie.
rozwiązanie ma kształt wydłużonej litery S, jak krzywa logistyczna, która dobrze odzwierciedla wiele procesów, przebiegających w początkowej fazie szybko i intensywnie, a po pewnym czasie ulegających wysyceniu i stabilizujących się na maksymalnym dla danego procesu poziomie.
2.2. Dyskretne równanie logistyczne
Często równolegle z modelem ciągłym rozważa się model dyskretny. Przedstawimy teraz dyskretną wersję równania (2.2). W tym celu przybliżymy pochodną ![]() ilorazem różnicowym
ilorazem różnicowym
założymy (analogicznie jak w przypadku modelu Malthusa), że ![]() jest równa hipotetycznej jednostce czasu
jest równa hipotetycznej jednostce czasu ![]() i zastosujemy notację dyskretną
i zastosujemy notację dyskretną ![]() ,
, ![]() . Otrzymujemy
. Otrzymujemy
| (2.3) |
gdzie ![]() i
i ![]() . Zauważmy, że o ile z biologicznego punktu widzenia mamy w równaniu logistycznym dwa parametry: współczynnik rozrodczości i pojemność siedliska, to z matematycznego punktu widzenia jeden z nich możemy z łatwością wyeliminować. Niech
. Zauważmy, że o ile z biologicznego punktu widzenia mamy w równaniu logistycznym dwa parametry: współczynnik rozrodczości i pojemność siedliska, to z matematycznego punktu widzenia jeden z nich możemy z łatwością wyeliminować. Niech ![]() . Dzieląc równanie (2.3) stronami przez
. Dzieląc równanie (2.3) stronami przez ![]() dostajemy
dostajemy
| (2.4) |
czyli model jednoparametrowy. Zauważmy, że model ten ma sens, o ile kolejne wyrazy ciągu ![]() pozostają w przedziale
pozostają w przedziale ![]() , ponieważ reprezentują one zagęszczenia populacji w proporcji do pojemności siedliska
, ponieważ reprezentują one zagęszczenia populacji w proporcji do pojemności siedliska ![]() . Wyrazy te obliczamy jako kolejne iteracje funkcji
. Wyrazy te obliczamy jako kolejne iteracje funkcji ![]() , która jest funkcją kwadratową z wartością maksymalną
, która jest funkcją kwadratową z wartością maksymalną ![]() . Zatem aby wszystkie wyrazy pozostawały w przedziale
. Zatem aby wszystkie wyrazy pozostawały w przedziale ![]() musi zachodzić
musi zachodzić ![]() . Będziemy więc badać dynamikę ciągu
. Będziemy więc badać dynamikę ciągu ![]() dla
dla ![]() i warunku początkowego
i warunku początkowego ![]() . Oczywiście jeśli
. Oczywiście jeśli ![]() albo
albo ![]() , to
, to ![]() dla
dla ![]() , więc interesujące są wartości
, więc interesujące są wartości ![]() .
.
Jeśli ciąg ![]() ma granicę, to równa się ona któremuś ze stanów stacjonarnych. Wyznaczmy więc te stany. Niech
ma granicę, to równa się ona któremuś ze stanów stacjonarnych. Wyznaczmy więc te stany. Niech ![]() oznacza stan stacjonarny. Wtedy
oznacza stan stacjonarny. Wtedy
Widzimy więc, że dodatni stan stacjonarny istnieje, o ile ![]() . Lokalną stabilność tych stanów badamy za pomocą wartości własnych przekształcenia
. Lokalną stabilność tych stanów badamy za pomocą wartości własnych przekształcenia ![]() . W naszym przypadku
. W naszym przypadku ![]() . Jeśli
. Jeśli ![]() , to stan stacjonarny jest wyznaczony jednoznacznie
, to stan stacjonarny jest wyznaczony jednoznacznie ![]() i
i ![]() , przy czym nierówność
, przy czym nierówność ![]() implikuje lokalną stabilność. Co więcej widzimy, że
implikuje lokalną stabilność. Co więcej widzimy, że ![]() , ponieważ
, ponieważ ![]() dla dowolnego
dla dowolnego ![]() przy założeniu
przy założeniu ![]() . Mamy więc ciąg malejący i ograniczony, czyli zbieżny, zatem stan
. Mamy więc ciąg malejący i ograniczony, czyli zbieżny, zatem stan ![]() jest globalnie stabilny w zbiorze
jest globalnie stabilny w zbiorze ![]() .
.
Jeśli ![]() , to istnieją dwa stany stacjonarne, przy czym
, to istnieją dwa stany stacjonarne, przy czym ![]() staje się niestabilny, gdyż teraz
staje się niestabilny, gdyż teraz ![]() . Dla dodatniego stanu stacjonarnego
. Dla dodatniego stanu stacjonarnego
![]() mamy
mamy ![]() oraz
oraz
Prostymi metodami, jak w przypadku zerowego stanu stacjonarnego pokazujemy, że dla ![]() ciąg
ciąg ![]() jest monotoniczny od pewnego miejsca, natomiast dla
jest monotoniczny od pewnego miejsca, natomiast dla ![]() możemy wyróżnić dwa podciągi monotoniczne od pewnego miejsca.
Faktycznie, jeśli
możemy wyróżnić dwa podciągi monotoniczne od pewnego miejsca.
Faktycznie, jeśli ![]() , to dla
, to dla ![]() zachodzi
zachodzi
![]() , natomiast dla
, natomiast dla ![]() mamy nierówność przeciwną. Oczywiście wystarczy rozpatrywać
mamy nierówność przeciwną. Oczywiście wystarczy rozpatrywać ![]() , gdyż wykres iterowanej funkcji
, gdyż wykres iterowanej funkcji ![]() jest symetryczny względem prostej
jest symetryczny względem prostej ![]() oraz
oraz ![]() , więc po pierwszej iteracji wyrazu
, więc po pierwszej iteracji wyrazu ![]() dostajemy
dostajemy ![]() . Wystarczy teraz wykazać, że jeśli
. Wystarczy teraz wykazać, że jeśli ![]() , to
, to ![]() . Nierówność
. Nierówność ![]() jest równoważna nierówności kwadratowej
jest równoważna nierówności kwadratowej
której wyróżnik ![]() i dla
i dla ![]() mamy dwa pierwiastki
mamy dwa pierwiastki ![]() oraz
oraz ![]() . Wobec tego nierówność ta jest spełniona dla
. Wobec tego nierówność ta jest spełniona dla ![]() . Analogicznie wykazujemy, że
. Analogicznie wykazujemy, że ![]() implikuje
implikuje ![]() . Mamy więc ciągi monotoniczne i ograniczone. Stosując tę samą technikę dowodzimy monotoniczności podciągów w przypadku
. Mamy więc ciągi monotoniczne i ograniczone. Stosując tę samą technikę dowodzimy monotoniczności podciągów w przypadku ![]() .
.
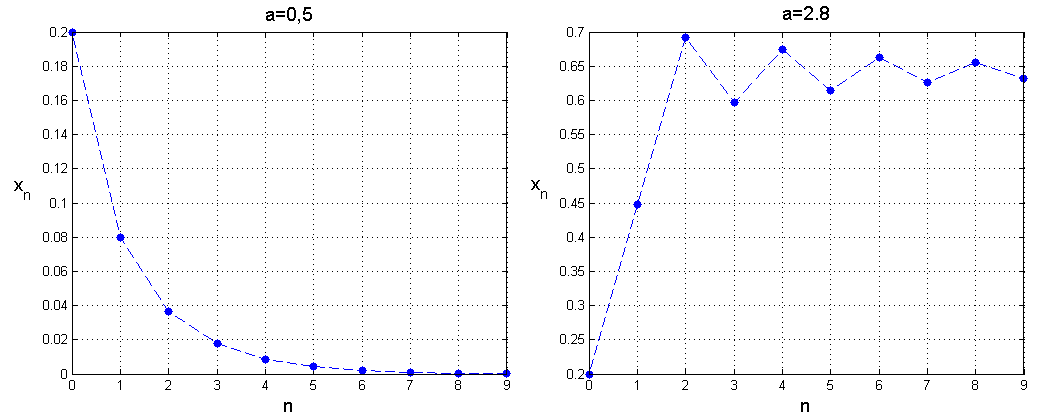
Dla omówionych wartości parametrów rozwiązania modelu dyskretnego są zbieżne, podobnie jak w przypadku modelu ciągłego, już dla tych wartości widzimy jednak zasadnicze różnice. Po pierwsze — dla małych ![]() rozwiązania dążą do
rozwiązania dążą do ![]() , czyli populacja wymiera. Nie należy się jednak temu dziwić, gdyż w modelu dyskretnym wartości współczynnika rozrodczości poniżej
, czyli populacja wymiera. Nie należy się jednak temu dziwić, gdyż w modelu dyskretnym wartości współczynnika rozrodczości poniżej ![]() odpowiadają procesowi śmiertelności, więc w tym przypadku model dyskretny opisuje sytuację, w której populacja wymiera nawet bez konkurencji, zatem jeśli konkurencja występuje, to sytuacja może się tylko pogorszyć. Przy
odpowiadają procesowi śmiertelności, więc w tym przypadku model dyskretny opisuje sytuację, w której populacja wymiera nawet bez konkurencji, zatem jeśli konkurencja występuje, to sytuacja może się tylko pogorszyć. Przy ![]() mamy monotoniczną zbieżność do dodatniego stanu stacjonarnego, zatem zachowanie jest analogiczne jak w modelu ciągłym, ale gdy
mamy monotoniczną zbieżność do dodatniego stanu stacjonarnego, zatem zachowanie jest analogiczne jak w modelu ciągłym, ale gdy ![]() przekracza
przekracza ![]() , pojawiają się gasnące oscylacje — takie zachowanie nie jest możliwe w modelu ciągłym. Co się dzieje, gdy
, pojawiają się gasnące oscylacje — takie zachowanie nie jest możliwe w modelu ciągłym. Co się dzieje, gdy ![]() przekracza
przekracza ![]() ?
?
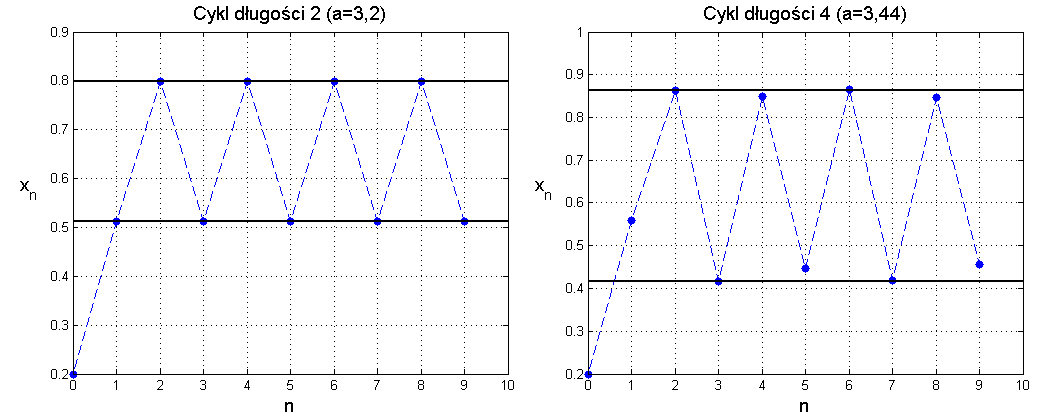
Dla ![]() oba rozwiązania stacjonarne stają się niestabilne. Możemy jednak sprawdzić, że po przekroczeniu tej wartości rozwiązania zyskują charakter stabilnego cyklu granicznego, najpierw o okresie
oba rozwiązania stacjonarne stają się niestabilne. Możemy jednak sprawdzić, że po przekroczeniu tej wartości rozwiązania zyskują charakter stabilnego cyklu granicznego, najpierw o okresie ![]() , potem o okresie
, potem o okresie ![]() itd. Cykl o okresie
itd. Cykl o okresie ![]() znajdujemy stosunkowo łatwo, jako rozwiązanie równania
znajdujemy stosunkowo łatwo, jako rozwiązanie równania
różne od znanych już stanów stacjonarnych. Szukamy więc dodatnich miejsc zerowych wielomianu
Dzielimy ![]() przez
przez ![]() i obliczamy
i obliczamy
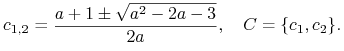 |
Zbiór ![]() jest poszukiwanym cyklem o okresie
jest poszukiwanym cyklem o okresie ![]() . Jego lokalną stabilność badamy znanymi już metodami. Dla
. Jego lokalną stabilność badamy znanymi już metodami. Dla ![]() cykl jest stabilny. Gdy
cykl jest stabilny. Gdy ![]() przekracza
przekracza ![]() następuje destabilizacja i pojawia się stabilny cykl o okresie
następuje destabilizacja i pojawia się stabilny cykl o okresie ![]() . Taką zmianę dynamiki rozwiązań nazywamy bifurkacją podwojenia okresu (albo bifurkacją rozwidleniową).
. Taką zmianę dynamiki rozwiązań nazywamy bifurkacją podwojenia okresu (albo bifurkacją rozwidleniową).
Wraz z rosnącym ![]() wyczerpują się okresy postaci
wyczerpują się okresy postaci ![]() . Przy przekroczeniu wartości krytycznej
. Przy przekroczeniu wartości krytycznej ![]() pojawiają się rozwiązania o innych okresach. Okresy te są związane z porządkiem Szarkowskiego. Na końcu bifurkuje orbita okresowa o okresie
pojawiają się rozwiązania o innych okresach. Okresy te są związane z porządkiem Szarkowskiego. Na końcu bifurkuje orbita okresowa o okresie ![]() , która powszechnie kojarzona jest z chaosem. Omawianie pojęcia chaosu wykracza poza ramy tego wykładu. Można jednak udowodnić, że dla
, która powszechnie kojarzona jest z chaosem. Omawianie pojęcia chaosu wykracza poza ramy tego wykładu. Można jednak udowodnić, że dla ![]() rozwiązania równania (2.4) są chaotyczne.
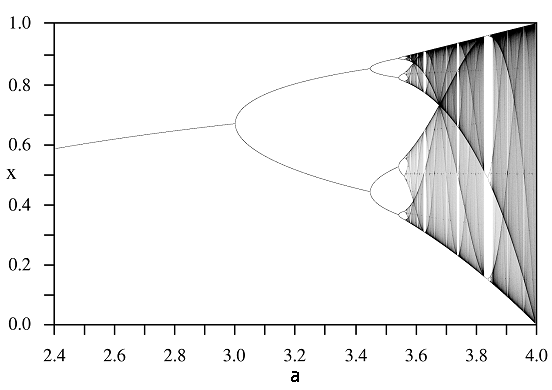
Cykl bifurkacji występujący w tym modelu najlepiej obrazuje diagram bifurkacyjny, zwany w tym przypadku drzewem Feigenbauma, por. rys. 2.5.
rozwiązania równania (2.4) są chaotyczne.
Cykl bifurkacji występujący w tym modelu najlepiej obrazuje diagram bifurkacyjny, zwany w tym przypadku drzewem Feigenbauma, por. rys. 2.5.
Drzewo Feigenbauma ma pewne własności obiektów zwanych fraktalami, w szczególności charakteryzuje się samopowtarzalnością — jeśli przybliżymy wycinek wykresu, to zobaczymy fragment łudząco podobny do całości. Podkreślić należy, że tego typu dynamikę generują wszystkie funkcje o własnościach podobnych do funkcji logistycznej, czyli ![]() unimodalne.
unimodalne.