Zagadnienia

3.1 Efekt Alleego
3.2 Funkcjonalna odpowiedź Hollinga i funkcja Hilla

3. Modelowanie pojedynczej populacji III

3.1. Efekt Alleego

W większości przypadków, jeśli nie uwzględniamy migracji, to model pojedynczej populacji $\mathcal{P}$ , zarówno w przypadku ciągłym jak i dyskretnym, możemy zapisać w ogólnej postaci

$\begin{split}&\dot{N}(t)=N(t)f(N(t))\ \text{--- model ciągły,}\\ &N_{{t+1}}=N_{t}f(N_{t})\ \text{--- model dyskretny},\end{split}$

(3.1)

gdzie $f$ odzwierciedla przyrost per capita, podobnie jak w przypadku równania logistycznego (2.2). Omówimy teraz postać funkcji $f$ w przypadku występowania w populacji tzw. efektu Alleego. Populacje, w których obserwujemy taki efekt, zmniejszają swoją liczebność, jeśli spadnie ona poniżej pewnego progu. Typowo wiążemy efekt Alleego z drapieżnictwem — na dynamikę danej populacji wpływa także to, że w ekosystemie występuje gatunek drapieżnika żywiący się osobnikami populacji $\mathcal{P}$ , przy czym zakładamy, że drapieżników jest zawsze dużo. Wobec tego jeśli liczebność populacji $\mathcal{P}$ jest niewielka, to drapieżniki zjadają dostępne osobniki i populacja $\mathcal{P}$ wymiera.

Modele z efektem Alleego mogą mieć różną postać, w zależności od funkcji drapieżnictwa. Najprostszy model stanowi modyfikację równania logistycznego (2.2)

$\dot{N}(t)=rN(t)\left(N(t)-N_{c}\right)\left(1-\frac{N(t)}{K}\right),\quad N_{c}\in(0,K),$

(3.2)

gdzie $r$ i $K$ interpretujemy analogicznie jak w równaniu logistycznym, natomiast $N_{c}$ nazywamy w tym kontekście pułapką drapieżnictwa.

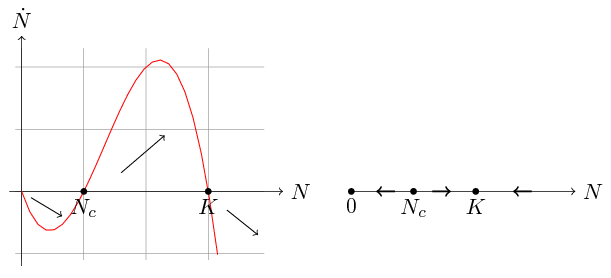
Podobnie jak w przypadku równania (2.2), równanie (3.2) możemy rozwiązać analitycznie rozkładając prawą stronę na ułamki proste, co zostawimy jako ćwiczenie. Najważniejsze własności rozwiązań odczytamy z portretu fazowego, por. rys. 3.1.

$Zależność $(N,\dot{N})$ dla modelu opisanego równaniem~\eqref{Allee} (po lewej) oraz odpowiadający tej zależności portret fazowy (po prawej).$

Rys. 3.1. Zależność $(N,\dot{N})$ dla modelu opisanego równaniem (3.2) (po lewej) oraz odpowiadający tej zależności portret fazowy (po prawej).

Widzimy, że prawa strona równania (3.2) jest wielomianem trzeciego stopnia o miejscach zerowych $0$ , $N_{c}$ , $K$ — są to oczywiście stany stacjonarne naszego równania — i ujemnym współczynniku przy $N^{3}$ . Wobec tego

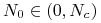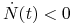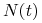dla $N_{0}\in\left(0,N_{c}\right)$ mamy $\dot{N}(t)<0$ , czyli $N(t)$ maleje do $0$ ;
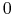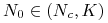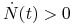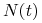dla $N_{0}\in\left(N_{c},K\right)$ mamy $\dot{N}(t)>0$ , czyli $N(t)$ rośnie do $K$ ;
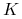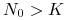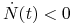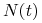dla $N_{0}>K$ mamy $\dot{N}(t)<0$ , czyli $N(t)$ maleje do $K$ .

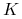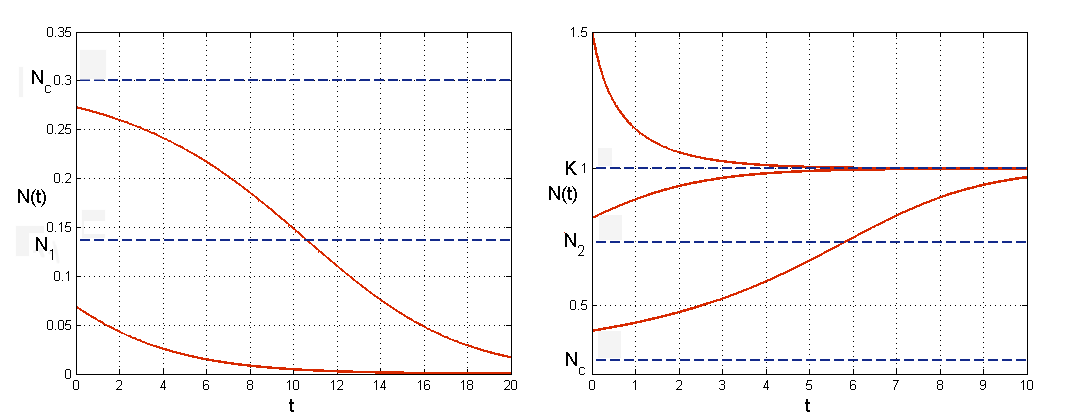
Policzymy też drugą pochodną, aby zbadać wklęsłość/wypukłość rozwiązań

$\ddot{N}(t)=-\frac{r}{K}\dot{N}(t)\left(3N^{2}(t)-2N(t)\left(N_{c}+K\right)+N_{c}K\right).$

Z kolei druga pochodna jest funkcją kwadratową zmiennej $N(t)$ o wyróżniku

$\Delta=4\left(K^{2}-N_{c}K+N_{c}^{2}\right)>0$

i pierwiastkach

$N_{1}=\tfrac{N_{c}+K-\sqrt{\Delta/4}}{3}\in\left(0,N_{c}\right),\quad N_{2}=\tfrac{N_{c}+K+\sqrt{\Delta/4}}{3}\in\left(N_{c},K\right).$

Ostatecznie, por. rys. 3.2,

dla 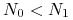$N_{0}<N_{1}$ funkcja 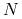$N$ maleje i 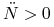$\ddot{N}>0$ , czyli 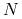$N$ jest wypukła;
dla 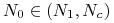$N_{0}\in\left(N_{1},N_{c}\right)$ funkcja 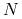$N$ maleje i pozostaje wklęsła dopóki 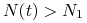$N(t)>N_{1}$ , w punkcie 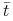$\bar{t}$ , takim że 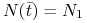$N(\bar{t})=N_{1}$ następuje zmiana charakteru przebiegu funkcji 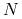$N$ — staje się ona wypukła;
dla 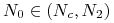$N_{0}\in\left(N_{c},N_{2}\right)$ przebieg jest symetryczny względem stanu stacjonarnego 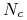$N_{c}$ do opisanego w poprzednim punkcie (podobny do przebiegu krzywych logistycznych);
dla 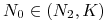$N_{0}\in\left(N_{2},K\right)$ funkcja 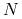$N$ rośnie w sposób wklęsły do stanu stacjonarnego $K$ ;
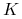dla 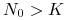$N_{0}>K$ funkcja 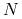$N$ maleje w sposób wypukły.

$Przykładowe wykresy rozwiązań równania~\eqref{Allee} dla różnych wartości początkowych $N_{0}$.$

Rys. 3.2. Przykładowe wykresy rozwiązań równania (3.2) dla różnych wartości początkowych $N_{0}$ .

Widzimy więc, że powyżej progu drapieżnictwa dynamika modelu jest analogiczna jak w przypadku równania logistycznego, por. prawy wykres na rys. 3.2, natomiast poniżej progu drapieżnictwa populacja wymiera, co widzimy na lewym wykresie na rys. 3.2.

3.2. Funkcjonalna odpowiedź Hollinga i funkcja Hilla

W dalszym ciągu będziemy zajmować się sytuacją, w której na opisywaną populację $\mathcal{P}$ ma wpływ drapieżnictwo. Wyprowadzimy wzór funkcji zwanej odpowiedzią funkcjonalną na obecność drapieżnika w oparciu o następujące rozumowanie zwane koncepcją dysku Hollinga [5]. Według tej koncepcji każdy drapieżnik polujący na danej powierzchni zauważa ofiary znajdujące się w obszarze o pewnym określonym promieniu $\gamma$ i promień ten jest charakterystyczny dla konkretnego gatunku drapieżnika. Spośród dostrzeżonych ofiar drapieżnik może upolować i zjeść pewną część. Zakładamy, że jest ona stała i oznaczamy tę część przez $\alpha$ . Każdy drapieżnik dzieli swój czas na dwa typy aktywności: wyszukiwanie ofiary oraz polowanie i zjadanie ofiary. Szukając ofiar drapieżnik przemieszcza się z pewną ustaloną prędkością $v$ , a polowanie i konsumpcja jednej ofiary zajmują mu średnio $T_{k}$ jednostek czasu.

Przy tych założeniach oszacujemy, ile średnio ofiar z populacji o zagęszczeniu $N$ zjada w jednostce czasu pojedynczy drapieżnik. Dowolny przedział czasu długości $T$ dzielimy na wymienione wyżej dwa typy aktywności, a za pomocą $T_{s}$ oznaczymy czas przeznaczony na wyszukiwanie ofiary. W czasie wyszukiwania drapieżnik poruszający się z prędkością $v$ obejmuje swoim zasięgiem powierzchnię $2\gamma vT_{s}$ , gdyż $vT_{s}$ to droga, którą przebywa drapieżnik, przy czym w każdym kroku rozglądając się widzi ofiary w odległości nie większej niż $\gamma$ w prawo i lewo. Zatem w przedziale czasu o długości $T$ drapieżnik chwyta i zjada $2\alpha\gamma vT_{s}N$ ofiar w czasie $2\alpha\gamma vT_{s}T_{k}N$ . Cały przedział czasu $T$ możemy więc zapisać jako

$T=T_{s}+2\alpha\gamma vT_{s}T_{k}N.$

Jeśli przez $f_{H}$ oznaczymy funkcję odpowiedzi drapieżnika, czyli

$f_{H}=\frac{\text{liczba ofiar zjedzona w czasie}\ T}{T},$

$f_{H}=\frac{2\alpha\gamma vT_{s}N}{T_{s}(1+2\alpha\gamma vT_{k}N)}$

i ostatecznie

$f_{H}=\frac{aN}{1+bN},$

(3.3)

gdzie $a=2\alpha\gamma v$ i $b=2\alpha\gamma vT_{k}$ , a równanie (3.3) nazywamy równaniem dysku Hollinga.

Zauważmy, że

$\lim\limits _{{N\to\infty}}f_{H}=\frac{1}{T_{k}},$

czyli nawet jeśli ofiar jest bardzo dużo, to drapieżnik nie może zjeść więcej niż pewną ich liczbę, określoną przez czas poświęcany na upolowanie i zjedzenie jednej ofiary. Jeśli rozpatrzymy skrajny przypadek, w którym $T_{k}\to 0$ przy ustalonej liczebności populacji ofiar, to

$\lim\limits _{{T_{k}\to 0}}f_{H}=aN,$

co oznacza, że w takim przypadku możemy odpowiedź funkcjonalną modelować za pomocą składnika liniowego. Taką postać odpowiedzi funkcjonalnej nazywamy odpowiedzią Hollinga I typu, która charakteryzuje się brakiem ograniczenia względem liczebności populacji ofiar, natomiast przy $b\ne 0$ mamy odpowiedź typu II, która jest ograniczona.

Wróćmy teraz do opisu dynamiki populacji $\mathcal{P}$ . Załóżmy, że na jej liczebność wpływa drapieżnictwo, odpowiedź funkcjonalną opisuje funkcja (3.3) i możemy przyjąć stałą liczebność drapieżników $D$ . Jeśli wewnętrzną dynamikę (bez uwzględnienia drapieżnictwa) populacji $\mathcal{P}$ opisuje równanie logistyczne (2.2), to ostatecznie zmiana liczebności podlega równaniu

$\dot{N}(t)=rN(t)\left(1-\frac{N(t)}{K}\right)-\beta\frac{N(t)}{N_{{1/2}}+N(t)},$

(3.4)

gdzie $\beta=\tfrac{D}{T_{k}}$ oznacza maksymalne drapieżnictwo i $N_{{1/2}}=\tfrac{1}{aT_{k}}$ odpowiada takiej liczebności populacji, przy której drapieżnictwo jest równe połowie maksymalnej wielkości $\beta$ (maksymalną wielkość osiąga się asymptotycznie, przy $N\to\infty$ ).

Postać równania (3.4) nie daje gwarancji znalezienia rozwiązania analitycznego, ale metody portretu fazowego i badania wklęsłości/wypukłości rozwiązań omówione w kontekście poprzednich modeli mogą być zastosowane z powodzeniem także w tym przypadku. Przeanalizowanie dynamiki modelu (3.4) pozostawiamy jako ćwiczenie.

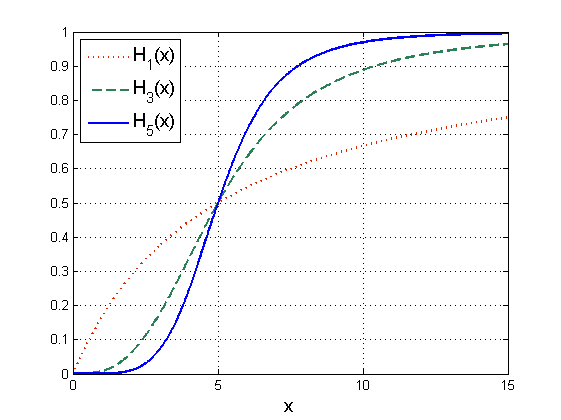
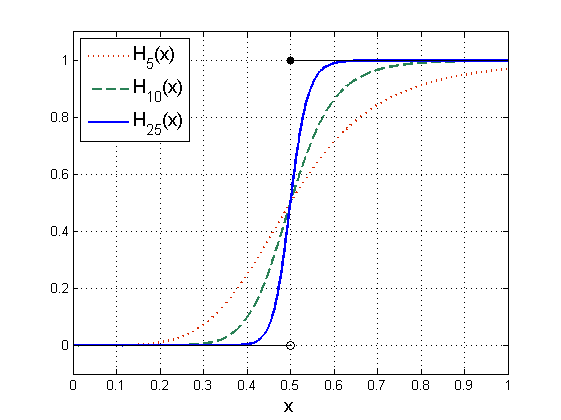
Wyprowadzona powyżej postać odpowiedzi funkcjonalnej (3.3) stanowi szczególny przypadek funkcji Hilla

$H_{{n}}(x)=a\frac{x^{n}}{b^{n}+x^{n}},\quad n>0,$

(3.5)

przy czym stałą $n$ nazywamy współczynnikiem Hilla i w ogólnym przypadku nie musi to być liczba naturalna.

Rys. 3.3. Porównanie wykresu funkcji Hilla dla różnych wartości parametru $n$ przy ustalonych parametrach $a$ i $b$ .

Widzimy, że dla $n=1$ funkcja Hilla odpowiada funkcjonalnej odpowiedzi Hollinga typu II. Funkcja Hilla została zaproponowana do opisu reakcji biochemicznych i w tym przypadku odzwierciedla ona szybkość reakcji. W szczególności $n=2$ opisuje przypadek, gdy w reakcji biorą udział bimery (cząsteczki powstałe z połączenia dwóch pojedynczych monomerów). Zauważmy, że funkcja $H_{n}$ opisuje reakcje, które ulegają wysyceniu, przy czym w zależności od współczynnika $n$ mają różne tempo przebiegu reakcji dla $x$ blisko $0$ i dla dużych $x$ . Im większe $n$ , tym szybsze są zmiany w otoczeniu punktu krytycznego $x_{p}=\sqrt[n]{\frac{n-1}{n+1}}b$ (będącego punktem przegięcia $H_{n}$ ). Funkcje Hilla możemy także interpretować jako gładkie przybliżenie tzw. funkcji przełączeniowych

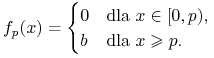$f_{p}(x)=\begin{cases}0&\text{dla}\ x\in[0,p),\\ b&\text{dla}\ x\geq p.\end{cases}$

Wykres ilustrujący jak ze wzrostem $n$ funkcja Hilla z odpowiednimi parametrami $a$ i $b$ coraz lepiej przybliża ustaloną funkcję przełączeniową.

Rys. 3.4. Wykres ilustrujący jak ze wzrostem $n$ funkcja Hilla z odpowiednimi parametrami $a$ i $b$ coraz lepiej przybliża ustaloną funkcję przełączeniową.

Funkcje Hilla są bardzo często wykorzystywane do opisu różnych procesów ulegających wysyceniu — wielkość współczynnika Hilla zależy wtedy od szybkości zmian danego procesu.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Modelowanie matematyczne w biologii i medycynie

Zagadnienia

3. Modelowanie pojedynczej populacji III

3.1. Efekt Alleego

3.2. Funkcjonalna odpowiedź Hollinga i funkcja Hilla