Zagadnienia
4. Modele pojedynczej populacji z uwzględnieniem wieku I
Przejdziemy teraz do opisu sytuacji, gdy populacja nie jest jednorodna — rozróżniamy osobniki w różnym wieku.
4.1. Ciąg Fibonacciego
W najprostszym przypadku w populacji wyodrębniamy dwie grupy wiekowe:
-
osobników niedojrzałych (w wieku przed reprodukcyjnym);
-
osobników dojrzałych (w wieku reprodukcyjnym).
Co ciekawe, model opisujący taką sytuację jest najstarszym znanym modelem populacyjnym i znamy go pod nazwą ciągu Fibonacciego.
W I połowie XIII wieku Leonardo z Pizy (Fibonacci, czyli ,,filus Bonacci” — syn Bonacciego) zastosował ten ciąg do opisu następującego zagadnienia populacyjnego.
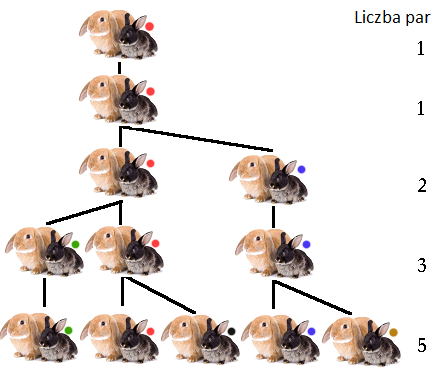
,,Pewien człowiek wziął parę królików i umieścił je w miejscu otoczonym ze wszystkich stron murem. Ile par królików urodzi się z tej pary w ciągu roku, jeśli założymy, że z każdej pary po miesiącu rodzi się nowa para, która staje się płodna po upływie kolejnego miesiąca?”
Liber abaci rozdział III.
Jako rozwiązanie tego zagadnienia Fibonacci zaproponował ciąg:
znany dziś właśnie jako ciąg Fibonacciego. Ogólny wyraz tego ciągu opisujemy za pomocą formuły rekurencyjnej
| (4.1) |
W Liber abaci Fibonacci pominął pierwszy wyraz ciągu — zauważmy, że powinny być dwa wyrazy równe ![]() , gdyż pierwsza para też staje się płodna dopiero po upływie miesiąca, por. rys. 4.1.
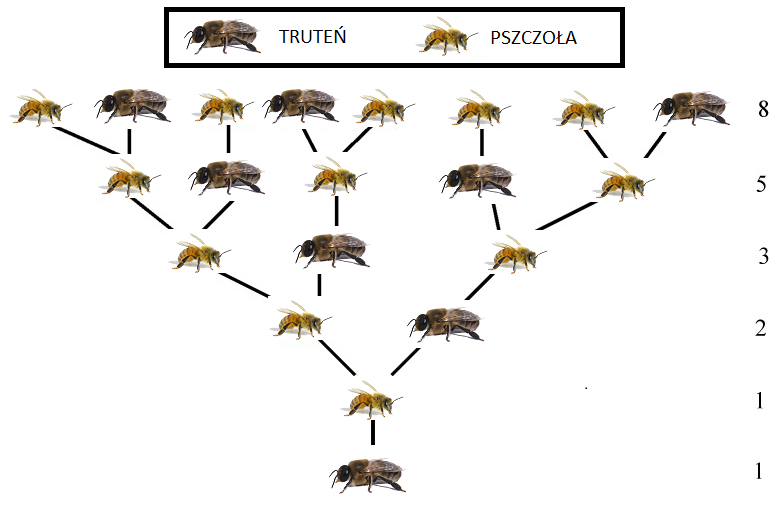
Analogiczny schemat opisuje liczbę przodków pojedynczego trutnia w roju pszczół, por. rys. 4.2.
, gdyż pierwsza para też staje się płodna dopiero po upływie miesiąca, por. rys. 4.1.
Analogiczny schemat opisuje liczbę przodków pojedynczego trutnia w roju pszczół, por. rys. 4.2.
Nazwijmy kolejne wyrazy ciągu Fibonacciego liczbami Fibonacciego. Okazuje się, że liczby Fibonacciego opisują różne wielkości przyrodnicze, jak np. liczbę płatków kwiatów (stokrotki stanowią sztandarowy przykład, typowo liczba płatków równa jest 34, 55 albo 89!), liczbę pędów roślin w kolejnych fazach wzrostu, czy też liczbę spiral w różnych konstrukcjach spiralnych (spirale prawoskrętne i lewoskrętne), takich jak kwiatostany słonecznika, owoc ananasa czy szyszki, por. rys. 4.3.
Równanie (4.1) jest liniowym równaniem dyskretnym, przy czym możemy je traktować jako równanie z opóźnionym argumentem — typowo dyskretny układ dynamiczny bez opóźnienia zapisujemy w postaci
| (4.2) |
gdzie ![]() opisuje liczebność populacji (czy inną wielkość biofizyczną) w chwili
opisuje liczebność populacji (czy inną wielkość biofizyczną) w chwili ![]() , a
, a ![]() odzwierciedla prawa rządzące dynamiką tej populacji. W ogólnym przypadku
odzwierciedla prawa rządzące dynamiką tej populacji. W ogólnym przypadku ![]() . Oczywiście postać funkcji
. Oczywiście postać funkcji ![]() zależy od modelu heurystycznego (np. dla modelu Malthusa (1.3) funkcja
zależy od modelu heurystycznego (np. dla modelu Malthusa (1.3) funkcja ![]() jest liniowa) i w istotny sposób wpływa na przebieg rozwiązań, czyli dynamikę ciągu
jest liniowa) i w istotny sposób wpływa na przebieg rozwiązań, czyli dynamikę ciągu ![]() . Dyskretny układ z opóźnieniem zawsze możemy sprowadzić do układu postaci (4.2) wprowadzając pomocnicze zmienne.
Przyjrzyjmy się tej procedurze na przykładzie ciągu Fibonacciego (4.1).
Niech
. Dyskretny układ z opóźnieniem zawsze możemy sprowadzić do układu postaci (4.2) wprowadzając pomocnicze zmienne.
Przyjrzyjmy się tej procedurze na przykładzie ciągu Fibonacciego (4.1).
Niech ![]() oznacza wektor kolejnych liczebności
oznacza wektor kolejnych liczebności ![]() .
Wtedy
.
Wtedy
zatem jedno równanie z opóźnieniem rzędu jednej jednostki czasu zamienia się na układ dwóch równań postaci (4.2). Liczba równań w układzie wyjściowym zależy od wielkości opóźnień w układzie początkowym.
Jak już przypominaliśmy przy rozwiązywaniu równania (1.3), rozwiązań układu (4.2) dla liniowej funkcji ![]() szukamy w postaci
szukamy w postaci ![]() , gdzie
, gdzie ![]() jest wartością własną macierzy przekształcenia
jest wartością własną macierzy przekształcenia ![]() . Podstawiając taką postać rozwiązania do zależności rekurencyjnej (4.1) otrzymujemy
. Podstawiając taką postać rozwiązania do zależności rekurencyjnej (4.1) otrzymujemy
zatem ![]() spełnia równanie
spełnia równanie
| (4.3) |
czyli równanie charakterystyczne dla macierzy ![]() . Rozwiązując równanie (4.3) dostajemy
. Rozwiązując równanie (4.3) dostajemy
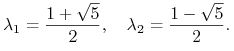 |
Wobec tego wyraz ogólny ciągu Fibonacciego obliczamy jako kombinację liniową
| (4.4) |
gdzie ![]() i
i ![]() musimy wyznaczyć korzystając z warunku początkowego
musimy wyznaczyć korzystając z warunku początkowego ![]() .
Dostajemy zatem układ równań
.
Dostajemy zatem układ równań
![\begin{array}[]{lclcc}a(1+\sqrt{5})&+&b(1-\sqrt{5})&=&2,\\
a{(1+\sqrt{5})^{2}}&+&b{(1-\sqrt{5})^{2}}&=&4,\\
\end{array}](wyklady/mbm/mi/mi329.png) |
skąd obliczamy ![]() i ostatecznie ogólny wyraz ciągu Fibonacciego
i ostatecznie ogólny wyraz ciągu Fibonacciego
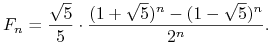 |
(4.5) |
Zauważmy, że ciąg ![]() jest rosnący i
jest rosnący i ![]() przy
przy ![]() . Co więcej, tę samą własność mają wszystkie ciągi określone formułą rekurencyjną (4.1) bez względu na warunek początkowy, o ile tylko
. Co więcej, tę samą własność mają wszystkie ciągi określone formułą rekurencyjną (4.1) bez względu na warunek początkowy, o ile tylko ![]() ,
, ![]() . Jeśli wzór (4.5) przepiszemy w postaci
. Jeśli wzór (4.5) przepiszemy w postaci
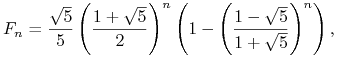 |
to możemy zauważyć, że wraz z rosnącym ![]() dynamika ciągu
dynamika ciągu ![]() jest coraz bliższa dynamice ciągu
jest coraz bliższa dynamice ciągu
![]() determinowanej przez dominującą wartość własną
determinowanej przez dominującą wartość własną ![]() . Wnioskujemy więc, że wraz z rosnącym
. Wnioskujemy więc, że wraz z rosnącym ![]() dynamika ta coraz mniej różni się od dynamiki dyskretnego modelu Malthusa (1.3). Podobne zachowanie zaobserwujemy dla większości wartości początkowych
dynamika ta coraz mniej różni się od dynamiki dyskretnego modelu Malthusa (1.3). Podobne zachowanie zaobserwujemy dla większości wartości początkowych ![]() ,
, ![]() .
.
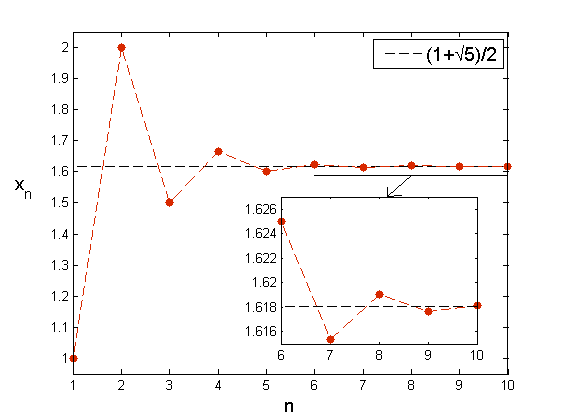
Widzimy więc, że dynamika ciągu Fibonacciego jest raczej ,,uboga”. Spójrzmy jednak na ciąg ![]() . Zdefiniujmy
. Zdefiniujmy
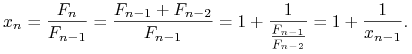 |
Możemy sprawdzić, że ciąg ![]() oscyluje i dzieli się na dwa podciągi
oscyluje i dzieli się na dwa podciągi ![]() ,
, ![]() , monotoniczne, zbieżne do tej samej liczby
, monotoniczne, zbieżne do tej samej liczby ![]() , z czego wynika, że cały ciąg zbiega do tej liczby.
, z czego wynika, że cały ciąg zbiega do tej liczby.
Liczba ta znana jest od starożytności, oznaczamy ją ![]() i definiuje ona tzw. złotą proporcję lub złoty podział. Nazwa ta wiąże się z podziałem odcinka na dwie części, z których dłuższa do krótszej ma się tak jak cały odcinek do dłuższej. W starożytności mówiono także o ,,boskiej proporcji” i wykorzystywano ją w wielu różnych konstrukcjach, także przy budowie Partenonu. Również w czasach nowożytnych wielu ludzi doszukuje się liczb Fibonacciego czy złotej proporcji w różnych zjawiskach, najczęściej jednak nie ma to prawie żadnych podstaw naukowych.
i definiuje ona tzw. złotą proporcję lub złoty podział. Nazwa ta wiąże się z podziałem odcinka na dwie części, z których dłuższa do krótszej ma się tak jak cały odcinek do dłuższej. W starożytności mówiono także o ,,boskiej proporcji” i wykorzystywano ją w wielu różnych konstrukcjach, także przy budowie Partenonu. Również w czasach nowożytnych wielu ludzi doszukuje się liczb Fibonacciego czy złotej proporcji w różnych zjawiskach, najczęściej jednak nie ma to prawie żadnych podstaw naukowych.
4.2. Macierze Lesliego
W ogólnym przypadku możemy wyodrębnić więcej grup wiekowych. Niech populacja ![]() będzie podzielona na
będzie podzielona na ![]() grup wiekowych. W tej sytuacji liczebność całej populacji jest opisana za pomocą wektora
grup wiekowych. W tej sytuacji liczebność całej populacji jest opisana za pomocą wektora ![]() , gdzie
, gdzie ![]() oznacza liczebność grupy wiekowej
oznacza liczebność grupy wiekowej ![]() w chwili
w chwili ![]() , dla
, dla ![]() mamy osobniki nowonarodzone, a dla
mamy osobniki nowonarodzone, a dla ![]() — osobniki najstarsze, które nie mają szansy dożyć do następnej chwili. Podobnie jak w przypadku modelu Malthusa chcemy na podstawie znajomości wektora liczebności
— osobniki najstarsze, które nie mają szansy dożyć do następnej chwili. Podobnie jak w przypadku modelu Malthusa chcemy na podstawie znajomości wektora liczebności ![]() określić
określić ![]() . Jak zwykle musimy zacząć od modelu heurystycznego, czyli omówienia procesów, które są według nas istotne przy opisie dynamiki populacji
. Jak zwykle musimy zacząć od modelu heurystycznego, czyli omówienia procesów, które są według nas istotne przy opisie dynamiki populacji ![]() . Ponownie podobnie jak w modelu Malthusa zakładamy, że osobniki są jednorodne w obrębie każdej grupy wiekowej, w każdej grupie wiekowej mamy do czynienia tylko z dwoma procesami — rozrodczości i starzenia się/śmiertelności, przy czym współczynniki rozrodczości i starzenia się są charakterystyczne dla danej grupy wiekowej. Analogicznie jak w przypadku modelu Malthusa w obrębie danej grupy wiekowej oba procesy przebiegają tak samo dla wszystkich osobników i są rozłożone równomiernie w czasie. Zakładamy też, że jednostka czasu jest równa jednostce zmiany wieku (starzenia się), czyli że po upływie np. jednego roku osobnik starzeje się o rok, co więcej po upływie jednej jednostki czasu przechodzi do następnej grupy wiekowej albo umiera.
Dostajemy więc:
. Ponownie podobnie jak w modelu Malthusa zakładamy, że osobniki są jednorodne w obrębie każdej grupy wiekowej, w każdej grupie wiekowej mamy do czynienia tylko z dwoma procesami — rozrodczości i starzenia się/śmiertelności, przy czym współczynniki rozrodczości i starzenia się są charakterystyczne dla danej grupy wiekowej. Analogicznie jak w przypadku modelu Malthusa w obrębie danej grupy wiekowej oba procesy przebiegają tak samo dla wszystkich osobników i są rozłożone równomiernie w czasie. Zakładamy też, że jednostka czasu jest równa jednostce zmiany wieku (starzenia się), czyli że po upływie np. jednego roku osobnik starzeje się o rok, co więcej po upływie jednej jednostki czasu przechodzi do następnej grupy wiekowej albo umiera.
Dostajemy więc:
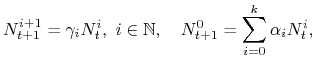 |
gdzie ![]() odzwierciedla przeżywalność osobników z grupy wiekowej
odzwierciedla przeżywalność osobników z grupy wiekowej ![]() (zatem
(zatem ![]() to śmiertelność), a
to śmiertelność), a ![]() — rozrodczość danej grupy wiekowej. W związku z tym formalnie model Lesliego można przedstawić jako trójkę
— rozrodczość danej grupy wiekowej. W związku z tym formalnie model Lesliego można przedstawić jako trójkę ![]() , gdzie wektory
, gdzie wektory ![]() ,
, ![]() ,
, ![]() oznaczają odpowiednio liczebności początkowe, współczynniki rozrodczości oraz śmiertelności,
oznaczają odpowiednio liczebności początkowe, współczynniki rozrodczości oraz śmiertelności, ![]() .
.
Zapisując ten model w postaci (4.2) otrzymujemy
| (4.6) |
gdzie
![\mathbf{M}=\left(\begin{array}[]{ccccc}\alpha _{0}&\alpha _{1}&\alpha _{2}&\ldots&\alpha _{k}\\
\gamma _{0}&0&0&\ldots&0\\
0&\gamma _{1}&0&\ldots&0\\
\vdots&0&\ddots&\ddots&\vdots\\
0&\ldots&\ldots&\gamma _{{k-1}}&0\end{array}\right),](wyklady/mbm/mi/mi326.png) |
przy czym macierz ![]() nazywamy macierzą Lesliego, a model (4.6) modelem (macierzowym) Lesliego (patrz [8, 9, 2]). Jeśli mamy zadany początkowy rozkład wieku
nazywamy macierzą Lesliego, a model (4.6) modelem (macierzowym) Lesliego (patrz [8, 9, 2]). Jeśli mamy zadany początkowy rozkład wieku ![]() , to rozkład w dowolnej chwili
, to rozkład w dowolnej chwili ![]() możemy obliczyć ze wzoru
możemy obliczyć ze wzoru
Dla dowolnych ![]() ,
, ![]() zachodzi też
zachodzi też ![]() .
.
Definicja 4.1
Stanem równowagi modelu Lesliego nazwiemy parę ![]() spełniającą zależność
spełniającą zależność
gdzie ![]() jest wektorem liczebności, który nazywamy ustaloną strukturą wieku, a
jest wektorem liczebności, który nazywamy ustaloną strukturą wieku, a ![]() oznacza stały współczynnik wzrostu.
oznacza stały współczynnik wzrostu.
W przypadku macierzy Lesliego liniowa niezależność wierszy i kolumn pozwala zapisać ![]() w postaci
w postaci
gdzie ![]() to diagonalna macierz wartości własnych, a
to diagonalna macierz wartości własnych, a ![]() macierz kolumnowych wektorów własnych
macierz kolumnowych wektorów własnych ![]() .
Wynika stąd, że
.
Wynika stąd, że
Oznaczmy ![]() ,
, ![]() . Wtedy
. Wtedy
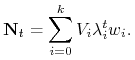 |
(4.7) |
Własności rozwiązań zależą zarówno od postaci macierzy ![]() jak i początkowego rozkładu wieku. Twierdzenie Frobeniusa – Perrona gwarantuje istnienie dominującej rzeczywistej wartości własnej
jak i początkowego rozkładu wieku. Twierdzenie Frobeniusa – Perrona gwarantuje istnienie dominującej rzeczywistej wartości własnej ![]() ,
, ![]() . Dla tej wartości własnej zarówno prawo jak i lewostronny wektor własny jest rzeczywisty i ma nieujemne współrzędne. Jeśli macierz
. Dla tej wartości własnej zarówno prawo jak i lewostronny wektor własny jest rzeczywisty i ma nieujemne współrzędne. Jeśli macierz ![]() spełnia pewne dodatkowe założenia, np. gdy wskaźniki
spełnia pewne dodatkowe założenia, np. gdy wskaźniki ![]() , dla których
, dla których ![]() nie mają większego wspólnego dzielnika niż
nie mają większego wspólnego dzielnika niż ![]() , to
, to ![]() ,
, ![]() i odpowiadający jej wektor własny
i odpowiadający jej wektor własny
![]() ma współrzędne nieujemne i dla większości warunków początkowych asymptotyczne zachowanie rozwiązań jest determinowane przez
ma współrzędne nieujemne i dla większości warunków początkowych asymptotyczne zachowanie rozwiązań jest determinowane przez ![]() , gdzie
, gdzie ![]() jest stałą zależną od warunku początkowego, ponieważ ze wzoru (4.7) dla dominującej wartości własnej
jest stałą zależną od warunku początkowego, ponieważ ze wzoru (4.7) dla dominującej wartości własnej ![]() wynika rozkład asymptotyczny
wynika rozkład asymptotyczny
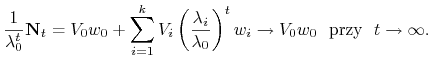 |
Wobec tego dla większości warunków początkowych populacja asymptotycznie osiąga rozkład wieku ![]() przy współczynniku rozrodczości
przy współczynniku rozrodczości ![]() , gdyż
, gdyż
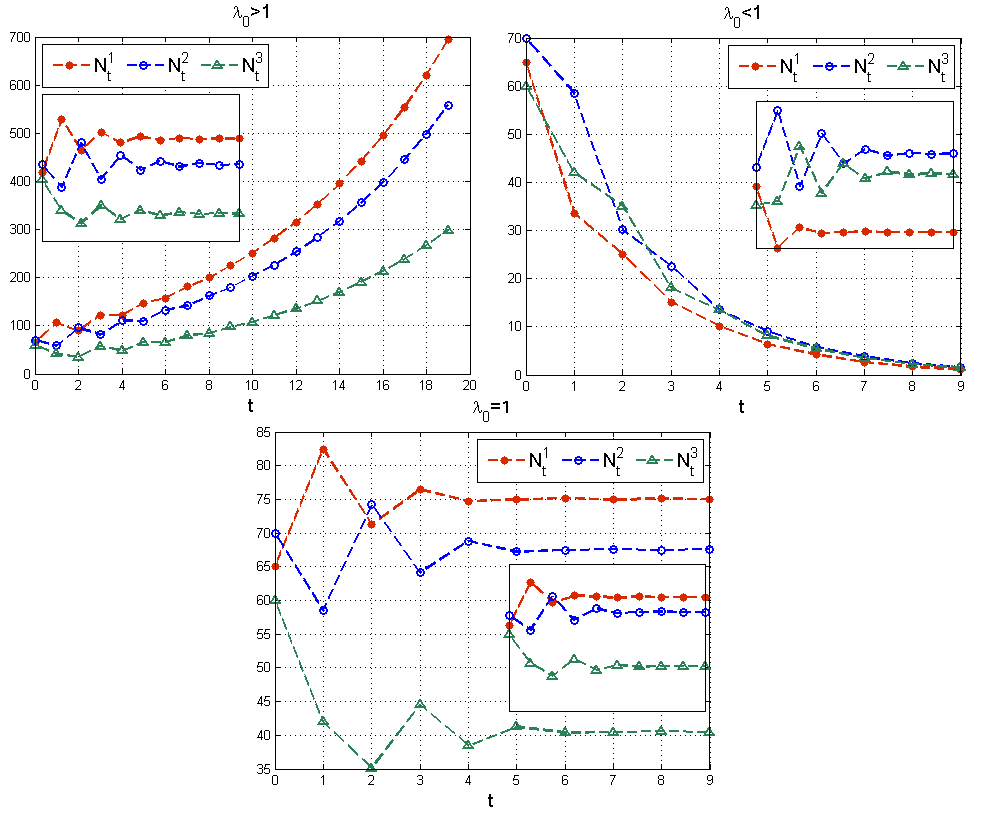
i jeśli
-
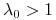 , to liczebności wszystkich grup wiekowych rosną nieograniczenie, mówimy że populacja jest rozwojowa;
, to liczebności wszystkich grup wiekowych rosną nieograniczenie, mówimy że populacja jest rozwojowa; -
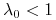 , to populacja jest wymierająca;
, to populacja jest wymierająca; -
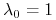 , to liczebność całej populacji i poszczególnych grup wiekowych stabilizuje się — populacja jest stacjonarna, por rys. 4.5.
, to liczebność całej populacji i poszczególnych grup wiekowych stabilizuje się — populacja jest stacjonarna, por rys. 4.5.
Wektor ![]() odzwierciedla rozkład liczebności populacji w stanie równowagi, przy czym jeśli
odzwierciedla rozkład liczebności populacji w stanie równowagi, przy czym jeśli ![]() , to współrzędne tego wektora odzwierciedlają procentowy wkład poszczególnych grup wiekowych w populację.
W takiej sytuacji dynamika modelu Lesliego jest podobna do dynamiki modelu Malthusa, co więcej, jeśli rozpatrzymy całkowitą liczebność populacji
, to współrzędne tego wektora odzwierciedlają procentowy wkład poszczególnych grup wiekowych w populację.
W takiej sytuacji dynamika modelu Lesliego jest podobna do dynamiki modelu Malthusa, co więcej, jeśli rozpatrzymy całkowitą liczebność populacji 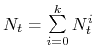 , to
, to ![]() .
.
Możliwe jest jednak także inne zachowanie rozwiązań, w szczególności cykliczne zmiany struktury wieku.
Wiąże się to między innymi z dynamiką determinowaną przez początkowe rozkłady wieku należące do podprzestrzeni generowanych przez wektory własne odpowiadające wartościom własnym ![]() w sytuacji, gdy wśród tych wartości własnych nie ma już kolejnej dominującej. Oczywiście zależy to w istotny sposób od postaci macierzy Lesliego.
Rozpatrzmy przykład macierzy Lesliego odzwierciedlającej sytuację, gdy rozmnażają się tylko osobniki najstarsze. Rozpatrzmy przykład populacji z wydzielonymi dwoma grupami wiekowymi — rozróżniamy osobniki dojrzałe, zdolne do reprodukcji i osobniki niedojrzałe. Mamy więc
w sytuacji, gdy wśród tych wartości własnych nie ma już kolejnej dominującej. Oczywiście zależy to w istotny sposób od postaci macierzy Lesliego.
Rozpatrzmy przykład macierzy Lesliego odzwierciedlającej sytuację, gdy rozmnażają się tylko osobniki najstarsze. Rozpatrzmy przykład populacji z wydzielonymi dwoma grupami wiekowymi — rozróżniamy osobniki dojrzałe, zdolne do reprodukcji i osobniki niedojrzałe. Mamy więc
| (4.8) |
Obliczając kolejne potęgi macierzy (4.6) dostajemy
co łatwo wykazać indukcyjnie.
Zauważmy, że jeśli ![]() i
i ![]() , to
, to ![]() oraz
oraz
![]() , czyli mamy zachowanie cykliczne, por. rys. 4.6.
, czyli mamy zachowanie cykliczne, por. rys. 4.6.