Zagadnienia

5.1 Modele z opóźnieniem

5. Modele pojedynczej populacji z uwzględnieniem wieku II

5.1. Modele z opóźnieniem

Innym sposobem wprowadzenia pewnej zależności od wieku jest modelowanie przy użyciu równań z opóźnieniem. Wróćmy do opisu dynamiki populacji za pomocą wzoru (2.1) i załóżmy, że przyrost per capita zależy nie od liczebności populacji w bieżącej chwili $t$ , ale od stanu w pewnej chwili w przeszłości $t-\tau$ . Kiedy tak się będzie działo? Wyobraźmy sobie populację roślinożerców, które zjadają rośliny będące w pewnym konkretnym wieku $\tau$ i jest to jednocześnie wiek, w którym te rośliny rozsiewają nasiona. Jeśli roślina zostanie zjedzona, to nie rozsieje nasion, a wtedy w przyszłości osobniki opisywanej populacji nie mają co jeść. Ilość zjedzonych roślin zależy od stanu populacji w bieżącej chwili, zatem ilość jedzenia w przyszłości, czyli przyrost per capita, zależy od tego stanu. Przy takich założeniach równanie na przyrost per capita przyjmuje postać

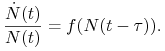$\frac{\dot{N}(t)}{N(t)}=f(N(t-\tau)).$

W szczególności równanie logistyczne z opóźnieniem zaproponowane przez G. E. Hutchinsona w 1948 r. zapiszemy jako

$\dot{N}(t)=rN(t)\left(1-\frac{N(t-\tau)}{K}\right).$

(5.1)

Oczywiste jest, że przy opisanym powyżej modelu heurystycznym powinniśmy rozważać nie dokładnie jedno ustalone opóźnienie $\tau$ , ale pewien rozkład opóźnienia, gdyż nie ma w naturze takich roślin, które rozsiewałyby nasiona dokładnie w danym wieku, ale jak zwykle staraliśmy się zbudować jak najprostszy model, zatem przyjęliśmy uproszczenie polegające na ustaleniu opóźnienia $\tau$ .

Chcemy zbadać zależność rozwiązań równania (5.1) od wielkości opóźnienia $\tau>0$ . Zajmiemy się najpierw omówieniem podstawowych własności, takich jak istnienie, jednoznaczność i nieujemność rozwiązań dla nieujemnego warunku początkowego. Zauważmy, że aby rozwiązać równanie z opóźnieniem $\tau$ nie wystarczy, że określimy początkową liczebność populacji $N(0)=N_{0}$ , ale musimy zadać funkcję początkową określoną na przedziale długości opóźnienia, czyli $N_{0}:[-\tau,0]\to\mathbb{R}^{+}$ . Typowo w teorii równań różniczkowych z opóźnionym argumentem zakładamy, że funkcja początkowa jest ciągła, ale nie zawsze jest to założenie konieczne. W szczególności — znając funkcję początkową $N_{0}$ możemy rozwiązać równanie (5.1) metodą kroków, o ile tylko funkcja początkowa jest całkowalna. Dokładniej, niech $t\in[0,\tau]$ . Wtedy

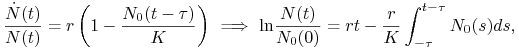$\frac{\dot{N}(t)}{N(t)}=r\left(1-\frac{N_{0}(t-\tau)}{K}\right)\ \Longrightarrow\ \text{ln}\frac{N(t)}{N_{0}(0)}=rt-\frac{r}{K}\int _{{-\tau}}^{{t-\tau}}N_{0}(s)ds,$

czyli

$N(t)=N_{0}(0)\text{exp}\left(rt-\frac{r}{K}\int _{{-\tau}}^{{t-\tau}}N_{0}(s)ds\right)\quad\text{dla}\quad t\in[0,\tau].$

Oznaczmy otrzymane rozwiązanie przez $N_{1}(t)=N_{0}(0)\exp\left(rt-\frac{r}{K}\int _{{-\tau}}^{{t-\tau}}N_{0}(s)ds\right)$ dla $t\in[0,\tau]$ . Zauważmy, że jest ono dobrze określone dla ciągłej funkcji początkowej, co więcej w tym przypadku wystarczy, żeby funkcja $N_{0}$ była całkowalna. Mamy też jednoznaczność, a nieujemność wynika z nierówności $N_{0}(0)\geq 0$ , przy czym $N_{0}(0)=0$ implikuje $N(t)\equiv 0$ (stany stacjonarne równań z opóźnieniem są oczywiście takie same jak dla analogicznego równania bez opóźnienia, skoro nie zależą one od czasu). Teraz zastosujemy metodę indukcji matematycznej. Załóżmy, że znamy rozwiązanie $N_{k}(t)$ na przedziale $[(k-1)\tau,k\tau]$ i znajdźmy rozwiązanie na kolejnym przedziale

$N_{{k+1}}(t)=N_{k}(k\tau)\text{exp}\left(r(t-k\tau)-\frac{r}{K}\int _{{(k-1)\tau}}^{{t-\tau}}N_{k}(s)ds\right)\quad\text{dla}\quad t\in[k\tau,(k+1)\tau].$

Wobec tego metoda indukcji matematycznej gwarantuje, że rozwiązanie istnieje dla dowolnego $t\geq 0$ i ma pożądane własności.

Zbadamy teraz własności asymptotyczne rozwiązań, w szczególności stabilność lokalną rozwiązań stacjonarnych. Metoda badania stabilności jest analogiczna, jak stosowana w przypadku równań bez opóźnienia. Przeprowadzamy najpierw linearyzację wokół stanu stacjonarnego. Niech $\bar{N}$ będzie rozwiązaniem stacjonarnym, czyli $\bar{N}=0$ albo $\bar{N}=K$ . Wprowadzamy nową zmienną $x(t)$ , która oznacza odchylenie od stanu stacjonarnego, $N(t)=\bar{N}+x(t)$ , przy czym zakładamy, że $|x(t)|<\varepsilon$ i pomijamy wyrazy rzędu $\varepsilon^{2}$ . Mamy

$\dot{x}(t)=r(\bar{N}+x(t))\left(1-\frac{\bar{N}+x(t-\tau)}{K}\right)\approx rx(t)\left(1-\frac{\bar{N}}{K}\right)-r\bar{N}\frac{x(t-\tau)}{K}$

po pominięciu składnika $-rx(t)\tfrac{x(t-\tau)}{K}$ i zauważeniu, że $r\bar{N}\left(1-\tfrac{\bar{N}}{K}\right)=0$ dla obu stanów stacjonarnych.

Dla stanu stacjonarnego $\bar{N}=0$ równanie zlinearyzowane ma postać

$\dot{x}(t)=rx(t).$

Widzimy więc, że odchylenie od stanu stacjonarnego $x(t)$ rośnie, zatem $\bar{N}=0$ jest niestabilne.

Z kolei dla dodatniego stanu stacjonarnego

$\dot{x}(t)=-rx(t-\tau).$

Jak zbadać stabilność stanu stacjonarnego $\bar{x}=0$ powyższego równania? Tak jak w przypadku równań bez opóźnienia szukamy rozwiązań w postaci wykładniczej $x(t)=x_{0}\text{e}^{{\lambda t}}$ . Jeśli wszystkie wartości własne $\lambda$ mają części rzeczywiste ujemne, to $x(t)\to 0$ przy $t\to+\infty$ dla dostatecznie małych $x_{0}$ . Stąd odchylenie maleje do $0$ , zatem stan $\bar{N}=K$ równania (5.1) jest lokalnie asymptotycznie stabilny. Jeśli natomiast istnieje wartość własna o części rzeczywistej dodatniej, to $\bar{N}=K$ jest niestabilny. Okazuje się, że dla równań z opóźnieniem równanie charakterystyczne, w tym przypadku

$\lambda=-r\text{e}^{{-\lambda\tau}},$

ma nieskończenie wiele rozwiązań, które zależą w sposób ciągły od parametrów, w szczególności od opóźnienia. Skoro dla $\tau=0$ mamy $\lambda=-r<0$ , to dla małych opóźnień stan $\bar{N}=K$ pozostaje stabilny. Zastanówmy się kiedy może nastąpić destabilizacja. Skoro niestabilność wiąże się z pojawieniem się wartości własnej o dodatniej części rzeczywistej, to dla pewnej krytycznej wartości $\tau^{k}>0$ musimy mieć $\lambda=\pm i\omega$ , $\omega>0$ , i wartości własne przechodzą z lewej półpłaszczyzny zespolonej na prawą, więc $\frac{d\Re(\lambda)}{d\tau}\Big|_{{\tau=\tau^{k}}}>0$ , gdzie $\Re(\lambda)$ oznacza część rzeczywistą wartości własnej, por. rys. 5.1.

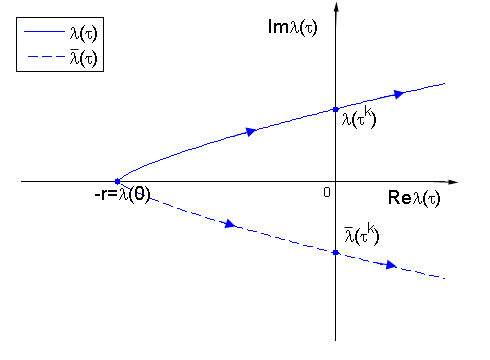
Poglądowa ilustracja destabilizacji stanu stacjonarnego poprzez przejście wartości własnych z lewej półpłaszczyzny zespolonej na prawą.

Rys. 5.1. Poglądowa ilustracja destabilizacji stanu stacjonarnego poprzez przejście wartości własnych z lewej półpłaszczyzny zespolonej na prawą.

Jeśli $\lambda=\pm i\omega$ , to

$\pm i\omega=-r\text{e}^{{\mp i\omega\tau^{k}}}\Rightarrow|i\omega|=|r\text{e}^{{\mp i\omega\tau^{k}}}|,$

ale $|\text{e}^{{\mp i\omega\tau^{k}}}|=1$ , więc $\omega _{k}=r$ (w ogólnym przypadku łatwiej rozpatrywać tę równość po podniesieniu do kwadratu). Znając krytyczną wartość własną obliczamy $\tau^{k}$

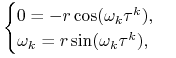$\begin{cases}0=-r\cos(\omega _{k}\tau^{k}),\\ \omega _{k}=r\sin(\omega _{k}\tau^{k}),\end{cases}$

czyli $\cos(\omega _{k}\tau^{k})=0$ i $\sin(\omega _{k}\tau^{k})=1$ , wobec tego $\omega _{k}\tau^{k}=\tfrac{\pi}{2}+2n\pi$ , $n\in\mathbb{N}$ . Mamy więc ciąg krytycznych wartości własnych $\left(\tau^{k}_{n}\right)_{{n=0}}^{{\infty}}$ . Okazuje się, że znak $\frac{d\Re(\lambda)}{d\tau}\Big|_{{\tau=\tau^{k}}}$ możemy sprawdzić korzystając z już przeprowadzonych obliczeń. W ogólnym przypadku dla układu równań z pojedynczym opóźnieniem $\tau$ równanie charakterystyczne ma postać

$P(\lambda)+Q(\lambda)\text{e}^{{-i\lambda\tau}}=0$

i dla czysto urojonych wartości własnych $\lambda=i\omega$ , $\omega>0$ , definiujemy funkcję pomocniczą

$F(\omega)=||P(i\omega)||^{2}-||Q(i\omega)||^{2},$

której miejsca zerowe wyznaczają czysto urojone wartości własne. U nas $F(\omega)=\omega^{2}-r^{2}$ . Podstawiamy $y=\omega^{2}$ i rozpatrujemy $\tilde{F}(y)=y-r^{2}$ . Pochodna tej funkcji w punkcie $y=\omega _{k}^{2}$ ma taki sam znak jak $\frac{d\Re(\lambda)}{d\tau}\Big|_{{\tau=\tau^{k}}}$ . W naszym przypadku $\tilde{F}^{{\prime}}(y)=1>0$ , zatem zawsze wartości własne przechodzą z lewej półpłaszczyzny na prawą. Wobec tego dla pierwszej wartości krytycznej $\tau^{k}_{0}=\tfrac{\pi}{2r}$ następuje destabilizacja i rozwiązanie $\bar{N}=K$ pozostaje niestabilne dla wszystkich $\tau>\tau^{k}_{0}$ . Ten mechanizm destabilizacji nazywamy bifurkacją Hopfa. W jej wyniku pojawiają się nietrywialne rozwiązania okresowe o okresie $\tfrac{2\pi}{\omega _{k}}=\tfrac{2\pi}{r}$ , co widzimy na wykresach na rys. 5.2.

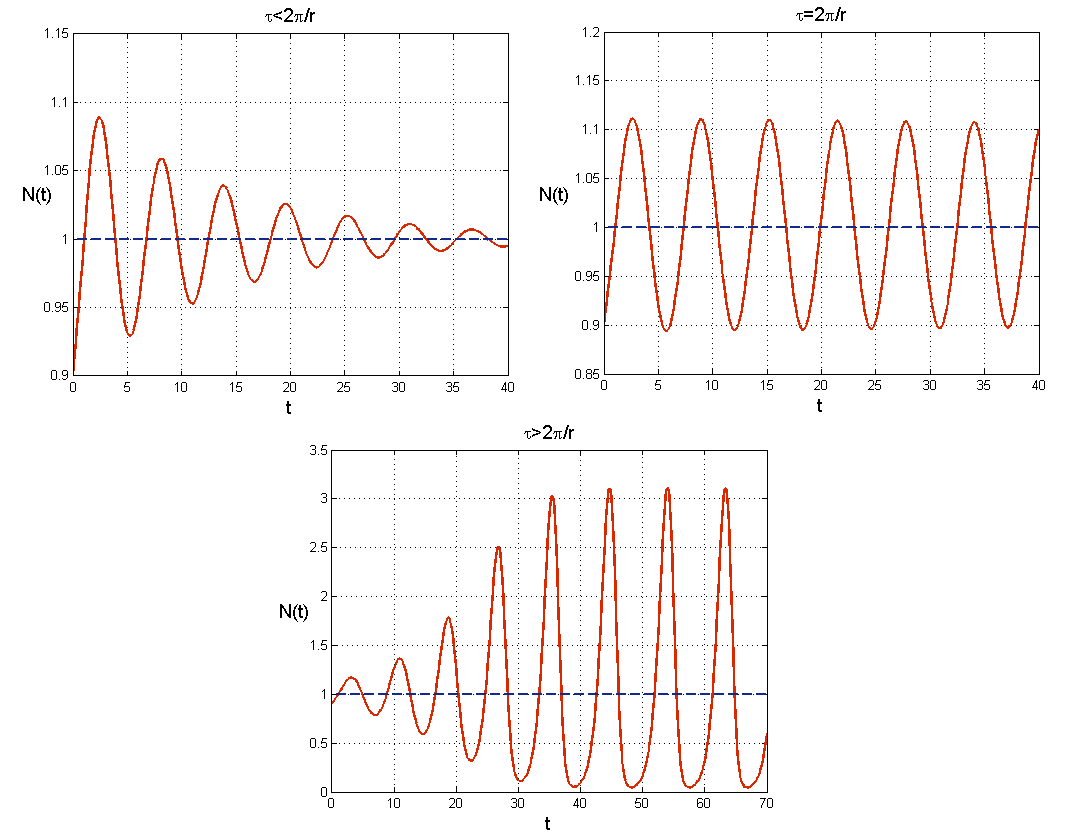
$Wykresy przedstawiające rozwiązania równania~\eqref{log-op} dla różnych wartości opóźnienia $\tau\,.$$

Rys. 5.2. Wykresy przedstawiające rozwiązania równania (5.1) dla różnych wartości opóźnienia $\tau$ . Odpowiednio od lewej: $\tau<\tau^{k}_{0}$ ; $\tau=\tau^{k}_{0}$ ; $\tau>\tau^{k}_{0}$ .

Podsumowując tę tematykę należy stwierdzić, że wprowadzenie do opisu heurystycznego zależności od wieku prowadzi najczęściej do dynamiki oscylacyjnej, która jest zwykle obserwowana w przypadku populacji występujących w naturze. Widzimy też, że opis dynamiki za pomocą równań z opóźnieniem może przypominać zachowanie rozwiązań modeli dyskretnych, gdzie też obserwujemy oscylacje. Co więcej, jeśli prawa strona równania z opóźnieniem reprezentuje np. funkcję Hilla, to dla odpowiednio dużych wartości współczynnika Hilla występują zachowania chaotyczne, znów analogicznie jak w modelach dyskretnych. Możemy przypuszczać, że podobieństwa te wiążą się z podobną strukturą obu typów modeli — w modelach dyskretnych tak jak w równaniach z opóźnieniem dynamika w chwili bieżącej $t$ zależy od stanu układu z chwili poprzedniej $t-1$ .

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Modelowanie matematyczne w biologii i medycynie

Zagadnienia

5. Modele pojedynczej populacji z uwzględnieniem wieku II

5.1. Modele z opóźnieniem