Zagadnienia
7. Modele oddziaływań między dwiema populacjami II
7.1. Model drapieżnik – ofiara z ograniczoną pojemnością środowiska dla ofiar
Jak już wspomnieliśmy, w modelu Lotki – Volterry zostały pominięte różne istotne czynniki, gdyż w zamyśle Volterry taki model powinien być możliwie najprostszy. W szczególności wewnętrzna dynamika populacji ofiar została zbudowana w oparciu o model Malthusa zakładający nieograniczoność pojemności środowiska dla tego gatunku, co przy niewielkiej liczebności drapieżników prowadzi do gwałtownego wzrostu populacji ofiar i przyczynia się do okresowości rozwiązań. Załóżmy więc, że wewnętrzna dynamika gatunku ![]() rządzi się innymi prawami, w szczególności liczebność tej populacji jest ograniczona przez pojemność środowiska. Najprostszym znanym nam modelem opisującym taką dynamikę jest równanie logistyczne, zbudujmy zatem model drapieżnik – ofiara w oparciu o to równanie. Wobec tego, przy oznaczeniach wprowadzonych w wyjściowym modelu Lotki – Volterry, model z ograniczoną pojemnością środowiska dla ofiar możemy opisać następującym układem równań
rządzi się innymi prawami, w szczególności liczebność tej populacji jest ograniczona przez pojemność środowiska. Najprostszym znanym nam modelem opisującym taką dynamikę jest równanie logistyczne, zbudujmy zatem model drapieżnik – ofiara w oparciu o to równanie. Wobec tego, przy oznaczeniach wprowadzonych w wyjściowym modelu Lotki – Volterry, model z ograniczoną pojemnością środowiska dla ofiar możemy opisać następującym układem równań
![\begin{array}[]{ccl}\dot{V}&=&rV\left(1-\frac{V}{K}\right)-aVP,\\
\dot{P}&=&-sP+abVP,\end{array}](wyklady/mbm/mi/mi519.png) |
(7.1) |
gdzie ![]() oznacza pojemność środowiska, analogicznie jak w modelu logistycznym. Dynamika rozwiązań układu (7.1) zależy w istotny sposób od tego parametru. Zauważmy, że postawowe własności takie jak istnienie, jednoznaczność, nieujemność i przedłużalność rozwiązań możemy zbadać w analogiczny sposób jak dla układu (6.1). Wnioskujemy zatem, że dla dowolnego nieujemnego warunku początkowego
oznacza pojemność środowiska, analogicznie jak w modelu logistycznym. Dynamika rozwiązań układu (7.1) zależy w istotny sposób od tego parametru. Zauważmy, że postawowe własności takie jak istnienie, jednoznaczność, nieujemność i przedłużalność rozwiązań możemy zbadać w analogiczny sposób jak dla układu (6.1). Wnioskujemy zatem, że dla dowolnego nieujemnego warunku początkowego ![]() istnieje jednoznaczne, nieujemne rozwiązanie układu (7.1) określone dla wszystkich
istnieje jednoznaczne, nieujemne rozwiązanie układu (7.1) określone dla wszystkich ![]() .
Dość prosto możemy wykazać też ograniczoność rozwiązań. Sformułujmy odpowiednie stwierdzenie
.
Dość prosto możemy wykazać też ograniczoność rozwiązań. Sformułujmy odpowiednie stwierdzenie
Stwierdzenie 7.1
Rozwiązania układu (7.1) dla nieujemnego warunku początkowego ![]() ,
, ![]() ,
, ![]() , pozostają ograniczone. Co więcej,
, pozostają ograniczone. Co więcej, ![]() dla
dla ![]() .
.
Z nieujemności rozwiązań układu (7.1) wynika następujące szacowanie
![]() .
Rzeczywiście, jeśli
.
Rzeczywiście, jeśli ![]() , to
, to ![]() , jak dla równania logistycznego, a jeśli
, jak dla równania logistycznego, a jeśli ![]() , to
, to ![]() i
i ![]() spełnia równanie logistyczne, stąd
spełnia równanie logistyczne, stąd ![]() . Dla
. Dla ![]() ,
, ![]() mamy
mamy ![]() ,
, ![]() dla dowolnego
dla dowolnego ![]() . Rozważmy równanie logistyczne
. Rozważmy równanie logistyczne ![]() z warunkiem początkowym
z warunkiem początkowym ![]() oraz różnicę
oraz różnicę ![]() . Zauważmy, że
. Zauważmy, że
![]() . Zatem na pewnym odcinku
. Zatem na pewnym odcinku ![]() zachodzi
zachodzi ![]() . Jeśli istnieje
. Jeśli istnieje ![]() , takie że
, takie że ![]() , to istnieje pierwsza taka chwila
, to istnieje pierwsza taka chwila ![]() , że
, że ![]() oraz
oraz ![]() , ale
, ale ![]() , co jest sprzeczne z definicją punktu
, co jest sprzeczne z definicją punktu ![]() .
Wynika stąd, że zmienna
.
Wynika stąd, że zmienna ![]() nie przekracza rozwiązań równania logistycznego z warunkiem początkowym
nie przekracza rozwiązań równania logistycznego z warunkiem początkowym ![]() . Zatem
. Zatem ![]() . Załóżmy teraz, że zmienna
. Załóżmy teraz, że zmienna ![]() rośnie nieograniczenie. Mamy wtedy asymptotycznie
rośnie nieograniczenie. Mamy wtedy asymptotycznie ![]() , gdzie stałe
, gdzie stałe ![]() ,
, ![]() zależą od parametrów i warunku początkowego. Stąd
zależą od parametrów i warunku początkowego. Stąd ![]() przy
przy ![]() , co przeczy ograniczoności
, co przeczy ograniczoności ![]() . Zatem zmienna
. Zatem zmienna ![]() także pozostaje ograniczona.
także pozostaje ograniczona.
Zajmiemy się teraz analizą portretu fazowego. Izokliny zerowe są następującymi prostymi
-
dla zmiennej
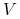 :
: 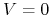 lub
lub 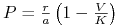 ;
; -
dla zmiennej
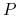 :
: 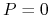 lub
lub 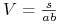 .
.
W zależności od parametru ![]() — nietrywialne izokliny mogą się przeciąć w analizowanej przestrzeni fazowej, gdy
— nietrywialne izokliny mogą się przeciąć w analizowanej przestrzeni fazowej, gdy ![]() jest relatywnie duże, albo nie, gdy
jest relatywnie duże, albo nie, gdy ![]() jest małe. Zatem liczba stanów stacjonarnych zależy od
jest małe. Zatem liczba stanów stacjonarnych zależy od ![]() : zawsze są 2 stany
: zawsze są 2 stany ![]() i
i ![]() , natomiast dla
, natomiast dla ![]() istnieje dodatni stan stacjonarny
istnieje dodatni stan stacjonarny ![]() , gdzie
, gdzie ![]() i
i ![]() . Wyznaczmy wartości własne dla poszczególnych stanów stacjonarnych. Macierz Jacobiego układu (7.1) ma postać
. Wyznaczmy wartości własne dla poszczególnych stanów stacjonarnych. Macierz Jacobiego układu (7.1) ma postać
Stąd wyznaczamy wartości własne
-
dla
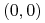 mamy
mamy 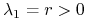 ,
, 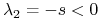 ;
; -
dla
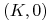 :
: 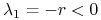 ,
, 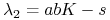 ;
; -
dla
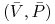 wartości własne są rozwiązaniem równania charakterystycznego
wartości własne są rozwiązaniem równania charakterystycznego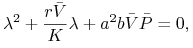
więc w zależności od parametrów albo
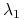 i
i 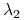 są rzeczywiste ujemne, albo są zespolone i mają ujemne części rzeczywiste.
są rzeczywiste ujemne, albo są zespolone i mają ujemne części rzeczywiste.
Wobec tego stan stacjonarny ![]() jest siodłem bez względu na parametry układu, z kolei
jest siodłem bez względu na parametry układu, z kolei ![]() jest albo węzłem stabilnym, o ile
jest albo węzłem stabilnym, o ile ![]() , czyli dodatni stan stacjonarny nie istnieje, albo siodłem, gdy
, czyli dodatni stan stacjonarny nie istnieje, albo siodłem, gdy ![]() , a wtedy istnieje
, a wtedy istnieje ![]() , który jest albo węzłem, albo ogniskiem stabilnym. Typ punktu krytycznego
, który jest albo węzłem, albo ogniskiem stabilnym. Typ punktu krytycznego ![]() zależy także od
zależy także od ![]() , jeśli
, jeśli ![]() jest duże, tak że
jest duże, tak że ![]() , to obserwujemy ognisko i gasnące oscylacje, w przeciwnym przypadku — węzeł
i zbieżność do stanu stacjonarnego jest od pewnego momentu monotoniczna.
, to obserwujemy ognisko i gasnące oscylacje, w przeciwnym przypadku — węzeł
i zbieżność do stanu stacjonarnego jest od pewnego momentu monotoniczna.
Przystępując do narysowania portretu fazowego zauważmy, że trywialne izokliny zerowe stanowią trajektorie układu. Rzeczywiście: jeśli ![]() ,
, ![]() , jest warunkiem początkowym, to oczywiście
, jest warunkiem początkowym, to oczywiście ![]() , czyli zmienna
, czyli zmienna ![]() nie zmienia się,
nie zmienia się, ![]() dla
dla ![]() , natomiast dla zmiennej
, natomiast dla zmiennej ![]() mamy równanie
mamy równanie ![]() , czyli
, czyli ![]() dla
dla ![]() . Podobnie dla warunku początkowego
. Podobnie dla warunku początkowego ![]() ,
, ![]() , zachodzi
, zachodzi ![]() , czyli
, czyli ![]() dla
dla ![]() oraz
oraz ![]() , zatem
, zatem ![]() spełnia równanie logistyczne, co zauważyliśmy już wcześniej w dowodzie stwierdzenia 7.1.
spełnia równanie logistyczne, co zauważyliśmy już wcześniej w dowodzie stwierdzenia 7.1.
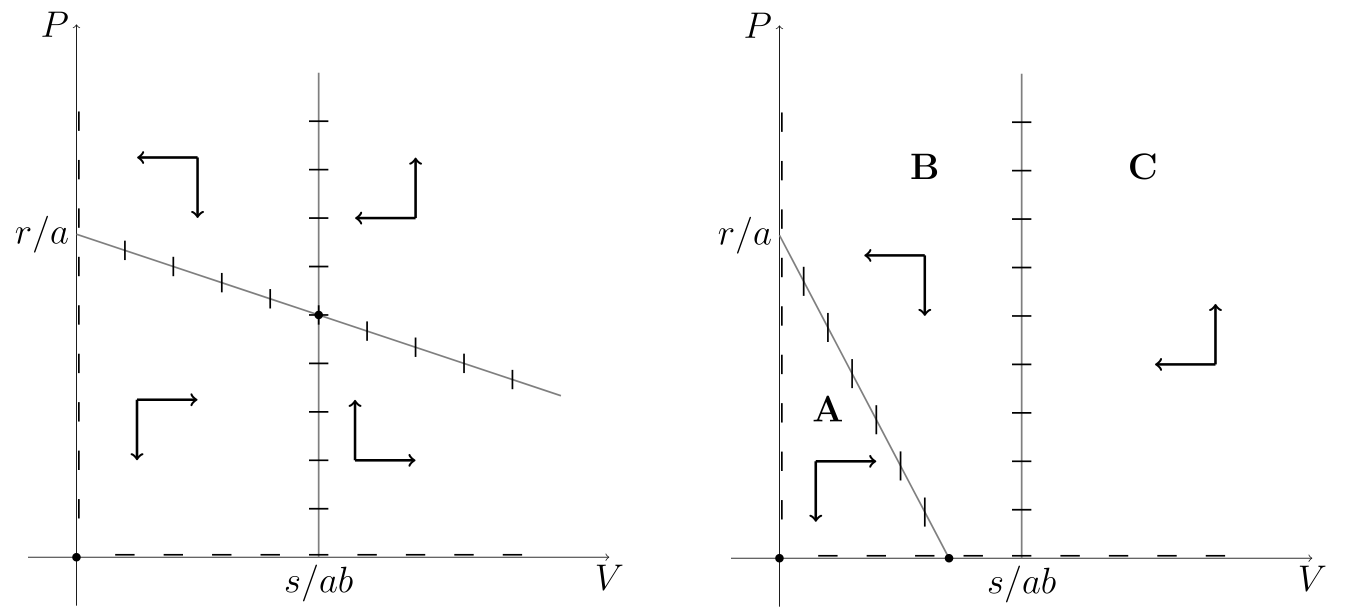
Jeśli izokliny nie przecinają się wewnątrz przestrzeni fazowej, to przestrzeń tę możemy podzielić na trzy obszary, por. rys. 7.1 i rys. 7.2: ![]() pod izokliną dla
pod izokliną dla ![]() ,
, ![]() nad tą izokliną i na lewo od izokliny dla
nad tą izokliną i na lewo od izokliny dla ![]() oraz
oraz ![]() — na prawo od izokliny dla
— na prawo od izokliny dla ![]() . Zauważmy, że rozwiązania dla warunku początkowego z
. Zauważmy, że rozwiązania dla warunku początkowego z ![]() muszą przejść do
muszą przejść do ![]() . Gdyby tak się nie stało, to mielibyśmy obie zmienne monotoniczne, przy czym zmienna
. Gdyby tak się nie stało, to mielibyśmy obie zmienne monotoniczne, przy czym zmienna ![]() pozostawałaby malejąca i ograniczona, a zmienna
pozostawałaby malejąca i ograniczona, a zmienna ![]() rosłaby nieograniczenie. W takim przypadku z pierwszego równania asymptotycznie dostajemy
rosłaby nieograniczenie. W takim przypadku z pierwszego równania asymptotycznie dostajemy ![]() , gdzie
, gdzie ![]() i
i ![]() są dodatnimi stałymi, czyli
są dodatnimi stałymi, czyli ![]() , co przeczy ograniczoności
, co przeczy ograniczoności ![]() . Zatem rozwiązanie przechodzi do
. Zatem rozwiązanie przechodzi do ![]() — tu obie zmienne są malejące, zatem albo pozostają w
— tu obie zmienne są malejące, zatem albo pozostają w ![]() i wobec tego mają granicę, czyli zbiegają do stanu stacjonarnego
i wobec tego mają granicę, czyli zbiegają do stanu stacjonarnego ![]() na brzegu obszaru, albo przechodzą do
na brzegu obszaru, albo przechodzą do ![]() . W
. W ![]() obie zmienne także są monotoniczne, tyle że
obie zmienne także są monotoniczne, tyle że ![]() rośnie. Przebieg pola wektorowego pokazuje, że rozwiązania nie mogą wyjść z obszaru
rośnie. Przebieg pola wektorowego pokazuje, że rozwiązania nie mogą wyjść z obszaru ![]() , więc także są zbieżne i zbiegają do
, więc także są zbieżne i zbiegają do ![]() .
.
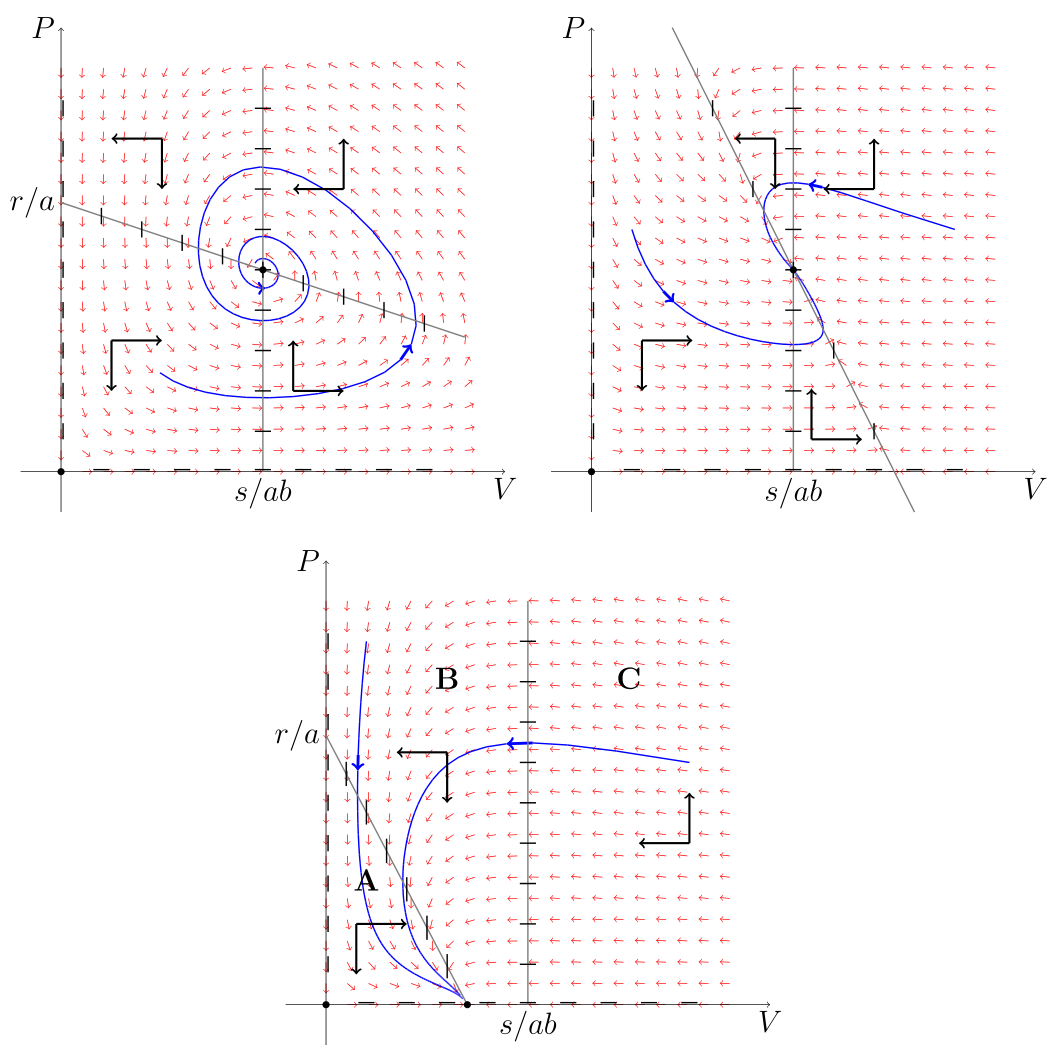
W drugim przypadku, gdy istnieje dodatni stan stacjonarny, przebieg pola wektorowego wskazuje, podobnie jak dla modelu Lotki – Volterry, że rozwiązania okrążają punkt krytyczny ![]() w przestrzeni fazowej, por. rys. 7.1 i rys. 7.2. Wartości własne dla tego punktu implikują, że jest on lokalnie stabilny, ale na takiej podstawie nie możemy wykluczyć istnienia orbit zamkniętych, czyli cykli granicznych. Można to próbować wykazać na różne sposoby, w tym przypadku dzięki prostocie modelu działa kilka standardowych metod. Najprostszy sposób w przypadku układów dwuwymiarowych polega na zastosowaniu kryterium Dulaca – Bendixsona. Dla danego układu o prawej stronie opisanej funkcją
w przestrzeni fazowej, por. rys. 7.1 i rys. 7.2. Wartości własne dla tego punktu implikują, że jest on lokalnie stabilny, ale na takiej podstawie nie możemy wykluczyć istnienia orbit zamkniętych, czyli cykli granicznych. Można to próbować wykazać na różne sposoby, w tym przypadku dzięki prostocie modelu działa kilka standardowych metod. Najprostszy sposób w przypadku układów dwuwymiarowych polega na zastosowaniu kryterium Dulaca – Bendixsona. Dla danego układu o prawej stronie opisanej funkcją ![]() rozważamy pewną funkcję
rozważamy pewną funkcję ![]() klasy
klasy ![]() , przy czym
, przy czym
nie zmienia znaku w ![]() . Wtedy w
. Wtedy w ![]() nie ma cykli, w szczególności nie ma cykli granicznych. Typowo stosowana funkcja
nie ma cykli, w szczególności nie ma cykli granicznych. Typowo stosowana funkcja ![]() ma postać
ma postać ![]() . W przypadku układu (7.1) dostajemy
. W przypadku układu (7.1) dostajemy
z czego wnioskujemy globalną stabilność stanu stacjonarnego ![]() , gdyż jeśli nie ma cyklu granicznego, to z twierdzenia Poincarégo – Bendixsona wszystkie rozwiązania zbiegają do stanu stacjonarnego, w tym przypadku do jedynego stanu stabilnego
, gdyż jeśli nie ma cyklu granicznego, to z twierdzenia Poincarégo – Bendixsona wszystkie rozwiązania zbiegają do stanu stacjonarnego, w tym przypadku do jedynego stanu stabilnego ![]() .
.
Bardziej uniwersalna metoda (działająca także w przypadku modeli o większej liczbie zmiennych) polega na znalezieniu funkcjonału Lapunowa. W tym przypadku można zastosować funkcjonał Lapunowa zaproponowany dla modelu Lotki – Volterry. W celu uproszczenia obliczeń przeprowadźmy najpierw zamianę zmiennych ![]() ,
, ![]() , która przesuwa stan stacjonarny do punktu
, która przesuwa stan stacjonarny do punktu ![]() . Zauważmy, że po zamianie zmiennych powstaje nowa przestrzeń fazowa
. Zauważmy, że po zamianie zmiennych powstaje nowa przestrzeń fazowa ![]() , a układ (7.1) przyjmuje postać
, a układ (7.1) przyjmuje postać
![\begin{array}[]{cclcl}\dot{x}&=&r(x+\bar{V})\left(1-\frac{x+\bar{V}}{K}\right)-a(x+\bar{V})(y+\bar{P})&=&-(x+\bar{V})\left(\frac{rx}{K}+ay\right),\\
\dot{y}&=&-s(y+\bar{P})+ab(x+\bar{V})(y+\bar{P})&=&abx(y+\bar{P}).\end{array}](wyklady/mbm/mi/mi523.png) |
(7.2) |
Funkcjonał Lapunowa dla układu (7.2) definiujemy jako
Należy teraz sprawdzić odpowiednie własności funkcjonału ![]() : w szczególności mamy
: w szczególności mamy ![]() w przestrzeni
w przestrzeni ![]() oraz
oraz ![]() (czyli
(czyli ![]() i
i ![]() ). Policzmy pochodną
). Policzmy pochodną ![]() wzdłuż trajektorii układu (7.2)
wzdłuż trajektorii układu (7.2)
dla ![]() i
i ![]() . Wynika stąd globalna stabilność dodatniego stanu stacjonarnego. Aby wykazać jego globalną asymptotyczną stabilność wystarczy udowodnić, że
. Wynika stąd globalna stabilność dodatniego stanu stacjonarnego. Aby wykazać jego globalną asymptotyczną stabilność wystarczy udowodnić, że ![]() jest ściśle malejąca, co pozostawiamy jako ćwiczenie.
jest ściśle malejąca, co pozostawiamy jako ćwiczenie.
Zauważmy, że tak zdefiniowany układ ma stany stacjonarne asymptotycznie stabilne, przy czym dla ![]() wszystkie rozwiązania (oprócz rozwiązań na brzegu przestrzeni fazowej) zbiegają do stanu stacjonarnego
wszystkie rozwiązania (oprócz rozwiązań na brzegu przestrzeni fazowej) zbiegają do stanu stacjonarnego ![]() , natomiast dla
, natomiast dla ![]() mamy zbieżność do dodatniego stanu stacjonarnego
mamy zbieżność do dodatniego stanu stacjonarnego ![]() , a przy
, a przy ![]() następuje bifurkacja siodło – węzeł. Taki typ bifurkacji oznacza, że zmienia się charakter punktu krytycznego z siodła na węzeł, przy czym dla bifurkacyjnej wartości
następuje bifurkacja siodło – węzeł. Taki typ bifurkacji oznacza, że zmienia się charakter punktu krytycznego z siodła na węzeł, przy czym dla bifurkacyjnej wartości ![]() parametru
parametru ![]() ze stanu stacjonarnego
ze stanu stacjonarnego ![]() bifurkuje dodatni stan stacjonarny i dla takiego
bifurkuje dodatni stan stacjonarny i dla takiego ![]() rozwiązania te sklejają się w jedno i choć nie przeprowadziliśmy analizy portretu fazowego dla tego przypadku, to doświadczenia związane z badaniem przebiegu orbit w pozostałych przypadkach pozwalają nam wnioskować, że także i dla bifurkacyjnej wartości
rozwiązania te sklejają się w jedno i choć nie przeprowadziliśmy analizy portretu fazowego dla tego przypadku, to doświadczenia związane z badaniem przebiegu orbit w pozostałych przypadkach pozwalają nam wnioskować, że także i dla bifurkacyjnej wartości ![]() mamy globalną stabilność stanu stacjonarnego
mamy globalną stabilność stanu stacjonarnego ![]() .
Zauważmy dalej, że niewielka zmiana prawej strony układu nie prowadzi w przypadku tego modelu do drastycznych zmian zachowania rozwiązań, zatem taki układ nie ma już niepożądanej własności niestabilności strukturalnej charakteryzującej układ (6.1).
.
Zauważmy dalej, że niewielka zmiana prawej strony układu nie prowadzi w przypadku tego modelu do drastycznych zmian zachowania rozwiązań, zatem taki układ nie ma już niepożądanej własności niestabilności strukturalnej charakteryzującej układ (6.1).
7.2. Model z kryjówkami dla ofiar
Inny sposób na uzyskanie stabilności strukturalnej stanowi przyjęcie założenia, że część ofiar jest stale niedostępna dla drapieżników — w środowisku występuje pewna liczba kryjówek, w których może się schować określona liczba ofiar. Niech liczba ofiar, która może się schować przed drapieżnikiem wynosi ![]() . Jeśli zatem w chwili początkowej
. Jeśli zatem w chwili początkowej ![]() liczebność całkowita ofiar
liczebność całkowita ofiar ![]() nie przekracza
nie przekracza ![]() , to wszystkie ofiary chowają się przed drapieżnikami i drapieżniki nie są w stanie nic upolować. W takiej sytuacji liczebność ofiar rośnie i w pewnym momencie przekracza
, to wszystkie ofiary chowają się przed drapieżnikami i drapieżniki nie są w stanie nic upolować. W takiej sytuacji liczebność ofiar rośnie i w pewnym momencie przekracza ![]() — dopiero wtedy możemy mówić o właściwym układzie drapieżnik – ofiara i zastosować odpowiedni model. W modelu tym zakładamy, że liczba ofiar dostępnych dla drapieżników wynosi
— dopiero wtedy możemy mówić o właściwym układzie drapieżnik – ofiara i zastosować odpowiedni model. W modelu tym zakładamy, że liczba ofiar dostępnych dla drapieżników wynosi ![]() ,
, ![]() , zatem tylko takie ofiary mogą zostać upolowane i wpłynąć na rozwój populacji drapieżników. Wyjściowy model Lotki – Volterry przyjmuje przy takim założeniu postać
, zatem tylko takie ofiary mogą zostać upolowane i wpłynąć na rozwój populacji drapieżników. Wyjściowy model Lotki – Volterry przyjmuje przy takim założeniu postać
![\begin{array}[]{ccl}\dot{V}&=&rV-a(V-K)P,\\
\dot{P}&=&-sP+ab(V-K)P,\end{array}](wyklady/mbm/mi/mi595.png) |
(7.3) |
przy czym parametry ![]() ,
, ![]() ,
, ![]() ,
, ![]() mają takie same znaczenie jak dla układu (6.1), natomiast
mają takie same znaczenie jak dla układu (6.1), natomiast ![]() oznacza tu liczbę kryjówek (w odróżnieniu od typowego oznaczenia pojemności środowiska).
oznacza tu liczbę kryjówek (w odróżnieniu od typowego oznaczenia pojemności środowiska).
Lokalne istnienie i jednoznaczność rozwiązań układu (7.3) ponownie wynikają z wielomianowej postaci prawej strony układu. Ponieważ model ma sens dla ![]() , to ograniczymy nasze rozważania do przestrzeni fazowej
, to ograniczymy nasze rozważania do przestrzeni fazowej ![]() . Zauważmy, że
. Zauważmy, że
Stwierdzenie 7.2
Zbiór ![]() jest przestrzenią niezmienniczą dla układu (7.3).
jest przestrzenią niezmienniczą dla układu (7.3).
Niech ![]() będzie warunkiem początkowym. Jeśli
będzie warunkiem początkowym. Jeśli ![]() , to
, to ![]() i rozwiązanie pozostaje na osi poziomej, co więcej, żadne rozwiązanie z wnętrza przestrzeni fazowej
i rozwiązanie pozostaje na osi poziomej, co więcej, żadne rozwiązanie z wnętrza przestrzeni fazowej ![]() nie osiągnie tego brzegu ze względu na jednoznaczność rozwiązań. Niech
nie osiągnie tego brzegu ze względu na jednoznaczność rozwiązań. Niech ![]() . Wtedy
. Wtedy ![]() , zatem rozwiązanie rośnie w pewnym przedziale czasu. Jeśli istnieje chwila
, zatem rozwiązanie rośnie w pewnym przedziale czasu. Jeśli istnieje chwila ![]() , w której rozwiązanie osiąga punkt na brzegu,
, w której rozwiązanie osiąga punkt na brzegu, ![]() , to oczywiście
, to oczywiście ![]() , zatem takie rozwiązanie nie może przekroczyć tego brzegu tego brzegu z prawej strony na lewą. Stąd
, zatem takie rozwiązanie nie może przekroczyć tego brzegu tego brzegu z prawej strony na lewą. Stąd ![]() dla wszystkich
dla wszystkich ![]() .
.
Z niezmienniczości zbioru ![]() wynika od razu globalne istnienie rozwiązań: dla zmiennej
wynika od razu globalne istnienie rozwiązań: dla zmiennej ![]() dostajemy oszacowanie liniowe
dostajemy oszacowanie liniowe ![]() , czyli
, czyli ![]() i dalej na każdym ograniczonym przedziale
i dalej na każdym ograniczonym przedziale ![]() szacujemy
szacujemy ![]() , gdzie
, gdzie ![]() , podobnie jak w przypadku układu (6.1).
, podobnie jak w przypadku układu (6.1).
Asymptotykę układu (7.3) badamy znanymi już metodami. Przeprowadzenie analizy portretu fazowego z zastosowaniem np. kryterium Dulaca – Bedixsona pozwala wysnuć następujący wniosek
Wniosek 7.1
Wszystkie rozwiązania układu (7.3) z warunkiem początkowym ![]() , takim że
, takim że ![]() ,
, ![]() , zbiegają asymptotycznie do dodatniego stanu stacjonarnego
, zbiegają asymptotycznie do dodatniego stanu stacjonarnego ![]() ,
, ![]() ,
, ![]() .
.
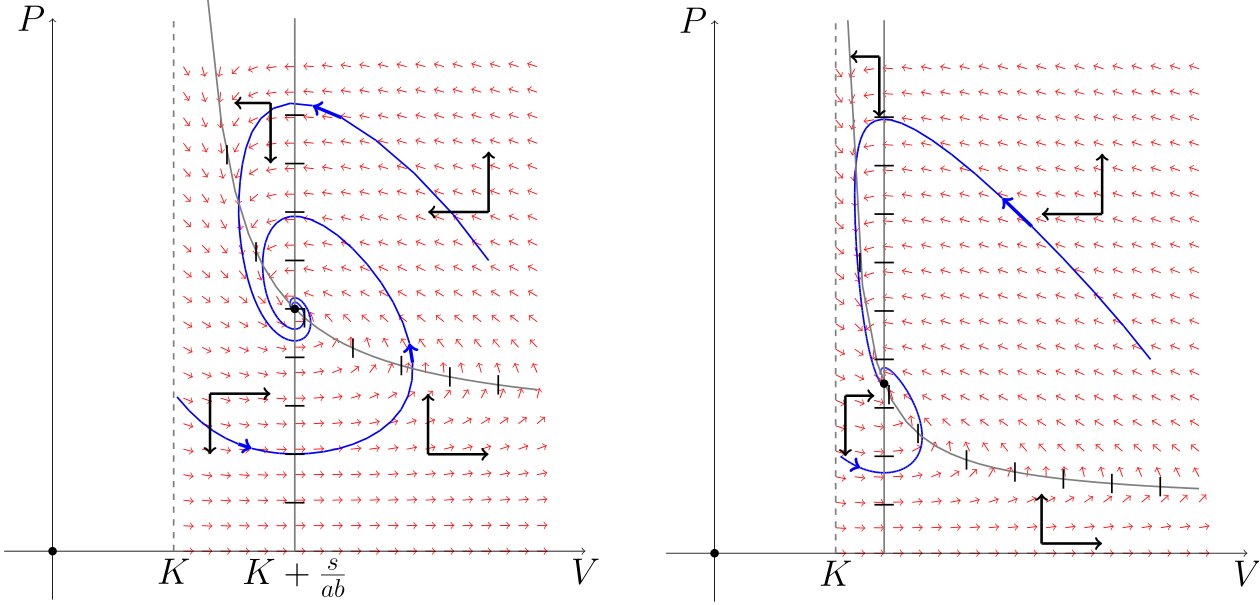
Zauważmy też, że podobnie jak dla układu (7.1), dodatni stan stacjonarny w zależności od parametrów (np. liczby ofiar mogących schować się w kryjówkach) może być albo ogniskiem, albo węzłem stabilnym, por. rys. 7.4.
Podsumowując — zarówno w przypadku modelu z kryjówkami dla ofiar jak i z pojemnością środowiska dostaliśmy globalną stabilność jednego ze stanów stacjonarnych, przy czym w przypadku modelu z kryjówkami jest to dodatni stan stacjonarny, natomiast w przypadku modelu z ograniczoną pojemnością środowiska może to być albo dodatni stan stacjonarny, albo stan brzegowy opisujący wyginięcie (ekstynkcję) populacji drapieżników. Jeśli stabilny stan stacjonarny jest węzłem, to rozwiązania od pewnego momentu ![]() pozostają monotoniczne, natomiast jeśli jest ogniskiem, to obserwujemy oscylacje i — ze względu na globalną stabilność — są to oscylacje gasnące.
pozostają monotoniczne, natomiast jeśli jest ogniskiem, to obserwujemy oscylacje i — ze względu na globalną stabilność — są to oscylacje gasnące.