Zagadnienia

9.1 Łańcuchy Markowa
9.2 Klasyfikacja stanów i łańcuchów

9. Doświadczenia Mendla: łańcuchy Markowa w klasycznej genetyce I

W kolejnych wykładach przejdziemy do omówienia podstaw genetyki klasycznej, w szczególności praw dziedziczenia postulowanych przez Mendla na podstawie wyników przeprowadzonych przez niego doświadczeń. Gregor Mendel, żyjący w XIX wieku czeski zakonnik, przez wiele lat zajmował się pracą w ogrodzie. Hodował różne rośliny, w szczególności groszek w dwóch odmianach — o strąkach zielonych i żółtych. Mendel zauważył, że można wyróżnić groszki ,,czysto żółte”, ,,czysto zielone” i ,,mieszane”. Jeśli krzyżuje się dwie rośliny, jedną ,,czysto żółtą”, a drugą ,,czysto zieloną”, to w następnym pokoleniu otrzymuje się rośliny o strąkach zielonych, natomiast przy dalszym krzyżowaniu ze sobą tak otrzymanych roślin, w kolejnym pokoleniu $3/4$ osobników ma strąki zielone, a $1/4$ żółte. Wyniki swoich badań opublikował w 1866 roku i na ich podstawie wysnuł teorię, którą obecnie nazywamy całkowitą dominacją genów.

W opisie doświadczeń Mendla będziemy używać stosowanych obecnie w genetyce pojęć, w szczególności jednostki kodujące dane cechy nazywać będziemy genami. Cecha badana przez Mendla, czyli kolor strąków groszku, kodowana jest przez parę genów, dziedziczonych po jednym od każdego z rodziców. Gen występuje w dwóch odmianach, które nazywamy allelami: dominującej, którą oznaczymy $D$ i recesywnej $R$ . Mamy więc trzy genotypy: $DD$ , $DR$ , $RR$ , ponieważ nie rozróżniamy kolejności występowania genów, zatem $DR$ i $RD$ dają ten sam genotyp. Jeśli w genotypie pojawia się choć jeden gen dominujący, to odpowiadająca mu cecha uwidacznia się w danym osobniku, czyli taki groszek ma strąki zielone. Rozróżniamy więc dwa fenotypy — genotypom $DD$ i $DR$ odpowiada fenotyp zielony, natomiast $RR$ ma fenotyp żółty. W zależności od genotypu, stosujemy też następujące nazewnictwo:

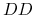$DD$ to osobnik (czysto) dominujący;
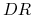$DR$ to hybryda;
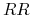$RR$ to osobnik (czysto) recesywny.

W teorii Mendla zakłada się, że osobniki łączą się losowo i potomek dziedziczy losowo po jednym genie od każdego z rodziców, przy czym wybór genów od rodziców jest niezależny. Sprawdźmy więc, jaki genotyp ma potomstwo ustalonej pary rodziców:

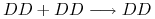$DD+DD\longrightarrow DD$ , jeśli krzyżujemy dwa osobniki dominujące, to z prawdopodobieństwem 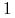$1$ potomek dziedziczy od każdego z rodziców gen dominujący $D$ , zatem każdy potomek ma ten sam genotyp $DD$ ;
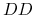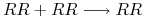$RR+RR\longrightarrow RR$ , podobnie jeśli krzyżujemy dwa osobniki recesywne, to z prawdopodobieństwem 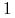$1$ potomek dziedziczy od każdego z rodziców gen dominujący 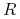$R$ , zatem każdy potomek ma ten sam genotyp $RR$ ;
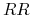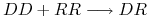$DD+RR\longrightarrow DR$ , jeśli krzyżujemy osobnika dominującego z recesywnym, to z prawdopodobieństwem 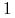$1$ potomek dziedziczy od jednego z rodziców gen 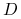$D$ , a od drugiego gen 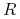$R$ , zatem każdy potomek jest hybrydą;
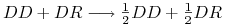$DD+DR\longrightarrow\frac{1}{2}DD+\frac{1}{2}DR$ , przy krzyżowaniu osobnika dominującego z hybrydą od osobnika dominującego potomek dziedziczy gen 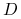$D$ z prawdopodobieństwem 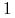$1$ , natomiast od hybrydy — albo gen 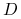$D$ z prawdopodobieństwem 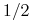$1/2$ , albo gen 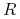$R$ , także z prawdopodobieństwem 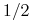$1/2$ , zatem potomek jest z prawdopodobieństwem 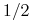$1/2$ albo hybrydą, albo dominantą;
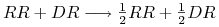$RR+DR\longrightarrow\frac{1}{2}RR+\frac{1}{2}DR$ , podobnie przy krzyżowaniu osobnika recesywnego z hybrydą potomek jest z prawdopodobieństwem 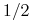$1/2$ albo recesywny, albo hybrydyczny;
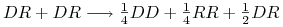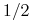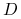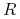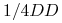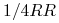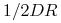$DR+DR\longrightarrow\frac{1}{4}DD+\frac{1}{4}RR+\frac{1}{2}DR$ , jeśli natomiast krzyżujemy dwie hybrydy, to z prawdopodobieństwem $1/2$ osobnik dziedziczy albo $D$ , albo $R$ od każdego z rodziców, stąd mamy rozkład genotypów potomka $1/4DD$ , $1/4RR$ oraz $1/2DR$ (pamiętając, że nie rozróżniamy układu 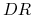$DR$ i $RD$ ).

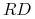Przedstawiony powyżej rozkład genotypów pokazuje, skąd w doświadczeniu Mendla wzięły się proporcje $3/4$ strąków zielonych i $1/4$ strąków żółtych. Jeśli bowiem Mendel skrzyżował w pierwszym pokoleniu osobnika czysto dominującego z czysto recesywnym, to każdy osobnik potomny był hybrydą. Następnie krzyżując hybrydy, jeśli tylko potomków w drugiej generacji było dostatecznie dużo, otrzymywał rozkład genotypów odpowiadający proporcjom: po $1/4$ osobników dominujących i recesywnych oraz $1/2$ hybryd, co uzewnętrzniło się jako $1/4$ fenotypu żółtego i $3/4$ fenotypu zielonego.

Tego typu doświadczenia można oczywiście powtarzać, ale jeśli znamy genotyp rodziców, to wiemy też, jaki powinien być wynik doświadczenia. Znacznie ciekawsze doświadczenie może polegać na tym, że na podstawie otrzymanych wyników eksperymentów chcemy wnioskować na temat genotypu rodziców. Opiszemy trzy takie doświadczenia, które nazwiemy ciągłym krzyżowaniem z osobnikiem dominującym, recesywnym i hybrydą. Każde z tych doświadczeń przeprowadzamy w taki sam sposób: ustalamy jednego z rodziców (wybieramy osobnika o danym genotypie) i krzyżujemy go z osobnikiem o genotypie nieznanym. Zakładamy, że mamy dostatecznie dużo potomstwa, tak by rozkład genotypów odpowiadał prawdopodobieństwom obliczonym na podstawie prawa Mendla, wybieramy losowo jednego potomka i ponownie krzyżujemy go z tym samym ustalonym osobnikiem. Doświadczenie powtarzamy wielokrotnie. Otrzymujemy więc ciąg doświadczeń, w których wynik kolejnego doświadczenia zależy od wyniku poprzedniego, mamy więc łańcuch Markowa. W celu zinterpretowania wyników eksperymentów przypomnimy podstawowe pojęcia i twierdzenia z teorii łańcuchów Markowa [7, 1].

9.1. Łańcuchy Markowa

Zajmiemy się teraz opisem ciągu zależnych doświadczeń losowych. Niech $\mathcal{D}$ oznacza pewne doświadczenie, którego zbiór możliwych wyników $\mathcal{W}_{1}$ , $\mathcal{W}_{2},\ldots,\mathcal{W}_{n}$ , $n\in\mathbb{N}$ , znamy. W trakcie powtarzania tego doświadczenia w próbie z numerem $t\in\mathbb{N}$ dostajemy wynik o numerze $X_{t}\in\{ 1,2,\ldots,n\}$ , przy czym prawdopodobieństwa różnych wartości $\mathcal{W}_{{X_{t}}}$ w ogólnym przypadku mogą zależeć od wyników wszystkich poprzednich doświadczeń. Taki obiekt nazwiemy skończonym procesem stochastycznym. Z kolei łańcuch Markowa to pewien szczególny rodzaj procesu stochastycznego, w którym wynik kolejnej próby zależy tylko od wyniku próby poprzedniej.

Definicja 9.1

Niech $\{ X_{t}\} _{{t=0}}^{{\infty}}$ oznacza ciąg zmiennych losowych o wartościach całkowitych. Jeśli w próbie z numerem $t$ zrealizowało się zdarzenie $\mathcal{W}_{j}$ , to przyjmiemy $X_{t}=j$ . Ciąg zmiennych losowych $\{ X_{t}\} _{{t=0}}^{{\infty}}$ nazwiemy łańcuchem Markowa, jeśli

$P\left(X_{t}=j|X_{0}=k_{0},X_{1}=k_{1},\ldots,X_{{t-1}}=i\right)=P\left(X_{t}=j|X_{{t-1}}=i\right),$

przy czym jeśli $P\left(X_{t}=j|X_{{t-1}}=i\right)$ nie zależy od numeru próby $t$ , to taki łańcuch nazywamy jednorodnym. Wyniki poszczególnych prób nazwiemy stanami łańcucha.

Podamy teraz kilka prostych przykładów:

— Rzut monetą to jeden z najprostszych możliwych procesów stochastycznych. Mamy dwa możliwe wyniki każdej próby orzeł $\mathcal{O}$ i reszka $\mathcal{R}$ , przy czym zawsze prawdopodobieństwo otrzymania każdego z tych dwóch wyników wynosi $1/2$ , niezależnie od tego, jakie wyniki otrzymywaliśmy w przeszłości. Wobec tego rzut monetą jest przykładem jednorodnego łańcucha Markowa.

— Rosyjska ruletka I to wersja gry, w której używa się sześciostrzałowego rewolweru z jedną kulą. Po zakręceniu bębenkiem oddaje się strzał i w pierwszej próbie wynik z prawdopodobieństwem $1/6$ jest martwy $\mathcal{M}$ , a z prawdopodobieństwem $5/6$ — żywy $\mathcal{Z}$ . Wynik kolejnej próby zależy od poprzedniego. Jeśli osoba, do której się strzela, została zastrzelona w poprzedniej próbie, to oczywiście w każdej następnej jest martwa z prawdopodobieństwem $1$ , natomiast jeśli jest żywa, to w drugiej próbie będzie martwa z prawdopodobieństwem $4/5$ , w trzeciej z prawdopodobieństwem $3/4$ , następnie $2/3$ , $1/2$ i ostatecznie w szóstej próbie wynik jest zawsze $\mathcal{M}$ z prawdopodobieństwem $1$ . Widzimy więc, że taka wersja rosyjskiej ruletki stanowi łańcuch Markowa, ale nie jest to łańcuch jednorodny.

— Rosyjska ruletka II to inna wersja, w której za każdym razem używa się sześciostrzałowego rewolweru z jedną kulą, ale przed każdą próbą ponownie kręci się bębenkiem. Zatem przy każdej próbie otrzymywane wyniki są jednakowe: $\mathcal{M}$ z prawdopodobieństwem $1/6$ oraz $\mathcal{Z}$ z prawdopodobieństwem $5/6$ . Mamy więc jednorodny łańcuch Markowa.

W dalszej części wykładu zajmiemy się tylko łańcuchami jednorodnymi, wobec tego nie będziemy już powtarzać określenia ,,jednorodny łańcuch Markowa”, tylko pisząc ,,łańcuch Markowa” będziemy mieli na myśli łańcuch jednorodny. Taki łańcuch Markowa możemy w jednoznaczny sposób zdefiniować podając jego stany, czyli możliwe wyniki kolejnych eksperymentów, oraz macierz przejścia $\mathbf{P}=(p_{{ij}})_{{i,j=1}}^{n}$ , czyli prawdopodobieństwa $p_{{ij}}$ przejścia ze stanu $\mathcal{W}_{i}$ w próbie $t-1$ do stanu $\mathcal{W}_{j}$ w kolejnej próbie $t$ . Macierz przejścia ma oczywiście następujące własności:

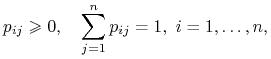$p_{{ij}}\geq 0,\quad\sum\limits _{{j=1}}^{n}p_{{ij}}=1,\ i=1,\ldots,n,$

ponieważ dla dowolnych $i,j\in\{ 1,\ldots,n\}$ liczba $p_{{ij}}$ jest prawdopodobieństwem, a jeśli łańcuch znajduje się w pewnym stanie $\mathcal{W}_{i}$ w chwili $t-1$ , to musi przejść do jakiegoś stanu $\mathcal{W}_{j}$ w chwili $t$ . Macierze o tych własnościach nazywamy macierzami stochastycznymi. Pełny opis łańcucha Markowa możemy także przedstawić za pomocą grafu skierowanego ważonego.

Definicja 9.2

Grafem skierowanym nazywamy parę $(\mathbb{W},S)$ , gdzie $\mathbb{W}$ jest zbiorem elementów nazywanych wierzchołkami grafu, natomiast $S$ stanowi zbiór uporządkowanych par wierzchołków, które nazywamy krawędziami grafu.

W przypadku grafu ważonego każdej istniejącej krawędzi prowadzącej od wierzchołka $i$ do $j$ przypisujemy pewną wagę $w_{{ij}}$ . Graf opisujący łańcuch Markowa budujemy w następujący sposób

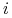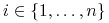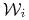wierzchołek z numerem $i$ , $i\in\{ 1,\ldots,n\}$ odpowiada wynikowi $\mathcal{W}_{i}$ ;
od wierzchołka z numerem 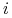$i$ do wierzchołka z numerem 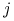$j$ przeprowadzamy krawędź 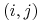$(i,j)$ , o ile 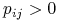$p_{{ij}}>0$ , a jeśli 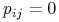$p_{{ij}}=0$ , to takiej krawędzi nie ma;
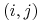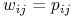zbudowanej krawędzi $(i,j)$ nadajemy wagę $w_{{ij}}=p_{{ij}}$ .

Zaprezentujemy teraz macierze przejścia i grafy przejścia, por. rys. 9.1, odpowiadające wymienionym w przykładach łańcuchom: rzutowi monetą i rosyjskiej ruletce w wersji II.

$\mathbf{P}_{{\text{rm}}}=\left(\begin{array}[]{cc}0,5&0,5\\ 0,5&0,5\end{array}\right),\quad\mathbf{P}_{{\text{rr}}}=\left(\begin{array}[]{cc}1&0\\ 1/6&5/6\end{array}\right).$

Macierze przejścia i grafy przejścia rzutowi monetą (z lewej) i rosyjskiej ruletce w wersji II (z prawej).

Rys. 9.1. Macierze przejścia i grafy przejścia odpowiadające rzutowi monetą (z lewej) i rosyjskiej ruletce w wersji II (z prawej).

Macierz przejścia $\mathbf{P}$ odzwierciedla dynamikę łańcucha w jednym kroku, natomiast my jak zwykle chcemy zbadać, co będzie się działo asymptotycznie, czyli czego możemy się spodziewać, jeśli będziemy nasze doświadczenia powtarzać dostatecznie długo. Do tego celu musimy obliczyć prawdopodobieństwa przejścia wyższego rzędu, czyli $p_{{ij}}^{{(t)}}$ , które opisuje przejście ze stanu $\mathcal{W}_{i}$ do stanu $\mathcal{W}_{j}$ w $t$ krokach, czyli po wykonaniu $t$ prób. Mamy więc $p_{{ij}}^{{(t)}}=P\left(X_{t}=j|X_{0}=i\right)$ . Zgodnie ze wzorem na prawdopodobieństwo całkowite dla $t>1$ otrzymujemy

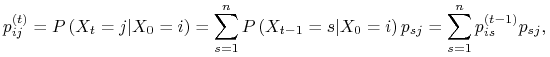$p_{{ij}}^{{(t)}}=P\left(X_{t}=j|X_{0}=i\right)=\sum\limits _{{s=1}}^{n}P\left(X_{{t-1}}=s|X_{0}=i\right)p_{{sj}}=\sum\limits _{{s=1}}^{n}p_{{is}}^{{(t-1)}}p_{{sj}},$

czyli rekurencyjną zależność $p_{{ij}}^{{(t)}}$ od prawdopodobieństw niższego rzędu $p_{{is}}^{{(t-1)}}$ . Stąd jeśli $\mathbf{P}^{{(t)}}=\left(p_{{ij}}^{{(t)}}\right)_{{i,j=1}}^{n}$ jest macierzą przejścia wyższego rzędu, to dostajemy zależność

$\mathbf{P}^{{(t)}}=\mathbf{P}^{{(t-1)}}\mathbf{P}\ \ \Longrightarrow\ \ \mathbf{P}^{{(t)}}=\mathbf{P}^{t}.$

Wnioskujemy zatem, że rozkład łańcucha w dowolnym kroku jest jednoznacznie wyznaczony przez macierz przejścia i początkowy rozkład prawdopodobieństwa $p_{i}^{0}=P(X_{0}=i)$ , $i=1,\ldots,n$ .

W kontekście opisywanych powyżej doświadczeń genetycznych chcemy poznać asymptotykę dwóch konkretnych typów łańcuchów Markowa. Zanim jednak przejdziemy do badania asymptotyki, podamy potrzebne definicje, w tym klasyfikację stanów łańcucha.

9.2. Klasyfikacja stanów i łańcuchów

Zaczniemy od podziału stanów łańcucha na pewne specjalne grupy.

Definicja 9.3

Stan $\mathcal{W}_{i}$ nazwiemy nieistotnym, jeśli istnieje taki stan $\mathcal{W}_{j}$ i liczba $t_{0}\in\mathbb{N}\setminus\{ 0\}$ , że $p_{{ij}}^{{(t_{0})}}>0$ oraz $p_{{ji}}^{{(t)}}=0$ dla dowolnego $t\in\mathbb{N}$ . W przypadku przeciwnym stan $\mathcal{W}_{i}$ nazywamy istotnym.

Definicja 9.4

Stany istotne $\mathcal{W}_{i}$ , $\mathcal{W}_{j}$ nazywamy komunikującymi się, jeśli istnieją takie $t$ , $s\in\mathbb{N}\setminus\{ 0\}$ , dla których $p_{{ij}}^{{(t)}}>0$ i $p_{{ji}}^{{(s)}}>0$ .

Podzielmy teraz wszystkie stany danego łańcucha na podklasy: niech $\mathcal{S}^{0}$ oznacza klasę wszystkich stanów nieistotnych, następnie wybierzmy jakikolwiek stan istotny $\mathcal{W}_{i}$ i oznaczmy przez $\mathcal{S}^{i}$ zbiór wszystkich stanów komunikujących się z $\mathcal{W}_{i}$ . Ten zbiór stanów nazywa się także czasem zbiorem stochastycznie zamkniętym. W taki sposób podzielimy łańcuch na rozłączne klasy stanów komunikujących się $\mathcal{S}^{1},\ldots,\mathcal{S}^{N}$ , $N\leq n$ . Jeśli łańcuch znalazł się w pewnym momencie w stanie istotnym $\mathcal{W}_{i}$ , to już nigdy nie wyjdzie z odpowiadającej mu klasy.

Definicja 9.5

Jeśli klasa $\mathcal{S}^{i}$ składa się z jednego stanu $\mathcal{W}_{i}$ , to taki stan nazywamy pochłaniającym (absorbującym).

Definicja 9.6

Łańcuch Markowa składający się z jednej klasy stanów istotnych komunikujących się nazywamy łańcuchem nieprzywiedlnym. Jeśli łańcuch zawiera więcej niż jedną klasę, to jest przywiedlny.

Badając łańcuch Markowa sprowadzamy najpierw jego macierz do postaci kanonicznej numerując stany w taki sposób, aby na początku znalazły się stany nieistotne, a następnie poszczególne stany z kolejnych klas. Macierz ma wtedy postać

$\mathbf{P}=\begin{array}[]{ccccc}&\mathcal{S}^{0}&\mathcal{S}^{1}&\mathcal{S}^{2}&\\ \mathcal{S}^{0}&\begin{array}[]{cc}\ldots&\ldots\\ \ldots&\ldots\end{array}&\begin{array}[]{cc}\ldots&\ldots\\ \ldots&\ldots\end{array}&\begin{array}[]{cc}\ldots&\ldots\\ \ldots&\ldots\end{array}&\begin{array}[]{cc}\ldots&\ldots\\ \ldots&\ldots\end{array}\\ \mathcal{S}^{1}&0&\begin{array}[]{cc}\vdots&\vdots\\ \vdots&\vdots\end{array}&0&0\\ \mathcal{S}^{2}&0&0&\begin{array}[]{cc}\vdots&\vdots\\ \vdots&\vdots\end{array}&0\\ \begin{array}[]{c}\vdots\\ \end{array}&&&&\\ \end{array},$

a powstałe macierze $\left(\begin{array}[]{cc}\vdots&\vdots\\ \vdots&\vdots\end{array}\right)$ są macierzami stochastycznymi i każda z nich odpowiada łańcuchowi nieprzywiedlnemu.

Oznaczmy

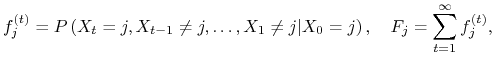$f_{j}^{{(t)}}=P\left(X_{t}=j,X_{{t-1}}\ne j,\ldots,X_{1}\ne j|X_{0}=j\right),\quad F_{j}=\sum\limits _{{t=1}}^{\infty}f_{j}^{{(t)}},$

gdzie $f_{j}^{{(t)}}$ oznacza prawdopodobieństwo, że układ po wyjściu ze stanu $\mathcal{W}_{j}$ wróci do tego stanu po raz pierwszy po $t$ krokach, a $F_{j}$ to prawdopodobieństwo, że po wyjściu z tego stanu wróci do niego kiedykolwiek.

– Stan $\mathcal{W}_{j}$ nazywamy powracającym, jeśli $F_{j}=1$ , natomiast niepowracającym, gdy $F_{j}<1$ .

– Stan $\mathcal{W}_{j}$ nazywamy zerowym, jeśli $p_{{jj}}^{{(t)}}\to 0$ przy $t\to\infty$ .

– Stan $\mathcal{W}_{j}$ nazywamy okresowym o okresie $d_{j}$ , jeśli powrót z dodatnim prawdopodobieństwem możliwy jest w liczbie kroków równej wielokrotności $d_{j}$ i $d_{j}$ jest najmniejszą liczbą o tej własności (czyli $d_{j}$ jest NWD zbioru $\{ t:\ p_{{jj}}^{{(t)}}>0\}$ ).

– Stan powracający, niezerowy i nieokresowy nazywamy ergodycznym.

Wymienimy teraz dwa typy łańcuchów, które są istotne z punktu widzenia doświadczeń genetycznych, jakie za ich pomocą chcemy opisywać.

Definicja 9.7

Łańcuchem pochłaniającym (absorbującym) nazwiemy taki łańcuch przywiedlny, którego klasy stanów istotnych składają się z pojedynczych stanów pochłaniających.

Drugi typ stanowią oczywiście łańcuchy nieprzywiedlne. Każdy typ łańcucha przywiedlnego możemy analizować korzystając z własności łańcuchów pochłaniających i łańcuchów nieprzywiedlnych. Dopóki łańcuch nie trafi do któregoś ze zbiorów $\mathcal{S}^{i}$ , $i>0$ , możemy traktować łańcuch jak łańcuch pochłaniający, natomiast jak już trafi do zbioru $\mathcal{S}^{i}$ , $i>0$ , to ten zbiór tworzy łańcuch nieprzywiedlny.

Wróćmy teraz do naszych prostych przykładów i spróbujmy w ich kontekście zastosować poznane definicje.

Rzut monetą: zauważmy, że prawdopodobieństwa przejścia z każdego z dwóch stanów łańcucha 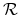$\mathcal{O}$ , $\mathcal{R}$ do każdego z nich jest zawsze równe 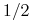$1/2$ , bez względu na stan w kroku poprzednim, zatem 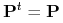$\mathbf{P}^{t}=\mathbf{P}$ , czyli oba stany są istotne i komunikujące się, tworzą więc łańcuch nieprzywiedlny.
Rosyjska ruletka II: stan 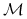$\mathcal{M}$ jest oczywiście pochłaniający, natomiast stan 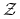$\mathcal{Z}$ tworzy zbiór 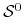$\mathcal{S}^{0}$ i jest stanem nieistotnym, ponieważ 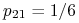$p_{{21}}=1/6$ , natomiast 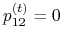$p_{{12}}^{{(t)}}=0$ dla dowolnego 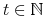$t\in\mathbb{N}$ , gdyż 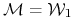$\mathcal{M}=\mathcal{W}_{1}$ jest pochłaniający, czyli łańcuch ma własności wymienione w def. 9.7, zatem stanowi łańcuch pochłaniający.

Zauważmy, że asymptotycznie te dwa typy łańcuchów (czyli nieprzywiedlny i pochłaniający) mają diametralnie różne własności. W łańcuchu nieprzywiedlnym każdy stan jest osiągany z dodatnim prawdopodobieństwem w dowolnej próbie, natomiast w łańcuchu pochłaniającym w pewnej próbie łańcuch wynosi trafia do jakiegoś stanu pochłaniającego, z którego już nie wychodzi. W przypadku rzutu monetą, ponieważ dla dowolnego $t\in\mathbb{N}\setminus\{ 0\}$ zachodzi $\mathbf{P}_{{\text{rm}}}^{t}=\mathbf{P}_{{\text{rm}}}$ , więc bez względu na liczbę prób zawsze średnio dostajemy połowę orłów i połowę reszek. Z kolei w przypadku rosyjskiej ruletki prawdopodobieństwo pozostania żywym maleje do $0$ wraz z rosnącą liczbą prób, co łatwo możemy bezpośrednio obliczyć iterując macierz przejścia