Zagadnienia
1. Równania ruchu
1.1. Wstęp
Mechanika klasyczna, a właściwie jej część zwana dynamiką, zajmuje się opisem ruchu ciał wynikającym z działania na nie sił. Zjawisko to może być obserwowane bez skomplikowanego sprzętu badawczego. Jego model matematyczny mechanika teoretyczna został najwcześniej rozwinięty i stał się podstawą dla innych działów fizyki matematycznej. Wprowadzając ten model, przyjmujemy ustalenia:
-
Przestrzeń fizyczną, będącą terenem naszych rozważań, opiszemy jako
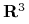 .
. -
Interesujące nas obiekty - ciała materialne - będziemy utożsamiać z pojedynczymi punktami
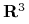 .
. -
Założymy, że istnieje absolutny czas. Wtedy ruch ciała - punktu materialnego - opiszemy, podając trzy aktualne współrzędne tego punktu. Zatem jego ewolucja to trójka funkcji
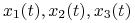 lub inaczej funkcja wektorowa o wartościach w
lub inaczej funkcja wektorowa o wartościach w 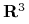 .
Dziedziną tej funkcji jest oś czasu lub jakiś jej podzbiór.
.
Dziedziną tej funkcji jest oś czasu lub jakiś jej podzbiór. -
Rozważanie skończonego układu punktów materialnych (a do takich układów ograniczymy się w tym wykładzie) można zastąpić rozważaniem jednego punktu materialnego w przestrzeni większego wymiaru: rozpatrując układ n punktów w
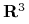 wyznaczamy
wyznaczamy 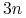 funkcji. Możemy te funkcje interpretować jako trajektorię jednego punktu w
funkcji. Możemy te funkcje interpretować jako trajektorię jednego punktu w 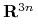 . To spojrzenie ułatwia nam obserwowanie aparatu matematycznego kosztem pewnego zaciemnienia tła fizycznego.
. To spojrzenie ułatwia nam obserwowanie aparatu matematycznego kosztem pewnego zaciemnienia tła fizycznego. -
Związek ruchu z wywołującego go siłą jest oparty na ”drugim prawie mechaniki Newtona”. Mówi ono, że w ustalonej chwili iloczyn masy bezwładnej ciała- parametru liczbowego -
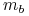 - i przyspieszenia ruchu ciała - wektora- jest proporcjonalny do działającej na ciało w tej samej chwili siły.
Matematycznie oznacza to (dla pojedynczego punktu materialnego), że trajektoria ruchu,
- i przyspieszenia ruchu ciała - wektora- jest proporcjonalny do działającej na ciało w tej samej chwili siły.
Matematycznie oznacza to (dla pojedynczego punktu materialnego), że trajektoria ruchu, 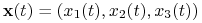 jest związana ze góry
zadaną siłą
jest związana ze góry
zadaną siłą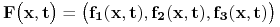
(1.1) 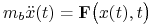
(1.2) za pomocą wektorowego równania różniczkowego (czyli układu 3 równań skalarnych) o postaci:
Siła
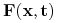 ma wartość w
ma wartość w 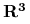 i jest określona na
i jest określona na 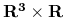 natomiast
natomiast 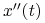 oznacza przyspieszenie ciała w tej samej chwili ,kiedy przechodzi ono przez punkt
oznacza przyspieszenie ciała w tej samej chwili ,kiedy przechodzi ono przez punkt 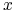 , a
, a 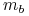 jest jego masą. W ogólnym przypadku
jest jego masą. W ogólnym przypadku 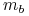 może też zależeć od czasu.
może też zależeć od czasu. -
Często występuje sytuacja, kiedy swoboda ruchu poszczególnych punktów układu jest poddana ograniczeniom zwanymi umownie więzami. Prowadzi to do sytuacji, kiedy zbiór możliwych położeń układu nie stanowi całej przestrzeni
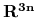 lecz jej podzbiór. Traktowany tutaj przypadek prowadzi do podzbiorów będących podrozmaitościami. Sytuacja taka dodaje do naszych rozważań interesujące aspekty geometryczne.
lecz jej podzbiór. Traktowany tutaj przypadek prowadzi do podzbiorów będących podrozmaitościami. Sytuacja taka dodaje do naszych rozważań interesujące aspekty geometryczne.
Dla wyjaśnienia powyższych ustaleń przedstawimy teraz kilka prostych przykładów. Dyskusja sytuacji bardziej skomplikowanych i refleksja nad ich strukturą stanowi przedmiot tego wykładu.
1.2. Przykłady równań ruchu
Zaczniemy od kilku ustaleń dotyczących zapisu:
Ze względu na to, że pochodne szukanych funkcji występują często podniesione do kwadratu lub też w innych kłopotliwych konfiguracjach, wygodnym będzie wprowadzenie innego ich oznaczania, niż zwykle przyjmowane w matematyce. Będziemy mianowicie pisać ![]() zamiast
zamiast ![]() i
i ![]() zamiast
zamiast
![]() .
Dla funkcji wektorowej
.
Dla funkcji wektorowej ![]() zapis
zapis ![]() będzie oznaczać kwadrat długości wektora
będzie oznaczać kwadrat długości wektora ![]() , t.j.
, t.j.
![]() , a
, a ![]() jego długość t.j.
jego długość t.j.
| (1.3) |
Przykład 1.1
Spadanie przedmiotów na Ziemię w pobliżu jej powierzchni bez uwzględniania oporu powietrza.
Zgodnie z obserwacjami (Stevin,Galileusz) wszystkie ciała znajdujące się blisko powierzchni Ziemi spadają tak samo, ze stałym przyspieszniem ![]() wynoszącym około
wynoszącym około ![]() . Orientując oś pionową w górę i umieszczając zero na powierzchni Ziemi, otrzymamy równanie opisujące spadanie ciał w formie:
. Orientując oś pionową w górę i umieszczając zero na powierzchni Ziemi, otrzymamy równanie opisujące spadanie ciał w formie:
| (1.4) |
Rozwiązanie równaniania (1.4) nie nastręcza trudności. Otrzymujemy kolejno ![]() a następnie
a następnie ![]() , gdzie
, gdzie ![]() i
i ![]() są stałymi.
Obecność dwóch stałych dowolnych w ogólnej postaci rozwiązania równania (1.4) oznacza, że do wyodrębnienia konkretnego rozwiązania potrzebne są dwa dodatkowe warunki. Ze względu na pewność istnienia rozwiązania przy poniższych warunkach (twierdzenie o istnieniu jednoznaczności) a także ze względu na ich prosty sens fizyczny, najczęściej przyjmowane są tzw. warunki początkowe: żądamy, aby w wybranej chwili
są stałymi.
Obecność dwóch stałych dowolnych w ogólnej postaci rozwiązania równania (1.4) oznacza, że do wyodrębnienia konkretnego rozwiązania potrzebne są dwa dodatkowe warunki. Ze względu na pewność istnienia rozwiązania przy poniższych warunkach (twierdzenie o istnieniu jednoznaczności) a także ze względu na ich prosty sens fizyczny, najczęściej przyjmowane są tzw. warunki początkowe: żądamy, aby w wybranej chwili ![]() nasze ciało znajdowało się w ustalonym punkcie
nasze ciało znajdowało się w ustalonym punkcie ![]() oraz aby miało zadaną prędkość
oraz aby miało zadaną prędkość ![]() .
Dla naszego rozwiązania warunki początkowe prowadzą do następujących równań na stałe
.
Dla naszego rozwiązania warunki początkowe prowadzą do następujących równań na stałe ![]() i
i ![]() :
:
| (1.5) |
z których wyznaczamy ![]() oraz
oraz
Najłatwiej przeprowadzić te rachunki, gdy ![]() . Wtedy po prostu
. Wtedy po prostu ![]() oraz
oraz ![]() .
.
Przykład 1.2
Spadanie przedmiotów na Ziemię w pobliżu jej powierzchni z uwzględnieniem oporu powietrza
Zauważmy, że równanie (1.4) możemy otrzymać z II prawa Newtona
| (1.6) |
gdzie ![]() jest masą bezwładną ciała a
jest masą bezwładną ciała a ![]() jego masą grawitacyjną. Wielkość występująca po prawej stronie (1.6) jest wtedy siłą, z jaką Ziemia przyciąga ku swojemu środkowi ciało o masie
jego masą grawitacyjną. Wielkość występująca po prawej stronie (1.6) jest wtedy siłą, z jaką Ziemia przyciąga ku swojemu środkowi ciało o masie ![]() , znajdujące się na jej powierzchni. (Zobacz Przykład 1.3 poniżej).
Ponieważ, jak wykazują wszystkie doświadczenia,
, znajdujące się na jej powierzchni. (Zobacz Przykład 1.3 poniżej).
Ponieważ, jak wykazują wszystkie doświadczenia, ![]() , upraszczając równanie (1.6) otrzymamy równanie (1.4).
Możemy teraz zmodyfikować równanie(1.2),dodając do siły po jego prawej stronie składnik reprezentujący opór powietrza. Zgodnie z doświadczeniem ma on postać
, upraszczając równanie (1.6) otrzymamy równanie (1.4).
Możemy teraz zmodyfikować równanie(1.2),dodając do siły po jego prawej stronie składnik reprezentujący opór powietrza. Zgodnie z doświadczeniem ma on postać
| (1.7) |
gdzie ![]() jest współczynnikiem zależnym od wyboru jednostek i zależnym od ośrodka stawiającego opór ( w naszym przypadku powietrza). Uwzlędniając równość
jest współczynnikiem zależnym od wyboru jednostek i zależnym od ośrodka stawiającego opór ( w naszym przypadku powietrza). Uwzlędniając równość ![]() otrzymamy jednowymiarowe równanie ruchu o postaci:
otrzymamy jednowymiarowe równanie ruchu o postaci:
| (1.8) |
Przykład 1.3
Spadanie z dużej wysokości
Oprzemy się na odkrytej przez Newtona zasadzie powszechnego ciążenia:
dwa ciała o masach grawitacyjnych ![]() i
i ![]() przyciągają się z siłą działającą wzdłuż prostej łączącej środki ich mas wprost proporcjonalną do iloczynu
przyciągają się z siłą działającą wzdłuż prostej łączącej środki ich mas wprost proporcjonalną do iloczynu ![]() i odwrotnie proporcjonalną do kwadratu odległości między nimi. Jeżeli
i odwrotnie proporcjonalną do kwadratu odległości między nimi. Jeżeli ![]() oznacza wektor położenia środka masy ciała o masie
oznacza wektor położenia środka masy ciała o masie ![]() a
a ![]() wektor położenia środka masy ciała o masie
wektor położenia środka masy ciała o masie ![]() , to siła działająca na drugie ciało ma postać:
, to siła działająca na drugie ciało ma postać:
| (1.9) |
W rezultacie, ograniczając nasze rozważania do prostej przechodzącej przez środek masy Ziemi i zorientowanej od tego środka, a następnie przyjmując jako zero punkt na osi i na powierzchni Ziemi, otrzymujemy z (1.9) równanie opisujące ruch po naszej osi 'spadanie z dużej wysokości' w postaci:
| (1.10) |
a ponieważ ![]() , redukując otrzymamy:
, redukując otrzymamy:
| (1.11) |
Zestawiając ten wynik z Przykładem 1.1 widzimy, że w tamtej sytuacji przyjęliśmy siłę za stałą i równą ![]() dla
dla ![]() , co stanowi dobre przybliżenie opisu (1.7) przy założeniu, że
, co stanowi dobre przybliżenie opisu (1.7) przy założeniu, że ![]() jest małe w porównaniu z
jest małe w porównaniu z ![]() .
.
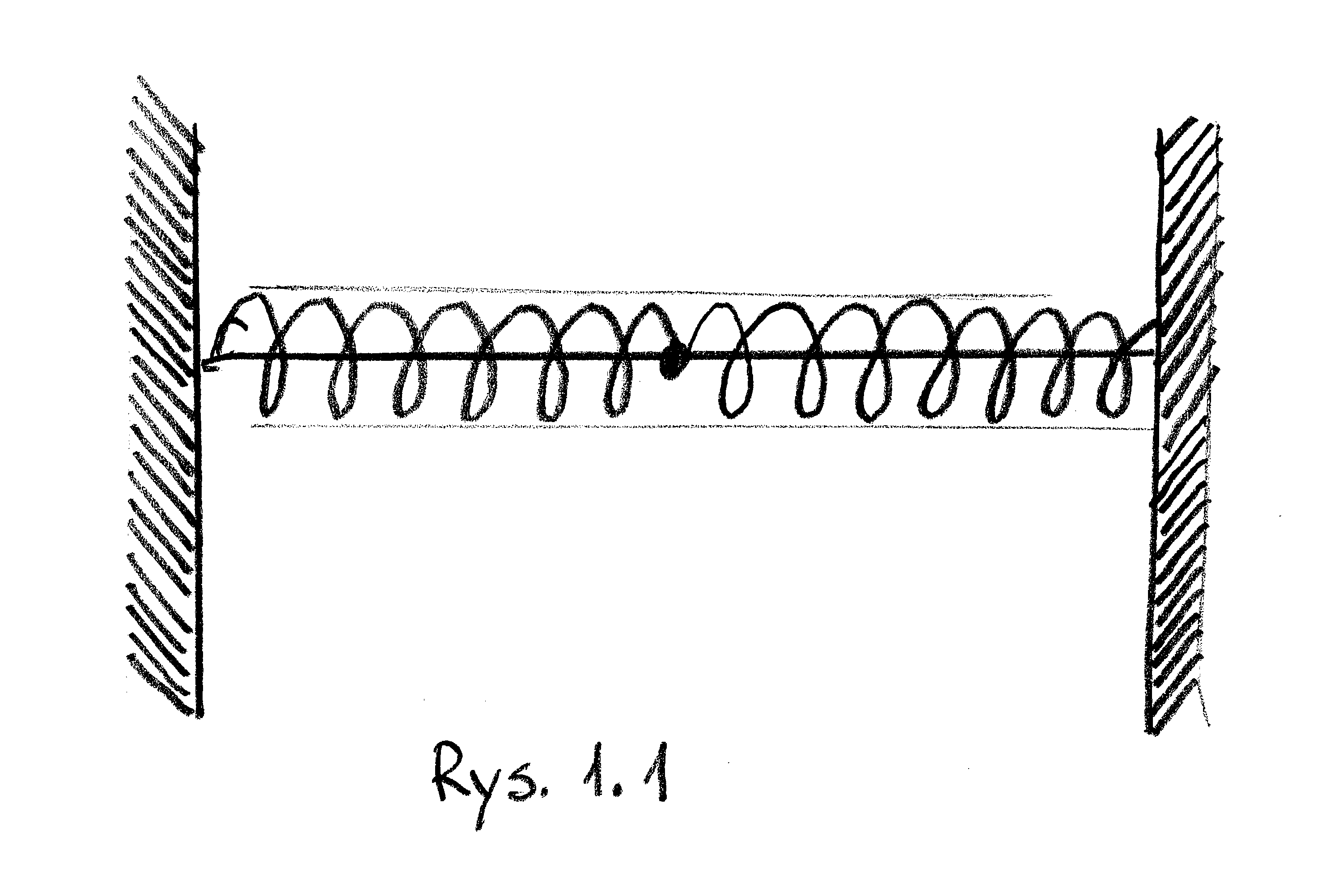
Przykład 1.4
Drgania sprężyste
Wyobrażmy sobie koralik o masie ![]() nanizany na pręt i przyciągany do obu końców pręta za pomocą takich samych sprężynek (rysunek poniżej):
nanizany na pręt i przyciągany do obu końców pręta za pomocą takich samych sprężynek (rysunek poniżej):
Umieśćmy oś na linii pręta. Wtedy, przyjmując za zero pozycję na środku pręta, o której założymy że jest położeniem równowagi, widzimy, że (zgodnie z prawem Hooka) wychylenie o ![]() od tego położenia wywołuje siłę -
od tego położenia wywołuje siłę -![]() ściągają koralik z powrotem do położenia równowagi.
Zatem zgodnie z II prawem Newtona równanie ruchu będzie miało postać:
ściągają koralik z powrotem do położenia równowagi.
Zatem zgodnie z II prawem Newtona równanie ruchu będzie miało postać:
| (1.12) |
gdzie ![]() jest współczynnikiem proporcjonalności zależnym od wyboru jednostek i od własności sprężyn.
jest współczynnikiem proporcjonalności zależnym od wyboru jednostek i od własności sprężyn.
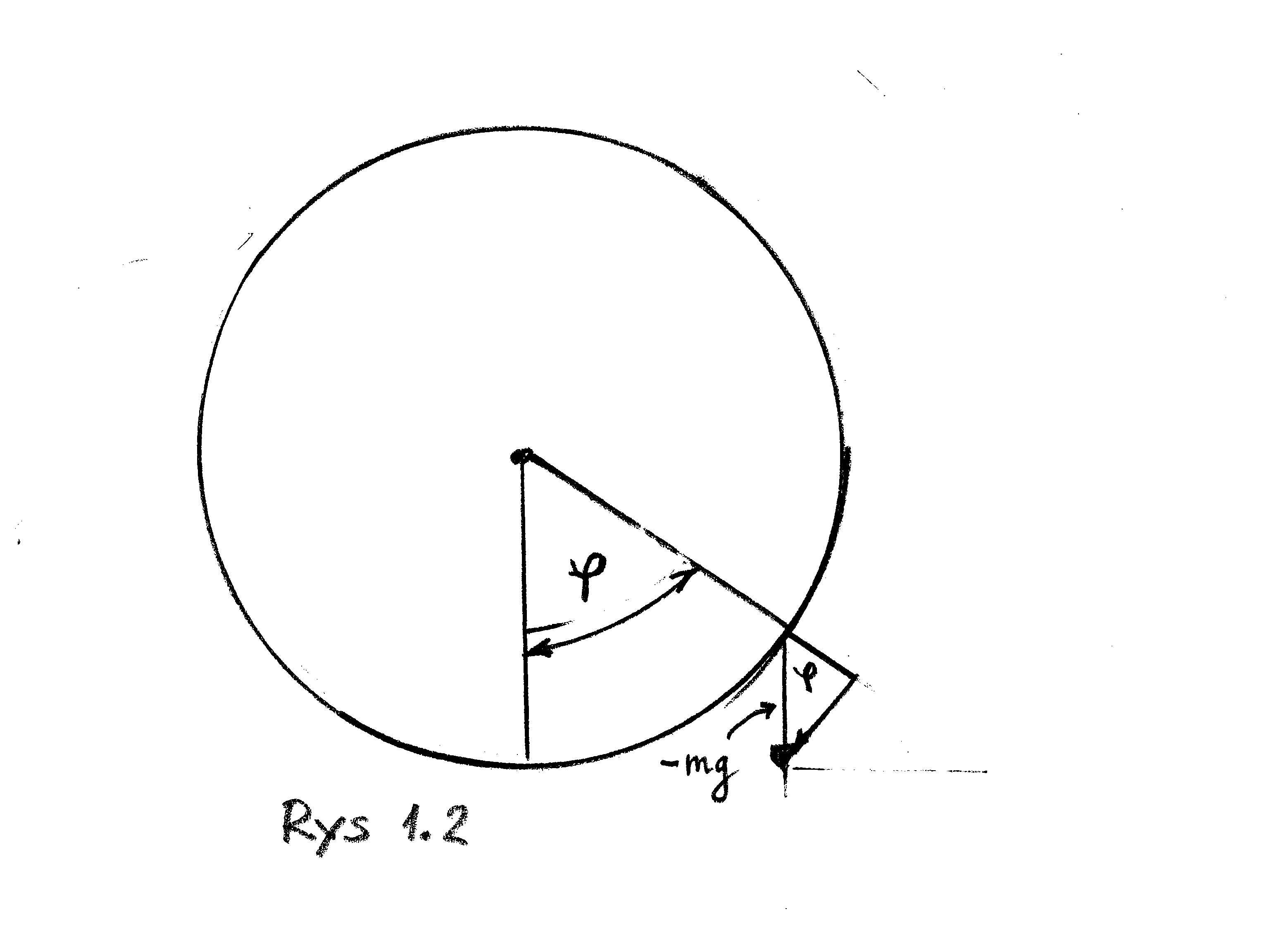
Przykład 1.5
Wahadło płaskie
Rozważmy punkt materialny o masie ![]() , znajdujący się w jednorodnym polu grawitacyjnym (jak w (1.2)) i pozostający przez cały czas w ustalonej płaszczyźnie pionowej. Załóżmy też, że jego odległość od ustalonego punktu w tej płaszczyźnie pozostaje stała.
, znajdujący się w jednorodnym polu grawitacyjnym (jak w (1.2)) i pozostający przez cały czas w ustalonej płaszczyźnie pionowej. Załóżmy też, że jego odległość od ustalonego punktu w tej płaszczyźnie pozostaje stała.
Jest to pierwszy z tej serii przykład układu z więzami. Chcąc opisać ten ruch możemy postąpić na dwa sposoby:
-
Do działającej siły dodać siły fikcyjne ”`siły reakcji więzów”', zastępując w ten sposób (dla punktów znajdujących się na rozmaitości) faktycznie działającą siłę jej rzutem na hiperpłaszczyznę styczną do rozmaitośći. (Metodę tę omówimy systematycznie w dalszym kursie wykładu)
-
Drugim sposobem jest lokalne sparametryzowanie rozmaitości i zapisanie składowej stycznej działającej siły jako funkcji parametrów. Postępowanie to w przypadku naszego przykładu objaśnia poniższy rysunek:
Otrzymamy w ten sposób równanie opisujące niejako fikcyjny ruch w fikcyjnym świecie ograniczonym do naszej rozmaitości. Okazuje się, że metoda ta daje identyczny wynik co pierwszy sposób, co niejako ją legitymizuje. W naszym przypadku owo ”wewnętrzne ”równanie ma postać
| (1.13) |
co po uproszczeniu daje
| (1.14) |
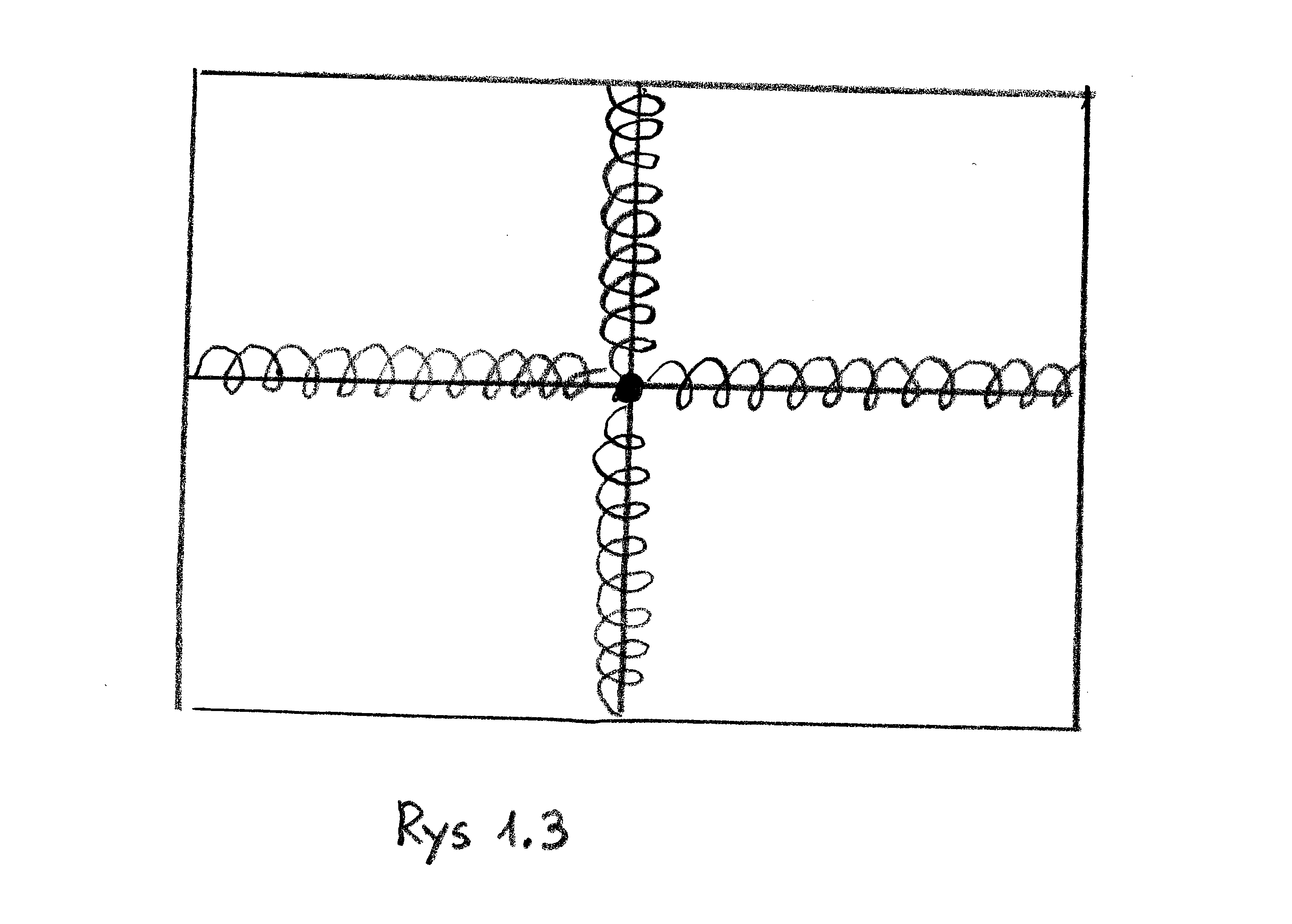
Przykład 1.6
Ruch drgający dwuwymiarowy
Za pomocą układu sprężyn, (jak na rysunku poniżej) możemy wykreować sytuację, w której wychyleniu w każdą możliwą stronę od punktu równowagi, towarzysz siła proporcjonalna do wychylenia lecz przeciwnie zorientowana, tzn. ściągająca ciało z powrotem do środka równowagi.
Umieszczając początek układu współrzędnych w punkcie równowagi, otrzymamy dwuwymiarową wersję Przykładu 1.4., gdzie ruch jest opisany równaniem wektorowym:
| (1.15) |
gdzie
| (1.16) |