Zagadnienia

11.1 Redukcja symplektyczna.
11.2 Pochodna Liego
11.3 Miary niezmiennicze dla potoków hamiltonowskich.
11.4 Algebraiczne tło mechaniki hamiltonowskiej.
11.5 Relacje komutacyjne.
11.6 Strukturalne spojrzenie na formalizm Hamiltona.

11. Miarowe, algebraiczne i strukturalne aspekty mechaniki Hamiltona.

11.1. Redukcja symplektyczna.

Symetryczna budowa równań Hamiltona umożliwia postępowanie redukujące liczbę równań i liczbę szukanych funkcji w sytuacji, kiedy jedna ze współrzędnych nie występuje explicite w funkcji Hamiltona (nazywamy ją wtedy współrzędną cykliczną). Niech $q_{i}$ będzie taką współrzędną. Wtedy $i-te$ ”pędowe” równanie jest postaci:

$\dot{p}_{i}=-\frac{\partial H}{\partial q_{i}}=0$

Zatem pęd $p_{i}$ pozostaje stały w czasie ruchu. Wstawiając jego stałą wartość $p^{0}_{i}$ do hamiltonianu, otrzymujemy układ równań z funkcją Hamiltona nie zawierająca $q_{i}$ ani $p_{i}$ a zatem układ 2n-2 równań (przy początkowej liczbie 2n równań). Po ich ewentualnym rozwiązaniu pozostaje jeszcze scałkować równanie:

$\dot{q}_{i}=\frac{\partial H}{\partial p_{i}}\big(q_{1}(t),...q_{n}(t),p_{1}(t),...\dot{p}_{i},...p_{n}(t)\big)=f(t)$

Wniosek 11.1

Układ o dwóch stopniach swobody (tj. dla n=2 ) i mający jedną współrzędną cykliczną, jest rozwiązalny w kwadraturach.

Niech $q_{1}$ będzie współrzędną cykliczną. Zgodnie z opisanym powyżej postępowaniem, redukujemy sytuację do układu

$\displaystyle{\dot{q}_{2}=\frac{\partial H}{\partial p_{2}},\dot{p}_{2}=-\frac{\partial H}{\partial q_{2}}}$

(11.1)

Układ ten ma całkę pierwszą $H\big(p_{1}^{0},p_{2}(t),q_{2}(t)\big)=c$ , która wyrażona za pomocą położeń i prędkości ma postać:

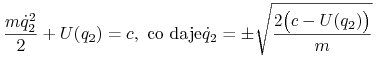$\displaystyle{\frac{m\dot{q}_{2}^{2}}{2}+U(q_{2})}=c,\textrm{ co daje}\dot{q}_{2}=\pm\displaystyle{\sqrt{\frac{2\big(c-U(q_{2})\big)}{m}}}$

a zatem zagadnienie rozwiązania naszego układu sprowadza się do wyznaczenia dwu całek.

∎

11.2. Pochodna Liego

Niech $X=(X_{1},..X_{n})$ będzie polem wektorowym klasy $C_{1}$ określonym na otwartym podzbiorze $\Omega\subset{\bf R}^{n}.$ Rozważmy układ równań z warunkiem początkowym

$\Bigg\{\begin{array}[]{ccc}\dot{y}(t)=X\big(y(t)\big)\\ y(0)=x\end{array}$

(11.2)

Z twierdzenia o istnieniu i jednoznaczności rozwiązań dla takiego układu wynika, że przy każdym warunku początkowym $x$ istnieje $\epsilon(x)>0$ oraz krzywa $\big(-\epsilon(x),\epsilon(x)\big)\ni t\rightarrow y_{x}(t)\in{\bf R}^{n},$ spełniająca (11.2). Ustalmy wartość $t$ i zmieniajmy warunek początkowy $x.$ Wtedy dla $x$ takich, że $|t|<\epsilon(x)$ jest dobrze określone odwzorowaniem $\varphi _{t}^{x}.$

$\varphi _{t}^{X}(x)=y_{x}(t)$

(11.3)

Z twierdzenia o gładkiej zależności rozwiązania (11.2) od warunków początkowych wynika, że odwzorowanie $\varphi _{t}$ jest różniczkowalne a z jednoznaczności rozwiązania zagadnienia (11.2) wynika, że jeżeli wszystkie elementy następującej formuły (11.4) są dobrze określone, to zachodzi równość:

$\displaystyle{\varphi _{{t_{1}+t_{2}}}^{X}(x)=\varphi _{{t_{1}}}^{X}\big(\varphi _{{t_{2}}}^{X}(x)}\big).$

(11.4)

Zatem (na być może mniejszym zbiorze) odwzorowanie $\varphi _{t}^{X}$ jest dyfeomorfizmem, na obraz tego zbioru - ”lokalnym dyfeomorfizmem”. W sytuacji, kiedy dla $t\in{\bf R}$ dana jest rodzina przekształceń określonych dla każdego $x\in\Omega$ i o wartościach w $\Omega$ a przy tym spełnione są warunki (11.4) oraz $\varphi _{0}=id_{\Omega},$ powiemy, że rodzina ${\bf R}\ni t\rightarrow\varphi _{t}$ jest jednoparametrową grupą odwzorowań $\Omega.$ Dla odwzorowań $\varphi _{t}^{X}$ definiowanych za pomocą (11.3) sytuacja jest bardziej złożona. Globalnie na $\Omega$ określone jest jedynie przekształcenie $\displaystyle{\varphi _{0}^{X}=id_{{{\bf R}^{n}}}}$ natomiast dla $t\neq 0$ każde przekształcenie $\varphi _{t}^{X}$ ma swoją dziedzinę. Dziedziny te rosną, kiedy $t\rightarrow 0$ oraz dla każdego $x\in{\bf R}^{n}$ istnieje $\epsilon(x),$ że dla $|t|<\epsilon(x)$ $x$ znajduje się w dziedzinie $\displaystyle{\varphi _{t}^{x}}.$ W tej sytuacji powiemy, że pole wektorowe $X$ określa lokalną grupę 1- parametrowa lokalnych dyfeomorfizmów $\Omega.$ Za pomoca tej grupy zdefiniujemy pochodną Liego pola tensorowego na $\Omega.$

Definicja 11.1

Niech $X$ będzie polem wektorowym klasy $C^{1}$ na otwartym podzbiorze $\Omega\subset{\bf R}^{n}.$ Niech $\{\varphi _{t}^{X}\} _{t}\in{\bf R}$ będzie lokalną 1-parametrowa grupą lokalnych dyfeomorfizmów $\Omega$ określoną przez $X.$ Niech $W$ będzie polem tensorowym walencji $(r,s)$ . Pochodną Liego pola $W$ wyznaczoną przez pole $X$ (oznaczaną $\mathcal{L}_{X}W$ ) nazwiemy pole tensorowe też o walencji $(r,s),$ którego wartość w punkcie $p$ otrzymujemy według następującej recepty realizowanej w dwóch krokach:

Krok 1
Tworzymy tensor $\widetilde{W}_{p}^{t},$ będący formą $(r+s)$ -liniową o argumentach $\xi _{i}\in T_{p}(\Omega)$ $i=1,..r$ oraz $\alpha _{j}\in T^{*}_{p}(\Omega)$ $j=1,..s$ przechodząc od $W_{{\varphi _{t}^{X}(p)}}$ do $\widetilde{W}_{t}^{p}$ zgodnie z formułą:

$\widetilde{W}^{t}_{p}(\xi _{1},..,\xi _{r},\alpha _{1},..,\alpha _{s})=$

$\displaystyle{=W_{{\varphi _{t}^{x}(p)}}\big(d_{p}\varphi _{t}^{x}(\xi _{1}),..,d_{p}\varphi _{t}^{x}(\xi _{r}\big),\alpha _{1}\circ d_{{p_{t}^{x}(p)}}\varphi _{t}^{x},..,\alpha _{s}\circ d_{{p_{t}^{x}(p)}}\varphi _{t}^{x}}\big).$

Krok 2
Wyznaczamy granicę

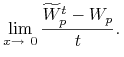$\lim _{{x\to\ 0}}\displaystyle{\frac{\widetilde{W}_{p}^{t}-W_{p}}{t}}.$

Czytelnika zainteresowanego poprawnością i zakresem stosowalności tej definicji odsyłamy do książek o geometrii różniczkowej. My poprzestaniemy na zacytowaniu kilku własności pochodnej Liego potrzebnych w dalszym tekście.

Stwierdzenie 11.1

Niech $X$ będzie polem wektorowym klasy $C^{1}$ na $\Omega\subset{\bf R}^{n}.$ Dla k-formy różniczkowej $\omega$ określmy zwężenie $X\rfloor\omega$ wzorem

$(X\rfloor\omega)(\xi _{1},..,\xi _{{k-1}})=\omega(X,\xi _{1},..,\xi _{{k-1}})$

Wtedy

$\displaystyle{\mathcal{L}_{X}\omega=X\rfloor d\omega+d(X\rfloor\omega)}$
$\displaystyle{d\circ\mathcal{L}_{X}=\mathcal{L}_{X}\circ d}$
$\displaystyle{\mathcal{L}_{X}f=Xf}\ \textrm{dla funkcji różniczkowalnej }\ f$
$\displaystyle{\mathcal{L}_{X}(Y)=[X,Y]}\ \textrm{dla pola wektorowego}\ Y$
$\displaystyle{[X,Y]\rfloor\eta=\mathcal{L}_{X}(Y\rfloor\eta)}$
$\displaystyle{\mathcal{L}_{X}\circ i_{Y}=i_{Y}\circ\mathcal{L}_{X}\ \textrm{gdzie}\ i_{Y}(\omega)=Y\rfloor\omega}$

11.3. Miary niezmiennicze dla potoków hamiltonowskich.

Niech $X=(X_{1},..,X_{n})$ będzie polem wektorowym klasy $C_{1}$ określonym na otwartym podzbiorze $\Omega\subset{\bf R}^{n}.$ Niech $\{\varphi _{t}^{X}\} _{{t\in{\bf R}}}$ będzie lokalną grupą lokalnych dyfeomorfizmów $\Omega$ określoną przez pole $X.$ Powiemy, że lokalny dyfeomorfizm $\varphi _{t}^{X}$ zachowuje miarę $\mu$ jeżeli

$\mu\big(\varphi _{t}^{X}(A)\big)=\mu(A)$

dla każdego otwartego $A\subset\Omega,$ dla którego $\varphi _{t}^{X}$ jest określony.

Diwergencją pola nazwiemy funkcję

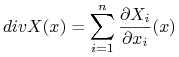$divX(x)=\displaystyle{\sum _{{i=1}}^{n}\frac{\partial X_{i}}{\partial x_{i}}(x)}$

Stwierdzenie 11.2

(Liouville) Jeżeli $divX=0$ to lokalne difeomorfizmy $\varphi _{t}^{X}$ związane z polem $X$ zachowują miarę Lebesque'a na $\Omega.$

Ponieważ $\dot{y}(t)=X\big(y(t)\big),$ korzystając z wzoru Taylora, dostaniemy

$\varphi _{t}^{X}(y)=y+X(y)\cdot t+0(t^{2}).$

Niech $D$ będzie otwartym zbiorem ograniczonym, takim że $\varphi _{t}^{X}$ jest określone dla $x\subset D.$ Oznaczając przez $volA$ miarę Lebesque'a zbioru $A,$ rozważmy funkcję $v(t)=vol\big(\varphi _{t}^{X}(D)\big).$ Wtedy

$\displaystyle{\frac{v(t+\triangle t)-v(t)}{\triangle t}=\frac{1}{\triangle t}\Big(vol\big(\varphi _{{\triangle t}}^{X}\big(\varphi _{{t}}^{X}(D)\big)\Big)-vol\varphi _{t}^{X}(D)\Big)}=$

$=\frac{1}{\triangle t}\int _{{\varphi _{t}^{X}(D)}}\Big(J\varphi _{{\triangle t}}^{X}(y)-1\Big)dy,$

gdzie $J\varphi _{{\triangle t}}^{X}(y)$ jest jakobianem przekształcenia $\varphi _{{\triangle t}}^{X}$ w punkcie $y\in\varphi _{t}^{X}(D).$ Ponieważ chcemy obliczyć granicę przy $\triangle t\rightarrow 0,$ zobaczymy jak zależy od $\triangle t$ wyrażenie $J\varphi _{{\triangle t}}^{X}(y).$ Ponieważ

$\varphi _{{\triangle t}}^{X}(y)=y+X(y)\cdot\triangle t+0\big((\triangle t)^{2}\big)$

macierz różniczki $d_{y}\varphi _{{\triangle t}}^{X}$ ma wyrazy

$a_{{ij}}=\delta _{j}^{i}+\frac{\partial X_{i}}{\partial y_{j}}(y)\cdot\triangle t+0\big((\triangle t)^{2}\big)$

a więc

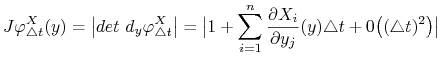$J\displaystyle{\varphi _{{\triangle t}}^{X}(y)}=\big|det\ d_{y}\varphi _{{\triangle t}}^{X}\big|=\big|1+\displaystyle{\sum _{{i=1}}^{n}\frac{\partial X_{i}}{\partial y_{j}}(y)}\triangle t+0\big((\triangle t)^{2}\big)\big|$

Z założenia, że $divX=0$ wynika więc, że $\frac{dv^{{\prime}}}{dt}=0,$ zatem $vol\varphi _{t}^{X}(D)=vol(D),$ dla każdego $t$ .

∎

Wniosek 11.2

Niech $M$ będzie rozmaitością symplektyczną wymiaru 2n i niech $(U,\varphi)$ będzie mapą symplektyczna na $M.$ Wtedy lokalne dyfeomorfizmy związane z polami hamiltonowskimi $grad_{\omega}F$ zachowują miarę Lebesque'a na $\varphi(U).$

Ponieważ zgodnie z (10.16)

$grad_{\omega}F=\displaystyle{\Big(\frac{\partial F}{\partial X_{{n+1}}},...,\frac{\partial F}{\partial X_{{2m}}},-\frac{\partial F}{\partial x_{1}},...,\frac{\partial F}{\partial x_{n}}}\Big)$

mamy $div(grad_{\omega}F)=0.$

∎

11.4. Algebraiczne tło mechaniki hamiltonowskiej.

Związek równań (10.19) z fizyką polega na dwóch założeniach.

- Po pierwsze - w przypadku ewolucji układu fizycznego, rozmaitość $M$ powinna być wiązką kostyczną do przestrzeni konfiguracyjnej naszego układu
- Po drugie - prawe strony rozważanych równań powinny być współrzędnymi gradientu symplektycznego funkcji $H$ równej całkowitej energii naszego układu, wyrażonej za pomocą pędów i położeń.
Abstrahując od takich fizycznych ograniczeń możemy rozważać układ o postaci:

$\dot{x}(t)=grad_{\omega}F(x)$

(11.5)

dla dowolnej rozmaitości symplektycznej $(M,\omega).$ (Zgodnie z Definicją 10.4 i wzorem (10.17) prawa strona w (11.5) jest zdefiniowana niezależnie od współrzędnych lokalnych na M). Następujące dalej obserwacje pokazują algebraiczne tło ewolucji opisywanej układem (11.5). Obecność tej struktury w tle mechaniki klasycznej była jedną ze wskazówek przy budowaniu formalizmu mechaniki kwantowej.

Definicja 11.2

Niech $M$ będzie 2m wymiarową rozmaitością symplektyczną z formą $\omega.$ Niech $C^{\infty}(M)$ będzie algebrą funkcji nieskończenie wiele razy różniczkowalnych o wartościach w ${\bf R}$ (lub w ${\bf C})$ na $M.$ Określmy operację

$C^{\infty}(M)\times C^{\infty}(M)\ni(f,g)\rightarrow\{ f,g\}\in C^{\infty}(M)$

(zwaną nawiasem Poissona ) za pomocą formuły

$\{ f,g\}=(grad_{\omega}f)\cdot g$

(11.6)

Stwierdzenie 11.3

(a) Nawias Poissona jest operacją dwuliniową i antysymetryczną.
(b) Dla $f,g,h,\in C^{\infty}(M)$ spełniona jest tożsamość Jacobiego.

$\{ f,\{ g,h\}\}+\{ g\{ h,f\}\}+\{ h,\{ f,g\}\}=0$

(11.7)

(Szkic) (a) Z formuły (10.18) widać, że (11.6) zależy liniowo od $f.$ Wynika z niej również opis lokalny nawiasu $\{ f,g\}$ w mapie symplektycznej:

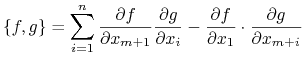$\{ f,g\}=\displaystyle{\sum _{{i=1}}^{{n}}\frac{\partial f}{\partial x_{{m+1}}}\frac{\partial g}{\partial x_{i}}-\frac{\partial f}{\partial x_{1}}\cdot\frac{\partial g}{\partial x_{{m+i}}}}$

(11.8)

Zatem $(grad_{\omega}f)g=(-grad_{\omega}g)f$ a więc nawias Poissona jest formą antysymetryczną.
(b) Wykorzystując antysymetrię nawiasu Poissona, przekształćmy (11.7) otrzymując:

$\{ f,\{ g,h\}\}-\{ g\{ f,h\}\}=\{\{ f,g\},h\}.$

Równość tę można odczytać jako równość

$grad_{\omega}f\Big((grad_{\omega}g)h\Big)-grad_{\omega}g\Big((grad_{\omega}f)h\Big)=\Big(grad_{\omega}\{ f,g\}\Big)h$

Ponieważ zachodzi ona przy dowolnym $h,$ traktując pola wektorowe jako operacje liniowe, możemy napisać

$\Big(grad_{\omega}f\Big)\circ\Big(grad_{\omega}g\Big)-\big(grad_{\omega}g\Big)\circ\Big(grad_{\omega}f\Big)=grad_{\omega}\{ f,g\}$

(11.9)

i oznaczając komutator tych operacji jako nawias Liego odpowiednich pól możemy (11.9) zapisać w postaci

$\Big[grad_{\omega}f,grad_{\omega}g\Big]=grad_{\omega}\{ f,g\}$

(11.10)

Przedstawione przejścia można też przeprowadzić w przeciwnym kierunku, co dowodzi, że równości (LABEL:10.4.3) i (11.10) są równoważne. Wykażemy, że zachodzi równość (11.10). W tym celu zastąpimy ją równoważną (ze względu na nieosobliwość $\omega$ ) równością

$\Big[grad_{\omega}f,grad_{\omega}g\Big]\rfloor\omega=(grad_{\omega}\{ f,g\})\rfloor\omega.$

(11.11)

Na mocy Stwierdzenia 11.1 punkty 5, 2, i 3 oraz równości (10.17) zapisanej w formie $\big(grad_{\omega}f\big)\rfloor\omega=df$ możemy lewą stronę (11.11) przedstawić w postaci

$\mathcal{L}_{{grad_{\omega}f}}(dg)-{\mathcal{L}_{{grad_{\omega}g}}(df)}=d\big((grad_{\omega}f)\big)\cdot g\big)=d\{ f,g\}$

Natomiast strona prawa przyjmuje postać $grad_{\omega}\{ f,g\}\rfloor\omega=d\{ f,g\}.$

∎

Uwaga 11.1

Punkty $(a)$ i $(b)$ Stwierdzenia 11.3 można podsumować mówiąc, że przestrzeń liniowa $C^{\infty}(M)$ wyposażona w dwuliniową operację

$C^{\infty}(M)\times C^{\infty}(M)\ni(f,g)\rightarrow\{ f,g\}\in C^{\infty}(M)$

jest algebrą Liego.Również przestrzeń liniowa $\Gamma^{\infty}(M)$ wszystkich pól wektorowych klasy $C^{\infty}$ na $M,$ wyposażona w nawias Liego jest algebrą Liego. Zauważmy, że z (11.10) wynika, że odwzorowanie

$grad_{\omega}:\big(C^{\infty}(M),\{\cdot,\cdot\}\big)\ni f\longrightarrow grad_{\omega}f\in\big(\Gamma^{\infty}(M),\big[\cdot,\cdot\big]\big)$

jest homomorfizmem tych algebr. Jako obraz tego homomorfizmu otrzymujemy zbiór wszystkich pól hamiltonowskich, który stanowi zatem algebrę Liego. Jądrem homomorfizmu $grad_{\omega}$ są funkcje stałe. Powyższa struktura algebry Liego jest związana z konkretnym układem mechanicznym uwzględniając jedynie jego przestrzeń konfiguracyjną.

Stwierdzenie 11.4

(Poisson)

Niech $M$ będzie rozmaitością symplektyczną z formą $\omega.$ Niech $H\in C^{\infty}(M).$ Rozpatrzmy ewolucję ${\bf R}\ni t\rightarrow x(t)\in M$ opisaną układem równań Hamiltona

$\dot{x}(t)=grad_{\omega}H\big(x(t)\big)$

(11.12)

Wtedy
(a) jeżeli $\{ f,H\}=0$ to $f$ jest całką pierwszą układu (11.12)
(b) jeżeli $f_{1}$ i $f_{2}$ są całkami pierwszymi tej ewolucji, to także $\{ f_{1},f_{2}\}$ jest całką pierwszą.

(a) Mamy

$\frac{d}{dt}f\big(x(t)\big)=\Big(grad_{\omega}H\big(x(t)\big)\Big)\cdot f=\{ H,f\}\big(x(t)\big)$

Zatem $f$ jest całką pierwszą wtedy i tylko wtedy, gdy $\{ f,H\}=0.$
(b) Z tożsamości Jacobiego (LABEL:0.3.3) wynika, że

$\{ H,\{ f_{1},f_{2}\}\}=\{ f_{1}\{ f_{2},H\}-\{ f_{2}\{ H,f_{1}\}\},$

ale $\{ f_{2},H\}=\{ H,f_{1}\}=0.$ Zatem $\{ H\{ f_{1},f_{2}\}\}=0,$ co należało pokazać.

∎

Uzupełnieniem poprzedniego stwierdzenia jest pochodzące od Emmy Noether.

Stwierdzenie 11.5

Niech będą dane dwa układy o postaci (11.5) i o prawych stronach równych $grad_{\omega}F_{i},i=1,2.$ Jeżeli 1-parametrowa grupa lokalna $t\rightarrow x_{t}^{1}$ związana z polem $grad_{\omega}F_{1}$ zachowuje $F_{2},$ to $F_{1}$ jest całką pierwszą układu $\dot{x}=grad_{\omega}F_{2}.$

Niech $x\in M$ i rozważmy krzywą całkową $x_{t}^{1}(x),$ gdzie $x_{0}^{1}=x$ wtedy

$F_{2}\big(x_{t}^{1}(x)\big)=F_{2}(x)=const$

a zatem

$\displaystyle{\big((grad_{\omega}F_{1})\cdot F_{2}\big)(x)=\frac{d}{dt}\arrowvert _{{t=0}}F_{2}\big(x_{t}^{1}\big)}=0$

czyli

$\{ F_{2},F_{1}\}(x)=0$

i ze Stwierdzenia 11.4 (a) wynika teza.

∎

11.5. Relacje komutacyjne.

Przy powstawaniu formalzmu mechaniki kwantowej ważną wskazówką były wartości nawiasu Poissona dla kilku podstawowych funkcji, jakimi są położenia $q_{1},...,q_{n}$ i pędy $p_{1},...,p_{2},$ będące współrzędnymi w wiązce kostycznej do przestrzeni konfiguracyjnej naszego układu. Dla mapy symplektycznej, w której nawias Poissona zadany jest formułą (11.12) otrzymamy

$\{ p_{i},p_{j}\}=0i,j,=1,...n$

(11.13)

Aby uzyskać (11.13) wystarczy w formule (11.12) przyjąć

$f=p_{i},g=p_{j},\ \textrm{oraz}\ (x_{1},...x_{n})=(q_{1},...q_{n})\ \ \textrm{i}(x_{{n+1}},...x_{{2n}})=(p_{1},...p_{n})\big).$

W analogiczny sposób otrzymamy

$\{ q_{i},q_{j}\}=0i,j=1,...n$

(11.14)

$\{ p_{i},q_{j}\}=-\delta _{j}^{i}{\bf 1}i,j=1,....$

(11.15)

gdzie ${\bf 1}$ oznacza funkcję stałą, przyjmującą wartość 1.

11.6. Strukturalne spojrzenie na formalizm Hamiltona.

Teoria zajmująca się opisem zmian w czasie układu fizycznego składa się na ogół z trzech części. Po pierwsze podaje matematyczny model rzeczywistości podlegającej ewolucji. Opis tej rzeczywistości w ustalonej chwili nazwiemy stanem układu w tej chwili.

Drugą częścią teorii - najważniejszą fizycznie - jest matematyczne sformułowanie prawa ewolucji. Najczęściej prawo takie jest opisane równaniem różniczkowym. Trzecim składnikiem teorii jest wyróżnienie elementów dających informację o stanach układu, które z jednej strony powinny taki stan wyznaczać, a z drugiej strony mogłyby być wyznaczane za pomocą obserwacji i doświadczeń.
Elementy takie nazwiemy obserwablami.

W hamiltonowskim ujęciu mechaniki, opisem rzeczywistości jest przestrzeń fazowa $\mathcal{F}$ układu. W najprostszym przypadku, układu n-punktów poruszających się swobodnie w ${\bf R}^{3},\mathcal{F}$ jest wiązką kostyczną do ${\bf R}^{{3n}}.$ Stanami naszego układu będą punkty $\mathcal{F}.$ Prawem opisującym ewolucję układu są równania Hamiltona, określone przez naturalną strukturę symplektyczną na $\mathcal{F}$ oraz przez funkcję Hamiltona $H=T+V,$ gdzie $T$ jest energia kinetyczną a $V$ potencjałem. We współrzędnych kartezjańskich równania te mają postać

$\dot{q}_{i}=\frac{\partial H}{\partial p_{i}}=\frac{p_{i}}{m_{i}}\\ \dot{p}_{i}=-\frac{\partial H}{\partial q_{i}}=-\frac{\partial V}{\partial q_{i}}=F_{i}(q)$

(11.16)

a ewolucja to przejście od stanu początkowego wyznaczającego warunki początkowe $q(t_{0})=q_{0}p(t_{0})=p_{0}$ do stanu w chwili $T$ wyznaczonego w wyniku rozwiązania układu (11.16). Obserwablami dla naszego układu będą funkcje na $\mathcal{F},$ takie, jak współrzędne, pędy, momenty pędu energia etc. Na równi z ewolucją obserwabli $q_{1},..q_{n},p_{1},..p_{n}$ daną równaniami (11.16) moglibyśmy badać bezpośrednio ewolucję innych obserwabli. I tak ewolucję obserwabli $B(q,p,t)$ możemy bezpośrednio opisać równaniem

$\displaystyle{\frac{\partial B(q,p,t)}{\partial t}=D_{H}\cdot B(q,p,t)}$

(11.17)

gdzie $D_{H}$ jest polem wektorowym na $\mathcal{F}$ o postaci

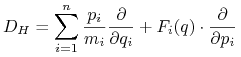$D_{H}=\displaystyle{\sum _{{i=1}}^{n}\frac{p_{i}}{m_{i}}\frac{\partial}{\partial q_{i}}+F_{i}(q)\cdot\frac{\partial}{\partial p_{i}}}$

Równanie to możemy interpretować jako równanie zwyczajne w przestrzeni funkcji na $\mathcal{F}.$ Istotnie pisząc $B_{t}(q,p)$ uzyskamy równanie opisujące krzywą
${\bf R}\ni t\rightarrow B_{t}$ w postaci

$\frac{dB_{t}}{dt}=D_{H}B_{t}$

gdzie $D_{H}$ jest operatorem liniowym $D_{H}(B_{t})=D_{H}\cdot B_{t}.$

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Matematyczne metody mechaniki