Zagadnienia

12.1 Uwagi ogólne.
12.2 Narodziny fizyki kwantowej
12.3 Powstawanie mechaniki kwantowej
12.4 Model Bohra atomu wodoru.

12. Mechanika kwantowa.

12.1. Uwagi ogólne.

Lata 1900 - 1930 były okresem zmian fizyce. Najważniejsze z nich to powstanie teorii względności oraz narodziny fizyki kwantowej. Jej podstawą jest mechanika kwantowa - nauka o zachowaniu atomów i cząstek elementarnych pod wpływem działajacych na nie sił.

Teoria względności stanowiła rewizję dotychczasowego systemu pojęć, była dziełem indywidualnym i w fazie powstawania niezależnym od fizyki eksperymentalnej. W odróżnieniu mechanika kwantowa dotyczyła nie znanych wcześniej aspektów rzeczywistości. Jej narodziny było procesem i wynikiem pracy wielu osób. Kolejne etapy tego procesu są związane ze znaczącymi odkryciami w teoriach elektromagnetyzmu, promieniotwórczości i cząstek elementarnych.

Główną trudnością, której pokonanie stanowi być może największe dokonanie dotychczasowej fizyki, było znalezienie właściwego modelowania matematycznego dla paradoksalnej i odległej od bezpośredniej inspekcji rzeczywistości świata mikro.

Inspiracja przy poszukiwaniu adekwatnego opisu pochodziła głównie z dwóch działów: mechaniki klasycznej i teorii elektromagnetyzmu Maxwella. W pierwszej z nich badanymi obiektami są ciała materialne, traktowane jako pojedyncze punkty lub ich sztywne układy. Ewolucja opisywana jest za pomocą równań różniczkowych zwyczajnych. Pociąga to implicite jej determinizm. Opisywane obiekty nie mogą się przenikać, co przy przyjętym modelowaniu nie wznosi znaczących trudności. Każdy obiekt zajmuje w dowolnej chwili ustalone miejsce w przestrzeni.

Modelowanie teorii elektromagnetyzmu różni się znacznie. Mamy tu do czynienia nie z poruszjącymi się punktami lecz ze zmieniającymi się w czasie polami wektorowymi. Ewolucja tych pól opisywana jest za pomocą układu równań różniczkowych cząstkowych. Jest także deterministyczna. Rozwiązaniem równań Maxwella sa (w niestacjonarnej sytuacji) fale elektromagnetyczne. Zajmują one całą rozważaną przestrzeń i mogą się przenikać (interferować).

12.2. Narodziny fizyki kwantowej

Nie ma sporu co do daty narodzin fizyki kwantowej. Jest nią 14 grudnia 1900r. W tym dniu Max Planck zaprezentował na posiedzeniu Niemieckiego Towarzystwa Fizycznego w Berlinie hipotezę porcjowego (czyli kwantowego) charakteru emisji fal elektromagnetycznych. Celem referatu było uzasadnienie fenomenologicznego wzoru na intensywnośc promieniowania ciała doskonale czarnego. Podana pół roku wcześniej także przez Plancka formuła (kolejna i najlepiej odpowiadająca doświadczeniom z ciągu wcześniej proponowanych) opisywała ilość emitowanej energii na jednostkę czasu i jednostkę powierzchni:

$e(\lambda,T)=a\lambda^{{-5}}\Big(\frac{1}{exp\frac{b}{k\lambda T}-1}\Big)$

(12.1)

gdzie $T$ jest temperaturą ciała, $\lambda$ długością emitowanej fali, k stałą Boltzmana, natomiast $a$ i $b$ stałymi o nieznanym znaczeniu fizycznym.

Przedstawione przez Plancka rozumowanie zakładło, że $e((\lambda,T)$ zmienia się skokowa w porcjach będących wielokrotnością najmniejszej możliwej porcji dla danej długości fali. Porcja taka jest wyrażona za pomocą częstości fali $\nu$ wzorem

$E=h\ \nu$

(12.2)

gdzie $h$ jest stałą uniwersalną ( stałą Plancka) mającą wymiar iloczynu jednostki pracy (1 Joul) mnożonej przez jednostkę czasu (1 sek). Potocznie $h$ jest nazywana kwantem działania.

W rezultacie Planck uzyskał teoretyczne potwierdzenie wzoru (12.1) a co więcej stałe $a$ i $b$ uzyskały interpretację fizyczną.

$a=8\pi\ hc\textrm{oraz }b=hc$

(12.3)

gdzie $c$ oznacza prędkość światła w próżni.

Uwzględniając (12.3) formuła (12.1) zestawiona w wynikiem doświadczalnym dla $e(\lambda,T)$ pozwala wyznaczyć stałą Plancka $h.$ Obecnie przyjmuje się $h=6,6260755\cdot 10^{{-34}}j\cdot sek$

Przymiotnikiem ”klasyczny” określa się obecnie całą teorię przedkwantową. Należą do niej np. mechanika klasyczna, elektrodynamika Maxwella, klasyczna mechanika statystyczna, termodynamika i teoria grawitacji.

Następnym potwierdzeniem kwantowej natury energii była praca Alberta Einsteina z 1905r. Zawierała ona koncepcyjną dyskusję kwantowego charakteru promieniowania elektromagnetycznego a w końcowym fragmencie pokazywała, jak przyjęcie hipotezy kwantowego charakteru energii pozwala wyjaśnić niezgodne z klasyczną elektrotermodynamiką cechy zjawiska fotoelektrycznego (tj. zjawiska wyzwalania stacjonarnych elektronów przez padające światło). Jedna z takich cech głosi, że natężenie prądu elektrycznego powstającego w fotokomórce zależy wprost proporcjonalnie od natężenia padającego na nią światła, natomiast energia indywidualnych elektronów od niego nie zależy.

Inne prace wczesnego okresu teorii kwantowej dotyczyły różnych niezgodności przewidywań klasycznych w odniesieniu do ciepła właściwego ciał, własności sieci krystalicznych itd.

Około roku 1911 świadomość sukcesu teorii kwantowej w wyjaśnianiu różnych aspektów drgań harmonicznych (pola elektromagnetycznego sieci krystalicznych) stała się powszechna.

12.3. Powstawanie mechaniki kwantowej

Impulsem, który przyspieszył powstanie mechaniki kwantowej był wynik doświadczenia Rutherforda, Geigera i Marsdena z 1909r. Wykazało ono w sposób nie pozostawiający wątpliwości, że atomy zawierają małe i ciężkie jądra. Po dwóch latach dalszych badań Rutherford zaproponował model planetarny atomów. Model ten w wielu aspektach odpowiadał wynikom doświadczeń rozproszeniowych, ale jego trwałość była niezgodna z klasyczną elektrodynamiką. Pomysł przezwyciężenia tego paradoksu za pomocą postulatów kwantowych pojawił się w 1913r. za sprawą duńskiego fizyka Nielsa Bohra.

Bohr zauważył, że planetarny model budowy atomu nie daje żadnej wskazówki co do jego rozmiarów. Na podstawie znajomości ładunków i mas nie można bowiem nic powiedzieć o odległościach. Potrzebna jest do tego jeszcze jedna wielkość wymiarowa, za którą Bohr przyjął stałą Plancka $h.$

Praca Bohra była oparta na następujących założeniach:

Energia promieniowania elektromagnetycznego nie jest wysyłana lub pochłaniana w sposób ciągły (zgodnie z klasyczną elektrodynamiką) ale jej wypromieniowanie następuje tylko przy przechodzeniu z jednego ”stanu stacjonarnego” do innego takiego stanu.
Dynamiczna równowaga układu w stanie stacjonarnym ustalana jest prawami mechaniki klasycznej. Przy przejściach między stanami stacjonarnymi prawa te nie obowiązują.
Przejściu od jednego stanu stacjonarnego do innego towarzyszy wysyłanie promieniowania o ustalonej częstości 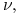$\nu,$ której związek z wypromieniowaną energią 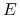$E$ dany jest wzorem Plancka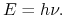 $E=h\nu.$
Dla układu składającego się z pojedynczego elektronu krążącego wokół jądra po orbicie kołowej, stan stacjonarny jest wyróżniony warunkiem, że moment pędu elektronu jest równy całkowitej wielokrotności 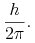$\displaystyle{\frac{h}{2\pi}}.$ Wśród wszystkich stanów stacjonarnych najważniejszy jest stan podstawowy, dla którego moment pędu jest równy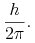 $\displaystyle{\frac{h}{2\pi}}.$

Jak już było powiedziane, doświadczenia rozproszeniowe (takie jak Rutherforda, Geigera i Marsdena z 1909r.) nie były w stanie obalić ani potwierdzić tych założeń.

W sukurs dalszemu rozwojowi fizyki przyszedł szczęśliwy przypadek związany z osobą Johannesa Balmera (1825 -1898). Miał on wykształcenie techniczne, pracował w Bazylei, ucząc arytmetyki i rysunku w wyższej szkole dla dziewcząt. Z zamiłowania był numerologiem, tj poszukiwaczem prawidłowości w układach liczb mających ”walor obiektywności”. Ponieważ tego typu układy są rzadkością, Balmer był wdzięczny koledze, który dostarczył mu ciąg czterech liczb $H_{\alpha},H_{\beta},H_{\gamma},H_{\delta},$ będących długościami fal ( w angstremach) dla linii widmowych wodoru. Pomiarami linii widmowych zajmowano się od czasu odkrycia przez Bunsena i Kirchhoffa, że stanowią one ”linie papilarne ” identyfikujące pierwiastek. Rozpoznaniem związków pomiędzy sprezentowanymi Balmerowi liczbami zajmowano się już dawniej, bez widocznego skutku. Balmer jednak odniósł błyskotliwy sukces. Zauważył mianowicie, że jeżeli każdą z przedstawionych mu liczb (widocznych w poniższej tabeli w kolumnie ”pomiar”), podzieli się przez ”liczbę bazową”
b = 3645,6, to otrzyma się z dużą dokładnością niewielkie ułamki.

Linia	Pomiar	Ze wzoru	Różnica
$H_{\alpha}$	6562.10	6562.08	+0,02
$H_{\beta}$	4860.74	4860.8	-0.06
$H_{\gamma}$	4340.1	4340,0	+0.1
$H_{\delta}$	4101.2	4101.3	-0,1

Konkretnie, liczby w kolumnie ”Ze wzoru” możemy przedstawić w formie:

$b\cdot\frac{9}{5},b\cdot\frac{4}{3},b\cdot\frac{25}{21},b\cdot\frac{9}{8}.$

Następnie Balmer zauważył, że powyższe liczby można też zapisać jako:

$b\cdot\frac{9}{5},b\cdot\frac{16}{12},b\cdot\frac{25}{21},b\cdot\frac{36}{32},$

co już sugeruje prawidłowość.

$b\cdot\displaystyle{\frac{n^{2}}{n^{2}-k^{2}}}\qquad\textrm{dla}\qquad k=2\qquad\textrm{oraz}\qquad n=3,4,5,6$

(12.4)

Dokładność opisu danych doświadczalnych za pomocą wzoru Balmera (12.4) nie pozostawia wątpliwości, że zgodność ta nie jest dziełem przypadku. Odkrycie Balmera stało się początkiem rewolucji w opisie linii widmowych i doprowadziło do powstania empirycznej zasady Rydyberga - Ritza, według której częstości linii widmowych dają się przedstawić jako różnice:

$\displaystyle{\nu=\frac{K}{(k+\alpha _{r})^{2}}-\frac{K}{(n+\alpha _{s})^{2}}}$

(12.5)

gdzie $n,k$ są liczbami naturalnymi a $K,\alpha _{r},\alpha _{s},$ stałymi zależnymi tylko od pierwiastka i serii widmowej.

Dla atomu wodoru i dla serii Balmera we wzorze (12.5) należy przyjąć $K=\frac{R}{h}\ \ ,\alpha _{r}=\alpha _{s}=0,\, k=2,\textrm{oraz}n=3,4,5,6.$ Otrzymujemy wtedy

$\nu _{n}=\frac{R}{\hbar}\displaystyle{\big(\frac{1}{2^{2}}-\frac{1}{n^{2}}\big)}n=3,4,5,6$

(12.6)

gdzie $R$ jest stałą Rydyberga, $\hbar=\frac{h}{2\pi}$ a $h$ jest stałą Plancka.

12.4. Model Bohra atomu wodoru.

Atom wodoru (według modelu planetarnego Rutherforda ) składa się z jądra o dodatnim ładunku $+e$ i obiegajacego go elektronu o ładunku $-e.$ Elektron jest przyciągany przez jądro siłą Coulomba o potencjale

$\displaystyle{U(r)=-\frac{e^{2}}{4\pi\epsilon _{0}}\ \ \frac{1}{r}}$

(12.7)

gdzie $\epsilon _{0}$ jest stałą dielektryczną próżni. Zgodnie ze Stwierdzeniem 5.4 zmiana promienia r odbywa się jak w ruchu 1-wymiarowym z potencjałem zredukowanym

$V(r)=\displaystyle{-\frac{e^{2}}{4\pi\epsilon _{0}}\frac{1}{r}}+\displaystyle{\frac{M^{2}}{2mr^{2}}}$

gdzie M jest stałym w czasie ruchu momentem pędu.

Przyjmiemy, że stan podstawowy odpowiada wartości $r,$ dla której $V(r)$ ma minimum, a zatem wtedy kiedy

$V^{{\prime}}(r)=\frac{e^{2}}{4\pi\epsilon _{0}r^{2}}-\frac{M^{2}}{mr^{3}}=0,$

skąd

$\displaystyle{r=\frac{4\pi\epsilon _{0}M^{2}}{me^{2}}}$

W modelu Bohra przyjmuje się, że dla stanu podstawowego ma być $M=\hbar,$ otrzymujemy stąd wzór na promień $a_{1}$ orbity stanu podstawowego

$\displaystyle{a_{1}=\frac{4\pi\epsilon _{0}\hbar^{2}}{me^{2}}}.$

(12.8)

Dla n-tego stanu stacjonarnego otrzymamy analogicznie, przyjmując wartość $M_{n}=n\hbar$

$\displaystyle{a_{n}=\frac{4\pi\epsilon _{0}n^{2}\hbar^{2}}{me^{2}}}.$

Energię $E_{n}$ na $n-$ tej orbicie wyznaczymy ze wzoru:

$E_{n}=\displaystyle{\frac{|p_{n}|^{2}}{2m}+U(a_{n})}.$

Zauważmy, że z uwagi na kołowość n-tej orbity mamy:

$|M_{n}|=|p_{n}|\cdot a_{n}$

skąd

$|p_{n}|=\frac{n\hbar}{a_{n}}=\frac{me^{2}}{4\pi\epsilon _{0}\hbar}\cdot\frac{1}{n}$

zatem

$\displaystyle{E_{n}=\frac{me^{4}}{32\pi^{2}\epsilon _{0}^{2}\hbar^{2}}\cdot\frac{1}{n^{2}}-\frac{e^{4}}{4\pi\epsilon _{0}}\cdot\frac{me^{2}}{4\pi\epsilon _{0}n^{2}h^{2}}}=$

$=-\frac{me^{4}}{32\pi^{2}\epsilon _{0}^{2}h^{2}}\cdot\frac{1}{n^{2}}n=1,2,...$

Wielkość $\displaystyle{\frac{me^{4}}{32\pi^{2}\epsilon _{0}^{2}\hbar^{2}}}$ nosi nazwę stałej Rydyberga, ma wymiar energii i jest oznaczana literą $R.$ Wygodne jest przyjąć $R$ jako jednostkę energii odpowiednią dla świata atomowego.

Zatem energia całkowita elektronu znajdującego się na n-tej orbicie Bohra wyróżnionej warunkiem $M=n\hbar$ wynosi

$E_{n}=-\frac{R}{n^{2}}n=1,2,...$

(12.9)

Uwzględniając wzór Plancka $E=\nu h$ otrzymamy stąd częstotliwość promieniowania emitowanego przy przejściu z $n-tej$ na $k-$ tą orbitę dla $n>k$ (tj. dla $E_{n}>E_{k}$ ). (Porównaj (12.6)).

$\displaystyle{\nu _{{n,k}}}=\displaystyle{\frac{E_{n}-E_{k}}{h}}=\displaystyle{\frac{R}{h}\Big(\frac{1}{k^{2}}-\frac{1}{n^{2}}}\Big)$

(12.10)

Okazuje się więc, że częstotliwości dla serii Balmera odpowiadają spadaniu na drugą orbiteę Bohra.

Dalszy rozwój teorii Bohra zmierzał do objęcia podobnym schematem bardziej skomplikowanych atomów i polegał na poszukiwaniu ogólniejszych postaci warunków kwantowych, które można by wtedy stosować.

Warunki te, których nie będziemy omawiać, znane są pod nazwą waunków Bohra - Sommerfelda. Znalazły one różne zastosowania, mi.in. do wyznaczania poziomów energetycznych atomu wodoru z uwzględnieniem dynamiki relatywistycznej.

Okres tych poszukiwań, zwany starszą teorią kwantów, nie przyniósł ostatecznego sformułowania mechaniki kwantowej. Ośrodkiem badań nad starszą teorią kwantów stał się Instytut Fizyki w Kopenhadze, stworzony dla Bohra przez rząd duński. Do dziś istnieje pojęcie ”kopenhaskiej interpretacji” mechaniki kwantowej, z którą związane są dwie zasady:

Zasada odpowiedniości, mówiąca, że dla dużych liczb kwantowych prawa mechaniki kwantowej powinny być prawie zgodne z prawami mechaniki klasycznej.

Drugą jest zasada komplementarności, mówiąca że opis zjawisk atomowych powinien być możliwy w dwóch modelach - korpuskularnym i falowym.

Zanim przejdziemy do rewolucji lat dwudziestych XX wieku, która przyniosła ostateczną formę mechaniki kwantowej, opiszemy fikcyjne doświadczenie pomysłu R. Feynmana, ukazujące problem z modelowaniem zjawisk kwantowych.

Opisane poniżej doświadczenie jest zachowującą istotę rzeczy alegorią rzeczywistych eksperymentów. Wnioski z nich stanowią istotną przesłankę dla konstrukcji formalizmu mechaniki kwantowej.

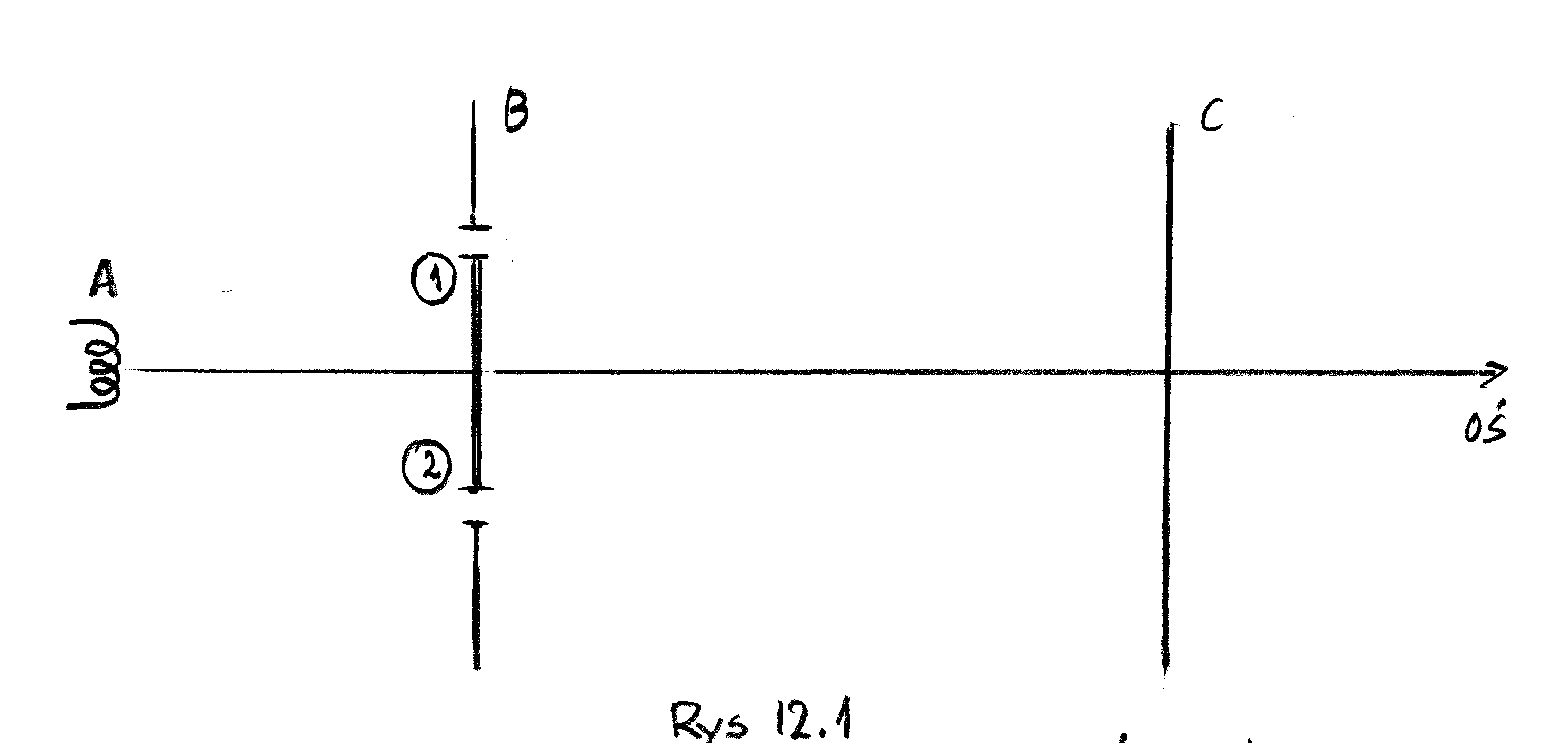
Doświadczenie dotyczy elektronów, których źródło znajduje się w punkcie A (zobacz rysunek 12.1). W pewnej odległości od A znajduje się przesłona B, w której są otwory, przez które elektrony mogą się przedostawać w kierunku ekranu C. Za pomocą urządzenia rejestrującego możemy obserwować pojawienie się elektronu, w postaci pojedynczego impulsu.

W wyniku wielokrotnych prób można więc ustalić z jaką częstością (z jakim prawdopodobieństwem ) elektrony pojawiają się się w danym miejscu ekranu C przy ustalonej konfiguracji otworów w przesłonie B.

Przeprowadzimy trzy eksperymenty, działając w opisany wyżej sposób przy trzech różnych konfiguracjach otworów.

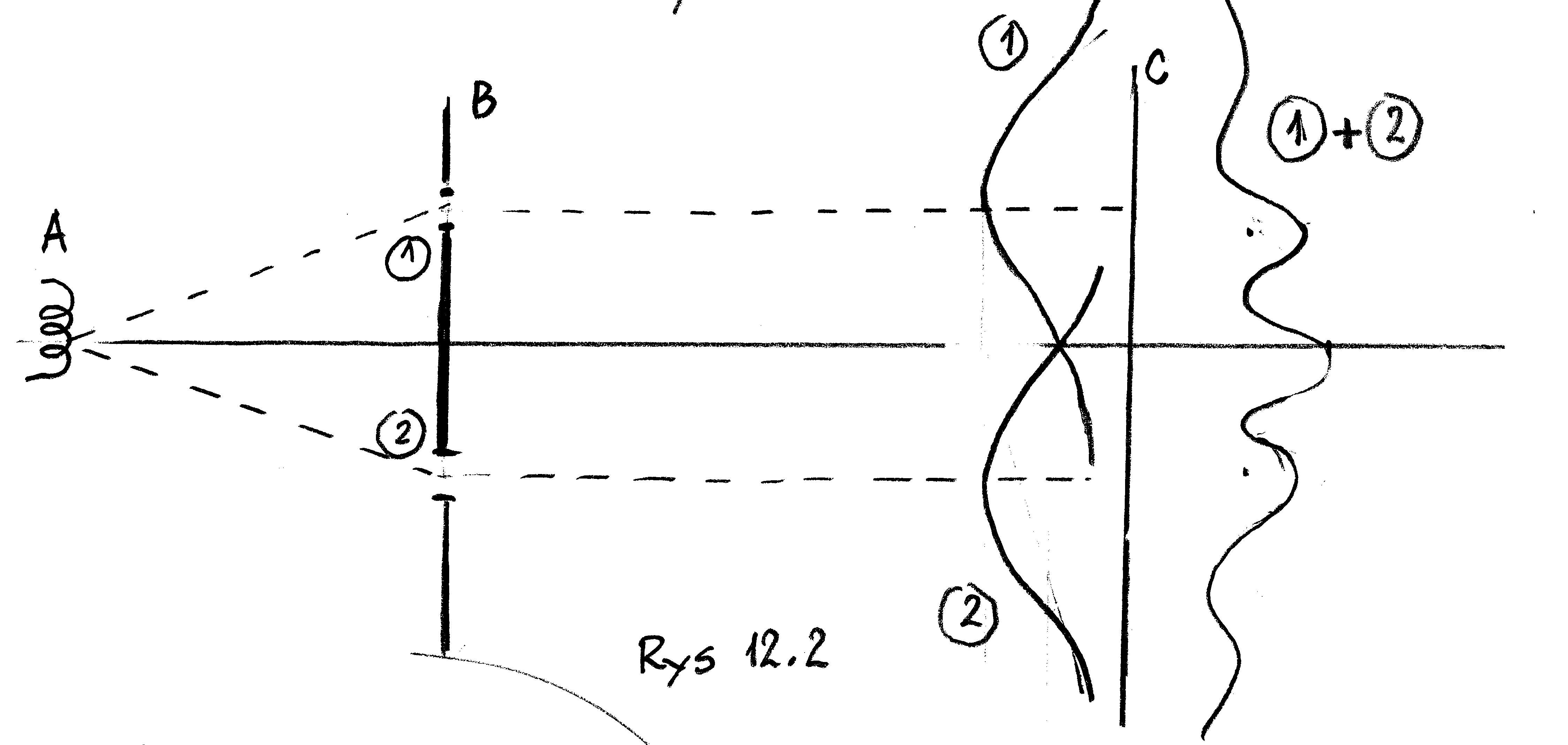
W pierwszym eksperymencie otwarty jest tylko otwór 1, w drugim tylko otwór 2 a w trzecim otwarte są oba otwory. Otóż okazuje się, że tak przeprowadzone trzy doświadczenia dają prawdopodobieństwo znalezienia się elektronu na ekranie C, opisane przez gęstości prawdopodobieństwa $f_{1},f_{2},f_{3},$ jak na rysunku poniżej:

gdzie rysunek (1) odpowiada sytuacji doświadczenia 1 itd. Zastanówmy się, co to oznacza. Przyjmując dla uproszczenia, że otwory 1 i 2 umieszczone są symetrycznie względem osi $0_{x},$ możemy przyjąć, że częstości trafiania elektronu w każdy z otworów są takie same. Wobec tego, przy otwartych obu otworach połowa elektronów będzie zachowywać się zgodnie ze statystyką $f_{1}$ a druga połowa zgodnie z $f_{2}.$ W rezultacie statystyka łączna $F$ miałaby postać

$F=\frac{1}{2}(f_{1}+f_{2})\neq f_{3}.$

Narzuca się tu porównanie sytuacji z falami na wodzie.

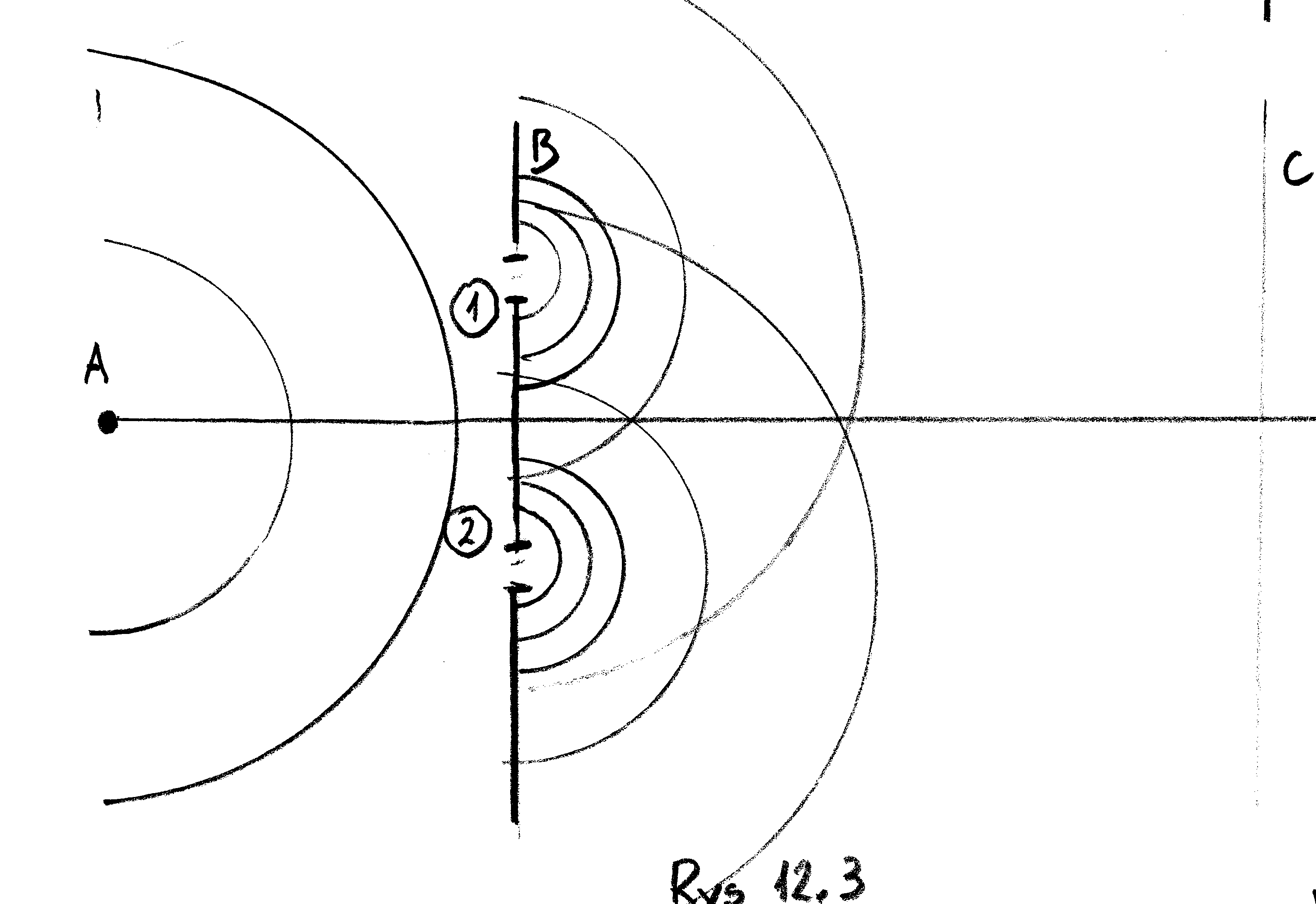
Wtedy, traktując elektron jako falę kulistą o środku w $A$ po jej dojściu do otworów 1 i 2, staje się ona (zgodnie z zasadą Huygensa) źródłem nowych fal kulistych. Fale te następnie interferują, wzmacniając się lub osłabiając, co doprowadza do sytuacji (1) + (2) na ekranie C.

Mamy tu więc sytuację, że wprawdzie elektron na ekranie C sygnalizuje swoje pojawienie się w ustalonym jego miejscu, ale jednocześnie, mając otwarte oba otwory w przesłonie, korzysta z obu z nich.

Eksperyment ten sugeruje następującą interpretację

Położenie elektronu daje się ustalić doświadczalnie, ale nie daje się przewidzieć w sposób pewny. To co możemy powiedzieć o jego przyszłym położeniu to tylko prawdopodobieństwo znalezienia się w pewnym obszarze.
Prawdopodobieństwo znalezienia się w stanie C, jeżeli wiemy że był on poprzednio w stanie B, nie jest otrzymywane jako prawdopodobieństwo warunkowe.

Przytoczone doświadczenie sugeruje, że opisywane przejście od stanu B do ostatecznego rozkładu na ekranie C nie produkuje ostatecznego prawdopodobieństwa $f_{3}$ w postaci $\frac{1}{2}f_{1}+\frac{1}{2}f_{2}$ . Elektron bowiem przebywa w punkcie 1 z prawdopodobieństwem 1/2 i w punkcie 2 też z prawdopodobieństwem 1/2.

Okazuje się (nie wynika to z jakościowego opisu $f_{3},$ ) że właściwym modelowaniem jest rozważanie funkcji o wartościach zespolonych, dla których $f_{1},f_{2}if_{3}$ są ich wartościami bezwzględnymi. To znaczy, że należy rozważyć