Zagadnienia

13.1 Fale materii de Broglie'a.
13.2 Równanie Schrödingera.
13.3 Równanie Schrödingera bez czasu.

13. Równanie Schrödingera

13.1. Fale materii de Broglie'a.

Rok 1926 można uważać za początek współczesnej mechaniki kwantowej. Pierwszą jaskółką nowych czasów była praca Heisenberga z lata 1925r. W niej to pojawiła się po raz pierwszy idea, że położenie i pęd powinny być opisywane wielkościami nieprzemiennymi, przy czym stała Plancka jest miarą ich nieprzemienności. Od tej pory zaczął się utrwalać pogląd, że przejście od mechaniki klasycznej do kwantowej (tzw. kwantowanie) polega na zastąpieniu - z zachowaniem pewnych reguł - klasycznych przemiennych obserwabli (por. (11.6)) nieprzemiennymi operatorami.

Zrozumienie matematyki, która stoi za tym przejściem, przychodziło stopniowo i dziś oryginalne prace z okresu tzw. mechaniki macierzowej (Heisenberg, Bohr, Jordan, Dirac) są zupełnie nieczytelne.

Mechanika macierzowa odniosła szereg sukcesów, rozpracowując kwantowy odpowiednik oscylatora harmonicznego (Heisenberg, Dirac) oraz, potwierdzając nowymi metodami, wzór Balmera - Bohra (12.10) (Pauli, Dirac). Słabą jej stroną był brak opisu ewolucji, (np. układów rozproszeniowych) oraz ogromne trudności rachunkowe.

Przełom nastąpił w wyniku połączenia mechaniki macierzowej z mechaniką falową de Broglie'a - Schrödingera.

W 1924r. L. de Broglie w swojej pracy doktorskiej przyjął jako założenie istnienie pewnego periodycznego zjawiska związanego z ruchem każdej porcji materii. Założył on, że cząstkom swobodnym (tj. punktom materialnym, pozostającym w polu stałego potencjału), których ruch ( z dokładnością do położenia początkowego) jest scharakteryzowany przez energię całkowitą $E$ i pęd $p,$ odpowiadają zespolone fale płaskie. tj funkcje

${\bf R}^{3}\times{\bf R}\ni(x,t)\rightarrow\psi(x,t)=A\cdot e^{{2\pi i(<k,x>-\nu t)}}\in{\bf C}$

(13.1)

gdzie $k\in{\bf R}^{3}$ jest wektorem a $\nu\in{\bf R}$ liczbą.

Wektor $k$ występuje we wzorze (13.1.1) wyznaczając formę liniową i wobec tego ewolucja wszystkich wektorów, dla których $<x,k>$ ma ustaloną wartość ( tj. leżących na ustalonej płaszczyźnie, będącej translacją płaszczyzny

$p=\{ x:<x,k>=0\}$

przebiega podobnie - stąd nazwa ”fala płaska ”.

Stała $A$ - amplituda fali $\Psi$ - ma w naszych rozważaniach znaczenie drugorzędne, podobnie jak położenie początkowe punktu materialnego, odpowiadającego fali $\Psi.$

Odpowiedniość de Broglie'a polega na przyporządkowaniu parze $(p,E)$ , gdzie $p$ jest pędem a $E$ energią całkowitą cząstki swobodnej pary $(k,\nu)$ , wyznaczającej falę płaską z dokładnością do amplitudy $A.$ Przyjmujemy wtedy

$\nu=\displaystyle\frac{E}{h},\ \ \ k=\frac{p}{h},$

(13.2)

gdzie $h$ jest stałą Plancka.

Oznaczmy dla wygody $\hbar=\displaystyle{\frac{h}{2\pi}}.$ Wtedy (13.1) i (13.2) dają:

$\Psi(x,t)=\displaystyle{A\cdot e^{{\frac{i}{\hbar}\big(\left\langle p,x\right\rangle-Et\big)}}}$

(13.3)

Niech $p=(p_{1},p_{2},p_{3})$ i przyjmijmy

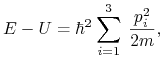$E-U=\hbar^{2}\:\displaystyle{\sum _{{i=1}}^{3}\:\frac{p_{i}^{2}}{2m}},$

gdzie $m$ jest masą cząstki.

Stwierdzenie 13.1

Funkcja (13.3) spełnia równanie falowe o postaci

$\Big(\displaystyle{\frac{E-U}{E^{2}}}\Big)\:\displaystyle{\frac{\partial^{2}\Psi}{\partial t^{2}}=\frac{1}{2m}}\bigtriangleup\Psi,$

(13.4)

$\textrm{gdzie}\;\bigtriangleup=\frac{\partial^{2}}{\partial x_{1}^{2}}+\frac{\partial^{2}}{\partial x_{2}^{2}}+\frac{\partial^{2}}{\partial x_{3}^{2}}\ \ \textrm{jest operatorem Laplace'a}.$

Dowód polega na policzeniu pochodnych funkcji $\Psi$ i nie będziemy go przytaczać.

13.2. Równanie Schrödingera.

Pokażmy teraz, jak od równania falowego i fal płaskich można przejść do zmodyfikowanej sytuacji - równania Schrödingera i fal prawdopodobieństwa.

Zauważmy najpierw, że poza geometryczną cechą płaskości, fale (13.3) są wyróżnione tym, że mają postać iloczynu funkcji zależnej od $x$ i funkcji zależnej od $t.$ Istotnie,

$\Psi(x,t)=\displaystyle{e^{{\frac{i}{\hbar}<k,x>}}}\cdot\displaystyle{{e^{{-\frac{i}{\hbar}Et}}}}$

Postąpmy o krok dalej i rozważmy ogólniejsze funkcje

$\varphi(x,t)=A(x)\cdot\displaystyle{e^{{-\frac{i}{\hbar}Et}}}$

(13.5)

gdzie $A$ jest funkcją zespoloną, na którą następnie narzucimy warunki wynikające z probalistycznej interpretacji opisywanej sytuacji.

Rozważmy także równanie

$\Big(\displaystyle{\frac{E-U}{E^{2}}}\Big)\ \displaystyle{\frac{\partial^{2}\Psi}{\partial t^{2}}=\frac{1}{2m}}\ \bigtriangleup\Psi,$

(13.6)

które formalnie wygląda, jak równanie (13.4), ale tym razem $E$ jest liczbą (poziomem energii całkowitej) natomiast $U$ jest funkcją rzeczywistą (potencjałem) na ${\bf R}^{3}.$

Rozważmy przestrzeń $L^{2}({\bf R}^{3})$ funkcji o wartościach zespolonych, określonych na ${\bf R}^{3},$ takich, że

$\displaystyle{\int _{{{\bf R}^{3}}}\arrowvert\ f(x)\ \arrowvert\ \ dx<+\infty}.$

(13.7)

W związku ze zmodyfikowanym równaniem (13.6) wprowadzimy operator (nieograniczony) działający na przestrzeni $L^{2}({\bf R}^{3})$ ”operator energii” $H$ za pomocą wzoru:

$Hf=\Big(\displaystyle{-\frac{\hbar^{2}}{2m}}\ \bigtriangleup+\ U\Big)f$

(13.8)

Stwierdzenie 13.2

Niech $\varphi$ będzie określona wzorem (13.5). Następujące warunki są równoważne

(a) $\varphi$ spełnia równanie (13.6),

(b) $HA=EA$

$\displaystyle{i\hbar\ \frac{\partial\varphi}{\partial t}}=H\varphi$

(13.9)

(a) $\Rightarrow$ (b). Jeżeli $\varphi(x,t)=A(x)\displaystyle{e^{{-\frac{i}{\hbar}Et}}}$ to po wstawieniu $\varphi$ do równania (13.6) otrzymamy

$\displaystyle{\frac{E-U}{E^{2}}\cdot\Big(-\frac{E^{2}}{\hbar^{2}}\ A(x)\ e^{{-\frac{i}{\hbar}Et}}\Big)=e^{{-\frac{i}{\hbar}Et}}\cdot\bigtriangleup\big(A\big)(x)}$

i upraszczając czynnik $\displaystyle{e^{{-\frac{i}{\hbar}Et}}}$ otrzymamy

$-(E-U)A(x)=\hbar^{2}\big(\bigtriangleup A\big)(x)$

skąd

$-EA(x)=\big(\hbar^{2}\bigtriangleup-U\big)A(x)$

czyli

$HA=EA$

(b) $\Rightarrow$ (a) Wszystkie przejścia poprzedniego dowodu można przeprowadzić też w przeciwnym kierunku.

$i\hbar\ \displaystyle{\frac{\partial\varphi}{\partial t}}=\big(\frac{\hbar^{2}}{2m}\bigtriangleup+U\big)\varphi.$

Wtedy

$i\hbar\ \displaystyle{\frac{d\alpha}{dt}\cdot A(x)t=\alpha(t)\ H(a)(x)}$

czyli dla tych $t,$ dla których $\alpha(t)\neq 0$

$\displaystyle{i\hbar\ \frac{d\alpha}{dt}\cdot\frac{1}{\alpha}=\frac{H(A)(x)}{A(x)}}$

Ponieważ lewa strona zależy od $t$ a prawa od $x,$ musi istnieć stała $E,$ dla której

$\displaystyle{i\hbar\ \frac{d\alpha}{dt}\cdot\frac{i}{\alpha}=E=\frac{H(A)(x)}{A(x)}}.$

Z równości tej wynikają dwa związki:

$\frac{d\alpha}{dt}=-\frac{i}{\hbar}E\ \ \ \textrm{oraz}\ \ H(A)(x)=E\cdot A(x)$

Z pierwszego wynika postać $\displaystyle{\alpha(t)=C\cdot e^{{-\frac{1}{\hbar}Et}}}$ a drugi jest identyczny z warunkiem (b):

(b) $\Rightarrow$ (c). Jeżeli $HA=EH$ to dla to dla $\varphi(x,t)=A(x)\displaystyle{e^{{-\frac{1}{\hbar Et}}}}$ zachodzi

$i\hbar\displaystyle{\frac{\partial\varphi}{\partial t}=EA(x){e^{{-\frac{1}{\hbar Et}}}}}=E\cdot\varphi=H\varphi,\ \textrm{co oznacza (c).}$

∎

Definicja 13.1

Równanie (13.9) nazywa się (pełnym) równaniem Schrödingera.
Warunek $Hf=Ef,$ czyli

$\Big(\displaystyle{-\frac{\hbar^{2}}{2m}}\bigtriangleup+U\Big)f=Ef$

(13.10)

nazywa się równaniem Schrödingera bez czasu.

Uwaga 13.1

Pokazane przez nas przejście: równanie falowe (13.4) i fale płaskie $\Rightarrow$ , równanie (13.6) i fale $\varphi(x,t)=A(x)\cdot\displaystyle{e^{{-\frac{i}{\hbar}E(t)}}}\Rightarrow$ równanie $HA=EA$ i równanie Schrödingera $i\hbar\ \displaystyle{\frac{\partial\varphi}{\partial t}}=H\varphi$ ujawniają związek między falami płaskimi i falami (13.5). Nie jest to jednak droga, na jakiej Schrödinger doszedł do sformułowania równań (13.9) i (13.10).

Pokazane przejścia są oparte na założeniu, że rozważane przez nas funkcje mają postać

$\varphi(x,t)=A(x)\cdot\alpha(t),$

(13.11)

co nie jest regułą dla rozwiązań dyskutowanych równań. (Równania są liniowe, więc np. suma rozwiązań o postaci (13.11) jest też rozwiązaniem). Jak pokazuje równoważność (b) $\Longleftrightarrow$ (c) w Stwierdzeniu 13.2, rozwiązania tej postaci odpowiają stanom stacjonarnym, to jest takim, kiedy amplituda $A$ funkcji $\varphi$ jest funkcją własną operatora energii $H.$

Uwaga 13.2

Erwin Schrödinger wprowadzając w 1926r. równania (13.9) i (13.10) nie miał jasnej interpretacji fizycznej ich rozwiązań. Interpretację taką podał wkrótce potem Max Born. Przyjął on, że rozwiązanie $\psi(t,x)$ równania Schrödingera (13.9) mające tę własność, że dla każdego ustalonego $t$ funkcja $F_{t}(x)=\psi(t,x)$ należy do $L^{2}({\bf R}^{3},dx),$ można interpretować jako ewolucję w czasie rozkładu prawdopodobieństwa. Wtedy $\int _{M}|\psi(t,x)|^{2}dx$ ma interpretację prawdopodobieństwa zdarzenia, że cząstka (lub układ cząstek) znajduje się w chwili $t$ w podzbiorze M przestrzeni konfiguracyjnej ${\bf R}^{3}$ lub ${\bf R}^{{3n}}$ . Okazuje się, że spełnienie warunku $\psi(t,x)\ni L^{2}({\bf R}^{3},dx)$ dla pewnego $t$ pociąga spełnienie analogicznego warunku także dla pozostałych $t,$ co uzasadnia traktowanie równania (13.9) jako równania zwyczajnego

$\frac{d}{dt}F_{t}=-\frac{i}{\hbar}HF_{t}$

w $L^{2}({\bf R}^{3},dx)$ i wiąże równanie Schrödingera z teorią jednoparametrowych grup unitarnych w przestrzeni Hilberta.

Interpretacja Borna oznacza, że wprawdzie położenie indywidualnej cząstki nie jest przewidywalne, ale ewolucja rozkładu prawdopodobieństwa tego położenia jest w pełni deterministyczna.

13.3. Równanie Schrödingera bez czasu.

Przy przejściu od mechaniki klasycznej do kwantowej operator występujący po prawej stronie równania (13.9), odpowiada funkcji Hamiltona układu. Stąd jego nazwa - operator energii. Jak wiemy, jedną z podstawowych cech natury jest występowanie energii w porcjach. Ponieważ są one niezmiernie małe, cecha ta nie ingeruje w formaliźmie dotyczącym zjawisk w skali makro. Staje się natomiast jednym z głównych czynników kształtujących opis w skali atomowej. Aby uzyskać porcjowy charakter obserwowanych wartości energii, zmienimy nasze myślenie o obserwablach. Realizujemy je jako operatory, których widmo jest związane z obserwowanymi wartościami np. energią. Pełny opis kwantyzacji polegający na zastąpieniu klasycznych obserwabli - funkcji na przestrzeni fazowej - ich odpowiednikami kwantowymi - operatorami w przestrzeni Hilberta - jest poza możliwościami aktualnej prezentacji.

Zamiast tego pokażemy, że zbiór wartości własnych operatora energii dla potencjału odpowiadającego atomowi wodoru jest istotnie dyskretny i jego wartości zgadzają się z poziomami energetycznymi orbit odpowiadających stanom stacjonarnym modelu Bohra.

Stwierdzenie 13.3

Niech $\lambda$ będzie wartością własną operatora $H$ tj.

$\Big(\displaystyle{-\frac{\hbar^{2}}{2m}}\bigtriangleup+U\Big)f=\lambda f,$

(13.12)

gdzie $f\in L^{2}({\bf R}^{3},dx)\textrm{oraz}f$ jest ciągła. Jeżeli potencjał $U$ przyjmuje tylko wartości rzeczywiste, to $\lambda\in{\bf R}.$

Mnożąc obie strony (13.12) przez $\overline{f}$ i odejmując stronami od tej równości, równość otrzymaną przez sprzężenie obu stron i pomnożenie ich przez $f$ otrzymamy

$\displaystyle{-\frac{\hbar^{2}}{2m}}\ \Big[\big(\bigtriangleup f\big)\overline{f}-\big(\bigtriangleup\overline{f}\big)f\Big]=\big(\lambda-\overline{\lambda}\big)\ |f\big|^{2}.$

(13.13)

Stosując tożsamość

$\bigtriangleup g\cdot h-\bigtriangleup h\cdot g=div\big(h\cdot gradg-g\ gradh\big),$

w której przyjmiemy $g=f,h=\overline{f}$ i uwzlędniając wzór Gaussa- Ostrogradzkiego

$\displaystyle{\int _{\Omega}divF\ dx=\int _{{\partial\Omega}}F\cdot\stackrel{\rightarrow}{n}\ ds},$

gdzie $F$ jest polem wektorowym na ${\bf R}^{3},$ otrzymamy

$\big(\lambda-\bar{\lambda}\big)\displaystyle{\int _{\Omega}|f|^{2}=-\frac{\hbar^{2}}{2m}\int _{\Omega}div\big(\bar{f}gradf-fgrad\bar{f}dx\big)=\frac{\hbar^{2}}{2m}\int _{{\partial\Omega}}\big(\bar{f}gradf-fgrad\bar{f}\big)\vec{n}\ ds}$

zatem

$\lambda-\bar{\lambda}=\displaystyle{\frac{\hbar^{2}}{2m}\int _{{\partial\omega}}\big(\bar{f}gradf-fgrad\bar{f}\big)\ \vec{n}\ ds\cdot\big(\int _{\Omega}|f|^{2}\ dx\big)^{{-1}}}$

(13.14)

Niech $f(x_{0})\neq 0.$ Mnożąc obie strony równości (13.12) przez odpowiednią liczbę, możemy założyć, że $\bar{f}(x_{0})\cdot gradf(x_{0})\in{\bf R}.$

Wtedy $\bar{f}(x_{0})\cdot gradf(x_{0})-f(x_{0})\cdot grad\bar{f}(x_{0})=0.$ Podstawmy po prawej stronie (13.14) za $\Omega$ kulę $K_{n}$ o środku w $x_{0}$ i promieniu $\frac{1}{n}.$ Wtedy wartość prawej strony dąży do 0, kiedy $n\longrightarrow\infty.$ Wynika stąd, że $\lambda-\bar{\lambda}=0$

∎

W dalszym ciągu tego wykładu zajmiemy się opisem widma operatora energii w przypadku kiedy $U$ jest potencjałem coulombowskim , tj.

$U(x)=\displaystyle{-\frac{e^{2}}{4\pi\epsilon _{0}}\cdot\frac{1}{r}}$

(13.15)

(porównaj (12.7) oraz Stwierdzenie 5.1).

Symetria kulista funkcji $U$ sugeruje, że ten problem jest związany z grupą $S0(3{\bf R}).$ Grupa ta składa się z macierzy ortogonalnych wymiaru 3, tj. macierzy $A=\big(a_{{ij}}\big)_{{i,j=1}}^{3}$ gdzie $a_{{ij}}\in{\bf R}$ takich, że $A^{1}=A^{t}.$ Ustalmy $\lambda\in{\bf R}.$ W dalszym ciągu wygodnie będzie rozpatrywać operator $H_{\lambda}$ o postaci

$H_{\lambda}(f)=\displaystyle{-\frac{\hbar^{2}}{2m}\ \bigtriangleup+U-\lambda I}$

(13.16)

Wtedy $H(f)=\lambda f$ oznacza, że $H_{\lambda}(f)=0.$

Dla grupy $SO(3{\bf R})$ określmy jej naturalną reprezentację (tj homomorfizm) w grupę operatorów ograniczonych i odwracalnych w $L^{2}({\bf R}^{3},dx)$ przyporządkowując elementowi $A\in SO\ (3,{\bf R})$ operator $\widetilde{A}:L^{2}({\bf R}^{3},dx)\rightarrow L^{2}({\bf R}^{3},dx)$ wzorem

$\widetilde{A}f(x)=f\ (Ax)$

(13.17)

Ponieważ dla dowolnego zbioru mierzalnego $\Omega$ oraz $A\in SO(3,{\bf R})$ zachodzi $\mu(\Omega)=\mu(A\Omega),$ gdzie $\mu$ jest miarą Lebesque'a w ${\bf R}^{3}$ to dla $f\in L^{2}({\bf R}^{3},dx)$ oraz $A\in SO(3,{\bf R})$ mamy $\Arrowvert\widetilde{A}f\Arrowvert=\Arrowvert f\Arrowvert.$

Stwierdzenie 13.4

Niech $A\in SO(3{\bf R})$ wtedy

$\bigtriangleup\circ\widetilde{A}=\widetilde{A}\circ\bigtriangleup$

(13.18)

Krok pierwszy.

Niech A będzie macierzą o trzech wierszach i trzech kolumnach i niech
$A\in{\bf R}^{3}.$ Oznaczmy

$\displaystyle{\frac{\partial}{\partial a}f(p)=lim_{{t\to\infty}}\frac{f(p+ta)-f(p)}{t}}$

a przez $\displaystyle{\frac{\partial}{\partial a}}$ oznaczymy operację liniową tej pochodnej przy zmiennym $f.$

Niech $\widetilde{A}f(x)=f(Ax).$ Wtedy

$\displaystyle{\frac{\partial}{\partial a}\circ\widetilde{A}=\widetilde{A}\circ\frac{\partial}{\partial(Aa)}}.$

(13.19)

Dowód polega na łatwych rachunkach i pozostawimy go czytelnikowi.

Oznaczmy $\displaystyle{\frac{\partial^{2}}{\partial b\ \partial a}=\frac{\partial}{\partial b}\circ\frac{\partial}{\partial a}}$ wtedy z (13.3.8) otrzymamy

$\displaystyle{\frac{\partial^{2}}{\partial b\ \partial a}\circ\widetilde{A}=\widetilde{A}\circ\frac{\partial^{2}}{\partial(Ab)\ \partial(Aa)}}.$

(13.20)

Krok drugi.

Niech $A=\big(a_{{ij}}\big)_{{i,j=1}}^{3}\in SO(3,{\bf R}).$ Oznaczając przez $e_{i}\\ i=1,2,3$ wersory osi mamy

$\bigtriangleup=\displaystyle{\frac{\partial^{2}}{(\partial e_{1})^{2}}+\frac{\partial^{2}}{(\partial e_{2})^{2}}+\frac{\partial^{2}}{(\partial e_{3})^{2}}}$

zatem z (13.20)

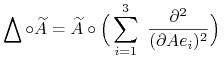$\bigtriangleup\circ\widetilde{A}=\widetilde{A}\circ\Big(\displaystyle\sum _{{i=1}}^{3}\ \frac{\partial^{2}}{(\partial Ae_{i})^{2}}\Big)$

ale

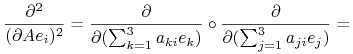$\displaystyle{\frac{\partial^{2}}{(\partial Ae_{i})^{2}}=\frac{\partial}{\partial(\sum _{{k=1}}^{3}a_{{ki}}e_{k})}\circ\frac{\partial}{\partial(\sum _{{j=1}}^{3}a_{{ji}}e_{j})}}=$

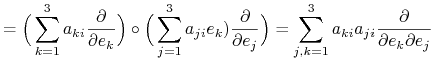$\displaystyle{=\Big(\sum _{{k=1}}^{3}a_{{ki}}\frac{\partial}{\partial e_{k}}\Big)\circ\Big(\sum _{{j=1}}^{3}a_{{ji}}e_{k})\frac{\partial}{\partial e_{j}}\Big)=\sum _{{j,k=1}}^{3}a_{{ki}}a_{{ji}}\frac{\partial}{\partial e_{k}\partial e_{j}}}$

zatem

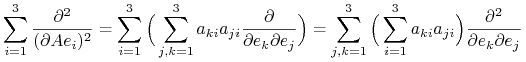$\displaystyle{\sum _{{i=1}}^{3}\frac{\partial^{2}}{(\partial Ae_{i})^{2}}=\sum _{{i=1}}^{3}\Big(\sum _{{j,k=1}}^{3}a_{{ki}}a_{{ji}}\frac{\partial}{\partial e_{k}\partial e_{j}}\Big)=\sum _{{j,k=1}}^{3}\Big(\sum _{{i=1}}^{3}a_{{ki}}a_{{ji}}\Big)\frac{\partial^{2}}{\partial e_{k}\partial e_{j}}}$

i z warunku $A^{t}=A^{{-1}}$ wynika, że współczynnik przy $\displaystyle{\frac{\partial}{\partial e_{k}\partial e_{j}}}$ wynosi 1 jeżeli $j=k$ oraz 0 jeżeli $j\neq k,$ co należało wykazać.

∎

Oznaczmy

$kerH_{\lambda}=\{ f\in L^{2}({\bf R}^{3},dx):H_{\lambda}=0\}$

(13.21)

Wniosek 13.1

$kerH_{\lambda}$ jest domkniętą podprzestrzenią liniową $L^{2}({\bf R}^{3},dx),$ która jest niezmiennicza dla naturalnej reprezentacji $SO(3,\bf R),$ tj dla $A\in SO(3,\bf R)$ oraz $f\in kerH_{\lambda}$ także $\widetilde{A}f\in kerH_{\lambda}.$

Część pierwsza jest konsekwencją domkniętości operatora $H_{\lambda},$ której nie będziemy uzasadniać. Jeżeli $f\in kerH_{\lambda},$ tj $H_{\lambda}f=0$ to