« 13. Równanie Schrödingera  Spis treści  Literatura »

Zagadnienia

14. Widmo operatora energii dla atomu wodoru

14.1. Operator Laplace'a i współrzędne sferyczne.

Jak pokazaliśmy w Stwierdzeniu (13.4), operator Laplace'a jest przemienny z operatorami naturalnej reprezentacji grupy SO(3{\bf R}). Sytuacja ta sugeruje spojrzenie na {\bf R}^{3}\backslash\{ 0\} jako na produkt sfery S^{2} i prostej R.

Technicznie odbywa się ono poprzez wprowadzenie na sferze współrzędnych ”geograficznych”: współrzędnej \theta - ”szerokości geograficznej” , stałej na ”równoleżnikach” i podającej liczony od 0 do \pi kąt między wektorem położenia a ”osią obrotu Ziemi” ( osią \stackrel{\rightarrow}{0x_{3}} przyjętego układu kartezjańskiego) oraz współrzędnej \varphi - ”długości geograficznej” - stałej na południkach - podającej kąt liczony od 0 do 2\pi od ”południka 0”, za który przyjmiemy linię przecięcia sfery z półpłaszczyzną x_{1}x_{2} dla x_{1}>0. Zatem mamy

x_{1}=r\sin\theta\cos\varphi
x_{2}=r\sin\theta\sin\varphi (14.1)
x_{3}=r\cos\theta

gdzie 0<\theta<\pi,0<\varphi>2\pi oraz 0,r<+\infty jest odległością od zera. Współrzędne (\theta,\varphi)dają po wyrzuceniu południka 0 wraz z biegunami wzajemnie jednoznaczne odwzorowanie płaskiej mapy na sferę.

Wzory (14.1) można traktować albo jako równoległy do kartezjańskiego opis punktów W={\bf R}^{3}\backslash\{\textrm{półpłaszczyzna}x_{1}x_{2}\textrm{dla }x>0\} albo jako wzajemnie jednoznaczne odwzorowanie S:\Omega\rightarrow W, gdzie

\Omega=\big\{(\theta,\varphi,r):0<\theta<\pi,\ \ 0<\varphi<2\pi,0<r\big\}\textrm{\ }\ \textrm{na}\ \ W

Tej zamianie współrzędnych odpowiada nowy opis operatora Laplace'a. Przenosząc funkcję F(x,y,z) określoną na W do zbioru \Omega, tak że jej obraz wynosi

\widetilde{F}(\theta,\varphi,r)=(F\circ S)(\theta,\varphi,r).

Po żmudnych rachunkach otrzymujemy

\bigtriangleup(\widetilde{F})=\frac{1}{r^{2}}\Big[\frac{\partial}{\partial r}\Big(r^{2}\ \frac{\partial}{\partial r}\Big)+\frac{1}{\sin\theta}\frac{\partial}{\partial\theta}\big(\sin\theta\frac{\partial}{\partial\theta}\ \big)+\frac{1}{\sin^{2}\theta}\ \frac{\partial^{2}}{\partial\varphi^{2}}\Big]\widetilde{F}(\theta,\varphi,r) (14.2)

Przedmiotem naszego zainteresowania w tym wykładzie będzie widmo punktowe \sigma _{p}H operatora energii (13.8) to znaczy zbiór wartości własnych H. Wiemy już (Stwierdzenie 13.3), że dla potencjału U, przyjmującego wartości rzeczywiste widmo \sigma _{p}(H) przyjmuje wartości rzeczywiste.

W dalszym ciągu dla ustalonej liczby \lambda\in{\bf C} wygodnie będzie rozważać operator H_{\lambda}=H-\lambda I. Oznaczając

kerH_{\lambda}=\{ f\in{\bf L}^{2}({\bf R}^{3},dx):H_{\lambda}f=0\}

Możemy wtedy widmo punktowe H opisać warunkiem:

\sigma _{p}(H)=\{\lambda\in{\bf R}\ \ :\ \ kerH_{\lambda}\neq\{ 0\}\} (14.3)

Oczywiście widmo H zależy od potencjału U.

W tym rozdziale skupimy się na potencjale coulombowskim

U(r)=-\frac{e^{2}}{4\pi\in _{0}}\ \ \frac{1}{r} (14.4)

Strategia naszego postępowania jest następująca:

Korzystając z tego, że potencjał (14.4) jest niezmienniczy dla naturalnego działania grupy SO(3,\bf R) użyjemy niebanalnego faktu (którego dowód naszkicowany jest w punkcie 14.4 ), że w przypadku potencjału sferycznie symetrycznego zachodzi implikacja:

\big(kerH_{\lambda}\neq\{ 0\}\big)\Rightarrow\big(kerH_{\lambda}\ \ \textrm{ zawiera funkcję}\ \ F\ \ \textrm{o postaci (14.5)}\big)
F(\theta,\varphi,r)=\bigtriangleup(\theta)\cdot\Phi(\varphi)\cdot R(r). (14.5)

Następnie, korzystając z postaci (14.2) operatora Laplace'a zastosujemy ”metodę separacji zmiennych ”, prowadzącą do trzech równań różniczkowych zwyczajnych na funkcje \bigtriangleup,\Phi i R z osobna.

Równania te nie są niezależne - łączy je występowanie wspólnych ”stałych separacji”. Ich wyznaczenie za pomocą równań na \varphi i na \theta stanowi drugą część postępowania. Nie korzysta ona z postaci (14.4) naszego potencjału a jedynie z jego symetrii sferycznej.

Krok ostatni, to dyskusja równania na R(r) z wykorzystaniem (14.4). Przynosi ona opis możliwych wartości własnych H zgodny z warunkami Bohra i Balmera. A zatem potwierdza trafność równania Schr\ddot{o}dingera.

14.2. Metoda separacji zmiennych.

W przypadku sferycznie symetrycznego potencjału V, korzystając z opisu (14.2) operatora Laplace'a, otrzymany dla operatora H_{\lambda}=H-\lambda I
warunek H_{\lambda}F=0 w postaci

\Big[\Big(-\frac{\partial}{\partial r}\Big(r^{2}\ \frac{\partial}{\partial r}\Big)+\frac{2mr^{2}}{\hbar^{2}}V(r)-\frac{2mr^{2}}{\hbar^{2}}\lambda\Big)+\Big(\frac{1}{\sin\theta}\frac{\partial}{\partial\theta}\big(\sin\theta\frac{\partial}{\partial\theta}\ \big)+\frac{1}{\sin^{2}\theta}\ \frac{\partial^{2}}{\partial\varphi^{2}}\Big)\Big](F)=0, (14.6)

Jak widzimy, nasz operator zapisuje się w formie

H_{\lambda}=\big(H_{\lambda}\big)_{r}+\big(H_{\lambda}\big)_{{\theta\varphi}}

gdzie część \big(H_{\lambda}\big)_{r} zawiera tylko różniczkowanie względem r i mnożenie przez funkcje zależne od r. Analogicznie wygląda sytuacja dla \big(H_{\lambda}\big)_{{\theta\varphi}}, tym razem względem \varphi i \theta oraz funkcji tych argumentów.

Zastosujmy ten operator do funkcji (14.5). Wtedy \big(H_{\lambda}\big)_{r} działa tylko na R(r) a \big(H_{\lambda}\big)_{{\theta\varphi}} tylko na \bigtriangleup(\theta)\cdot\phi(\varphi). W rezultacie dzieląc całości przez F i przenosząc na prawą stronę część zależną od \theta,\varphi otrzymamy

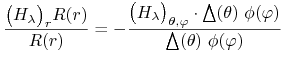\frac{\big(H_{\lambda}\big)_{r}R(r)}{R(r)}=-\frac{\big(H_{\lambda}\big)_{{\theta,\varphi}}\cdot\bigtriangleup(\theta)\ \phi(\varphi)}{\bigtriangleup(\theta)\ \phi(\varphi)} (14.7)

Ponieważ po lewej stronie (14.7) mamy funkcję zmiennej r a po prawej zmiennych \theta i \varphi, równość ta może zachodzić tylko wtedy , kiedy obie strony są stałe. Otrzymamy więc:

(H_{\lambda}\big)_{r}R(r)=cR(r)
(H_{\lambda}\big)_{{\theta,\varphi}}\cdot\bigtriangleup(\theta)\ \phi(\varphi)=-c\bigtriangleup(\theta)\ \phi(\varphi)

Ostatnia równość po podstawieniu postaci (H_{\lambda}\big)_{{\theta,\varphi}} i po pomnożeniu przez \sin^{2}\theta przyjmie formę:

\displaystyle{\Big[\sin\theta\frac{\partial}{\partial\theta}\big(\sin\theta\frac{\partial}{\partial\theta}\big)+\frac{\partial^{2}}{\partial\varphi^{2}}\Big]\bigtriangleup(\theta)\phi(\varphi)}=-c\bigtriangleup(\theta)\phi(\varphi)\cdot\sin^{2}\theta,

Wykonując różniczkowania, dzieląc przez \bigtriangleup(\theta)\phi(\varphi), i przenosząc wyrazy zawierające \theta na jedną stronę a zawierające \varphi na drugą, otrzymamy

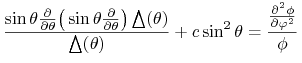\displaystyle{\frac{\sin\theta\frac{\partial}{\partial\theta}\big(\sin\theta\frac{\partial}{\partial\theta}\big)\bigtriangleup(\theta)}{\bigtriangleup(\theta)}+c\sin^{2}\theta=\frac{\frac{\partial^{2}\phi}{\partial\varphi^{2}}}{\phi}}

skąd, podobnie jak poprzednio lewa strona i prawa strona równe są stałej d. Otrzymamy zatem równania

{\frac{d^{2}\phi}{d\varphi^{2}}=d\phi} (14.8)

oraz

{\sin^{2}\theta\ \ \frac{d^{2}\bigtriangleup}{d\theta^{2}}+\sin\theta\ \cos\theta\ \frac{d\bigtriangleup}{d\theta}+\big(c\sin^{2}\theta-d\big)\ \bigtriangleup=0.} (14.9)

Każde rozwiązanie równania (14.8) jest kombinacją liniową funkcji \displaystyle{e^{{i\sqrt{d}\varphi}}} gdzie \sqrt{d} ma dwie wartości zespolone. Na to, aby \phi(\varphi) była funkcją 2\pi okresową - co wynika z opisu we współrzędnych sferycznych, różniczkowalnej na {\bf R}^{3}\backslash\{ 0\} funkcji F(\theta,\varphi,r)=R(r)\bigtriangleup(\theta)\Phi(\varphi), potrzeba i wystarcza by d=m^{2} dla m\in Z. Zatem stała separacji c musi być taka żeby określone na (0,\pi) równanie (14.9) miało rozwiązania określone na (0,\pi.)

14.3. Kroki redukujące.

Zajmiemy się równaniem (14.9). Naszym celem jest pokazanie, że ma ono niezerowe rozwiązanie na (0,\pi) tylko wówczas, gdy c=l(l+1) dla l=0,1,2,...

Postępowanie polega na przechodzeniu do coraz prostszych równań w taki sposób, że kolejne równania zawierają c jako parametr oraz, że posiadanie rozwiązania przy ustalonym c przez równanie poprzednie implikuje posiadanie rozwiązania przy tym samym c przez równanie następne. W rezultacie po pewnej liczbie kroków dochodzimy do równań:

\Big(1-x^{2}\Big)\frac{d^{2}f}{dx^{2}}-2x\frac{df}{dx}-cf=0 (14.10)

Zagadnienie, przy jakim c takie równanie posiada rozwiązania na (-1, 1), jest jednym z klasycznych zadań analizy i wiąże się z teorią wielomianów Legendre'a. w innym sformułowaniu jest to pytanie o widmo punktowe operatora

Af=\Big(1-x^{2}\Big)\frac{d^{2}f}{dx^{2}}-2x\frac{df}{dx}. (14.11)

Nasze postępowanie przebiega w kilku krokach.

Krok pierwszy:

Od równania (14.9) przejdziemy do równania

\big[(1-w^{2})\frac{d^{2}}{dw^{2}}-2w\frac{d}{dw}+(c-\frac{m^{2}}{1-w^{2}})\big]G(w)=0 (14.12)

gdzie G ma być funkcją określoną na (-1,1).

Przejścia dokonujemy, podstawiając \theta=\arccos w, tak, że G(w)=\bigtriangleup(\arccos w) lub inaczej:

\bigtriangleup(\theta)=G(\cos\theta) (14.13)

Z (14.13) otrzymujemy

\displaystyle{\frac{d\bigtriangleup}{d\theta}=-\sin\theta\cdot\frac{dG}{dw}}

oraz

\displaystyle{\frac{d^{2}\bigtriangleup}{d\theta^{2}}=\sin^{2}\theta\frac{d^{2}G}{dw^{2}}-\cos\theta\frac{dG}{dw}}

Wstawiając te wartości do (14.9), po przekształceniach, otrzymamy (14.13).

Krok drugi:

Od równania (14.13) przejdziemy do równania (14.14 ), rozważanego, podobnie jak (14.13), na odcinku (-1, 1).

\Big[\displaystyle{\big(1-w^{2}\big)\frac{d^{2}}{dw^{2}}-2w\big(m+1\big)\frac{d}{dw}+(c-m(m+1)}\big)\Big]U_{m}(w)=0(m) (14.14)

Indeks m pojawia się w (14.14) w związku z następującą dalej redukcją, obniżającą m do m-1 i w konsekwencji doprowadzającą do (14.10) przy (m=0).

Aby przejść od (14.13) do (14.14)(m), przyjmijmy

U_{m}(w)=\displaystyle{\frac{G(w)}{(1-w^{2})^{\frac{m}{2}}}}

a zatem

G(w)=U_{m}(w)(1-w^{2})^{\frac{m}{2}}. (14.15)

Po prostych,lecz pracochłonnych obliczeniach, pokazujemy, że spełnienie przez G o postaci (14.15) warunku (14.12) implikuje, że U_{m} spełnia równanie (14.14)(m).

Krok trzeci:

Lemat 14.1

(a) Jeżeli U_{{m-1}} jest rozwiązaniem (14.14)(m-1) to \displaystyle{\frac{dU_{{m-1}}}{dx}} jest rozwiązaniem równania (14.14)(m). (b) Każde rozwiązanie (14.14)(m) powstaje jako pochodna pewnego rozwiązania równania(14.14)(m-1).

Niech h będzie jakąś funkcją różniczkowalną na (-1,1) i obliczmy wartość wyrażenia

\frac{d}{dw}\Big[\big(1-w^{2})\frac{d^{2}h}{dw^{2}}-wm\frac{dh}{dw}+\big(c-(m-1)m\big)h\Big] (14.16)

Oznaczmy \frac{dh}{dw}=F(w). Wtedy wyrażenie (14.17) przyjmie postać:

-2w\frac{dF}{dw}+(1-w^{2})\frac{d^{2}F}{dw^{2}}-2mF-2wm\frac{dF}{dw}+\big(c-(m-1)m\big)F=
\big(1-w^{2}\big)\frac{d^{2}F}{dw^{2}}-2w(m+1)\frac{dF}{dw}+\big(c-m(m+1)\big)F.

Zatem, dla dowodu (a) należy jako h w (14.16) podstawić U_{{m-1}}. Wtedy wyrażenie w nawiasie kwadratowym jest równe identycznościowo zeru a wobec tego F spełnia równanie (14.14) (m).

Dla dowodu (b) niech F będzie rozwiązaniem (14.14) (m). Wtedy F jest funkcją różniczkowalną, a więc ma funkcję pierwotną h. Przeprowadzając przytoczone rachunki w odwrotnym kierunku i podstawiając F=\displaystyle{\frac{dh}{dw}} otrzymamy równość mówiącą, że wyrażenie (14.17) jest równe zeru. Oznacza to, że h spełnia równanie (14.14)(m-1), w kórym zero po prawej stronie zostało zastąpione przez jakąś stałą. Wtedy modyfikacja h przez dodanie do niego odpowiedniej stałej sprawi, że tak zmienione h spełni (14.14)(m-1).

∎
Wniosek 14.1

Jeżeli równanie (14.9) z parametrem c ma rozwiązanie na (0,\pi), to równanie (14.10) z parametrem c ma rozwiązanie na (-1, 1).

14.4. Wielomiany Legendre'a.

Pojawiają się one w związku z kilku zagadnieniami analizy. Powodem naszego zainteresowania jest ich związek z równaniem Laplace'a. Nie mając zamiaru przedstawić w pełny sposób tej klasy funkcji specjalnych, skoncentrujmy się na jej własnościach związanych z pytaniem:

Problem 14.1

Dla jakich wartości parametru zespolonego c równanie (14.10) posiada niezerowe rozwiązanie?

Definicja 14.1

Wielomian

P_{n}(x)=\frac{1}{2^{n}n!}\ \ \frac{d^{n}}{dx^{n}}\big(x^{2}-1\big)^{n} (14.17)

nazwiemy n-tym wielomianem Legendre'a . Przyjmiemy dodatkowo P_{0}=1. (Mnożenie przez czynnik \ \ \displaystyle{\frac{1}{2^{n}n!}}\ \ daje własność P_{n}(1)=1 i jest naturalne przy innej definicji wielomianów Legendre'a).

Stwierdzenie 14.1

(a) Stopień P_{n} wynosi n. (b) Wielomian P_{n} spełnia równanie (14.10) ze stałą c równą (n-1)n. (Stałą zero w przypadku P_{0}). Znaczy to, że dla operatora

A=\frac{d}{dx}\Big[\big(1-x^{2}\big)\frac{d}{dx}\Big] (14.18)

zachodzi

AP_{n}=(n-1)nP_{n}

(c) Jeżeli c_{1},c_{2} są wartościami własnymi operatora (14.11) oraz c_{1}\neq c_{2} a f_{1} i f_{2} są odpowiadającymi im funkcjami własnymi,to

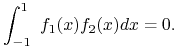\int _{{-1}}^{1}\ f_{1}(x)f_{2}(x)dx=0.

(d) Funkcje P_{0},P_{1},P_{2},... stanowią ortogonalny układ zupełny w przestrzeni L_{2}\big([-1,1],dx\big)

(a) P_{n} otrzymujemy, różniczkując n-krotnie wielomian (x^{2}-1)^{n}stopnia 2n.

(b) Niech W_{n} oznacza przestrzeń wszystkich wielomianów o współczynnikach zespolonych, których stopień nie przekracza n. Ponieważ dla operatora liniowego A danego wzorem (14.11) A(x^{n}) jest też wielomianem stopnia n o współczynniku przy x^{n} równym n(n-1), widzimy, że A(W_{n})=W_{n} dla n=0,1,2...

Pisząc z kolei A w formie

A=\frac{d}{dx}\big[(1-x^{2})\frac{d}{dx}\big] (14.19)

i wykonując dwukrotnie całkowanie przez części, pokazujemy, że

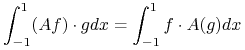\int _{{-1}}^{1}(Af)\cdot gdx=\int _{{-1}}^{1}f\cdot A(g)dx (14.20)

dla dowolnych f i g.

Pokażemy, że w przestrzeni W_{n} istnieje baza ortogonalna f_{0},f_{1},...f_{n} taka, że stopień wielomianu f_{n} wynosi n, oraz Af_{n}=n(n-1)f_{n}.

Postępując indukcyjnie przyjmiemy f_{0}=1, wtedy Af_{0}=0.

Niech będą określone f_{0},...,f_{{n-1}}, stanowiące bazę ortogonalną W_{{n-1}} i będące wektorami własnymi A.

Niech f_{n}\in W_{n} będzie (jedynym z dokładnością do proporcjonalności) wektorem ortogonalnym do W_{{n-1}}. Wtedy na mocy (14.20) Af_{n} jest też ortogonalny do W_{{n-1}} a więc Af_{n}=\lambda f_{n}. Z tego, że Ax^{n} jest stopnia n oraz ma współczynnik przy x^{n} równy n(n-1) wynika, że \lambda=n(n-1).

Pokażemy, że f_{n}=P_{n} (po odpowiednim unormowaniu). W tym celu wystarczy pokazać, że

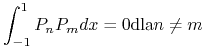\int _{{-1}}^{1}P_{n}P_{m}dx=0\textrm{dla}n\neq m (14.21)

Istotnie, P_{0}=1=f_{0} oraz P_{0},P_{1},P_{{n-1}} rozpinają W_{{n-1}} podobnie jak
f_{0},f_{1},...,f_{{n-1}}, a z pokazanego poprzednio f_{0},...,f_{k} stanowią bazę ortogonalną W_{k} dla k=1,2,...,n.

Pokażemy, że zachodzi (14.21).

Posłużymy się lematem:

Lemat 14.2

Niech k<n, wtedy \frac{d^{k}}{dx^{k}}(x^{2}-1)^{n}=0 dla x\pm 1.

Istotnie

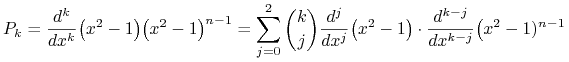P_{k}=\frac{d^{k}}{dx^{k}}\big(x^{2}-1\big)\big(x^{2}-1\big)^{{n-1}}=\sum _{{j=0}}^{2}\binom{k}{j}\frac{d^{j}}{dx^{j}}\big(x^{2}-1\big)\cdot\frac{d^{{k-j}}}{dx^{{k-j}}}\big(x^{2}-1)^{{n-1}}

Pierwszy składnik sumy po stronie prawej zawiera czynnik (x^{2}-1), do pozostałych dwóch składników można stosować założenie indukcyjne. Wykorzystując lemat uzyskujemy (indukcyjnie) (14.21), całkując przez części.

∎

(c) Z warunków \frac{d}{dx}\Big[\big(1-x^{2}\big)\frac{df_{i}}{dx}\Big]=c_{i}f_{i} dla i=1,2 otrzymamy

\displaystyle{\int _{{-1}}^{1}\frac{d}{dx}\Big[\big(1-x^{2}\big)\Big(\frac{df_{1}}{dx}f_{2}-\frac{df_{2}}{dx}f_{1}\Big)\Big]dx=\big(c_{1}-c_{2}\big)\int _{{-1}}^{1}\ f_{1}f_{2}dx}

Lewa strona jest równa \displaystyle{\big(1-x^{2}\big)\Big(\frac{df_{1}}{dx}f_{2}-\frac{df_{2}}{dx}f_{1}\Big)} w granicach 1,-1 a zatem wynosi 0.

(d) Z (b) i (c) wynika ortogonalność funkcji P_{i} a z (a) wynika, że przestrzeń liniowa rozpinana przez P_{0},...P_{n}, jest zarazem przestrzenią rozpinaną przez 1,x,x^{2},...,x^{n}.

Wniosek 14.2

Jedynymi liczbami zespolonymi c, dla których równanie (14.10) ma rozwiązanie są 0,1\cdot 2,2\cdot 3,...m(m+1),...

Funkcja P spełniająca równanie (14.10) jest różniczkowalna na {\bf R}, więc należy do L^{2}\big(\big[-1,1\big],dx\big). Na podstawie punktu (c) Stwierdzenia 14.1 dla c różnego od m(m+1) przy m=0,1,2...) f jako funkcja własna operatora (14.12) byłaby ortogonalna do przestrzeni wszystkich wielomianów, co nie jest możliwe.

∎

14.5. Wartości własne operatora energii dla potencjału coulombowskiego.

Badając wartości własne operatora energii

H=-\frac{\hbar^{2}}{2m}\bigtriangleup+U (14.22)

rozważamy rodzinę operatorów H_{\lambda}=H\lambda-I dla \lambda\in\mathcal{{\bf C}} i badamy warunek H_{\lambda}=0.

W przypadku potencjału coulombowskiego

U(r)=-\frac{e^{2}}{4\pi\in _{0}}\ \ \frac{1}{r}, (14.23)

gdzie e jest ładunkiem elektronu a \in _{0} stałą dielektryczną próżni, wygodnie jest w opisie H_{\lambda} przejść do współrzędnych sferycznych, zapisując warunek H_{\lambda}=0 w postaci (14.6).

Jak pokazaliśmy, metoda separacji zmiennych prowadzi do równania (H_{\lambda})_{r}-cR(r)=0, które po wykonaniu różniczkowań, podzieleniu przez r^{2}, podstawieniu za U potencjału coulombowskiego (14.23) oraz uwzględnieniu, że stała separacji c musi przyjmować jedną z wartości l(l-1) dla l=1,2,3,... przybiera postać:

\Big[\frac{d^{2}}{dr^{2}}+\frac{2}{r}\ \ \frac{d}{dr}+\frac{2l}{\hbar^{2}}\big(\lambda+\frac{e^{2}}{4\pi{\ \in _{0}}r}\big)+\frac{l(l-1)}{r^{2}}\Big]R(r)=0 (14.24)

Naszym celem będzie zbadanie, dla jakich \lambda powyższe równanie posiada rozwiązanie oraz powiązanie otrzymanego warunku z występującymi tu parametrami fizycznymi. (Przypomnijmy, że ze Stwierdzenia(13.3) wynika, że \lambda\in{\bf R} ). W celu możliwie jaknajwiększego uniezależnienia współczynników naszego równania od parametrów fizycznych, przejdziemy do ”unormowanej” zmiennej \displaystyle{\rho=\frac{r}{a_{1}}}, gdzie \displaystyle{a_{1}=\frac{4\pi\in _{0}\hbar^{2}}{me^{2}}} jest promieniem Bohra (porównaj (12.8)). Oznaczymy też \displaystyle{\mu=-\frac{8\pi\in _{0}a_{1}}{e_{2}}\cdot\lambda}.

W wyniku tych zmian otrzymamy równanie

\Big[\frac{d^{2}}{d\rho^{2}}+\frac{2}{\rho}\frac{d}{d\rho}-\frac{l(l-1)}{\rho^{2}}+\frac{2}{\rho}-\mu\Big]R(\rho)=0, (14.25)

gdzie ”obecna” funkcja R jest równa dawnej funkcji R od zmiennej a_{1}\cdot\rho.

Warunek F\in L^{2}({\bf R}^{3},dx) dla F(r,\theta,\varphi)=R(r)\cdot\bigtriangleup(\theta)\cdot\phi(\varphi) prowadzi do warunku:

\int _{0}^{{+\infty}}\big|R(\rho)\big|^{2}\rho^{2}d\rho<+\infty (14.26)

i będziemy szukać rozwiązań (14.24) spełniających (14.25). Przekształcimy równanie (LABEL:14.5.4), aby zależność od parametru l było łatwiej poddać kontroli a także, aby uprościć jego postać.

Wskazówką przy szukaniu odpowiedniego podstawienia mogą być następujące dwie obserwacje: Uproszczenie równania (14.24) do

\Big[\frac{d^{2}}{d\rho^{2}}+\frac{2}{\rho}\frac{d}{d\rho}-\frac{l(l-1)}{\rho^{2}}\Big]\alpha(\rho)=0 (14.27)

daje równanie o podobnych (mamy nadzieję) rozwiązaniach dla małych wartości \rho. Co więcej, dla (14.27) możemy odgadnąć dwa liniowo niezależne rozwiązania. Są nimi

\alpha _{1}(\rho)=\rho^{{l-1}}\textrm{ oraz}\ \ \ \alpha _{2}(\rho)=\rho^{{-l}}.

Z nich tylko \alpha _{1} spełnia dla małych \rho warunek (LABEL:14.5.4). Podobnie dla dużych \rho możemy (14.24) uprościć do

\Big[\frac{d^{2}}{d\rho^{2}}-\mu\Big]\beta(\rho)=0. (14.28)

Równanie to ma dwa liniowo niezależne rozwiązania \displaystyle{\beta _{1}(\rho)=e^{{-\sqrt{\mu}\rho}}} i \displaystyle{\beta _{2}=e^{{\sqrt{\mu}\rho}}}. Ponieważ, jak pokazaliśmy w Stwierdzeniu 13.3, \lambda a zatem \mu są rzeczywiste, to całkowalność rozwiązań (14.28) mamy szansę uzyskać tylko dla \mu>0 ( zatem \lambda<0 ).

W wyniku tych obserwacji zapropononujemy podstawienie

R(\rho)=\rho^{l}e^{{-\sqrt{\mu}\rho}}L(\rho). (14.29)

Wtedy

\displaystyle{\frac{dR}{d\rho}=l\rho^{{l-1}}e^{{-\sqrt{\mu}\rho}}L(\rho){-\sqrt{\mu}\rho}^{l}\ \ e^{{-\sqrt{\mu}\rho}}L(\rho)+\rho^{l}e^{{-\sqrt{\mu}\rho}}\frac{dL}{d\rho}}

oraz

\displaystyle{\frac{d^{2}R}{d\rho^{2}}=l(l-1)\rho^{{l-2}}e^{{-\sqrt{\mu}\rho}}L(\rho)-2l\sqrt{\mu})\rho^{{l-1}}L(\rho)\ \ +\mu\rho^{l}e^{{-\sqrt{\mu}\rho}}L(\rho)+2l\rho^{{l-1}}e^{{-\sqrt{\mu}\rho}}\frac{dL}{d\rho}}-
-\displaystyle{2\sqrt{\mu}\rho^{l}e^{{-\sqrt{\mu}\rho}}\frac{dL}{d\rho}+\rho^{l}e^{{-\sqrt{\mu}\rho}}\frac{d^{2}L}{d\rho^{2}}}

I w rezultacie podstawiając te wartości oraz (14.29 ) do równania (14.27), widzimy, że L musi spełniać równanie:

\Big[\rho\frac{d^{2}}{d\rho^{2}}+2\big(l+1-\rho\sqrt{\mu}\big)\frac{d}{d\rho}+2\big(\frac{l}{\rho}-(l+1)\sqrt{\mu}+1\big)\Big]L(\rho)=0 (14.30)

Rozwińmy funkcję L w szereg Laurenta o środku w 0, to jest niech:

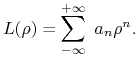\displaystyle{L(\rho)=\sum _{{-\infty}}^{{+\infty}}\ a_{n}\rho^{n}}. (14.31)

Wtedy

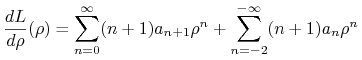\frac{dL}{d\rho}(\rho)=\sum _{{n=0}}^{{\infty}}(n+1)a_{{n+1}}\rho^{n}+\sum _{{n=-2}}^{{-\infty}}(n+1)a_{n}\rho^{n} (14.32)

Widzimy (14.30), że n-ty współczynnik funkcji otrzymanej jako lewa strona równania (identycznościowo równej zero na mocy tegoż równania wynosi:

b_{n}=n(n+1)a_{{n+1}}+2(l+1)(n+1)a_{{n+1}}-2\sqrt{\mu}na_{n}+\big(-2\sqrt{\mu}(l+1)+2\big)a_{n}+2la_{{n+1}}

Ponieważ funkcja równa identycznościowo zeru ma wszystkie współczynniki równe zeru, otrzymamy stąd

a_{{n+1}}\Big[\big(n+1\big)\big(n+2(l+1)\big)+2l\Big]=a_{n}\Big[2\sqrt{\mu}n+2\sqrt{\mu}(l+1)\Big]

skąd

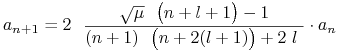a_{{n+1}}=2\ \ \frac{\sqrt{\mu}\ \ \big(n+l+1\big)-1}{(n+1)\ \ \big(n+2(l+1)\big)+2\ l\ }\cdot a_{n} (14.33)

Ze wzoru tego wynika, że dla dużych n stosunek \displaystyle{\frac{a_{{n+1}}}{a_{n}}} zachowuje się jak \displaystyle{\frac{2\sqrt{\mu}}{(n+1)}}, skąd można wyprowadzić, że L(\rho) zachowuje się dla dużych \rho jak e^{{2\sqrt{\mu}\rho}} a zatem R(\rho) nie może być funkcją całkowalną. Jedynym wyjątkiem jest sytuacja, kiedy a_{n}=0 począwszy od pewnego n.

To się może stać wtedy, kiedy

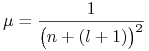\mu=\displaystyle{\frac{1}{\big(n+(l+1)\big)^{2}}}

Przypomnijmy, że przyjęliśmy \displaystyle{\mu=-\frac{8\pi\in _{0}a_{1}}{e^{2}}\ \lambda}, gdzie a_{1}=\displaystyle{\frac{4\pi\ \in _{0}\hbar^{2}}{me^{2}}} jest promieniem Bohra (12.8). Wtedy \mu=\displaystyle{-\frac{\lambda}{R}} gdzie R=\displaystyle{\frac{me^{4}}{32\Pi^{2}\in _{0}^{2}\hbar^{2}}} jest stałą Rydyberga. Ostatecznie otrzymujemy warunek

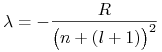\lambda=\displaystyle{-\frac{R}{\big(n+(l+1)\big)^{2}}}

dla l=0,1,2,... oraz n=0,1,2,..., zgodny z (12.9).

14.6. Funkcje własne operatora energii dla potencjału o symetrii sferycznej.

W punkcie tym pokażemy, że w przypadku potencjału V, który we współrzędnych (14.1) zależy jedynie od r, przestrzeń kerH_{\lambda}, o ile nie jest równa \{ 0\} zawiera funkcje o postaci

F(r,\theta,\varphi)=R(r)\cdot\bigtriangleup(\theta)\cdot\phi(\varphi). (14.34)

Redukcja ta nie zależy od postaci operatora H_{\lambda} a jedynie od tego, że jest on przemienny z naturalną reprezentacją grupy SO(3,\bf R), Wynika stąd, że Y=kerH_{\lambda} jest zachowana przez operatory \widetilde{A} dla A\in SO(3\bf R).

Dla krótkości niech G=SO(3,\bf R), niech \rho oznacza naturalną reprezentację G w L^{2}({\bf R}^{3},dx), to znaczy dla G\ni g=A\in SO(3,{\bf R}) niech \rho _{g}(f)=\widetilde{A}f.

Pierwszym krokiem do pokazania (14.34) jest następujący

Lemat 14.3

Jeżeli Y\neq\{ 0\} jest domkniętą przestrzenią niezmienniczą reprezentacji \rho składającą się z funkcji różniczkowalnych, to Y zawiera funkcje o postaci

F(r,\theta,\varphi)=R(r)\cdot\mathcal{H}(\theta,\varphi) (14.35)

Dowód lematu korzysta z teorii reprezentacji unitarnych zwartych grup topologicznych. Potrzebne fragmenty tej teorii podane są w następnym punkcie tego wykładu.

Idea dowodu Lematu

Niech \displaystyle{d\mu _{r}} oznacza unormowaną miarę Lebesque'a na sferze S_{r} ( tj. o środku 0 i promieniu r) w {\bf R}^{3}. Niech \displaystyle{\rho^{r}} oznacza reprezentację G w L^{2}(S_{r},d_{{\mu _{r}}}) indukowaną przez naturalne działania G na S_{r}.

Dla ustalonego r określmy \Pi _{r}:Y\longrightarrow L^{2}(S_{r},d\mu _{r}), kładąc \Pi _{r}f=\gamma gdzie \gamma(\theta,\varphi)=f(r,\theta,\varphi).

Z Twierdzenia 14.1 wynika, że istnieje skończenie wymiarowa \rho-niezmiennicza podprzestrzeń zespolona Z\subset Y, taka, że \rho ograniczona do Z jest nieprzywiedlna.

Jeżeli funkcje f_{i}(r,\theta,\varphi)\ \ i=1,2,...,d stanowią bazę ortonormalną Z, to reprezentację \rho ograniczoną do Z można opisać wzorem

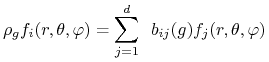\rho _{g}f_{i}(r,\theta,\varphi)=\displaystyle{\sum _{{j=1}}^{d}}\ \ b_{{ij}}(g)f_{j}(r,\theta,\varphi) (14.36)

gdzie B(g)=\big(b_{{ij}}(g)\big)_{{ij=1}}^{d} przebiega pewną (nieprzywiedlnie działającą na \mathcal{C}^{d} ) podgrupą grupy unitarnej U(d).

Ponieważ działanie grupy G dotyczy współrzędnych \theta i \varphi to z \rho-niezmienniczości przestrzeni Z wynika \rho-niezmienniczość przestrzeni Z_{r}=\Pi _{r}(Z). Oznaczmy

h_{i}^{r}=\Pi _{r}f_{i}\ \ i=1,...d\ \textrm{gdzie}\ \ h^{r}_{i}(\theta,\varphi)=f(r,\theta,\varphi)

Wtedy

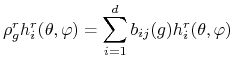\rho _{g}^{r}h_{i}^{r}(\theta,\varphi)=\sum _{{i=1}}^{d}b_{{ij}}(g)h_{i}^{r}(\theta,\varphi) (14.37)

Zauważmy teraz, że dla każdej pary r_{1},r_{2} przekształcenie i_{{r_{1},r_{2}}}(r,\theta,\varphi):S_{{r_{1}}}\longrightarrow S_{{r_{2}}} określone we współrzędnych sferycznych wzorem i_{{r_{1},r_{2}}}(r_{2},\theta,\varphi)=(r_{1},\theta,\varphi) pozwala utożsamić S_{{r_{1}}} z S_{{r_{2}}} i indukuje przekształcenie unitarne

\displaystyle{I_{{r_{1},r_{2}}}:L^{2}(S_{{r_{1}}},d\mu _{{r_{1}}})\rightarrow L^{2}(S_{{r_{2}}},d\mu _{{r_{2}}})}

i przy tym, dla dowolnych r_{1},r_{2} oraz g\in G

I_{{r_{1},r_{2}}}\cdot\rho _{g}^{{r_{1}}}=\rho _{g}^{{r_{2}}}\cdot I_{{r_{1},r_{2}}} (14.38)

Zatem \displaystyle{I_{{r_{1},r_{2}}}} dają utożsamienie przestrzeni L^{2}(S_{r},d\mu _{r}) wraz z działaniem G.

Zauważmy, że przy każdym r funkcje h_{i} są liniowo niezależne. Istotnie, gdyby k spośród nich rozpinało przestrzeń Z_{r} dla pewnego k<d to operatory B(g) dla g\in G działaby z przestrzenią niezmienniczą w \mathcal{C}^{d}.

Z utożsamienia (LABEL:14.6.5) reprezentacji \rho^{r} dla różnych r wynika, że wszystkie one mają ten sam rozkład na ortogonalną sumę prostą reprezentacji nieprzywiedlnych. Z tego, że reprezentacje \rho^{r} są cykliczne wynika, że każda reprezentacja nieprzywiedlna może pojawić się w tym rozkładzie tylko skończoną (\leq od swojego wymiaru) liczbę razy. Dwie reprezentacje nieprzywiedlne pojawiające się w rozkładzie są identyczne lub działają w przestrzeniach ortogonalnych.

Ponieważ małej zmianie r odpowiada mała zmiana bazy ( h_{1}^{r},...h_{d}^{r}) i ponieważ wzór (14.36) określa reprezentację nieprzywiedlną, wynika stąd, h_{i}^{r} nie zależą od r, to jest

h_{i}^{r}(\theta,\varphi)=h_{i}(\theta,\varphi)\ \ \textrm{dla wszystkich}\ \ r

Ale to wtedy znaczy, że

f_{i}(r,\theta,\varphi)=R(r)\cdot h_{i}(\theta,\varphi).

Wynika stąd teza.

Uwaga 14.1

Przytoczone rozumowanie pokazuje też, że \displaystyle{Z_{r}=Z_{1}\cdot\frac{R(r)}{R(1)}}.

Niech S będzie sferą w {\bf R}^{3} i d\mu unormowaną miarą Lebesque'a na S. Ograniczmy reprezentację \rho do 1-parametrowej podgrupy SO(3\bf R) składającej się z obrotów wokół osi x_{3}, to jest w przyjętych współrzędnych sferycznych przekształcenie A_{{\varphi _{0}}}, będące obrotem o kąt \varphi _{0}, ma postać

(\theta,\varphi)\longrightarrow(\theta,\varphi+\varphi _{0})\ \ (mod.2\pi).
Lemat 14.4

Niech Z\neq\{ 0\} będzie domkniętą przestrzenią niezmienniczą dla przekształceń A_{\varphi},0\leq\varphi<2\pi. Istnieje 0\neq h\in Z oraz liczba całkowita n_{0} takie, że

h(\theta,\varphi)=e^{{in_{0}\varphi}}\cdot\bigtriangleup(\theta). (14.39)

Dla liczby całkowitej n rozpatrzmy operator T_{n} dany wzorem

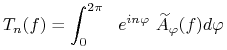T_{n}(f)=\int _{0}^{{2\pi}}\ \ e^{{in\varphi}}\ \widetilde{A}_{\varphi}(f)d\varphi (14.40)

Twierdzimy, że istnieje n_{0} oraz f\in Z, że T_{{n_{0}}}(t)\neq 0. Istotnie, w przeciwnym razie dla każdej funkcji ciągłej \chi mielibyśmy:

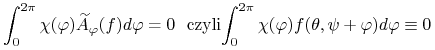\displaystyle{\int _{0}^{{2\pi}}\chi(\varphi)\widetilde{A}_{\varphi}(f)d\varphi}=0\ \ \textrm{czyli}\displaystyle{\int _{0}^{{2\pi}}\chi(\varphi)f(\theta,\psi+\varphi)d\varphi}\equiv 0

Nie tracąc ogólności możemy założyć, że f(\theta _{0},\varphi _{0})\neq 0, że f jest ciągła, \chi jest rzeczywista nieujemna oraz, że nośnik \chi jest zawarty w dowolnie małym otoczeniu ((\theta _{0},\varphi _{0}). Dostajemy stąd sprzeczność. Szczegóły pozostawiamy czytelnikowi.

Niech zatem T_{{n_{0}}}f\neq 0 dla pewnej funkcji f\in Z. Wtedy T_{{n_{0}}}f\in Z i twierdzimy, że T_{{n_{0}}}f(\theta,\varphi)=e^{{-in_{0}\varphi}}\cdot\bigtriangleup(\theta).

Istotnie

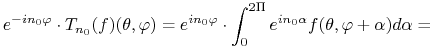\displaystyle{e^{{-in_{0}\varphi}}\cdot T_{{n_{0}}}(f)(\theta,\varphi)=e^{{in_{0}\varphi}}\cdot\displaystyle{\int _{0}^{{2\Pi}}e^{{in_{0}\alpha}}f(\theta,\varphi+\alpha)d\alpha=}}
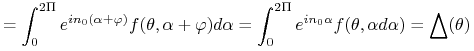=\displaystyle{\int _{0}^{{2\Pi}}e^{{in_{0}(\alpha+\varphi)}}f(\theta,\alpha+\varphi)d\alpha=\int _{0}^{{2\Pi}}e^{{in_{0}\alpha}}f(\theta,\alpha d\alpha)=\bigtriangleup(\theta)}
∎
Wniosek 14.3

W każdej różnej od zera przestrzeni kerH_{\lambda} znajduje się funkcja F postaci

F(r,\theta,\varphi)=R(r)\cdot\bigtriangleup(\theta)\cdot e^{{in_{0}\varphi}} (14.41)

14.7. Wybór faktów z teorii reprezentacji grup zwartych.

Definicja 14.2

Grupą topologiczną nazywamy grupę G, która jest jednocześnie przestrzenią topologiczną, przy czym odwzorowanie

G\times G\ni(a,b)\longrightarrow a_{{-1}}b\in G

jest ciągłe.

Grupę topologiczną nazywamy zwartą (odpowiednio lokalnie zwartą) jeżeli jako przestrzeń topologicznie jest ona zwarta (lokalnie zwarta).

Definicja 14.3

Miarę \mu określoną na \sigma- ciele \sum podzbiorów grupy G nazywamy lewostronnie (odpowiednio prawostronnie) niezmienniczą jeżeli dla każdego A\in\sum oraz g\in G zbiór gA\in\sum ( odpowiednio Ag\in\sum) oraz jeżeli \mu(gA)=\mu(A) (odpowiednio ( \mu(Ag)=\mu(A)).

Uwaga 14.2

Przekształcenie G\ni g\longrightarrow g^{{-1}}\in G indukuje odwzorowanie miar. Obrazem miary lewostronnie niezmienniczej jest miara prawostronnie niezmiennicza (i odwrotnie). Wobec tego każde zdanie o miarach lewostronnie niezmienniczych ma swój odpowiednik dla miar prawostronnie niezmienniczych. W dalszym ciągu w związku z lewicowymi sympatiami autora będziemy formułowac teorię dla miar lewostronnie niezmienniczych.

Twierdzenie 14.1

(Alfred Haar)

Na każdej lokalnie zwartej grupie topologicznej G istnieje określona na \sigma-ciele \sum podzbiorów borelowskich G regularna miara lewo niezmiennicza. (Regularność miary oznacza, że dla każdego \mathcal{E}>0 i A\in\sum istnieje zbiór zwarty Z i otwarty Q, takie, że Z\subset A\subset Q oraz \mu(Q\backslash Z)<\mathcal{E}.)

Miara ta ( zwana lewą miarą Haara) jest jedyna w tym sensie, że każde dwie takie miary są proporcjonalne. Miara Haara \mu grupy zwartej jest skończona ( na ogół normuje się ją tak, żeby \mu(G)=1). Własność skończoności miary Haara charakteryzuje grupy zwarte w klasie grup lokalnie zwartych.

Definicja 14.4

Niech G będzie grupą a GL(X) grupą wszystkich odwracalnych przekształceń liniowych przestrzeni liniowej X ze złożeniem przekształceń jako operacją grupową.

Homomorfizm \rho:G\longrightarrow GL(X) nazwiemy reprezentacją G.

Reprezentację nazwiemy skończenie wymiarową (wymiaru n) jeżeli X ma wymiar n.

Najczęściej rozważa się reprezentacje, gdzie X jest przestrzenią nad {\bf C}. Dla grup topologicznych właściwym jest rozważanie reprezentacji ciągłych. Wtedy X powinna też być przestrzenią topologiczną. Najczęściej używanym posulatem ciągłości reprezentacji jest warunek ciągłości trajektorii (nazywany w dalszym tekście ciągłością reprezentacji): dla każdego ustalonego x\in X funkcje G\ni g\longrightarrow\rho _{g}(x)\in X są ciągłe.

Reprezentacja jest cykliczna, jeżeli istnieje x\in X taki, że przestrzeń liniowa Y_{x} rozpinana przez trajektorię

G\cdot x=\{ y\in X:y=\rho _{g}(x)\ g\in G\}

jest gęsta w X.

Jeżeli warunek gęstości Y_{x} zachodzi dla każdego x\neq 0, to reprezentacja nazywa się nieprzywiedlna.

Reprezentacja \rho nazywa się unitarną, jeżeli X jest przestrzenią Hilberta a operatory \rho _{g} reprezentacji \rho są operatorami unitarnymi to jest (\rho _{g})^{*}=(\rho _{g})^{{-1}}=\rho _{{g^{{-1}}}} dla \ g\in G. O dwóch reprezentacjach \rho _{1} i \rho _{2} grupy G działających odpowiednio w przestrzeniach X_{1} i X_{2} powiemy, że są równoważne, jeżeli istnieje liniowy izomorfizm I:X_{1}\longrightarrow X_{2} (topologiczny, jezeli X_{1} i X_{2} są topologiczne) taki, że I\rho _{1}(g)=\rho _{2}(g)I dla g\in G. Reprezentacje równoważne są w pewnym sensie takie same a różnią się tylko opisem.

Stwierdzenie 14.2

Każda lokalnie zwarta grupa topologiczna posiada injektywną reprezentacją unitarną. Jest nią lewa regularna reprezentacja opisana w następujący sposób:

Przestrzenią X jest L^{2}(G,d\mu), gdzie d\mu oznacza lewą miarę Haara, natomiast (\rho _{g}f)(h)=f(gh).

Twierdzenie 14.2

(Podstawowe twierdzenie o ciągłych reprezentacjach unitarnych grup zwartych).

(a) Każda ciągła reprezentacja nieprzywiedlna grupy zwartej jest skończenie wymiarowa.

(b) Każda ciągła hilbertowska reprezentacja grupy zwartej równoważna jest reprezentacji unitarnej.

(c) Każda ciągła reprezentacja unitarna grupy zwartej w ośrodkowej przestrzeni Hilberta rozkłada się na ortogonalną sumę prostą reprezentacji nieprzywiedlnych

X=\oplus X_{n} (14.42)

gdzie każda z przestrzeni X_{n} w (14.42) jest \rho-niezmiennicza oraz \rho-ograniczona do X_{n} jest nieprzywiedlna. Krotnością występowania danej reprezentacji nieprzywiedlnej w rozkładzie (14.42) nazwiemy liczbę składników, dla których eprezentacja \rho ograniczona do X_{i} jest równoważna tej reprezentacji.

(d) Reprezentacja o rozkładzie (14.42) jest cykliczna wtedy i tylko wtedy, gdy krotność występowania w tym rozkładzie dowolnej reprezentacji nieprzywiedlnej jest niewiększa niż jej wymiar.

« 13. Równanie Schrödingera  Spis treści  Literatura »

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

strona główna | webmaster | o portalu | pomoc

© Wydział Matematyki, Informatyki i Mechaniki UW, 2009-2010. Niniejsze materiały są udostępnione bezpłatnie na licencji Creative Commons Uznanie autorstwa-Użycie niekomercyjne-Bez utworów zależnych 3.0 Polska.

Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego.

Projekt współfinansowany przez Ministerstwo Nauki i Szkolnictwa Wyższego i przez Uniwersytet Warszawski.