Zagadnienia

4.1 Pęd i moment pędu
4.2 Układy izolowane
4.3 Układy potencjalne
4.4 Zagadnienie dwóch ciał.

4. Symetrie i całki pierwsze

4.1. Pęd i moment pędu

Omówimy teraz kilka typowych przykładów symetrii w układach mechanicznych. Przez symetrię rozumiemy tu dodatkowe warunki, jakie spełniają siły występujące w rozważanym układzie mechanicznym.

Pierwszym takim warunkiem zaobserwowanym w poprzednim wykładzie (dla układu jednopunktowego) jest potencjalność występującej siły. Konsekwencją tej symetrii jest pojawienie się całki pierwszej - energii całkowitej rozpatrywanego punktu.

W dalszym tekście wygodnie będzie traktować układ n-punktów w ${\bf R}^{3}$ jako jeden punkt w ${\bf R}^{{3n}}$ . Jak zauważyliśmy w Wykładzie 3 przestrzeń fazową $\mathcal{F}$ takiego układu, którą jest wiązka styczna do ${\bf R}^{{3n}}$ możemy utożsamiać z
${\bf R}^{{3n}}\times{\bf R}^{{3n}}$ t.j. $\mathcal{F}={\bf R}^{{6n}}.$

Punkt przestrzeni $\mathcal{F}$ ma wtedy współrzędne

$(x_{1},...x_{n},v_{1},...v_{n})$

(4.1)

gdzie $x_{i}\in{\bf R}^{3}$ jest położeniem $i-$ tego punktu a $v_{i}\in{\bf R}^{3}$ jest jego prędkością.

Definicja 4.1

(a) Niech ruch punktu materialnego o masie $M$ opisany będzie krzywą gładką ${\bf R}\ni t\rightarrow x(t)\in{\bf R}^{3}$ . Pędem tego punktu w chwili $t$ nazwiemy $m\dot{x}(t)\in{\bf R}^{3}.$

(b) Niech ruch układu $\mathcal{M}$ $n-$ punktów o masach $m_{1},...,m_{n}$ opisany będzie krzywą w przestrzeni fazowej $\mathcal{F}(\mathcal{M})={\bf R}^{{3n}}\times{\bf R}^{{3n}}:$

$\dot{\gamma}:{\bf R}\ni t\rightarrow\big((x_{1}(t),...x_{n}(t),\dot{x}_{1}(t),...\dot{x}_{1}(t)\big)\ni\mathcal{F}(\mathcal{M})$

Pędem tego układu w chwili $t$ nazwiemy wektor

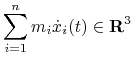$\sum _{{i=1}}^{n}m_{i}\dot{x}_{i}(t)\in{\bf R}^{3}$

(4.2)

$\big[x(t),m\dot{x}(t)\big]\in{\bf R}^{3}$

gdzie $[a,b]$ oznacza iloczyn wektorowy wektorów $a,b\in{\bf R}^{3}.$

(d) Dla układu $\mathcal{M}$ z punktu $(b)$ momentem pędu tego układu w chwili $t$ nazwiemy wektor

$\sum _{{i=1}}^{n}\big[x_{i}(t),m_{i}\dot{x}(t)\big]\in{\bf R}^{3}$

(4.3)

Uwaga 4.1

(a) Zarówno w przypadku pędu jak i momentu pędu mamy do czynienia z następującą sytuacją. Na przestrzeni fazowej $\mathcal{F}(\mathcal{M})$ są określone funkcje

$P:\mathcal{F}(\mathcal{M})\rightarrow{\bf R}^{3}$ zwana pędem oraz

$P:\mathcal{F}(\mathcal{M})\rightarrow{\bf R}^{3}$ zwana momentem pędu
takie, że formuły (4.2) i (4.3) otrzymamy jako superpozycje odpowiednio $P\circ\dot{\gamma}$ i $M\circ\dot{\gamma}.$

(b) Można rozważać także moment pędu względem ustalonego punktu $x_{0}\in{\bf R}^{n},$ dany formułą ${\bf R}\ni t\rightarrow\big[x(t)-x_{0},m\dot{x}(t)\big]$ z podobną zmianą formuły (4.3).

4.2. Układy izolowane

Niech dany będzie układ n-punktów. Siłę $F_{j}$ działającą na $j-$ ty punkt można zapisać w postaci

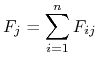$F_{j}=\displaystyle{\sum _{{i=1}}^{n}F_{{ij}}}$

gdzie $F_{{ij}}$ dla $i\neq j$ jest siłą z jaką $i-$ ty punkt oddziaływuje na $j-$ ty, natomiast $F_{{jj}}$ jest siłą działającą na $j-$ ty punkt z zewnątrz. Będziemy przy tym zakładać, że siła $F_{{ij}}$ jest równoległa do wektora $x_{i}-x_{j}$ , gdzie $x_{i}\in{\bf R}^{3}$ jest położeniem $i-$ tego punktu.

Otrzymujemy zatem opis działających sił w formie macierzy

$F=\big(F_{{ij}}\big)_{{i,j=1}}^{n}$

(4.4)

gdzie siłę działającą na punkt $j-$ ty otrzymujemy jako sumę sił występujących w $j-$ tej kolumnie.

Definicja 4.2

Układ n-punktów nazwiemy izolowanym, jeżeli macierz $F$ jest antysymetryczna, tj. jeżeli $F_{{ij}}=-F_{{ji}}.$ Warunek ten zawiera dwa ważne warunki częściowe. Po pierwsze siła zewnętrzna $F_{{jj}}$ działająca na $j-$ ty punkt jest zerowa.

Po drugie suma wszystkich sił działających na punkty tworzące układ jest zerowa, tj

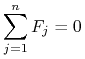$\sum _{{j=1}}^{n}F_{{j}}=0$

(4.5)

Twierdzenie 4.1

Dla układów izolowanych pęd układu $P$ oraz moment pędu układu $M$ są całkami pierwszymi ruchu.

Niech

$\dot{\gamma}(t)=\big(x_{1}(t),...,x_{n}(t),\dot{x}_{1}(t),...,\dot{x}_{n}(t)\big)$

będzie krzywą ruchu w przestrzeni fazowej $\mathcal{F}$ rozważanego układu.

Mamy pokazać, że

$(P\circ\dot{\gamma})(t)=\sum _{{i=1}}^{n}m_{i}\dot{x}_{i}(t)\ \ \ \textrm{oraz}\ \ (M\circ\dot{\gamma})(t)=\sum _{{i=1}}^{n}\big[x_{i}(t),m_{i}\dot{x}_{i}(t)\big],$

gdzie $m_{i}$ jest masą $i-$ tego punktu, są całkami pierwszymi.

Na mocy warunku (4.5) mamy

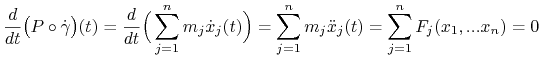$\frac{d}{dt}\big(P\circ\dot{\gamma}\big)(t)=\frac{d}{dt}\Big(\sum _{{j=1}}^{n}m_{j}\dot{x}_{j}(t)\Big)=\sum _{{j=1}}^{n}m_{j}\ddot{x}_{j}(t)=\sum _{{j=1}}^{n}F_{j}(x_{1},...x_{n})=0$

Podobnie wykorzystując (4.5) oraz własność $[w,w]=0$ dla $w\in{\bf R}^{3}$ otrzymamy

$\frac{d}{dt}\big(M\circ\dot{\gamma}\big)(t)=\frac{d}{dt}\Big(\sum _{{j=1}}^{n}\big[x_{j}(t),m_{j}\dot{x}_{j}(t)\big]\Big)=$

$=\sum _{{j=1}}^{n}\Big(\big[\dot{x}_{j}(t),m_{j}\dot{x}_{j}(t)\big]+\big[x_{j}(t),m_{j}\ddot{x}_{j}(t)\big]\Big)=\sum _{{j=1}}^{n}\big[x_{j}(t),F_{j}(x_{1},...x_{n})\big]=$

$=\sum _{{j=1}}^{n}\big[x_{j}(t),\sum _{{i=1}}^{n}F_{{ij}}(x_{1},...x_{n})\big]=\sum _{{ij=1}}^{n}\big[x_{j}(t)F_{{ij}}(x_{1},...x_{n})\big]$

Wykorzystując antysymetrię macierzy sił $F$ możemy ostatnią sumę zapisać jako sumę po wszystkich parach $(i,j)(j,i)$ podwójnych indeksów, gdzie drugi podwójny indeks otrzymujemy przez transpozycję pierwszego. Pokażemy, że wynik sumowania w każdej takiej parze daje zero, t.j., że

$\big[x_{i}(t)F_{{ji}}(x_{1},...x_{n})\big]+\big[x_{j}(t)F_{{ij}}(x_{1},...x_{n})\big]=0$

(4.6)

Istotnie, z własności iloczynu wektorowego wynika, że w obydwu składnikach sumy w (4.6) możemy zastąpić odpowiednio $x_{i}$ przez $x_{i}+\lambda((x_{1}-x_{2})$ oraz $x_{j}$ przez $x_{j}+\mu((x_{1}-x_{2})$ (jest tak, bo $F_{{ij}}||(x_{1}-x_{2})$ ). Zatem dobierając $\lambda=\frac{1}{2}$ oraz $\mu=-\frac{1}{2}$ dostaniemy ten sam wektor $w,$ i z warunku $F_{{ij}}=-F_{{ji}}$ wynika własność (4.6).

Dla układu $\mathcal{M}$ składającego się z $N$ punktów o położeniach $x_{i}\in{\bf R}$ oraz masach $m_{i}$ określmy środek masy $x_{0}$ tego układu za pomocą wzoru

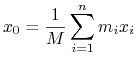$x_{0}=\frac{1}{M}\sum _{{i=1}}^{n}m_{i}x_{i}$

(4.7)

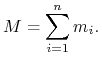
gdzie $\displaystyle{M=\sum _{{i=1}}^{n}m_{i}}.$

∎

Stwierdzenie 4.1

Dla układu $n-$ punktów położenie jego środka masy zmienia się tak, jak położenie punktu w ${\bf R}^{3}$ o masie $M$ na który działa siła $F=\sum _{{i=1}}^{n}F_{i}.$

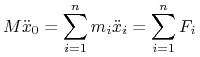
$M\ddot{x}_{0}=\displaystyle{\sum _{{i=1}}^{n}m_{i}\ddot{x}_{i}=\sum _{{i=1}}^{n}F_{i}}$

∎

Wniosek 4.1

Dla układu izolowanego jego środek masy porusza się ruchem jednostajnym prostoliniowym.

Na mocy (4.5) mamy wtedy $M\ddot{x}_{0}=0.$

∎

4.3. Układy potencjalne

Niech $\mathcal{M}$ będzie układem $n-$ punktów o maasach $m_{1},...,m_{n},$ którego przestrzeń fazowa $\mathcal{F}(\mathcal{M})$ ma współrzędne (4.1). Niech na punkty układu działają siły zewnętrzne oraz siły oddziaływania wzajemnego opisane przez macierz (4.4).

Definicja 4.3

Powiemy, że układ $\mathcal{M}$ jest potencjalny, jeżeli istnieje funkcja $U:\mathcal{F}(\mathcal{M})\rightarrow R$ zależna tylko od zmiennych $x_{1},...x_{n}$ taka, że (traktując $\mathcal{M}$ jako punkt przestrzeni ${\bf R}^{{3n}}$ ) siła działająca na ten punkt ma postać

$F(x_{1},...x_{n})=-grad\ U\ (x_{1},...x_{n}).$

(4.8)

Wtedy siła $F_{j}$ działająca na $j-$ ty punkt jest opisana jako $j-$ ta (wektorowa) współrzędna siły $F,$ tj

$F(x_{1},...x_{n})=\big(F_{1}(x_{1},...x_{n}),F_{2}(x_{1},...x_{n}),...,F_{n}(x_{1},...x_{n})\big)$

(4.9)

Definicja 4.4

Energią kinetyczną układu $\mathcal{M}$ nazwiemy funkcję $T:\mathcal{F}(\mathcal{M})\rightarrow R$ opisaną we współrzędnych (4.1) formułą

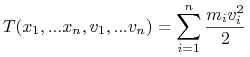$T(x_{1},...x_{n},v_{1},...v_{n})=\sum _{{i=1}}^{n}\frac{m_{i}v_{i}^{2}}{2}$

(4.10)

Niech na przestrzeni fazowej układu $\mathcal{M}$ dana będzie siła (4.9)(niekoniecznie potencjalna). Niech

$\dot{\gamma}:{\bf R}\ni t\rightarrow\big(x_{1}(t),x_{2}(t),...,x_{n}(t),\dot{x}_{1}(t),...,\dot{x}_{n}(t)\big)\in\mathcal{F}(\mathcal{M})$

(4.11)

gdzie

$m_{i}\ddot{x}_{i}(t)=F_{i}\big((x_{1}(t),...x_{n}(t)\big)i=1,2,..n.$

Stwierdzenie 4.2

Przyrost energii kinetycznej wzdłuż krzywej ruchu (LABEL:4.3.4) jest równy pracy siły (4.9) wzdłuż tej krzywej t.j. dla $t_{2}>t_{1}$

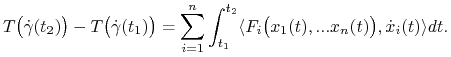$T\big(\dot{\gamma}(t_{2})\big)-T\big(\dot{\gamma}(t_{1})\big)=\displaystyle{\sum _{{i=1}}^{n}\int _{{t_{1}}}^{{t_{2}}}\langle F_{i}\big(x_{1}(t),...x_{n}(t)\big),\dot{x}_{i}(t)\rangle dt.}$

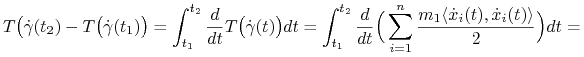$T\big(\dot{\gamma}(t_{2})-T\big(\dot{\gamma}(t_{1})\big)=\displaystyle{\int _{{t_{1}}}^{{t_{2}}}\frac{d}{dt}T\big(\dot{\gamma}(t)\big)dt=\int _{{t_{1}}}^{{t_{2}}}\frac{d}{dt}\Big(\sum _{{i=1}}^{n}\frac{m_{1}\langle\dot{x}_{i}(t),\dot{x}_{i}(t)\rangle}{2}\Big)dt}=$

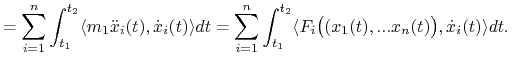$=\sum _{{i=1}}^{n}\int _{{t_{1}}}^{{t_{2}}}\langle m_{1}\ddot{x}_{i}(t),\dot{x}_{i}(t)\rangle dt=\sum _{{i=1}}^{n}\int _{{t_{1}}}^{{t_{2}}}\langle F_{i}\big((x_{1}(t),...x_{n}(t)\big),\dot{x}_{i}(t)\rangle dt.$

∎

Wniosek 4.2

Jeżeli siła $F$ jest potencjalna, to energia całkowita układu

$E(x_{1},...x_{n},v_{1},...v_{n})=T(v_{1},...v_{n})+U(x_{1},...x_{n})$

jest całką pierwszą ruchu.

Zauważmy, że w przypadku siły potencjalnej mamy

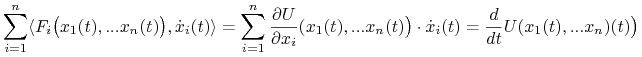$\sum _{{i=1}}^{n}\langle F_{i}\big(x_{1}(t),...x_{n}(t)\big),\dot{x}_{i}(t)\rangle=\sum _{{i=1}}^{n}\frac{\partial U}{\partial x_{i}}(x_{1}(t),...x_{n}(t)\big)\cdot\dot{x}_{i}(t)=\frac{d}{dt}U(x_{1}(t),...x_{n})(t)\big)$

zatem (porównaj dowód Stwierdzenia (4.3)).

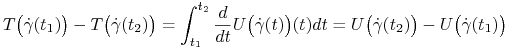$T\big(\dot{\gamma}(t_{1})\big)-T\big(\dot{\gamma}(t_{2})\big)=\int _{{t_{1}}}^{{t_{2}}}\frac{d}{dt}U\big(\dot{\gamma}(t)\big)(t)dt=U\big(\dot{\gamma}(t_{2})\big)-U\big(\dot{\gamma}(t_{1})\big)$

skąd wynika, że

$T\big(\dot{\gamma}(t_{1})\big)+U\big(\dot{\gamma}(t_{1})\big)=T\big(\dot{\gamma}(t_{2})\big)+U\big(\dot{\gamma}(t_{2})\big)$

∎

Stwierdzenie 4.3

Niech $\mathcal{M}$ będzie układem izolowanym z macierzą działających sił o postaci (4.4). Jeżeli siła $F_{{ij}}$ zależy tylko od odległości oddziaływujących punktów, t.j.

$F_{{ij}}(x_{1},...x_{n})=f_{{ij}}\big(|x_{i}-x_{j}|\big)\frac{x_{i}-x_{j}}{|x_{i}-x_{j}|}$

(4.12)

gdzie $f_{{ij}}:{\bf R}\rightarrow{\bf R}$ jest ciągła oraz $f_{{ij}}=f_{{ji}},$ to układ $\mathcal{M}$ jest potencjalny.

Niech $g_{{ij}}(t)=\int _{1}^{t}f_{{ij}}(s)ds$ będzie funkcją pierwotną funkcji $f_{{ij}}$ i niech $G_{{ij}}(x_{1},...x_{n})=g_{{ij}}(|x_{i}-x_{j}|)$ gdzie dla
$w=(w_{1},w_{2},w_{3})\ni{\bf R}^{3}.$ przyjmiemy

$|w|=\sqrt{w_{1}^{2}+w_{2}^{2}+w_{3}^{2}}$

Ponieważ dla $w=(w_{1},w_{2},w_{3}),\ \ v=((v_{1},v_{2},v_{3})$ zachodzi

$\frac{\partial}{\partial w_{i}}|w-v|=\frac{w_{i}-v_{i}}{|w-v|};\frac{\partial}{\partial v_{i}}=\frac{v_{i}-w_{i}}{|w-v|}$

(4.13)

$\frac{\partial}{\partial x_{k}}G_{{ij}}(x_{1},...x_{n})=\left\{\begin{array}[]{ll}0\ \ \ \textrm{jeżeli}\ k\neq i\ \textrm{oraz}\ k\neq j\\ \displaystyle{f_{{ij}}(|x_{i}-x_{j}|)\cdot\frac{x_{i}-x_{j}}{|x_{i}-x_{j}|}}&\textrm{jeżeli}\ k=i\\ \displaystyle{f_{{ij}}(|x_{i}-x_{j}|)\cdot\frac{x_{j}-x_{i}}{|x_{i}-x_{j}|}}&\textrm{jeżeli}\ k=j\end{array}\right.$

a zatem

$U(x_{1},...x_{n})=\sum _{{j.i}}G_{{ij}}(x_{1},...x_{n})$

jest potencjałem naszego układu.

∎

4.4. Zagadnienie dwóch ciał.

Przez zagadnienie n-ciał będziemy rozumieli problem rozwiązania równań opisujących ewolucję izolowanego i potencjalnego układu n-punktów materialnych. Zagadnienie to odegrało dużą rolę w rozwoju mechaniki. Pokazano, że dla $n\geq 3$ nie istnieje możliwość ”rozplątania” układu równań opisujących ruch i podania rozwiązania 'explicite'(rozwiązanie w kwadraturach). Dla dwóch punktów rozwiązanie takie istnieje. Istotnie, dla układu dwóch ciał o masach $m_{i}$ $m_{2}$ układ równań opisujący jego ewolucję ma zgodnie z Stwierdzeniem (4.3) postać

$\left\{\begin{array}[]{ll}m_{1}\ddot{x}_{1}(t)=-\frac{\partial}{\partial x_{1}}g_{{1.2}}(|x_{1}(t)-x_{2}(t)|)\\ m_{2}\ddot{x}_{2}(t)=-\frac{\partial}{\partial x_{2}}g_{{1.2}}(|x_{1}(t)-x_{2}(t)|)\\ \end{array}\right.$

(4.14)

gdzie $g:{\bf R}\rightarrow{\bf R}$ jest różniczkowalna.

Twierdzenie 4.2

Zmiana $x_{1}-x_{2}$ przy zagadnieniu dwóch ciał z potencjałem $U_{{1,2}}$ odbywa się tak, jak zmiana położenia ruchu pojedynczego punktu o masie $\displaystyle{\frac{m_{1}m_{2}}{m_{1}+m_{2}}}$ w $\bf R^{3}$ pod wpływem potencjału $V(x)=g_{{1,2}}(|x|).$

Mnożąc pierwsze z równań (4.4.1) przez $m_{2}$ a drugie przez $m_{1}$ i odejmując stronami otrzymamy (porównaj (4.13))

$m_{1}m_{2}(x_{1}\ddot{-}x_{2})=m_{2}\frac{\partial}{\partial x_{1}}g_{{1,2}}(|x_{1}-x_{2}|)-m_{1}\frac{\partial}{\partial x_{2}}g_{{1,2}}(|x_{1}-x_{2}|)=$

$=m_{2}\frac{dg_{{1,2}}}{dt}(|x_{1}-x_{2}|)\cdot\frac{x_{1}-x_{2}}{|x_{1}-x_{2}|}+m_{1}\frac{dg_{1}}{dt}(|x_{1}-x_{2}|)\cdot\frac{x_{1}-x_{2}}{|x_{1}-x_{2}|}=$

$=-(m_{1}+m_{2})\frac{dg_{{1,2}}}{dt}(|x_{1}-x_{2}|)\cdot\frac{x_{1}-x_{2}}{|x_{1}-x_{2}|}$

A zatem dla $x=x_{1}-x_{2}$ otrzymamy

$\frac{m_{1}\cdot m_{2}}{(m_{1}+m_{2})}\ddot{x}=-\frac{dg_{{1,2}}}{dt}(|x|)\frac{x}{|x|}=-\frac{\partial}{\partial x}g_{{1,2}}(|x|).$

Niech $x_{0}=\frac{m_{1}x_{1}+m_{2}x_{2}}{m_{1}+m_{2}}$ będzie środkiem masy naszego układu oraz niech $x=x_{1}-x_{2}.$ Wtedy

$x_{1}=x_{0}+\frac{m_{2}}{m_{1}+m_{2}}x$

$x_{2}=x_{0}-\frac{m_{1}}{m_{1}+m_{2}}x$

a zatem, zgodnie z wnioskiem 4.2.4 otrzymamy $x_{0}(t)+x_{0}+v_{0}t$ i dla wyznaczenia $x_{1}$ oraz $x_{2}$ wystarczy znależć $x(t)$ , tj podać opis ruchu punktu w $\bf R^{3}$ pod wpływem danego potencjału o postaci $U(x)=f(|x|).$ Zagadnienie to posiada rozwiązanie, które podamy w następnym wykładzie.

∎