Zagadnienia
4. Symetrie i całki pierwsze
4.1. Pęd i moment pędu
Omówimy teraz kilka typowych przykładów symetrii w układach mechanicznych. Przez symetrię rozumiemy tu dodatkowe warunki, jakie spełniają siły występujące w rozważanym układzie mechanicznym.
Pierwszym takim warunkiem zaobserwowanym w poprzednim wykładzie (dla układu jednopunktowego) jest potencjalność występującej siły. Konsekwencją tej symetrii jest pojawienie się całki pierwszej - energii całkowitej rozpatrywanego punktu.
W dalszym tekście wygodnie będzie traktować układ n-punktów w ![]() jako jeden punkt w
jako jeden punkt w ![]() . Jak zauważyliśmy w Wykładzie 3 przestrzeń fazową
. Jak zauważyliśmy w Wykładzie 3 przestrzeń fazową ![]() takiego układu, którą jest wiązka styczna do
takiego układu, którą jest wiązka styczna do ![]() możemy utożsamiać z
możemy utożsamiać z ![]() t.j.
t.j. ![]()
Punkt przestrzeni ![]() ma wtedy współrzędne
ma wtedy współrzędne
| (4.1) |
gdzie ![]() jest położeniem
jest położeniem ![]() tego punktu a
tego punktu a ![]() jest jego prędkością.
jest jego prędkością.
Definicja 4.1
(a) Niech ruch punktu materialnego o masie ![]() opisany będzie krzywą gładką
opisany będzie krzywą gładką ![]() . Pędem tego punktu w chwili
. Pędem tego punktu w chwili ![]() nazwiemy
nazwiemy ![]()
(b) Niech ruch układu ![]()
![]() punktów o masach
punktów o masach ![]() opisany będzie krzywą w przestrzeni fazowej
opisany będzie krzywą w przestrzeni fazowej ![]()
Pędem tego układu w chwili ![]() nazwiemy wektor
nazwiemy wektor
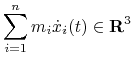 |
(4.2) |
(c) Dla punktu materialnego (a) jego momentem pędu w chwili ![]() nazwiemy wektor
nazwiemy wektor
gdzie ![]() oznacza iloczyn wektorowy wektorów
oznacza iloczyn wektorowy wektorów ![]()
(d) Dla układu ![]() z punktu
z punktu ![]() momentem pędu tego układu w chwili
momentem pędu tego układu w chwili ![]() nazwiemy wektor
nazwiemy wektor
![\sum _{{i=1}}^{n}\big[x_{i}(t),m_{i}\dot{x}(t)\big]\in{\bf R}^{3}](wyklady/mmk/mi/mi251.png) |
(4.3) |
Uwaga 4.1
(a) Zarówno w przypadku pędu jak i momentu pędu mamy do czynienia z następującą sytuacją. Na przestrzeni fazowej ![]() są określone funkcje
są określone funkcje
![]() zwana pędem oraz
zwana pędem oraz
![]() zwana momentem pędu
zwana momentem pędu
takie, że formuły (4.2) i (4.3) otrzymamy jako superpozycje odpowiednio ![]() i
i ![]()
(b) Można rozważać także moment pędu względem ustalonego punktu ![]() dany formułą
dany formułą ![]() z podobną zmianą formuły (4.3).
z podobną zmianą formuły (4.3).
4.2. Układy izolowane
Niech dany będzie układ n-punktów. Siłę ![]() działającą na
działającą na ![]() ty punkt można zapisać w postaci
ty punkt można zapisać w postaci
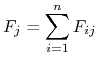 |
gdzie ![]() dla
dla ![]() jest siłą z jaką
jest siłą z jaką ![]() ty punkt oddziaływuje na
ty punkt oddziaływuje na ![]() ty, natomiast
ty, natomiast ![]() jest siłą działającą na
jest siłą działającą na ![]() ty punkt z zewnątrz. Będziemy przy tym zakładać, że siła
ty punkt z zewnątrz. Będziemy przy tym zakładać, że siła ![]() jest równoległa do wektora
jest równoległa do wektora ![]() , gdzie
, gdzie ![]() jest położeniem
jest położeniem ![]() tego punktu.
tego punktu.
Otrzymujemy zatem opis działających sił w formie macierzy
| (4.4) |
gdzie siłę działającą na punkt ![]() ty otrzymujemy jako sumę sił występujących w
ty otrzymujemy jako sumę sił występujących w ![]() tej kolumnie.
tej kolumnie.
Definicja 4.2
Układ n-punktów nazwiemy izolowanym, jeżeli macierz ![]() jest antysymetryczna, tj. jeżeli
jest antysymetryczna, tj. jeżeli ![]() Warunek ten zawiera dwa ważne warunki częściowe. Po pierwsze siła zewnętrzna
Warunek ten zawiera dwa ważne warunki częściowe. Po pierwsze siła zewnętrzna ![]() działająca na
działająca na ![]() ty punkt jest zerowa.
ty punkt jest zerowa.
Po drugie suma wszystkich sił działających na punkty tworzące układ jest zerowa, tj
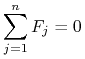 |
(4.5) |
Twierdzenie 4.1
Dla układów izolowanych pęd układu ![]() oraz moment pędu układu
oraz moment pędu układu ![]() są całkami pierwszymi ruchu.
są całkami pierwszymi ruchu.
Niech
będzie krzywą ruchu w przestrzeni fazowej ![]() rozważanego układu.
rozważanego układu.
Mamy pokazać, że
![(P\circ\dot{\gamma})(t)=\sum _{{i=1}}^{n}m_{i}\dot{x}_{i}(t)\ \ \ \textrm{oraz}\ \ (M\circ\dot{\gamma})(t)=\sum _{{i=1}}^{n}\big[x_{i}(t),m_{i}\dot{x}_{i}(t)\big],](wyklady/mmk/mi/mi300.png) |
gdzie ![]() jest masą
jest masą ![]() tego punktu, są całkami pierwszymi.
tego punktu, są całkami pierwszymi.
Na mocy warunku (4.5) mamy
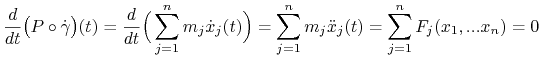 |
Podobnie wykorzystując (4.5) oraz własność ![]() dla
dla ![]() otrzymamy
otrzymamy
![\frac{d}{dt}\big(M\circ\dot{\gamma}\big)(t)=\frac{d}{dt}\Big(\sum _{{j=1}}^{n}\big[x_{j}(t),m_{j}\dot{x}_{j}(t)\big]\Big)=](wyklady/mmk/mi/mi281.png) |
![=\sum _{{j=1}}^{n}\Big(\big[\dot{x}_{j}(t),m_{j}\dot{x}_{j}(t)\big]+\big[x_{j}(t),m_{j}\ddot{x}_{j}(t)\big]\Big)=\sum _{{j=1}}^{n}\big[x_{j}(t),F_{j}(x_{1},...x_{n})\big]=](wyklady/mmk/mi/mi298.png) |
![=\sum _{{j=1}}^{n}\big[x_{j}(t),\sum _{{i=1}}^{n}F_{{ij}}(x_{1},...x_{n})\big]=\sum _{{ij=1}}^{n}\big[x_{j}(t)F_{{ij}}(x_{1},...x_{n})\big]](wyklady/mmk/mi/mi334.png) |
Wykorzystując antysymetrię macierzy sił ![]() możemy ostatnią sumę zapisać jako sumę po wszystkich parach
możemy ostatnią sumę zapisać jako sumę po wszystkich parach ![]() podwójnych indeksów, gdzie drugi podwójny indeks otrzymujemy przez transpozycję pierwszego. Pokażemy, że wynik sumowania w każdej takiej parze daje zero, t.j., że
podwójnych indeksów, gdzie drugi podwójny indeks otrzymujemy przez transpozycję pierwszego. Pokażemy, że wynik sumowania w każdej takiej parze daje zero, t.j., że
| (4.6) |
Istotnie, z własności iloczynu wektorowego wynika, że w obydwu składnikach sumy w (4.6) możemy zastąpić odpowiednio ![]() przez
przez ![]() oraz
oraz ![]() przez
przez ![]() (jest tak, bo
(jest tak, bo ![]() ). Zatem dobierając
). Zatem dobierając ![]() oraz
oraz ![]() dostaniemy ten sam wektor
dostaniemy ten sam wektor ![]() i z warunku
i z warunku ![]() wynika własność (4.6).
wynika własność (4.6).
Dla układu ![]() składającego się z
składającego się z ![]() punktów o położeniach
punktów o położeniach ![]() oraz masach
oraz masach ![]() określmy środek masy
określmy środek masy ![]() tego układu za pomocą wzoru
tego układu za pomocą wzoru
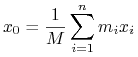 |
(4.7) |
gdzie 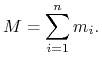
Stwierdzenie 4.1
Dla układu ![]() punktów położenie jego środka masy zmienia się tak, jak położenie punktu w
punktów położenie jego środka masy zmienia się tak, jak położenie punktu w ![]() o masie
o masie ![]() na który działa siła
na który działa siła ![]()
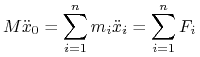
Wniosek 4.1
Dla układu izolowanego jego środek masy porusza się ruchem jednostajnym prostoliniowym.
Na mocy (4.5) mamy wtedy ![]()
4.3. Układy potencjalne
Niech ![]() będzie układem
będzie układem ![]() punktów o maasach
punktów o maasach ![]() którego przestrzeń fazowa
którego przestrzeń fazowa ![]() ma współrzędne (4.1). Niech na punkty układu działają siły zewnętrzne oraz siły oddziaływania wzajemnego opisane przez macierz (4.4).
ma współrzędne (4.1). Niech na punkty układu działają siły zewnętrzne oraz siły oddziaływania wzajemnego opisane przez macierz (4.4).
Definicja 4.3
Powiemy, że układ ![]() jest potencjalny, jeżeli istnieje funkcja
jest potencjalny, jeżeli istnieje funkcja ![]() zależna tylko od zmiennych
zależna tylko od zmiennych ![]() taka, że (traktując
taka, że (traktując ![]() jako punkt przestrzeni
jako punkt przestrzeni ![]() ) siła działająca na ten punkt ma postać
) siła działająca na ten punkt ma postać
| (4.8) |
Wtedy siła ![]() działająca na
działająca na ![]() ty punkt jest opisana jako
ty punkt jest opisana jako ![]() ta (wektorowa) współrzędna siły
ta (wektorowa) współrzędna siły ![]() tj
tj
| (4.9) |
Definicja 4.4
Energią kinetyczną układu ![]() nazwiemy funkcję
nazwiemy funkcję ![]() opisaną we współrzędnych (4.1) formułą
opisaną we współrzędnych (4.1) formułą
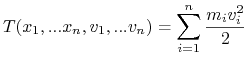 |
(4.10) |
Niech na przestrzeni fazowej układu ![]() dana będzie siła (4.9)(niekoniecznie potencjalna). Niech
dana będzie siła (4.9)(niekoniecznie potencjalna). Niech
| (4.11) |
gdzie
Stwierdzenie 4.2
Przyrost energii kinetycznej wzdłuż krzywej ruchu (LABEL:4.3.4) jest równy pracy siły (4.9) wzdłuż tej krzywej t.j. dla ![]()
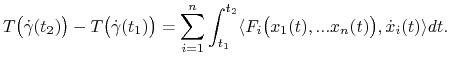 |
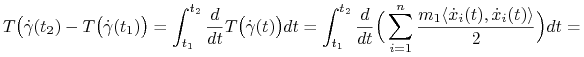 |
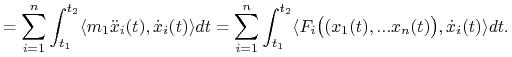 |
Wniosek 4.2
Jeżeli siła ![]() jest potencjalna, to energia całkowita układu
jest potencjalna, to energia całkowita układu
jest całką pierwszą ruchu.
Zauważmy, że w przypadku siły potencjalnej mamy
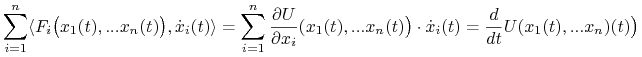 |
zatem (porównaj dowód Stwierdzenia (4.3)).
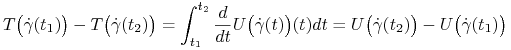 |
skąd wynika, że
Stwierdzenie 4.3
Niech ![]() będzie układem izolowanym z macierzą działających sił o postaci (4.4). Jeżeli siła
będzie układem izolowanym z macierzą działających sił o postaci (4.4). Jeżeli siła ![]() zależy tylko od odległości oddziaływujących punktów, t.j.
zależy tylko od odległości oddziaływujących punktów, t.j.
| (4.12) |
gdzie ![]() jest ciągła oraz
jest ciągła oraz ![]() to układ
to układ ![]() jest potencjalny.
jest potencjalny.
Niech ![]() będzie funkcją pierwotną funkcji
będzie funkcją pierwotną funkcji ![]() i niech
i niech ![]() gdzie dla
gdzie dla ![]() przyjmiemy
przyjmiemy
Ponieważ dla ![]() zachodzi
zachodzi
| (4.13) |
to
![\frac{\partial}{\partial x_{k}}G_{{ij}}(x_{1},...x_{n})=\left\{\begin{array}[]{ll}0\ \ \ \textrm{jeżeli}\ k\neq i\ \textrm{oraz}\ k\neq j\\
\displaystyle{f_{{ij}}(|x_{i}-x_{j}|)\cdot\frac{x_{i}-x_{j}}{|x_{i}-x_{j}|}}&\textrm{jeżeli}\ k=i\\
\displaystyle{f_{{ij}}(|x_{i}-x_{j}|)\cdot\frac{x_{j}-x_{i}}{|x_{i}-x_{j}|}}&\textrm{jeżeli}\ k=j\end{array}\right.](wyklady/mmk/mi/mi317.png) |
a zatem
jest potencjałem naszego układu.
∎4.4. Zagadnienie dwóch ciał.
Przez zagadnienie n-ciał będziemy rozumieli problem rozwiązania równań opisujących ewolucję izolowanego i potencjalnego układu n-punktów materialnych. Zagadnienie to odegrało dużą rolę w rozwoju mechaniki. Pokazano, że dla ![]() nie istnieje możliwość ”rozplątania” układu równań opisujących ruch i podania rozwiązania 'explicite'(rozwiązanie w kwadraturach).
Dla dwóch punktów rozwiązanie takie istnieje. Istotnie, dla układu dwóch ciał o masach
nie istnieje możliwość ”rozplątania” układu równań opisujących ruch i podania rozwiązania 'explicite'(rozwiązanie w kwadraturach).
Dla dwóch punktów rozwiązanie takie istnieje. Istotnie, dla układu dwóch ciał o masach ![]()
![]() układ równań opisujący jego ewolucję ma zgodnie z Stwierdzeniem (4.3) postać
układ równań opisujący jego ewolucję ma zgodnie z Stwierdzeniem (4.3) postać
![\left\{\begin{array}[]{ll}m_{1}\ddot{x}_{1}(t)=-\frac{\partial}{\partial x_{1}}g_{{1.2}}(|x_{1}(t)-x_{2}(t)|)\\
m_{2}\ddot{x}_{2}(t)=-\frac{\partial}{\partial x_{2}}g_{{1.2}}(|x_{1}(t)-x_{2}(t)|)\\
\end{array}\right.](wyklady/mmk/mi/mi274.png) |
(4.14) |
gdzie ![]() jest różniczkowalna.
jest różniczkowalna.
Twierdzenie 4.2
Zmiana ![]() przy zagadnieniu dwóch ciał z potencjałem
przy zagadnieniu dwóch ciał z potencjałem ![]() odbywa się tak, jak zmiana położenia ruchu pojedynczego punktu o masie
odbywa się tak, jak zmiana położenia ruchu pojedynczego punktu o masie ![]() w
w ![]() pod wpływem potencjału
pod wpływem potencjału ![]()
Mnożąc pierwsze z równań (4.4.1) przez ![]() a drugie przez
a drugie przez ![]() i odejmując stronami otrzymamy (porównaj (4.13))
i odejmując stronami otrzymamy (porównaj (4.13))
A zatem dla ![]() otrzymamy
otrzymamy
Niech ![]() będzie środkiem masy naszego układu oraz niech
będzie środkiem masy naszego układu oraz niech ![]() Wtedy
Wtedy
a zatem, zgodnie z wnioskiem 4.2.4 otrzymamy ![]() i dla wyznaczenia
i dla wyznaczenia ![]() oraz
oraz ![]() wystarczy znależć
wystarczy znależć ![]() , tj podać opis ruchu punktu w
, tj podać opis ruchu punktu w ![]() pod wpływem danego potencjału o postaci
pod wpływem danego potencjału o postaci ![]() Zagadnienie to posiada rozwiązanie, które podamy w następnym wykładzie.
Zagadnienie to posiada rozwiązanie, które podamy w następnym wykładzie.




