Zagadnienia

5.1 Pola centralne
5.2 Ruch w polu centralnym w ${\bf R^{2}}$
5.3 Całkowanie równań ruchu w polu centralnym w ${\bf R^{2}}$

5. Symetria sferyczna w 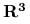${\bf R^{3}}$

5.1. Pola centralne

Definicja 5.1

Polem centralnym w ${\bf R}^{3}$ nazwiemy pole wektorowe $F$ na ${\bf R}^{n}\backslash\{{0}\}$ o postaci

$F(x)=f(|x|)\frac{x}{|x|}$

(5.1)

gdzie $f:{\bf R}^{{+}}\rightarrow\bf R$ jest funkcją ciągłą a $\displaystyle{|x|={<x,x>}^{\frac{1}{2}}}.$ Pole (5.1) jest zawsze potencjalne z potencjałem $V(x)=g(|x|)$ gdzie $g$ jest funkcją pierwotną $f$ . (Porównaj dowód Swierdzenia 4.3.).

Definicja 5.2

Grupą ortogonalną $O(n,{\bf R})$ nazwiemy grupę przekształceń liniowych, scharakteryzowanych warunkiem: $A\in O(n,\bf{R})$ wtedy i tylko wtedy, kiedy

$\left\langle A(x),A(y)\right\rangle=\left\langle x,y\right\rangle\ \textrm{dla}\ \ x,y\in{\bf R}^{n}$

(5.2)

Warunek ten jest równoważny warunkowi podającemu opis macierzy przekształceń liniowych tworzących $O(n,\bf{R}):$ $A\in O(n,\bf{R})$ wtedy i tylko wtedy, kiedy macierz $\big[A\big]$ tego przekształcenia względem dowolnej bazy ortonormalnej spełnia warunek

$\big[A\big]^{{-1}}=\big[A\big]^{t}$

(5.3)

gdzie $\big[A\big]^{t}$ oznacza macież transponowaną do $\big[A\big].$

Stwierdzenie 5.1

Pole centralne (5.1) jest niezmiennicze dla naturalnego działania w ${\bf R}^{n}\backslash\{{0}\}$ grupy przekształceń ortogonalnych $O(n,{\bf R}).$ Oznacza to, że dla każdego
$A\in O(n,\bf R)$ oraz dla każdego $x\in{\bf R}^{n}\ \big\{{0}\big\}$ zachodzi

$F\big(A(x)\big)=\big(d_{x}A\big)\big(F(x)\big)$

(5.4)

Dla przekształcenia liniowego $B$ jego różniczka w dowolnym punkcie jest równa $B.$ Zatem z (5.1) dla $A\in O(n,\bf{R})$ oraz $x\in{\bf R}^{n}$ wynika

$F\big(A(x))\big)=f\big(|A(x)|\big)\frac{A(x)}{|A(x)|}=\frac{f(|x|)}{|x|}A(x)=A\big(F(x)\big)=\big(d_{x}A\big)\big(F(x)\big)$

Wykorzystaliśmy tu równość $|A(x)|=|x|$ wynikającą z (5.2).

∎

Stwierdzenie 5.2

Dla pola centralnego w ${\bf R^{3}}$ moment pędu $M$ jest całką pierwszą.

Niech $\bf{R}\ni t\rightarrow x(t)\in{\bf R}^{3}\backslash\big\{ 0\big\}$ będzie ruchem punktu o masie $m$ pod działaniem centralnej siły $F.$ Niech $\big[\cdot,\cdot\big]$ oznacza iloczyn wektorowy w $\bf{R}^{3}.$ Wtedy

$\frac{d}{dt}\ M(t)=\frac{d}{dt}\big[x(t),m\dot{x}(t)\big]=\big[\dot{x}(t),m\dot{x}(t)\big]+\big[x(t),m\ddot{x}(t)\big]=\big[x(t),F\big(x(t)\big)\big]=0$

bo wektor $F\big(x(t)\big)$ jest proporcjonalny do $x(t).$

∎

Wniosek 5.1

Ruch w polu centralnym w ${\bf R}^{3}$ jest płaski. Dokładniej:

(A) Jeżeli $\big[x(0),m\dot{x}(0)\big]=M(0)\neq 0$ to ruch odbywa się w płaszczyźnie.

$N=\big\{ y\in{\bf R}^{3}:\langle y,M(0)\rangle=0\big\},$

(5.5)

którą też można opisać jako płaszczyznę rozpinaną przez $x(0)$ oraz $\dot{x}(0).$

(B) Jeżeli $M(0)=0$ to ruch odbywa się po prostej zawierającej $0$ oraz $x(0).$

(A) Ze stałości $M(t)$ wynika, że $[x(t),m\dot{x}(t)]=M(0).$ Zatem $x(t)\perp M(0)$ dla każdego $t$ . Ponadto $x(0)$ i $\dot{x}(0)$ należą do $N$ i nie są współliniowe.

(B) Jeżeli $M(0)=M(t)=0$ to $\dot{x}(t)||x(t)$ czyli

$\dot{x}(t)=a(t)x(t),$

(5.6)

gdzie funkcja $a:\bf R\rightarrow\bf R$ jest różniczkowalna ( bo $t\rightarrow x(t)$ ) jest dwukrotnie różniczkowalna). Niech $b:\bf R\rightarrow\bf{R}^{+}$ będzie funkcją różniczkowalną. Wtedy funkcja wektorowa $y(t)=b(t)x(0)$ spełnia warunek

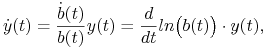$\dot{y}(t)=\frac{\dot{b}(t)}{b(t)}y(t)=\frac{d}{dt}ln\big(b(t)\big)\cdot{y}(t),$

który dla $b_{0}(t)=e^{{\int _{{1}}^{{t}}a(s)ds}}$ przechodzi na (5.6). Z twierdzenia o jednoznaczności mamy więc

$x(t)=b_{0}(t)x(0).$

∎

Wniosek 5.2

Niech $F$ będzie polem centralnym w $\bf{R}^{3},$ a $V$ podprzestrzenią w $\bf{R}^{3},$ rozpiętą przez dwie pierwsze osie współrzędnych. Każdą trajektorię ruchu w polu $F$ można uzyskać jako obraz pewnej trajektorii tego pola, leżącej w $V,$ za pomocą pewnego przekształcenia $A\in O(3\bf R).$

Niech

$\bf{R}\ni t\rightarrow\gamma(t)\in\bf{R}^{3}$

będzie krzywą ruchu dla pola $F.$ Rozpatrzmy przypadek kiedy

$M(0)=\big[\gamma(0),m\dot{\gamma}(0)\big]\neq 0.$

Przypadek $M(0)=0$ zostawimy jako zadanie czytelnikowi.
Niech $A\in O(3,\bf R)$ będzie takim przekształceniem ortogonalnym , że

$A\big((0,0,|M(0)|)\big)=M(0).$

Wtedy $A(V)=N$ ( $N$ jak w (5.5)). Niech

$x_{0}=A^{{-1}}\big(\gamma(0)\big)y_{0}=A^{{-1}}\big(\dot{\gamma}(0)\big)$

i niech $\delta(t)$ będzie krzywą ruchu w polu $F$ wyznaczoną przez warunki początkowe $\delta(0)=x_{0}$ , $\dot{\delta}=y_{0}.$ Wtedy $\delta(t)\in V$ oraz $\gamma(t)=A\big(\delta(t)\big).$

∎

Wniosek 5.3

Każdy ruch w polu centralnym ${\bf R}^{3}$ jest izometrycznie równoważny pewnemu ruchowi w polu centralnym w ${\bf R}^{2}.$

Każde pole centralne w ${\bf R}^{2}$ powstaje przez ograniczenie do przestrzeni $V\simeq{\bf R}^{2}$ pewnego pola centralnego w ${\bf R}^{3}$ - i odwrotnie - każde takie pole jest wyznaczone przez swoje ograniczenie do $V.$

∎

5.2. Ruch w polu centralnym w 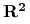${\bf R^{2}}$

Zaczniemy od sformułowania analogii Stwierdzenia 5.2 dla ruchu w centralnym polu w ${\bf R^{2}}.$ Dla uproszczenia, w dalszej części tego punktu przyjmiemy, że $m=1.$ Zanurzając ${\bf R}^{2}$ jako przestrzeń $V$ w ${\bf R}^{3}$ rozważmy ruch $x(t)=\big(x_{1}(t),x_{2}(t),0\big)$ w ${\bf R}^{3}.$ Wtedy

$\big[x(t),\dot{x}(t)\big]=\big(0,0,x_{1}(t)\dot{x}_{2}(t)-x_{2}(t)\dot{x}_{1}(t)\big).$

Zatem funkcja

$M(t)=x_{1}(t)\dot{x}_{2}(t)-x_{2}(t)\dot{x}_{1}(t)$

(5.7)

jest (skalarną) całką pierwszą ruchu w polu centralnym w $\bf{R}^{2}.$ Nadamy tej funkcji sens geometryczny, przechodząc do współrzędnych biegunowych $r,\varphi.$ Wtedy

$x_{1}(t)=r(t)\cos\varphi(t)$

$x_{2}(t)=r(t)\sin\varphi(t)$

a zatem

$\dot{x}_{1}(t)=\dot{r}(t)\cos\varphi(t)-r(t)\sin\varphi(t)\cdot\dot{\varphi}(t)$

$\dot{x}_{2}(t)=\dot{r}(t)\sin\varphi(t)+r(t)\cos\varphi(t)\cdot\dot{\varphi}(t)$

i otrzymamy

$M(t)=r(t)\cos\varphi(t)\big(\dot{r}(t)\sin\varphi(t)+r(t)\cos\varphi(t)\cdot\dot{\varphi}(t)\big)-$

$-r(t)\sin\varphi(t)\big(\dot{r}(t)\cos\varphi(t)-r(t)\sin\varphi(t)\cdot\dot{\varphi}(t)\big)=r^{2}(t)\dot{\varphi}(t)$

Widzimy, że wyrażenie (5.7) przyjmie we współrzędnych biegunowych postać

$M(t)=M\big(r(t),\varphi(t)\big)=r^{2}(t)\cdot\dot{\varphi}(t).$

(5.8)

Stwierdzenie 5.3

Dla ruchu w polu centralnym w ${\bf R}^{2}$ opisanym za pomocą współrzędnych biegunowych zachodzi

$M(t)=2\frac{dP}{dt}(t)$

(5.9)

gdzie

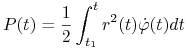$P(t)=\frac{1}{2}\int _{{t_{1}}}^{t}r^{2}(t)\dot{\varphi}(t)dt$

(5.10)

oznacza pole sektora ograniczonego promieniami $\varphi(t_{1}),\varphi(t)$ oraz krzywą ruchu $r(t)=r\big({\varphi}(t)\big).$ Wielkość $\displaystyle{\frac{dP}{dt}(t)}$ nazywamy prędkością polową.

Ponieważ w przypadku koła o promieniu r pole wycinka kołowego opartego na łuku o kącie środkowym $\triangle\varphi$ wynosi

$\triangle P=\pi r^{2}\cdot\frac{\triangle\varphi}{2\pi}=\frac{1}{2}r^{2}\triangle\varphi$

to pole sektora krzywoliniowego ograniczonego promieniami $\varphi _{1}$ i $\varphi$ oraz krzywą $r(\varphi)$ otrzymamy jako

$P(\varphi)=\frac{1}{2}\int _{{\varphi _{1}}}^{{\varphi}}r^{2}(\varphi)d\varphi$

(5.11)

Zakładamy, że funkcja $\varphi\rightarrow r(\varphi)$ jest ciągła na przedziale $\big[\varphi _{1},\varphi\big].$ Jeżeli zarówno $r$ jak $\varphi$ są funkcjami $t$ i przy tym $\varphi$ jest monotoniczna, $P(\varphi)$ przechodzi na (5.10) i wtedy

$r^{2}(t)\dot{\varphi}(t)=2\frac{dP(t)}{dt}.$

∎

Wniosek 5.4

Ruch w polu centralnym w $\bf{R}^{3}$ odbywa się w płaszczyźnie w taki sposób, że jego prędkość polowa względem centrum jest stała.

Reguła ta została doświadczalnie wykryta przez Keplera dla ruchu Marsa wokół Słońca.

5.3. Całkowanie równań ruchu w polu centralnym w ${\bf R^{2}}$

Ponieważ siła w polu centralnym w każdym punkcie jest skierowana radialnie, wygodnie będzie opisywać ruch, rozkładając w każdej chwili występujące wektory względem zmiennego układu ortogonalnego $e_{r},e_{{\varphi}}$ w taki sposób ,że dla punktu o współrzędnych biegunowych $r(t),\varphi(t)$ stosowany w chwli t układ będzie miał postać:

$e_{r}(t)=\big(\cos\varphi(t),\sin\varphi(t)\big)$

$e_{{\varphi}}(t)=\big(-\sin\varphi(t),\cos\varphi(t)\big)$

Ostrzeżenie Obserwowana poprzez liczenie pochodnych zmiana w czasie dotyczy układu nieruchomego i te pochodne dopiero po ich policzeniu rozkładamy względem zmieniającej się w czasie bazy.

Zaczniemy od obliczenia pochodnych funkcji $t\rightarrow e_{r}(t)$ i $t\rightarrow e_{\varphi}(t)$ i przedstawieniu ich w układzie ruchomym. I tak

$\left\{\begin{array}[]{ll}\dot{e}_{{r}}(t)=\big(-\sin\varphi(t)\dot{\varphi}(t)\cos\varphi(t)\dot{\varphi}(t)\big)=\dot{\varphi}(t)e_{{\varphi}}(t)&\\ \par \dot{e}_{{\varphi}}(t)=\big(-\cos\varphi _{{(t)}}\dot{\varphi}(t),-\sin\varphi(t)\dot{\varphi}(t)\big)=-\dot{\varphi}(t)e_{r}(t)&\end{array}\right.$

(5.12)

(W dalszym ciągu dla większej przejrzystości długich wzorów zrezygnujemy z pisania explicite argumentu $t.$ Zatem napiszemy $\varphi$ zamiast $\varphi(t)$ , podobnie $\dot{\varphi}$ zamiast $\dot{\varphi}(t)$ i tak dalej.)

Pisząc $x(t)=r(t)e_{{r}}(t)$ i stosując (5.12) otrzymamy

$\dot{x}=\displaystyle{\dot{r}e_{r}+r\dot{e}_{{r}}=\dot{r}e_{{r}}+r\dot{\varphi}e_{{\varphi}}}$

$\ddot{x}=\ddot{r}e_{r}+\dot{r}\dot{\varphi}e_{\varphi}+\dot{r}\dot{\varphi}e_{\varphi}+r\ddot{\varphi}{e}_{\varphi}-r\dot{\varphi}^{2}e_{r}=(\ddot{r}-\dot{r}\dot{\varphi}^{2})e_{r}+(2\dot{r}\dot{\varphi}+r\ddot{\varphi})e_{{\varphi}}$

Ponieważ $F(x)=f(r)e_{{r}},$ otrzymamy stąd dwa równania

$\left\{\begin{array}[]{ll}\ddot{r}-r\dot{\varphi}^{2}=f(r)&\\ 2\dot{r}\dot{\varphi}+r\ddot{\varphi}=0&\end{array}\right.$

(5.13)

Zauważmy, że zasada stałości prędkości polowej oznacza, że

$\frac{d}{dt}\big(r^{2}\dot{\varphi}\big)=0$

(5.14)

czyli

$r\big(2\dot{r}\dot{\varphi}+r\dot{\varphi}\big)=0$

a zatem drugie z równań (5.13) jest równoważne warunkowi (5.14), który jest równoważny równości $mr^{2}\dot{\varphi}=M.$ $M$ jest stałą zależną od warunków początkowych, którą dla zwięzłości nazwiemy momentem pędu. Zatem

$\dot{\varphi}=\frac{M}{mr^{2}}$

(5.15)

Wstawiając (5.15) do pierwszego z równań (5.13) sprowadzamy je do postaci zawierającej tylko funkcję $r(t)$ i jej pochodne:

$m\ddot{r}=f(r)+\frac{M^{2}}{mr^{3}}$

(5.16)

Podsumujemy nasze rozważania tak:

Stwierdzenie 5.4

Odległość od środka układu w ruchu centralnym w ${\bf R}^{2}$ z momentem pędu $M$ i potencjałem $V(x,y)=g(r)$ zmienia się jak odległość od zera w jednowymiarowym ruchu z potencjałem

$U(r)=g(r)+\frac{M^{2}}{2mr^{2}}$

(5.17)

Istotnie, możemy przepisać (5.16) w postaci

$m\ddot{r}=-\frac{d}{dr}g(r)+\frac{M^{2}}{mr^{3}}=-\frac{d}{dr}\big(g(r)+\frac{M^{2}}{2mr^{2}}\big)$

(5.18)

∎

Stwierdzenie 5.5

Energia całkowita w ruchu dwuwymiarowym z ustalonym momentem pędu $M$ jest taka sama, jak dla ruchu jednowymiarowego z potencjałem (5.17).

W ruchu z potencjałem (5.17) otrzymamy

$E_{{1}}=\frac{m\dot{r}^{2}}{2}+g(r)+\frac{M^{2}}{2mr^{2}}$

(5.19)

natomiast w ruchu dwuwymiarowym, kiedy $x=re_{r},$ mamy $\dot{x}=\dot{r}e_{r}+r\dot{\varphi}e_{{\varphi}}$ a więc dla $\displaystyle{\dot{\varphi}=\frac{M}{mr^{2}}}$ otrzymamy energię kinetyczną w postaci

$T(\dot{x})=\frac{1}{2}m\dot{x}^{2}=m\big(\dot{r}^{2}+r^{2}\dot{\varphi}^{2}\big)=\frac{m}{2}\big(\dot{r}^{2}+\frac{r^{2}M^{2}}{m^{2}r^{4}}\big)=\frac{m\dot{r}^{2}}{2}+\frac{M^{2}}{2mr^{2}}.$

Aby podać explicite rozwiązanie równań (5.13) posłużymy się jeszcze jedną całką prostą, jaką jest energia całkowita (5.19). Z (5.19) wynika, że przy ustalonych energii całkowitej $E$ oraz momencie pędu $M$ mamy

$\Big(\frac{dr}{dt}\Big)^{2}=\frac{2}{m}\Big(E-g(r)-\frac{{M}^{2}}{2mr^{2}}\Big)$

skąd

$t_{2}-t_{1}=\pm\int _{{r_{1}}}^{{r_{2}}}\frac{dr}{\sqrt{\frac{2}{m}\big(E-g(r)-\frac{M^{2}}{2mr^{2}}\big)}}$

(5.20)

Chcąc znależć postać $\varphi(t)$ zauważmy, że ze związku $\dot{\varphi}r^{2}=M$ wynika, że $\dot{\varphi}$ jest ustalonego znaku a więc $\varphi$ jest monotoniczną funkcją $t_{1}$ i ma funkcję odwrotną $t(\varphi).$ Wobec tego $r(\varphi)=r\big(t(\varphi)\big)$ z zatem