Zagadnienia
1. Stochastyczne modele ekspresji genów
1.1. Krótki wstęp biologiczny
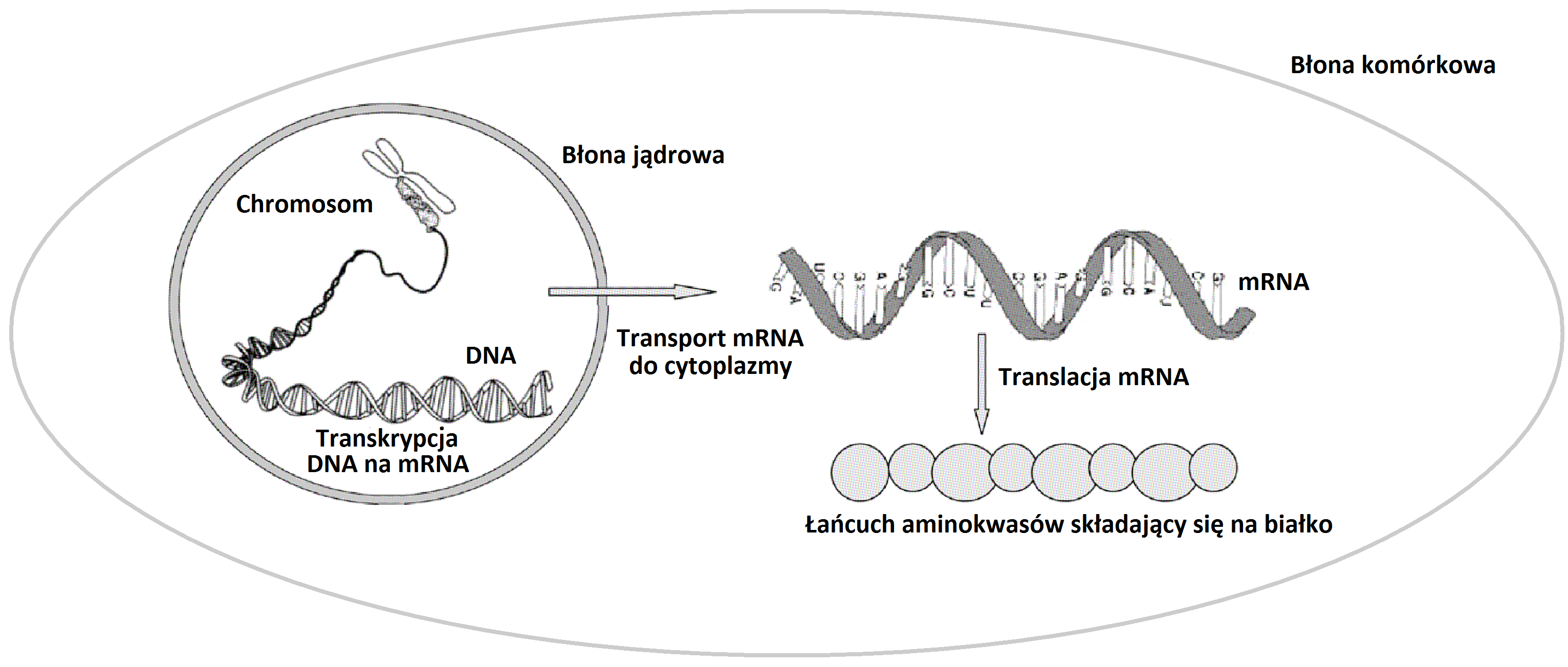
Jednym z podstawowych procesów biochemicznych zachodzących w komórkach żywych organizmów jest produkcja różnych białek. Jest to bardzo skomplikowany wieloetapowy proces. Każda cząsteczka białka składa się z połączonych w liniowy sposób odpowiednich aminokwasów. Opiszemy teraz w niezwykle uproszczony sposób jak dochodzi do połączenia aminokwasów w cząsteczkę białka (por. Rys. 1.1). Informacja genetyczna
umieszczona jest na nici kwasu DNA o strukturze podwójnej helisy. Wzdłuż nici DNA rozłożone są komplementarne zasady,
odpowiednio ATCG. Kod genetyczny jest kodem trójkowym, trzy następujące po sobie zasady kodują odpowiedni aminokwas.
Zauważmy, że mamy ![]() możliwości a tylko 23 aminokwasy, a więc mamy pewną nadmiarowość.
W procesie transkrypcji tworzona jest cząsteczka mRNA z komplementarnym ciągiem zasad, która zawiera plan na utworzenie białka. W komórkach eukariotycznych musi się ona wydostać z jądra komórkowego
do otaczającej go cytoplazmy, gdzie przyłącza się do niej rybosom.
W procesie translacji rybosom odczytując genetyczny kod trójkowy porusza się wzdłuż cząsteczki mRNA
i przyłącza po kolei odpowiednie cząsteczki aminokwasu tworzące łańcuch białkowy.
Wszystkie procesy składające się na produkcję białka nazwane są łącznie ekspresją białka.
możliwości a tylko 23 aminokwasy, a więc mamy pewną nadmiarowość.
W procesie transkrypcji tworzona jest cząsteczka mRNA z komplementarnym ciągiem zasad, która zawiera plan na utworzenie białka. W komórkach eukariotycznych musi się ona wydostać z jądra komórkowego
do otaczającej go cytoplazmy, gdzie przyłącza się do niej rybosom.
W procesie translacji rybosom odczytując genetyczny kod trójkowy porusza się wzdłuż cząsteczki mRNA
i przyłącza po kolei odpowiednie cząsteczki aminokwasu tworzące łańcuch białkowy.
Wszystkie procesy składające się na produkcję białka nazwane są łącznie ekspresją białka.
Uzyskane białko może pełnić bardzo różne funkcje: budulcowe, transportowe, regulatorowe. Regulacja białkowa może polegać na wzmacnianiu (aktywacji) lub osłabianiu (represji) produkcji innych białek lub też samego siebie (autoregulacja). Ostatnio odkryto, że podobne funkcje regulacyjne mogą również pełnić cząsteczki RNA.
1.2. Matematyczny model ekspresji genu
1.2.1. Opis deterministyczny na poziomie makro
Stan komórki jest opisany przez zależne od czasu koncentracje mRNA ![]() i białka
i białka ![]() . Ewolucję czasowa stanu komórki opisujemy równaniami kinetyki chemicznej - układem równań różniczkowych zwyczajnych
. Ewolucję czasowa stanu komórki opisujemy równaniami kinetyki chemicznej - układem równań różniczkowych zwyczajnych
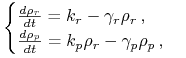 |
(1.1) |
gdzie ![]() i
i ![]() są odpowiednio intensywnościami tworzenia mRNA (transkrypcja) i białka (translacja),
natomiast
są odpowiednio intensywnościami tworzenia mRNA (transkrypcja) i białka (translacja),
natomiast ![]() i
i ![]() intensywnościami degradacji odpowiednio mRNA i białka.
W stanie stacjonarnym pochodne czasowe są równe zero, z (1) otrzymujemy układ równań algebraicznych,
którego rozwiązanie daje nam stacjonarne wartości koncentracji mRNA i białka:
intensywnościami degradacji odpowiednio mRNA i białka.
W stanie stacjonarnym pochodne czasowe są równe zero, z (1) otrzymujemy układ równań algebraicznych,
którego rozwiązanie daje nam stacjonarne wartości koncentracji mRNA i białka:
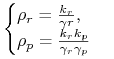 |
(1.2) |
1.2.2. Opis stochastyczny na poziomie mikro
W wielu komórkach, zwłaszcza prokariotycznych, liczba cząsteczek mRNA i białek może być niewielka
i w związku z tym mówienie o koncentracji traci sens. Mamy do czynienia ze skończonym układem czasami nawet kilku
cząsteczek danego białka i w związku z tym bardzo duża rolę odgrywają fluktuacje stochastyczne związane
z losowymi czasami zajścia odpowiednich reakcji biochemicznych. Na poziomie mikroskopowym stan komórki opisujemy
zależną od czasu liczbą cząsteczek mRNA ![]() i białka
i białka ![]() . Są to zmienne losowe. Stanem układu formalnie nazywamy
zależną od czasu funkcję rozkładu prawdopodobieństwa
. Są to zmienne losowe. Stanem układu formalnie nazywamy
zależną od czasu funkcję rozkładu prawdopodobieństwa ![]() tych zmiennych losowych czyli prawdopodobieństwo,
że w komórce będzie
tych zmiennych losowych czyli prawdopodobieństwo,
że w komórce będzie ![]() cząsteczek mRNA i
cząsteczek mRNA i ![]() cząsteczek białka. Ewolucja czasowa stanu układu jest więc procesem stochastycznym.
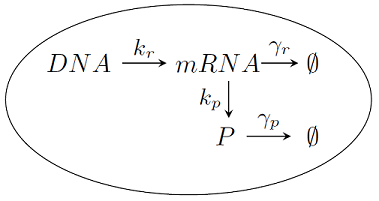
W naszej modelowej komórce zachodzą cztery typy reakcji biochemicznych (por. Rys 1.2): transkrypcja, translacja oraz degradacja mRNA i białka,
w wyniku których zmieniają się liczby odpowiednich cząsteczek.
cząsteczek białka. Ewolucja czasowa stanu układu jest więc procesem stochastycznym.
W naszej modelowej komórce zachodzą cztery typy reakcji biochemicznych (por. Rys 1.2): transkrypcja, translacja oraz degradacja mRNA i białka,
w wyniku których zmieniają się liczby odpowiednich cząsteczek.
Reakcje te opisywać będziemy przy pomocy procesu urodzin i śmierci (patrz Dodatek 1).
Przyjmujemy następujące prawdopodobieństwa zajścia reakcji w odcinku czasowym ![]() :
:
transkrypcji, czyli przejście
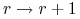 -
- 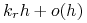
translacji, czyli przejście
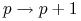 -
- 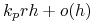
degradacji mRNA, czyli przejście
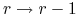 -
- 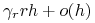
degradacji białka, czyli przejście
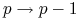 -
- 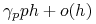 prawdopodobieństwo zajścia więcej niż jednej reakcji -
prawdopodobieństwo zajścia więcej niż jednej reakcji - 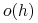
Naszym celem jest znalezienie wyrażenia na wariancje, ![]() , liczby cząsteczek białka w stanie stacjonarnym.
, liczby cząsteczek białka w stanie stacjonarnym.
Ćwiczenie 1.1
Skonstruuj nieskończony układ równań różniczkowych zwyczajnych dla ![]() .
.
Zastosuj procedurę z Dodatku!
Definiujemy funkcję tworzącą dla prawdopodobieństw ![]() ,
,
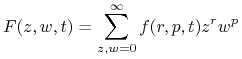 |
Ćwiczenie 1.2
Skonstruuj równanie różniczkowe cząstkowe dla ![]() wraz z warunkami brzegowymi i początkowymi.
wraz z warunkami brzegowymi i początkowymi.
Zastosuj procedurę z Dodatku 2.
Oznaczmy przez ![]() wartość oczekiwaną
wartość oczekiwaną ![]() . Mamy wtedy,
. Mamy wtedy,
Ćwiczenie 1.3
Zróżniczkuj powyższe równania ze względu na ![]() i otrzymaj układ równań różniczkowych zwyczajnych
dla następujących momentów:
i otrzymaj układ równań różniczkowych zwyczajnych
dla następujących momentów: ![]()
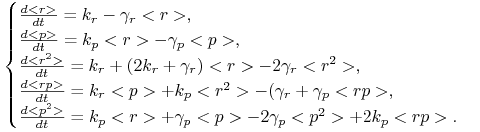 |
Zauważmy, że powyższy układ równań różniczkowych jest zamknięty, w równaniach dla danego momentu nie występują momenty wyższych rzędów - macierz układu równań jest trójkątna. Możemy więc po kolei rozwiązywać równania różniczkowe (porównaj (?)) i dostać wyrażenia na ewolucję czasową momentów. Zauważmy, że dwa pierwsze równania są takie same jak w układzie równań różniczkowych na koncentracje mRNA i białka w modelu deterministycznym (1.1).
Ćwiczenie 1.4
Znajdź wyrażenie na wariancję liczby cząsteczek białka w stanie stacjonarnym.
1.3. Proces Poissona
Proces Poissona to rodzina zmiennych losowych ![]() przyjmujących wartości całkowite
(na przykład liczba bakterii, cząstek lub ogólnie liczba zdarzeń) w czasie ciągłym.
przyjmujących wartości całkowite
(na przykład liczba bakterii, cząstek lub ogólnie liczba zdarzeń) w czasie ciągłym.
Założenia
Prawdopodobieństwo wystąpienia zmiany (urodzenia się jednej dodatkowej cząsteczki lub ogólnie wystąpienie pewnego zdarzenia) w odcinku czasowym
 wynosi
wynosi 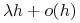 gdzie
gdzie 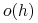 jest wielkością mniejszego rzędu niż
jest wielkością mniejszego rzędu niż 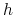 , to znaczy
, to znaczy 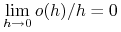 ;
;Prawdopodobieństwo wystąpienia więcej niż jednej zmiany w odcinku czasowym
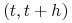 wynosi
wynosi 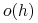 .
.
Zauważmy, że z powyższych założeń wynikają następujące własności:
Prawdopodobieństwo wystąpienia zdarzeń w rozłącznych odcinkach czasowych jest równe iloczynowi odpowiednich prawdopodobieństw (niezależność);
Prawdopodobieństwo wystąpienia zdarzenia nie zależy od czasu
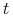 (jednorodność).
(jednorodność).
Oznaczmy przez ![]() prawdopodobieństwo, że nasz układ w chwili
prawdopodobieństwo, że nasz układ w chwili ![]() jest w stanie
jest w stanie ![]() , to znaczy zmienna losowa
, to znaczy zmienna losowa ![]() przyjmuje wartość
przyjmuje wartość ![]() (liczba cząstek w czasie
(liczba cząstek w czasie ![]() lub liczba zdarzeń do czasu
lub liczba zdarzeń do czasu ![]() wynosi
wynosi ![]() ).
).
Naszym celem jest znalezienie wzoru na ![]() .
.
Ćwiczenie 1.5
Skonstruuj równanie różniczkowe zwyczajne na ![]() .
.
Napisz wyrażenie na prawdopodobieństwo całkowite.
Wartość zmiennej losowej ![]() zależy od wartości
zależy od wartości ![]() i od tego co się zdarzyło w czasie
i od tego co się zdarzyło w czasie ![]() .
.
Możemy napisać wyrażenie na prawdopodobieństwo całkowite:
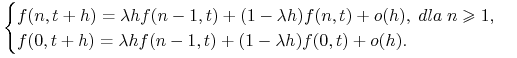 |
Przenosimy ![]() na lewą stronę, dzielimy przez
na lewą stronę, dzielimy przez ![]() , przechodzimy do granicy
, przechodzimy do granicy ![]() i otrzymujemy nieskończony układ równań różniczkowych zwyczajnych:
i otrzymujemy nieskończony układ równań różniczkowych zwyczajnych:
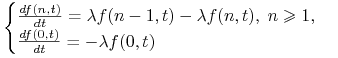 |
(1.3) |
z warunkiem początkowym ![]() .
.
Rozwiązujemy równanie różniczkowe na ![]() i otrzymujemy
i otrzymujemy
| (1.4) |
![]() jest prawdopodobieństwem, że czas oczekiwania na następne zdarzenie będzie większy od
jest prawdopodobieństwem, że czas oczekiwania na następne zdarzenie będzie większy od ![]() ,
czyli prawdopodobieństwem, że czas oczekiwania na następne zdarzenie będzie mniejszy niż
,
czyli prawdopodobieństwem, że czas oczekiwania na następne zdarzenie będzie mniejszy niż ![]() jest równy
jest równy ![]() . Jest to dystrybuanta rozkładu wykładniczego.
Oznacza to, że czas między zdarzeniami ma rozkład wykładniczy
. Jest to dystrybuanta rozkładu wykładniczego.
Oznacza to, że czas między zdarzeniami ma rozkład wykładniczy ![]() .
.
Rozwiązanie równania dla ![]() , czyli (1.4), wstawiamy do równania (1.3) dla
, czyli (1.4), wstawiamy do równania (1.3) dla ![]() ,
rozwiązanie wstawiamy do równania dla
,
rozwiązanie wstawiamy do równania dla ![]() . Iterując tą procedurę otrzymujemy wyrażenia dla
. Iterując tą procedurę otrzymujemy wyrażenia dla ![]() dla kolejnych
dla kolejnych ![]() .
.
Ćwiczenie 1.6
Sprawdzić, że
jest rozwiązaniem układu (1.3),
to znaczy, że ![]() jest zmienną losową Poissona z parametrem
jest zmienną losową Poissona z parametrem ![]() czyli z wartością oczekiwaną i wariancją równą
czyli z wartością oczekiwaną i wariancją równą ![]() .
.
1.4. Proces urodzin i śmierci
Tak jak i w procesie Poissona ![]() jest zmienną losową przyjmującą wartości całkowite.
Oprócz urodzin - zdarzeń podwyższających stan układu o 1,
dopuszczamy możliwość śmierci - zdarzeń obniżających stan układu o 1.
jest zmienną losową przyjmującą wartości całkowite.
Oprócz urodzin - zdarzeń podwyższających stan układu o 1,
dopuszczamy możliwość śmierci - zdarzeń obniżających stan układu o 1.
Zakładamy, że
Prawdopodobieństwo urodzenia się cząsteczki w odcinku czasowym
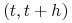 wynosi
wynosi 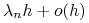
Prawdopodobieństwo śmierci cząsteczki w odcinku czasowym
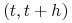 wynosi
wynosi 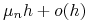
Przyjmiemy teraz, że ![]() i
i ![]() . Powtarzając procedurę zastosowaną dla procesu Poissona dostajemy następujący układ równań różniczkowych zwyczajnych:
. Powtarzając procedurę zastosowaną dla procesu Poissona dostajemy następujący układ równań różniczkowych zwyczajnych:
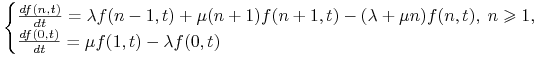 |
(1.5) |
Nie będziemy rozwiązywać tego układu równań różniczkowych. Interesować natomiast nas będzie stan stacjonarny,
![]() , który jest rozwiązaniem układu równań algebraicznych uzyskanych z (1.5) przy przyrównaniu do zera pochodnych czasowych.
Można wykazać, że
, który jest rozwiązaniem układu równań algebraicznych uzyskanych z (1.5) przy przyrównaniu do zera pochodnych czasowych.
Można wykazać, że ![]() , to znaczy
, to znaczy ![]() jest globalnie asymptotycznie stabilnym
punktem stacjonarnym układu (1.5).
jest globalnie asymptotycznie stabilnym
punktem stacjonarnym układu (1.5).
1.4.1. Błądzenie przypadkowe na kracie jednowymiarowej z czasem ciągłym
Jest to proces urodzin i śmierci, dla którego ![]() oraz
oraz ![]() .
Rozszerzamy jednocześnie zbiór wartości zmiennej losowej
.
Rozszerzamy jednocześnie zbiór wartości zmiennej losowej ![]() do zbioru liczb całkowitych.
do zbioru liczb całkowitych.
Układ (1.5) możemy wtedy przepisać jako
| (1.6) |
z warunkiem początkowym ![]() . Rozwiążemy powyższy układ przy pomocy funkcji tworzących. Definiujemy funkcję tworzącą dla dwustronnego ciągu prawdopodobieństw
. Rozwiążemy powyższy układ przy pomocy funkcji tworzących. Definiujemy funkcję tworzącą dla dwustronnego ciągu prawdopodobieństw ![]() ,
,
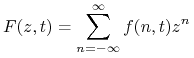 |
Różniczkując funkcję tworzącą ze względu na ![]() dostajemy momenty rozkładu prawdopodobieństwa
dostajemy momenty rozkładu prawdopodobieństwa ![]() .
W szczególności mamy:
.
W szczególności mamy:
gdzie ![]() oznacza wartość oczekiwaną
oznacza wartość oczekiwaną ![]() .
Różniczkując
.
Różniczkując ![]() względem czasu dostajemy
względem czasu dostajemy
warunek początkowy ![]() wynika bezpośrednio z definicji
wynika bezpośrednio z definicji ![]() i warunku początkowego dla
i warunku początkowego dla ![]() .
.
Rozwiązaniem powyższego równania różniczkowego jest
| (1.7) |
Ćwiczenie 1.7
Znajdź wartość oczekiwaną oraz wariancję ![]() .
.
Ćwiczenie 1.8
Znajdź ![]() .
.