Zagadnienia
2. Mechanika statystyczna
2.1. Dlaczego żelazo jest magnesem?
Jeżeli magnes wykonany z żelaza podgrzejemy powyżej 770 stopni Celsjusza, tak-zwanej temperatury Curie,
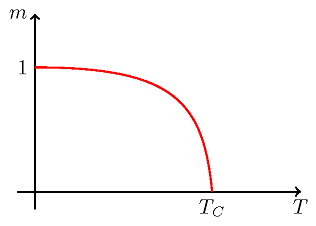
to straci on zdolności magnetyczne. Wykres namagnesowania jako funkcja temperatury ![]() jest podany na Rys. 2.1.
jest podany na Rys. 2.1.
Zjawisko te stara się wyjaśnić teoria ciała stałego, dział fizyki zajmujący się własnościami ciał makroskopowych. W bardzo dużym uproszczeniu przyjmujemy, że namagnesowanie sztabki żelaza jest sumą wektorową małych magnesów związanych z poszczególnymi atomami żelaza. Z jednej strony, siły oddziaływań pomiędzy magnesikami prowadzą do ich ułożenia wzdłuż jednego kierunku. Z drugiej strony, ruchy cieplne atomów zaburzają ten idealny porządek. Wynikiem tej rywalizacji pomiędzy czynnikiem energetycznym a czynnikiem losowym rosnącym w miarę wzrostu temperatury ciała są jego własności makroskopowe. Działem fizyki zajmującym się wyprowadzaniem własności makroskopowych ciał z mikroskopowych oddziaływań pomiędzy ich elementarnymi składnikami, atomami lub cząsteczkami, jest fizyka statystyczna.
2.2. Magnes matematyczny - Model Isinga
W modelu Isinga, oddziałujące obiekty - magnesiki - umieszczone są w węzłach kraty ![]() , gdzie
, gdzie ![]() jest zbiorem liczb całkowitych.
Kratę taką możemy uważać za regularny graf, w którym krawędzie łączą najbliższych sąsiadów, to znaczy każdy wierzchołek (węzeł) jest połączony
z wierzchołkiem z góry, z dołu, z prawa i z lewa. W każdym węźle
jest zbiorem liczb całkowitych.
Kratę taką możemy uważać za regularny graf, w którym krawędzie łączą najbliższych sąsiadów, to znaczy każdy wierzchołek (węzeł) jest połączony
z wierzchołkiem z góry, z dołu, z prawa i z lewa. W każdym węźle ![]() umieszczamy matematyczną reprezentację magnesiku,
umieszczamy matematyczną reprezentację magnesiku, ![]() ,
zmienną mogącą przyjmować dwie wartości: +1 (magnesik skierowany do góry) i -1 (magnesik skierowany do dołu). Zmienną
,
zmienną mogącą przyjmować dwie wartości: +1 (magnesik skierowany do góry) i -1 (magnesik skierowany do dołu). Zmienną ![]() nazywamy spinem
w wierzchołku
nazywamy spinem
w wierzchołku ![]() . Formalnie, zbiorem konfiguracji nieskończonego układu jest
. Formalnie, zbiorem konfiguracji nieskończonego układu jest ![]() , czyli zbiór wszystkich funkcji
przypisujących każdemu wierzchołkowi
, czyli zbiór wszystkich funkcji
przypisujących każdemu wierzchołkowi ![]() albo
albo ![]() . Dla danej konfiguracji
. Dla danej konfiguracji ![]() ,
, ![]() nazywamy konfiguracją w węźle
nazywamy konfiguracją w węźle ![]() . Niech
. Niech ![]() będzie skończonym podzbiorem węzłów naszej kraty.
będzie skończonym podzbiorem węzłów naszej kraty.
![]() jest zbiorem konfiguracji na
jest zbiorem konfiguracji na ![]() . Hamiltonian (funkcjonał energii) określa nam energię konfiguracji na
. Hamiltonian (funkcjonał energii) określa nam energię konfiguracji na ![]() .
.
| (2.1) |
Przyjmujemy, że oddziałują ze sobą spiny, które są najbliższymi sąsiadami.
| (2.2) |
gdzie ![]() jest parą najbliższych sąsiadów a
jest parą najbliższych sąsiadów a ![]() jest zewnętrznym polem magnetycznym.
jest zewnętrznym polem magnetycznym.
Hamiltonian w mechanice klasycznej oddziałujących cząstek jest sumą energii kinetycznej poszczególnych cząstek i energii potencjalnej oddziaływań między nimi (patrz wykład Wojtyńskiego). W powyższym wyrażeniu nie uwzględniamy energii potencjalnej.
Nasz układ spinowy podlega nieustannym ruchom cieplnym i w związku z tym jest układem stochastycznym.
Powinniśmy więc określić prawdopodobieństwa przebywania układu w każdym z mikroskopowych stanów
czyli elementów zbioru ![]() . Ponieważ zbiór zdarzeń elementarnych jest skończony,
zakładamy że wszystkie jego podzbiory są mierzalne i wobec tego do zadania miary prawdopodobieństwa
wystarczy określić prawdopodobieństwo każdego elementu
. Ponieważ zbiór zdarzeń elementarnych jest skończony,
zakładamy że wszystkie jego podzbiory są mierzalne i wobec tego do zadania miary prawdopodobieństwa
wystarczy określić prawdopodobieństwo każdego elementu ![]() .
Miara prawdopodobieństwa na
.
Miara prawdopodobieństwa na ![]() jest interpretowana jako stan równowagowy układu fizycznego oddziałujących spinów.
Mówi ona nam z jakimi prawdopodobieństwami (w stanie równowagi) układ znajduje się w poszczególnych stanach mikroskopowych.
Wszelkie makroskopowe wielkości fizyczne, takie jak energia (
jest interpretowana jako stan równowagowy układu fizycznego oddziałujących spinów.
Mówi ona nam z jakimi prawdopodobieństwami (w stanie równowagi) układ znajduje się w poszczególnych stanach mikroskopowych.
Wszelkie makroskopowe wielkości fizyczne, takie jak energia (![]() ) czy namagnesowanie układu, są więc zmiennymi losowymi na przestrzeni
) czy namagnesowanie układu, są więc zmiennymi losowymi na przestrzeni ![]() .
Interesować nas będą wartości oczekiwane tych zmiennych losowych. W szczególności definiujemy namagnesowanie układu,
.
Interesować nas będą wartości oczekiwane tych zmiennych losowych. W szczególności definiujemy namagnesowanie układu,
| (2.3) |
Wprowadzamy następujący rozkład prawdopodobieństwa,
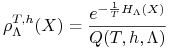 |
(2.4) |
gdzie ![]() jest temperaturą układu, miarą jego ruchów cieplnych a
jest temperaturą układu, miarą jego ruchów cieplnych a
| (2.5) |
jest czynnikiem normalizującym prawdopodobieństwo. W fizyce ![]() nazywane jest sumą statystyczną
natomiast
nazywane jest sumą statystyczną
natomiast ![]() wielkim rozkładem kanonicznym. Odłożymy do następnego podrozdziału
uzasadnienie wprowadzenia takiego a nie innego rozkładu prawdopodobieństwa.
wielkim rozkładem kanonicznym. Odłożymy do następnego podrozdziału
uzasadnienie wprowadzenia takiego a nie innego rozkładu prawdopodobieństwa.
Niezwykle ważną wielkością w fizyce jest energia swobodna, zwana także potencjałem termodynamicznym,
| (2.6) |
Wartości oczekiwane zmiennych losowych możemy dostać różniczkując potencjał. W szczególności łatwo zobaczyć, że
| (2.7) |
Ćwiczenie 2.1
Udowodnij powyższą równość.
Ćwiczenie 2.2
Udowodnij, że ![]()
2.2.1. Metoda konturów Peierlsa
Będziemy rozważać układy z plusowymi albo minusowymi warunkami brzegowymi w dwuwymiarowym modelu Isinga, ![]() ,
,
Zbiory konfiguracji ![]() i
i ![]() możemy utożsamiać z
możemy utożsamiać z ![]() .
Wprowadzamy Hamiltonian z plusowymi warunkami brzegowymi i z zewnętrznym polem magnetycznym
.
Wprowadzamy Hamiltonian z plusowymi warunkami brzegowymi i z zewnętrznym polem magnetycznym ![]() ,
,
| (2.8) |
Wtedy odpowiedni wielki kanoniczny rozkład prawdopodobieństwa ma następującą postać,
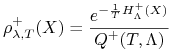 |
(2.9) |
Przyjmijmy dla uproszczenia, że ![]() jest kwadratem o boku
jest kwadratem o boku ![]() i środku w
i środku w ![]() ,
,
![]() Jest intuicyjnie jasne, że prawdopodobieństwo tego, że
Jest intuicyjnie jasne, że prawdopodobieństwo tego, że ![]() w powyższym rozkładzie jest większe od
w powyższym rozkładzie jest większe od ![]() ,
plusowe warunki brzegowe łamią symetrię Hamiltonianu - faworyzują spiny skierowane do góry.
Wiemy, że bez warunków brzegowych prawdopodobieństwo powyższe wynosi
,
plusowe warunki brzegowe łamią symetrię Hamiltonianu - faworyzują spiny skierowane do góry.
Wiemy, że bez warunków brzegowych prawdopodobieństwo powyższe wynosi ![]() .
Wydawałoby się, że jeżeli będziemy odsuwać warunki brzegowe do nieskończoności,
czyli przejdziemy do granicy termodynamicznej
.
Wydawałoby się, że jeżeli będziemy odsuwać warunki brzegowe do nieskończoności,
czyli przejdziemy do granicy termodynamicznej ![]() ,
to znaczy
,
to znaczy ![]() , ich wpływ będzie zanikał. Rozważmy graniczną miarę, nazywaną stanem albo miara Gibbsa,
, ich wpływ będzie zanikał. Rozważmy graniczną miarę, nazywaną stanem albo miara Gibbsa,
gdzie poprzez zbieżność rozumiemy słabą zbieżność z gwiazdką miar na ![]() z odpowiednio określonym
z odpowiednio określonym ![]() -ciałem
-ciałem ![]() , patrz dalej.
Zanikający wpływ warunków brzegowych oznaczałby, że
, patrz dalej.
Zanikający wpływ warunków brzegowych oznaczałby, że ![]() czyli wartość średnia namagnesowania jest równa
czyli wartość średnia namagnesowania jest równa ![]() ,
,
![]() . Poniżej pokażemy, że dla odpowiednio małych temperatur średnie namagnesowanie jest dowolnie bliskie
. Poniżej pokażemy, że dla odpowiednio małych temperatur średnie namagnesowanie jest dowolnie bliskie ![]() .
Udowodnimy następujące fundamentalne twierdzenie
.
Udowodnimy następujące fundamentalne twierdzenie
Twierdzenie 2.1
![]() gdzie
gdzie ![]()
Oznacza to, że choć brzegu już nie ma, pozostał jego ślad. Hamiltonian w granicy termodynamicznej dla ![]() jest niezmienniczy ze względu na odwrócenie spinów, natomiast stany Gibbsa nie są,
jest niezmienniczy ze względu na odwrócenie spinów, natomiast stany Gibbsa nie są, ![]() .
Spontaniczne złamanie symetrii - Twierdzenie 2.1 - zachodzi w granicy termodynamicznej dla nieskończonego układu.
Udowodnimy je korzystając z aparatu dyskretnego rachunku prawdopodobieństwa dla skończonych stanów Gibbsa,
z nierówności jednostajnych ze względu na wielkość układu (
.
Spontaniczne złamanie symetrii - Twierdzenie 2.1 - zachodzi w granicy termodynamicznej dla nieskończonego układu.
Udowodnimy je korzystając z aparatu dyskretnego rachunku prawdopodobieństwa dla skończonych stanów Gibbsa,
z nierówności jednostajnych ze względu na wielkość układu (![]() ).
Teza Twierdzenia 2.1 wynika bezpośrednio z następującego twierdzenia,
).
Teza Twierdzenia 2.1 wynika bezpośrednio z następującego twierdzenia,
Twierdzenie 2.2
![]() gdzie
gdzie ![]() jednostajnie ze względu na
jednostajnie ze względu na ![]() .
.
Wprowadzimy teraz pojęcie konturu konfiguracji.
Dla każdej pary sąsiadów ![]() , niech
, niech ![]() będzie odcinkiem w
będzie odcinkiem w ![]() o długości
o długości ![]() ,
prostopadłym do odcinka łączącego
,
prostopadłym do odcinka łączącego ![]() z
z ![]() i takim że oba odcinki przecinają się w połowie.
Konturem konfiguracji
i takim że oba odcinki przecinają się w połowie.
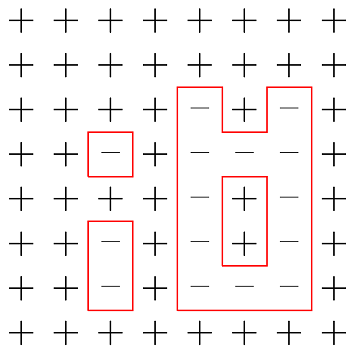
Konturem konfiguracji ![]() nazywamy każdy maksymalny spójny zbiór odcinków oddzielających
plusy od minusów (dwa kontury stykające się w jednym punkcie uważamy za rozłączne), patrz Rys. 2.2.
nazywamy każdy maksymalny spójny zbiór odcinków oddzielających
plusy od minusów (dwa kontury stykające się w jednym punkcie uważamy za rozłączne), patrz Rys. 2.2.
Formalnie,
Konturem ![]() jest każdy maksymalny spójny podzbiór
jest każdy maksymalny spójny podzbiór ![]() . Zbiór wszystkich konturów konfiguracji
. Zbiór wszystkich konturów konfiguracji ![]() oznaczamy przez
oznaczamy przez ![]() .
Niech
.
Niech ![]() .
Wprowadzamy operator wymazywania konturu,
.
Wprowadzamy operator wymazywania konturu,
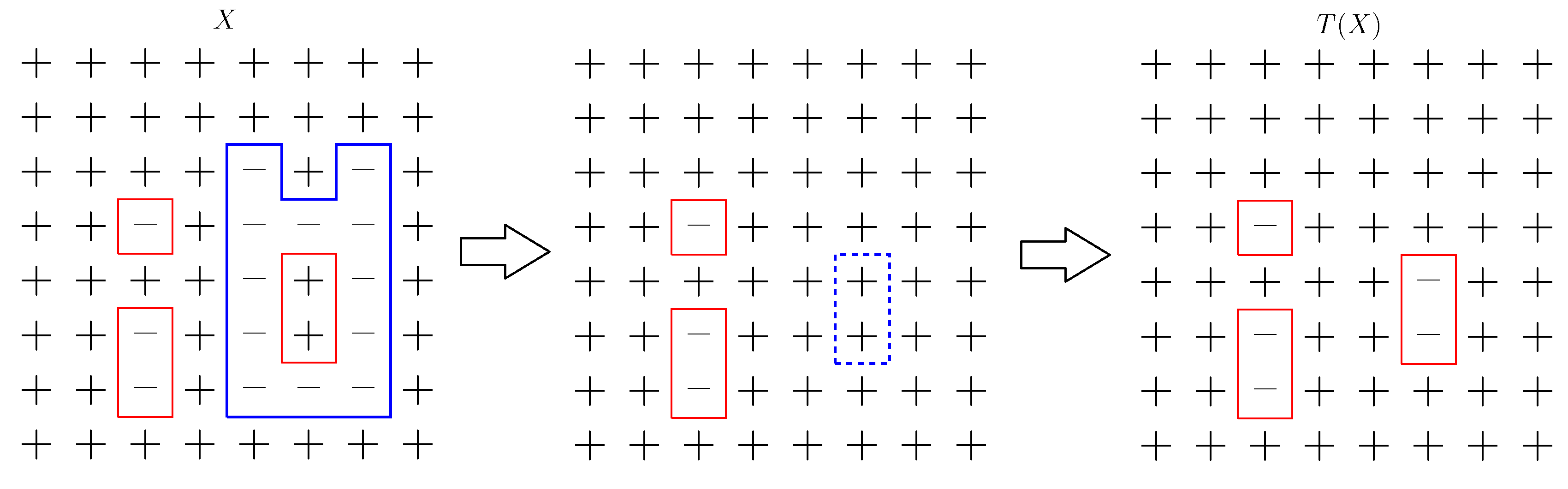
Definiujemy ![]() w następujący sposób. Kontur
w następujący sposób. Kontur ![]() dzieli
dzieli ![]() na dwie części: wewnątrz konturu i na zewnątrz.
Aby dostać
na dwie części: wewnątrz konturu i na zewnątrz.
Aby dostać ![]() , zmieniamy w konfiguracji
, zmieniamy w konfiguracji ![]() znaki w wierzchołkach
znaki w wierzchołkach ![]() wewnątrz konturu
wewnątrz konturu ![]() ,
następnie czynimy to samo dla wszystkich konturów bezpośrednio wewnątrz
,
następnie czynimy to samo dla wszystkich konturów bezpośrednio wewnątrz ![]() i kolejno dla konturów wewnątrz
poprzednich konturów, patrz Rys. 2.3. Zauważmy, że operator T jest wzajemnie jednoznaczny.
i kolejno dla konturów wewnątrz
poprzednich konturów, patrz Rys. 2.3. Zauważmy, że operator T jest wzajemnie jednoznaczny.
Dowód Twierdzenia 2
| (2.10) |
gdzie sumowanie jest po konturach otaczających ![]() a
a ![]() jest długością konturu czyli liczbą tworzących go odcinków jednostkowych.
Łatwo zauważyć, że liczbę konturów (łamanych) o długości
jest długością konturu czyli liczbą tworzących go odcinków jednostkowych.
Łatwo zauważyć, że liczbę konturów (łamanych) o długości ![]() można oszacować z góry przez
można oszacować z góry przez ![]() .
Do oszacowania drugiego czynnika w 2.10 użyjemy operatora wymazywania konturów.
.
Do oszacowania drugiego czynnika w 2.10 użyjemy operatora wymazywania konturów.
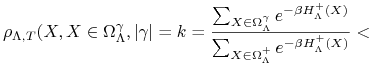 |
(2.11) |
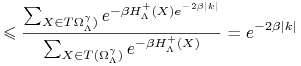 |
Ostatecznie mamy
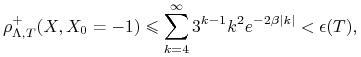 |
(2.12) |
gdzie ![]() jeśli
jeśli ![]() i otrzymujemy tezę Twierdzenia 2.
i otrzymujemy tezę Twierdzenia 2.
W analogiczny sposób dla minusowych warunków brzegowych otrzymujemy
i ![]() Otrzymaliśmy więc dwa stany Gibbsa dla tego samego oddziaływania i takiej samej temperatury.
Układ może więc znajdować się w dwóch różnych fazach, które mogą współistnieć tak jak lód i woda w temperaturze 0 stopni Celsjusza.
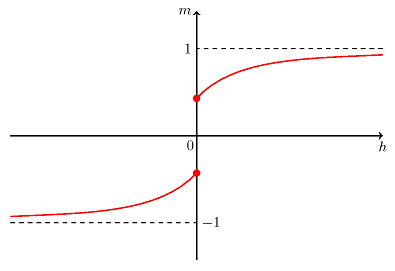
Mówimy, że mamy do czynienia z przejściem fazowym pierwszego rodzaju. Jest to przejście typu nieciągłego - gęstość wody zmienia się
w sposób nieciągły przy przejściu z fazy stałej do ciekłej. W modelu ferromagnetycznym Isinga namagnesowanie zmienia się w sposób nieciągły
przy przejściu zewnętrznego pola magnetycznego przez zero, patrz Rys. 2.4.
Otrzymaliśmy więc dwa stany Gibbsa dla tego samego oddziaływania i takiej samej temperatury.
Układ może więc znajdować się w dwóch różnych fazach, które mogą współistnieć tak jak lód i woda w temperaturze 0 stopni Celsjusza.
Mówimy, że mamy do czynienia z przejściem fazowym pierwszego rodzaju. Jest to przejście typu nieciągłego - gęstość wody zmienia się
w sposób nieciągły przy przejściu z fazy stałej do ciekłej. W modelu ferromagnetycznym Isinga namagnesowanie zmienia się w sposób nieciągły
przy przejściu zewnętrznego pola magnetycznego przez zero, patrz Rys. 2.4.
Natomiast przy obniżaniu temperatury, w temperaturze Curie mamy do czynienia z przejściem fazowym drugiego rodzaju. Jest to przejście fazowe typu ciągłego - namagnesowanie w sposób ciągły wzrasta od zera przy podwyższaniu temperatury powyżej punktu Curie, patrz Rys. 2.1.
2.2.2. Jednowymiarowy model Isinga
2.3. Klasyczne gazy sieciowe
W rozdziale tym uogólnimy klasyczny model Isinga na przypadek więcej niż dwóch możliwych stanów, w których może znajdować się każdy
wierzchołek sieci, na oddziaływania o większym zasięgu i niekoniecznie dwucząstkowe. Nasze modele będziemy interpretować
w języku gazów sieciowych. W modelu gazu sieciowego w każdym wierzchołku sieci ![]() znajduje się jedna cząstka o określonym typie.
Zakładamy skończona liczbę typów. Zbiorem konfiguracji nieskończonego układu oddziałujących cząstek jest więc
znajduje się jedna cząstka o określonym typie.
Zakładamy skończona liczbę typów. Zbiorem konfiguracji nieskończonego układu oddziałujących cząstek jest więc
Przez potencjał ![]() oddziaływania cząstek rozumiemy nieskończoną rodzinę funkcji indeksowaną skończonymi podzbiorami
oddziaływania cząstek rozumiemy nieskończoną rodzinę funkcji indeksowaną skończonymi podzbiorami ![]()
Definicja 2.1
![]() jest oddziaływaniem o skończonym zasięgu
jest oddziaływaniem o skończonym zasięgu ![]() , jeśli
, jeśli ![]() dla
dla ![]() .
.
Definicja 2.2
![]() jest oddziaływaniem translacyjnie niezmienniczym, jeśli
jest oddziaływaniem translacyjnie niezmienniczym, jeśli ![]() dla każdego
dla każdego ![]() , gdzie
, gdzie ![]() jest operatorem przesunięcia o wektor
jest operatorem przesunięcia o wektor ![]() czyli
czyli ![]() .
.
Widzimy więc, że model Isinga zadany jest przez potencjał dwucząstkowy o zasięgu ![]() .
.
Definicja 2.3
Hamiltonianem w skończonej objętości ![]() jest funkcjonał
jest funkcjonał ![]() .
.
Definicja 2.4
Konfiguracja ![]() jest lokalnym zaburzeniem konfiguracji
jest lokalnym zaburzeniem konfiguracji ![]() , ozn.
, ozn. ![]() , jeśli
, jeśli ![]() .
.
Podstawowym pojęciem w mechanice statystycznej oddziałujących cząstek jest stan podstawowy. Intuicyjnie są to konfiguracje o najmniejszej energii. Energia nieskończonej konfiguracji zazwyczaj bywa nieskończona. Tak więc intuicyjna definicja nie ma sensu. Zamiast energii rozważmy w takim razie gęstość energii
Definicja 2.5
![]() jest gęstością energii konfiguracji
jest gęstością energii konfiguracji ![]() .
.
Chcielibyśmy zdefiniować konfiguracje stanu podstawowego jako te, które minimalizują gęstość energii.
Uwolniliśmy się od nieskończonych energii ale mamy inny kłopot. Jeśli ![]() byłoby konfiguracja stanu podstawowego w myśl powyższej definicji,
to każde jej lokalne zaburzenie też miałoby minimalną gęstość energii, więc też byłoby konfiguracją stanu podstawowego,
co jest oczywistym absurdem. Musimy być bardziej subtelni. Wprowadzimy pojęcie Hamiltonianu względnego.
byłoby konfiguracja stanu podstawowego w myśl powyższej definicji,
to każde jej lokalne zaburzenie też miałoby minimalną gęstość energii, więc też byłoby konfiguracją stanu podstawowego,
co jest oczywistym absurdem. Musimy być bardziej subtelni. Wprowadzimy pojęcie Hamiltonianu względnego.
Definicja 2.6
Dla lokalnego wzbudzenia ![]() , Hamiltonianem względnym jest
, Hamiltonianem względnym jest ![]() .
.
Definicja 2.7
![]() jest konfiguracją stanu podstawowego potencjału
jest konfiguracją stanu podstawowego potencjału ![]() ,
jeśli dla dowolnego lokalnego wzbudzenia,
,
jeśli dla dowolnego lokalnego wzbudzenia, ![]() ,
, ![]() .
.
Powyższa definicja ma charakter lokalny. Konfiguracja stanu podstawowego jest taką konfiguracją, której nie można lokalnie zaburzyć tak aby zmniejszyć wartość Hamiltonianu względnego. Zastanowimy się teraz w jakim sensie konfiguracje stanu podstawowego posiadają własność globalnego minimum energii.
Twierdzenie 2.3
Jeśli ![]() jest konfiguracją stanu podstawowego, to
jest konfiguracją stanu podstawowego, to ![]() minimalizuje gęstość energii,
to znaczy
minimalizuje gęstość energii,
to znaczy ![]() dla każdego
dla każdego ![]()
Ćwiczenie 2.3
Udowodnij powyższe twierdzenie.
Odwrotna implikacja nie jest oczywiście prawdziwa. Twierdzenie odwrotne zachodzi natomiast jeżeli będziemy rozważać tylko konfiguracje okresowe.
Definicja 2.8
![]() jest konfiguracją okresową jeśli istnieją trzy liczby naturalne
jest konfiguracją okresową jeśli istnieją trzy liczby naturalne ![]() ,
takie że
,
takie że ![]() , gdzie
, gdzie ![]()
Mamy następującą postać twierdzenia odwrotnego.
Twierdzenie 2.4
![]() jest okresową konfiguracja stanu podstawowego,
jeśli
jest okresową konfiguracja stanu podstawowego,
jeśli ![]() dla każdej okresowej konfiguracji
dla każdej okresowej konfiguracji ![]() .
.
Ćwiczenie 2.4
Znajdź wszystkie konfiguracje stanu podstawowego dwuwymiarowego ferromagnetycznego modelu Isinga.
Twierdzenie 2.5
Dla każdego translacyjnie niezmienniczego potencjału skończenie zasięgowego, zbiór konfiguracji stanu podstawowego jest niepusty.
Ćwiczenie 2.5
Udowodnij powyższe twierdzenie.
Skorzystaj z tego, że ![]() jest zbiorem zwartym w odpowiedniej topologii, patrz Dodatek X
jest zbiorem zwartym w odpowiedniej topologii, patrz Dodatek X
2.4. Kwazikryształy
Rozpoczniemy od fundamentalnego pytania: czy każdy skończenie zasięgowy translacyjnie niezmienniczy potencjał posiada co najmniej jedną okresową konfigurację stanu podstawowego?
Poniżej zamieszczamy krótki szkic rozumowania zamieszczonego w książce P.W. Andersona ….. i mającego odpowiadać twierdząco na powyższe pytanie.
Ćwiczenie 2.6
Znajdź błąd w powyższym rozumowaniu.
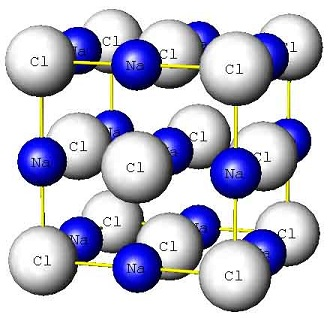
W tym samym 1984 roku odkryto kwazikryształy, których atomy rozmieszczone są w przestrzeni w sposób nieokresowy []. Był to pierwszy eksperymentalny kontrprzykład do ogólnie przyjętej hipotezy, że ciało stałe przy odpowiednio niskich temperaturach zawsze powinno występować w formie krystalicznej czyli przestrzennie okresowej. Typowym przykładem są kryształki soli kamiennej NaCL, w których atomy sodu i chloru tworzą okresową strukturę przedstawioną na Rys. 2.5.
Ćwiczenie 2.7
Udowodnij, że każdy jednowymiarowy translacyjnie-niezmienniczy skończenie-zasięgowy potencjał gazu sieciowego posiada co najmniej jedną okresową konfigurację stanu podstawowego.
Każda jednowymiarowa konfiguracja może być przedstawiona jako nieskończona droga na pewnym grafie
2.5. Nieokresowe mozaiki - krótka historia rekordu świata
W rozdziale tym będziemy rozważać pokrycia płaszczyzny wielobokami nazywanymi przez nas kafelkami lub dachówkami. Wybieramy skończoną liczbę kafelków, nazywamy je prototypami. Mamy do dyspozycji nieskończoną liczbę kopii każdego prototypu. Staramy się pokryć nimi nieskończoną płaszczyznę tak aby każdy punkt płaszczyzny został pokryty i żeby kafelki nie miały części wspólnych (z wyjątkiem brzegów).
W 1900 roku David Hilbert zaprezentował 23 fundamentalne problemy matematyczne. Druga cześć 18-tego problemu zawiera w istocie następujące (nadal pozostawione bez odpowiedzi) pytanie: Czy istnieje wielobok pokrywający nieskończoną płaszczyznę tylko w sposób nieokresowy?
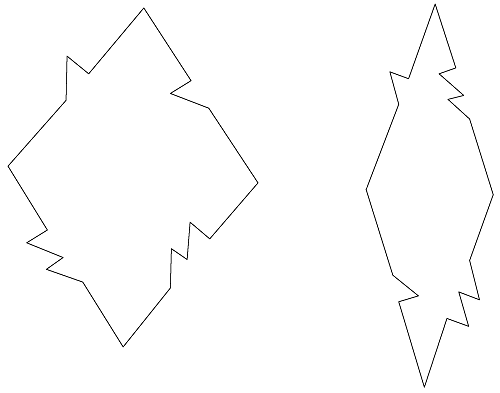
W 1974 roku, na długo przed odkryciem kwazikryształów, Roger Penrose, fizyk matematyczny z Oxfordu, skonstruował (albo odkrył jak kto woli) dwie dachówki, zwane latawcem i grotem, którymi można pokryć płaszczyznę tylko w sposób nieokresowy, Rys. 2.6 (patrz artykuł w delcie i Scientific American).
W dalszej części tego rozdziału będziemy zajmować się dachówkami kwadratowymi z wcięciami i wypustkami na bokach.
Wcięcia i wypustki możemy reprezentować odpowiednimi kolorami boków. Dwa sąsiednie kwadraty pasują do siebie gdy wypustki jednego pasują
do wcięć drugiego albo alternatywnie kolory odpowiednich boków są takie same. Dachówki takie nazywane są dominami albo dachówkami Wanga.
Jeżeli można nimi pokryć płaszczyznę, to ich środki tworzą regularny graf ![]() . Nieskończone pokrycie płaszczyzny dachówkami jest nazywane
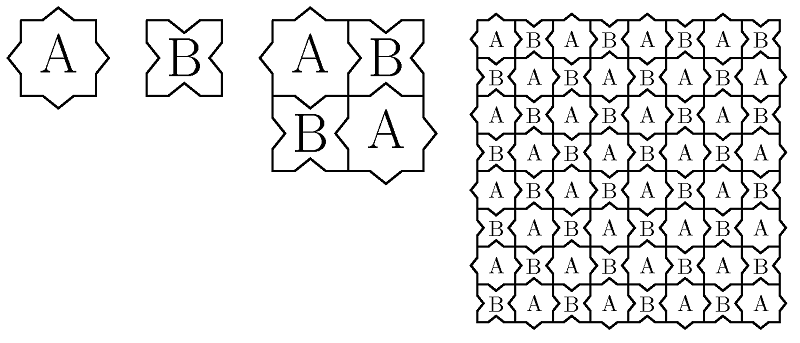
mozaiką albo po prostu pokryciem. Jest oczywiste, że kwadratowe kafelki bez żadnych kolorowań mogą pokryć płaszczyznę i to na wiele okresowych
i nieokresowych sposobów; jedno z takich pokryć jest bardzo dobrze znane każdemu kafelkarzowi. Na Rys. 2.7 zaprezentowano dwa kafelki i jedyne pokrycie płaszczyzny.
. Nieskończone pokrycie płaszczyzny dachówkami jest nazywane
mozaiką albo po prostu pokryciem. Jest oczywiste, że kwadratowe kafelki bez żadnych kolorowań mogą pokryć płaszczyznę i to na wiele okresowych
i nieokresowych sposobów; jedno z takich pokryć jest bardzo dobrze znane każdemu kafelkarzowi. Na Rys. 2.7 zaprezentowano dwa kafelki i jedyne pokrycie płaszczyzny.
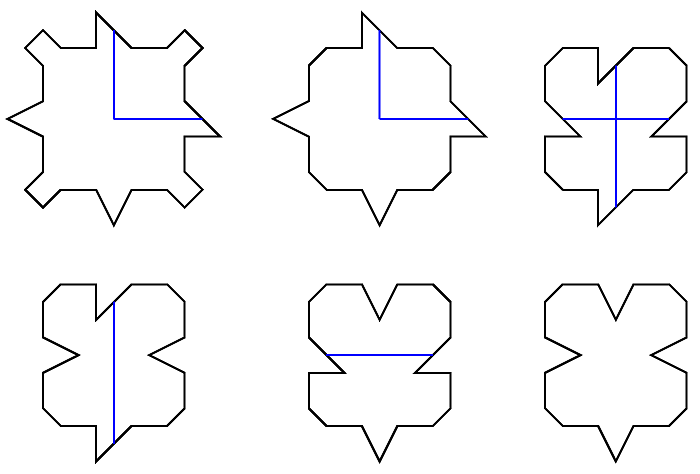
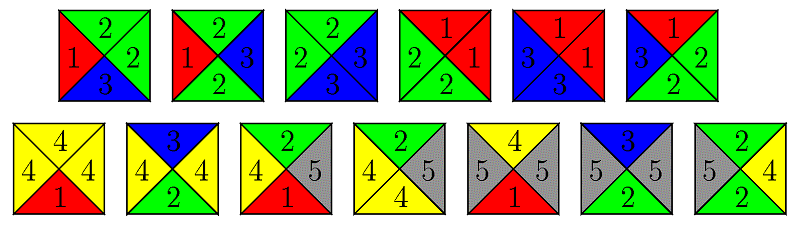
W 1961 roku Hao Wang postawił hipotezę, że każdy skończony zestaw płytek domina pokrywający płaszczyznę może pokryć ją także w sposób okresowy. Hipoteza ta miała związek z problem rozstrzygalności - czy istnieje uniwersalny program komputerowy (maszyna Turinga), który w skończonej liczbie kroków dostarczyłby odpowiedzi na pytanie czy dany zestaw domin może pokryć płaszczyznę. Jeżeli powyższa hipoteza byłaby prawdziwa, to próbując stopniowo pokrywać coraz większe obszary płaszczyzny odkrylibyśmy w skończonej liczbie kroków układ domin, który moglibyśmy powtarzać i skonstruować w ten sposób pokrycie okresowe. Pierwszy kontrprzykład pojawił się w 1996 roku i jest autorstwa Roberta Bergera []. Zaprojektował on 20426 kafelków pokrywających płaszczyznę tylko w sposób nieokresowy. W 1971 roku Raphael Robinson obniżył liczbę dachówek o tej własności do 56 []. Na Rys. 2.8 zaprezentowanych jest 6 dachówek Robinsona, pozostałe można z nich otrzymać przy pomocy obrotów i odbić.
Na Rys. 2.9 pokazana jest struktura nieokresowej mozaiki Robinsona.
W 1977 Robert Ammann ustanowił nowy rekord świata minimalnej liczby kafelków pokrywających płaszczyznę tylko w sposób nieokresowy. Następnym rekordzistą został w 1996 roku Jarrko Kari z 14 kafelkami) []. Obecny rekord 13 kafelków, też z 1996 roku, należy do Karela Culika II [], Rys. 2.10.
Zapraszam do pobicia rekordu świata.
2.6. Mikroskopowy model kwazikryształu
Zaprezentujemy teraz translacyjnie niezmienniczy skończenie zasięgowy potencjał gazu sieciowego nieposiadający żadnej okresowej
konfiguracji stanu podstawowego. Nasza konstrukcja opiera się na nieokresowych mozaikach. Przykładowo użyjemy dachówek Ammanna.
Każdą dachówkę na Rys. X traktujemy jako rodzaj cząstki. Zbiorem konfiguracji gazu sieciowego jest więc ![]() .
Energia oddziaływania dwóch sąsiednich cząstek jest równa
.
Energia oddziaływania dwóch sąsiednich cząstek jest równa ![]() jeśli odpowiadające im dachówki pasują do siebie, w przeciwnym przypadku energia
jest dodatnia, powiedzmy równa
jeśli odpowiadające im dachówki pasują do siebie, w przeciwnym przypadku energia
jest dodatnia, powiedzmy równa ![]() . Nieskończone mozaiki odpowiadają więc konfiguracjom stanu podstawowego o gęstości energii
. Nieskończone mozaiki odpowiadają więc konfiguracjom stanu podstawowego o gęstości energii ![]() - wszystkie dachówki
pasują do siebie. Brak okresowych mozaik pociąga za sobą nieistnienie okresowych stanów podstawowych w naszym modelu.
- wszystkie dachówki
pasują do siebie. Brak okresowych mozaik pociąga za sobą nieistnienie okresowych stanów podstawowych w naszym modelu.
Fundamentalnym pytaniem jest czy nieokresowa struktura obecna w konfiguracjach stanu podstawowego, czyli w zerowej temperaturze, przetrwa w dodatniej temperaturze. Innymi słowy czy struktura nieokresowa jest odporna na dowolnie małe cieplne fluktuacje.
Czy istnieje klasyczny model gazu sieciowego z translacyjnie niezmienniczym skończenie zasięgowym potencjałem bez okresowych konfiguracji stanów podstawowych i z nieokresowym stanem Gibbsa?
Rozważmy model gazu sieciowego odpowiadający dachówkom Ammanna. Niech Y będzie jedną z nieokresowych konfiguracji stanu podstawowego,
![]() stanem Gibbsa w skończonym obszarze
stanem Gibbsa w skończonym obszarze ![]() z warunkami brzegowymi
z warunkami brzegowymi ![]() poza
poza ![]() a
a ![]() stanem Gibbsa w granicy termodynamicznej.
stanem Gibbsa w granicy termodynamicznej.
Czy dla każdego ![]() , istnieje temperatura
, istnieje temperatura ![]() , taka że jeśli
, taka że jeśli ![]() , to
, to ![]() ?
?
Odpowiedź twierdząca na powyższe pytanie pociąga za sobą nieokresowość ![]() .
Symulacje komputerowe przemawiające za taką sytuacją można zmaleźć w []. Jednocześnie należy wspomnieć o hipotezie
mówiącej o nieistnieniu nieokresowych stanów Gibbsa w modelach dwuwymiarowych. Z każdego dwuwymiarowego modelu można
stworzyć w łatwy sposób model trójwymiarowy. Do oddziaływań w
.
Symulacje komputerowe przemawiające za taką sytuacją można zmaleźć w []. Jednocześnie należy wspomnieć o hipotezie
mówiącej o nieistnieniu nieokresowych stanów Gibbsa w modelach dwuwymiarowych. Z każdego dwuwymiarowego modelu można
stworzyć w łatwy sposób model trójwymiarowy. Do oddziaływań w ![]() dodajemy oddziaływania najbliższych sąsiadów wzdłuż
kierunku prostopadłego do
dodajemy oddziaływania najbliższych sąsiadów wzdłuż
kierunku prostopadłego do ![]() - energia oddziaływania dwóch takich samych cząstek będących najbliższymi sąsiadami
jest równa zero, energia każdej pary składającej się z różnych cząstek jest dodatnia, powiedzmy
- energia oddziaływania dwóch takich samych cząstek będących najbliższymi sąsiadami
jest równa zero, energia każdej pary składającej się z różnych cząstek jest dodatnia, powiedzmy ![]() .
Widzimy, że dwuwymiarowe konfiguracje stanu podstawowego propagują się wzdłuż kierunku prostopadłego do
.
Widzimy, że dwuwymiarowe konfiguracje stanu podstawowego propagują się wzdłuż kierunku prostopadłego do ![]() .
.
Modele gazów sieciowych odpowiadające dachówkom Robinsona badane były w [].
2.6.1. Dodatek 2
Zbiór wszystkich konfiguracji gazu sieciowego z ![]() różnymi typami cząstek,
różnymi typami cząstek,
jest zbiorem nieprzeliczalnym.
Aby rozważać miary na tym zbiorze musimy wprowadzić ![]() -ciało zbiorów mierzalnych. Na początek zdefiniujemy zbiory otwarte
czyli wprowadzimy na
-ciało zbiorów mierzalnych. Na początek zdefiniujemy zbiory otwarte
czyli wprowadzimy na ![]() topologię. Rozpoczniemy od tego, że na skończonym zbiorze
topologię. Rozpoczniemy od tego, że na skończonym zbiorze ![]() wprowadzimy topologię dyskretną
czyli każdy podzbiór
wprowadzimy topologię dyskretną
czyli każdy podzbiór ![]() jest jednocześnie otwarty i domknięty. Na
jest jednocześnie otwarty i domknięty. Na
wprowadzamy topologię produktową
czyli najmniejsza topologię, w której projekcje ![]() ,
, ![]() ,
, ![]() są funkcjami ciągłymi. Zbiór skończony z topologią dyskretną jest oczywiście zwarty. Z Twierdzenia Tichonowa wynika, że
są funkcjami ciągłymi. Zbiór skończony z topologią dyskretną jest oczywiście zwarty. Z Twierdzenia Tichonowa wynika, że ![]() jest zbiorem zwartym w topologii produktowej.
jest zbiorem zwartym w topologii produktowej.
Ćwiczenie 2.8
Scharakteryzuj zbiory otwarte w powyższej topologii produktowej.
Ćwiczenie 2.9
Scharakteryzuj zbieżność ciągów w ![]()
Okazuje się, że wszystkie nieokresowe mozaiki przedstawione w poprzednim rozdziale, a co za tym idzie nieokresowe konfiguracje
stanu podstawowego w odpowiednim modelu gazu sieciowego, mają następującą własność. Niech ![]() będzie nieokresowym
pokryciem płaszczyzny. Dla każdego
będzie nieokresowym
pokryciem płaszczyzny. Dla każdego ![]() ,
, ![]() jest translacją
jest translacją ![]() o wektor
o wektor ![]() , to znaczy
, to znaczy ![]() .
Domknięcie w topologii produktowej zbioru wszystkich translacji
.
Domknięcie w topologii produktowej zbioru wszystkich translacji ![]() jest zbiorem wszystkich pokryć płaszczyzny
danymi typami dachówek. Zbiór ten, oznaczmy go przez
jest zbiorem wszystkich pokryć płaszczyzny
danymi typami dachówek. Zbiór ten, oznaczmy go przez ![]() , jest nośnikiem jedynej translacyjnie niezmienniczej miary
, jest nośnikiem jedynej translacyjnie niezmienniczej miary ![]() .
Miarę ta jest słabą granicą ciągu miar skupionych na kolejnych translacjach
.
Miarę ta jest słabą granicą ciągu miar skupionych na kolejnych translacjach ![]() ,
,
![]() ,
gdzie
,
gdzie ![]() jest miarą skupioną na
jest miarą skupioną na ![]() . Jedyność miary oznacza, że częstość występowania dowolnego skończonego układu dachówek
jest taka sama dla wszystkich pokryć i co więcej częstość ta jest zdefiniowana w sposób jednostajny. Niech
. Jedyność miary oznacza, że częstość występowania dowolnego skończonego układu dachówek
jest taka sama dla wszystkich pokryć i co więcej częstość ta jest zdefiniowana w sposób jednostajny. Niech ![]() i
i ![]() .
Częstość występowania wzoru
.
Częstość występowania wzoru ![]() w
w ![]() możemy obliczyć w następujący sposób. Niech
możemy obliczyć w następujący sposób. Niech ![]() będzie ciągiem kwadratów w
będzie ciągiem kwadratów w ![]() o środku w
o środku w ![]() i boku o długości
i boku o długości ![]() .
. ![]() jest liczbą translacji
jest liczbą translacji ![]() , które pokrywają się z lokalną konfiguracją
, które pokrywają się z lokalną konfiguracją ![]() . Mamy wtedy
. Mamy wtedy ![]() .
Zbieżność jest jednostajna ze względu na
.
Zbieżność jest jednostajna ze względu na ![]() , granica
, granica ![]() jest taka sama dla każdej nieokresowej mozaiki
jest taka sama dla każdej nieokresowej mozaiki ![]() i jest częstością występowania lokalnej konfiguracji
i jest częstością występowania lokalnej konfiguracji ![]() . Jest to jednocześnie prawdopodobieństwo występowania
. Jest to jednocześnie prawdopodobieństwo występowania ![]() w mierze
w mierze ![]() ,
,
![]() .
.
Chcielibyśmy aby istniała stała ![]() taka aby
taka aby
| (2.13) |
.
Okazuje się jednak, że we wszystkich przykładach mamy ![]() .
.
Czy istnieje skończony zbiór typów dachówek, pokrywający płaszczyznę tylko w sposób nieokresowy z jedyną translacyjnie niezmiennicza miarą ![]() o nośniku w zbiorze mozaik tak że jest spełniona własność 2.13.
o nośniku w zbiorze mozaik tak że jest spełniona własność 2.13.