Zagadnienia

1.1 Podstawy teoretyczne
1.2 Teoria zaburzeń dla macierzy niesymetrycznych
1.3 Teoria zaburzeń dla macierzy symetrycznych
- 1.3.1 Wrażliwość wartości własnych
- 1.3.2 Wrażliwość wektorów własnych

1. Zagadnienie własne I

Cztery początkowe wykłady poświęcimy zagadnieniu własnemu. Naszym zadaniem będzie obliczenie, a raczej numeryczna aproksymacja wartości własnych danej macierzy kwadratowej (jednej, kilku, lub wszystkich). W ogólniejszym sformułowaniu możemy chcieć obliczyć również odpowiednie wektory własne.

Pierwszy wykład będzie dotyczyć przede wszystkim wrażliwości wartości i wektorów własnych na zaburzenia macierzy. Jak wiemy z podstawowego wykładu analizy numerycznej, jest to istotne z punktu widzenia numerycznej jakości algorytmów.

1.1. Podstawy teoretyczne

Zaczniemy od przypomnienia podstawowych pojęć i faktów z algebry liniowej dotyczących zagadnienia własnego, z których skorzystamy w dalszej części wykładu.

Definicja 1.1

Liczbę $\lambda\in\mathbb{C}$ (zespoloną) nazywamy wartością własną macierzy kwadratowej $A\in\mathbb{C}^{{n,n}}$ jeśli istnieje niezerowy wektor $\vec{x}\in\mathbb{C}^{n}$ taki, że

$A\,\vec{x}\,=\,\lambda\,\vec{x}.$

Wektor $\vec{x}$ nazywamy wektorem własnym odpowiadającym wartości własnej $\lambda$ .

Równoważnie, $\lambda$ jest wartością własną macierzy $A$ gdy jest zerem jej wielomianu charakterystycznego, tzn. gdy wyznacznik

${\rm det}\left(A-\lambda\, I\right)\,=\, 0,$

gdzie $I$ jest macierzą identycznościową $n\times n$ . Krotnością algebraiczną wartości własnej $\lambda$ nazywamy jej krotność jako zera wielomianu charakterystycznego.

Zbiór wszystkich wektorów własnych odpowiadających danej wartości własnej $\lambda$ , uzupełniony o wektor zerowy, czyli zbiór $\{\vec{x}\in\mathbb{C}^{n}:\, A\,\vec{x}=\lambda\,\vec{x}\}$ , jest podprzestrzenią liniową $\mathbb{C}^{n}$ zwaną podprzestrzenią własną odpowiadającą $\lambda$ . Wymiar tej podprzestrzeni to krotność geometryczna wartości własnej $\lambda$ .

Wektory własne odpowiadające różnym wartościom własnym są liniowo niezależne.

Macierze $A,B\in\mathbb{C}^{{n,n}}$ są podobne gdy istnieje nieosobliwa macierz $C\in\mathbb{C}^{{n,n}}$ taka, że $B=C^{{-1}}\, A\, C$ . Oczywiście, relacja ,,bycia macierzami podobnymi” jest symetryczna.

Macierze podobne mają te same wartości własne. Jeśli bowiem $A\,\vec{x}=\lambda\,\vec{x}$ to $B\,(C\,\vec{x})=\lambda\,(C\,\vec{x})$ , tzn. $\lambda$ jest wartością własną $B$ , a odpowiadający jej wektor własny to $\vec{y}=C\,\vec{x}$ .

Macierz $A\in\mathbb{C}^{{n,n}}$ jest diagonalizowalna gdy jest podobna do macierzy diagonalnej, czyli gdy istnieje nieosobliwa $V=[\vec{v}_{1},\ldots,\vec{v}_{n}]\in\mathbb{C}^{{n,n}}$ taka, że

$V^{{-1}}\, A\, V\,=\,\Lambda\,=\,{\rm diag}(\lambda _{1},\lambda _{2},\ldots,\lambda _{n}).$

Zauważmy, że wtedy możemy równoważnie zapisać $A\, V=V\,\Lambda$ , albo $A\,\vec{v}_{j}=\lambda _{j}\,\vec{v}_{j}$ dla $1\le j\le n$ . Stąd elementy diagonalne macierzy $\Lambda$ są wartościami własnymi macierzy $A$ (gdzie ta sama wartość własna powtarza się tyle razy ile wynosi jej krotność), a kolumny macierzy $V$ są odpowiednimi wektorami własnymi.

Szczególne własności mają macierze hermitowskie albo, w przypadku rzeczywistym, macierze symetryczne, bowiem dla nich istnieją bazy ortonormalne (odpowiednio w $\mathbb{C}^{n}$ lub $\mathbb{R}^{n}$ ) wektorów własnych. Odpowiednie twierdzenie przypominamy jedynie w przypadku rzeczywistym, który ma zasadnicze znaczenie w obliczeniach praktycznych.

Twierdzenie 1.1

Niech $A$ będzie macierzą symetryczną o współczynnikach rzeczywistych,

$A\,=\, A^{T}\,\in\,\mathbb{R}^{{n,n}}.$

Wtedy istnieje w $\mathbb{R}^{n}$ baza ortonormalna wektorów własnych macierzy $A$ , tzn. istnieje układ wektorów własnych $\vec{q}_{1},\vec{q}_{2},\ldots,\vec{q}_{n}\in\mathbb{R}^{n}$ taki, że

$(\vec{q}_{i},\vec{q}_{j})_{2}\,=\,\vec{q}_{j}^{{\, T}}\,\vec{q}_{i}\,=\,\left\{\begin{array}[]{rl}0,&i\ne j,\\ 1,&i=j.\end{array}\right.$

Oczywiście, odpowiednie wartości własne $\lambda _{j}$ , $1\le j\le n$ , są też rzeczywiste.

Powyższa własność macierzy symetrycznych oznacza tyle, że są one diagonalizowalne przy pomocy macierzy ortogonalnych. Rzeczywiście, oznaczając

$Q\,:=\,[\vec{q}_{1},\vec{q}_{2},\ldots,\vec{q}_{n}],\qquad\Lambda\,=\,{\rm diag}(\lambda _{1},\lambda _{2},\ldots,\lambda _{n})$

mamy $Q^{T}\, Q=I=Q\, Q^{T}$ oraz

$Q^{T}\, A\, Q\,=\,\Lambda,\qquad A\,=\, Q\,\Lambda\, Q^{T}.$

1.2. Teoria zaburzeń dla macierzy niesymetrycznych

Zobaczmy najpierw, czy mamy w ogóle szansę numerycznego rozwiązania zadania znalezienia wartości własnych macierzy. W tym celu zbadamy jego uwarunkowanie, czyli wrażliwość na małe względne zaburzenia współczynników macierzy.

1.2.1. Wstępny przykład

W ogólności, uwarunkowanie naszego zadania może być niestety dowolnie duże.

Przykład 1.1

Niech macierz

$J_{\varepsilon}\,:=\,\left[\begin{array}[]{ccccc}\mu&1&0&\cdots&0\\ 0&\mu&1&&\vdots\\ \vdots&&\ddots&\ddots&0\\ 0&&&\mu&1\\ \varepsilon&0&\cdots&0&\mu\end{array}\right]\,\in\,\mathbb{C}^{{n,n}}.$

Dla $\varepsilon=0$ , macierz $J=J_{0}$ jest pojedynczą klatką Jordana, której jedyną wartością własną jest $\mu$ (o krotności algebraicznej $n$ i krotności geometrycznej $1$ ). Jeśli teraz zaburzymy wyraz w lewym dolnym rogu o $\varepsilon>0$ to otrzymana macierz $J_{\varepsilon}$ ma już $n$ różnych wartości własnych. Rzeczywiście, jej wielomian charakterystyczny

${\rm det}\left(J_{\varepsilon}-\lambda\, I\right)\,=\,(\mu-\lambda)^{n}+(-1)^{{n+1}}\varepsilon$

ma pierwiastki

$\mu _{k}=\mu+\varepsilon^{{1/n}}\cdot e^{{2\pi\imath k/n}},\qquad 0\le k\le n-1\qquad(\imath=\sqrt{-1}).$

Względne zaburzenie macierzy na poziomie $\varepsilon$ powoduje więc względne zaburzenie wartości własnych na poziomie $\varepsilon^{{1/n}}$ . Stąd, dla $n\ge 2$ , uwarunkowanie rośnie do $+\infty$ gdy $\varepsilon\to 0^{+}$ .

Oczywiście, otrzymane oszacowanie nie oznacza, że w powyższym przykładzie w ogóle nie potrafimy aproksymować wartości własnej. Tracimy jednak na liczbie poprawnie obliczonych cyfr znaczących wyniku. Niech $n=2$ . Wtedy przy dokładności arytmetyki $10^{{-8}}$ możemy spodziewać się jedynie wyniku z dokładnością do czterech cyfr znaczących, a przy dokładności $10^{{-16}}$ z dokładnością do ośmiu cyfr znaczących. Co więcej, im większy format $n$ klatki Jordana tym gorzej.

Powyższy przykład pokazuje również, że praktycznie niemożliwe jest numeryczne wyznaczenie struktury macierzy. Nawet drobne zaburzenie macierzy powoduje bowiem, że pojedyncza klatka Jordana staje się macierzą diagonalizowalną.

1.2.2. Wrażliwość wartości własnych

Dalej będziemy już zakładać, że macierz $A$ jest diagonalizowalna, czyli że jej postać Jordana jest macierzą diagonalną. Wtedy mamy następujące oszacowanie Bauera-Fike'a.

Twierdzenie 1.2

Niech $A\in\mathbb{C}^{{n,n}}$ będzie macierzą diagonalizowalną o wartościach własnych $\lambda _{k}$ , $1\le k\le n$ ,

$A\,=\, V\,\Lambda\, V^{{-1}}.$

Niech dalej $\mu$ będzie dowolną wartością własną macierzy `sąsiedniej' $A+E$ . Wtedy

$\min _{{1\le k\le n}}|\lambda _{k}-\mu|\,\le\,{\rm cond}(V)\cdot\| E\|,$

gdzie ${\rm cond}(V)=\| V\|\cdot\| V^{{-1}}\|$ oraz $\|\cdot\|$ jest normą macierzy indukowaną przez dowolną normę $p$ -tą wektora.

Dowód

Załóżmy bez zmniejszenia ogólności, że $\mu$ jest różne od każdej wartości własnej $\lambda _{k}$ . Niech $\vec{x}$ będzie wektorem własnym odpowiadającym wartości własnej $\mu$ macierzy $A+E$ . Wtedy

$V\,(\Lambda+V^{{-1}}\, E\, V)\, V^{{-1}}\,\vec{x}\,=\,\mu\,\vec{x}.$

(1.1)

Oznaczając $\vec{y}=V^{{-1}}\,\vec{x}\ne\vec{0}$ mamy dalej

$(\Lambda-\mu\, I)\,\vec{y}\,=\,-V^{{-1}}\, E\, V\,\vec{y},$

(1.2)

czyli

$\|\vec{y}\|\,\le\,\|\Lambda^{{-1}}\|\,\| V^{{-1}}\|\,\| V\|\,\| E\|\,\|\vec{y}\|.$

Ponieważ $\Lambda^{{-1}}={\rm diag}((\lambda _{1}-\mu)^{{-1}},\ldots,(\lambda _{n}-\mu)^{{-1}})$ to ostatecznie

$\min _{{1\le k\le n}}|\lambda _{k}-\mu|\,\le\,{\rm cond}(V)\,\| E\|.$

∎

Dla macierzy diagonalizowalnych zaburzenia wartości własnych są więc lipschitzowską funkcją zaburzeń macierzy, przy czym stała Lipschitza wynosi ${\rm cond}(V)$ .

Podane oszacowanie jest globalne dla wszystkich wartości własnych. Zaburzenia macierzy $A$ mogą jednak w różny sposób przenosić się na zaburzenia różnych wartości własnych. Od czego to zależy? Tak jak w dowodzie twierdzenia Bauera-Fike'a, niech

$(A+E)\,\vec{x}\,=\,\mu\,\vec{x},\qquad\|\vec{x}\| _{2}^{2}=\vec{x}^{{\, H}}\,\vec{x}=1.$

Biorąc jedynie $i$ -tą współrzędną po obu stronach równania (1.2) dostajemy

$(\lambda _{i}-\mu)\,\vec{z}_{i}^{{\, H}}\,\vec{x}\,=\,-\vec{z}_{i}^{{\, H}}\, E\,\vec{x},$

(1.3)

gdzie $\vec{z}_{i}$ jest znormalizowaną $i$ -tą kolumną macierzy

$(V^{{-1}})^{H}\,=\,[\vec{w}_{1},\vec{w}_{2},\ldots,\vec{w}_{n}],$

tzn. $\vec{z}_{i}=\vec{w}_{i}/\|\vec{w}_{i}\| _{2}$ . W szczególności, $\|\vec{z}_{i}\| _{2}=1$ oraz

$\vec{z}_{i}\,\perp\,{\rm span}(\vec{v}_{1},\ldots,\vec{v}_{{i-1}},\vec{v}_{{i+1}},\ldots,\vec{v}_{n})$

(ortogonalność ze względu na zwykły iloczyn skalarny). Stąd, jeśli $\vec{z}_{i}$ i $\vec{x}$ nie są ortogonalne to

$|\lambda _{i}-\mu|\,\le\,\frac{\| E\|}{|\vec{z}_{i}^{{\, H}}\,\vec{x}|}.$

Dla ustalenia uwagi załóżmy teraz, że minimum w twierdzeniu 1.2 jest osiągane dla $k=1$ , a podprzestrzenią własną wartości własnej $\lambda _{1}$ jest

${\mathcal{V}}\,=\,{\rm span}\{\vec{v}_{1},\vec{v}_{2},\ldots,\vec{v}_{s}\},$

gdzie wektory własne $\vec{v}_{1},\ldots,\vec{v}_{s}$ tworzą bazę ortonormalną w ${\mathcal{V}}$ . Jeśli wektor $\vec{x}$ jest `dostatecznie blisko' podprzestrzeni własnej ${\mathcal{V}}$ (co, jak pokażemy w następnym podrozdziale, jest prawdą dla dostatecznie małego zaburzenia $E$ ) to $|\lambda _{1}-\mu|$ można w przybliżeniu oszacować z góry przez maksymalną wartość wyrażenia

$\frac{\| E\|}{\max _{{1\le i\le s}}|\vec{z}_{i}^{{\, H}}\,\vec{y}|}$

po wszystkich $\vec{y}\in{\mathcal{V}}$ takich, że $\|\vec{y}\| _{2}=1$ . Niech więc $\vec{y}=\sum _{{i=1}}^{s}a_{i}\,\vec{v}_{i}\in{\mathcal{V}}$ , przy czym $\sum _{{i=1}}^{s}|a_{i}|^{2}=1$ . Wobec tego, że dla każdego $i$ mamy

$\vec{z}_{i}^{{\, H}}\,\vec{y}\,=\, a_{i}\,\vec{z}_{i}^{{\, H}}\,\vec{v}_{i}\,=\, a_{i}/\| w_{i}\| _{2},$

interesujące nas `max' jest najmniejsze gdy $a_{i}=\| w_{i}\| _{2}\left(\sum _{{j=1}}^{s}\| w_{j}\|^{2}\right)^{{-1/2}}$ . Stąd dostajemy

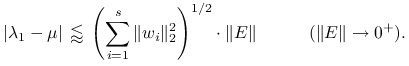$|\lambda _{1}-\mu|\,\lessapprox\,\left(\sum _{{i=1}}^{s}\| w_{i}\| _{2}^{2}\right)^{{1/2}}\cdot\| E\|\qquad\quad(\| E\|\to 0^{+}).$

Ponieważ $\| w_{i}\|=1/(\vec{z}_{i}^{{\, H}}\,\vec{v}_{i})$ oraz $\vec{z}_{i}$ jest ortogonalny do ${\rm span}\{\vec{v}_{j}:\, j\ne i\}$ , otrzymana nierówność sugeruje, że wartość własna $\lambda _{1}$ może być bardzo wrażliwa na zaburzenia macierzy gdy odpowiadająca jej podprzestrzeń własna ${\rm span}\{\vec{v}_{1},\ldots,\vec{v}_{s}\}$ jest `prawie ortogonalna' do ${\rm span}\{\vec{v}_{{s+1}},\ldots,\vec{v}_{n}\}^{\perp}$ . Dobrze ilustruje to następujący przykład.

Przykład 1.2

Rozpatrzmy macierz

$A\,=\,\left[\begin{array}[]{cc}2&-1/\delta\\ 0&1\end{array}\right],$

gdzie $\delta>0$ jest `małe'. Wartości własne $A$ wynoszą $1$ i $2$ , natomiast wektory własne $[1,0]^{T}$ i $[1,\delta]^{T}$ są prawie liniowo zależne. Zaburzając macierz przez dodanie $\varepsilon=-2\delta$ do wyrazu w lewym dolnym rogu dostajemy macierz o wartościach własnych $0$ i $3$ , a odpowiadające im wektory własne wynoszą $[1,2\delta]^{T}$ i $[1,-2\delta]^{T}$ . Dodajmy, że w tym przypadku ${\rm cond}(V)$ jest proporcjonalne do $1/\delta$ .

1.2.3. Wrażliwość wektorów własnych

Przez zaburzenie wektora własnego będziemy rozumieć odległość wektora $\vec{x}$ od podprzestrzeni własnej ${\mathcal{V}}$ , tzn.

${\rm dist}(\vec{x},{\mathcal{V}})\,:=\,\min\,\{\,\|\vec{x}-\vec{v}\| _{2}:\,\;\vec{v}\in{\mathcal{V}}\,\},$

albo, równoważnie, długość rzutu ortogonalnego $P\vec{x}$ wektora $\vec{x}$ na podprzestrzeń

${\mathcal{V}}^{\perp}\,=\,{\rm span}(\vec{z}_{{s+1}},\ldots,\vec{z}_{n}).$

Pokażemy, że podobnie jak przypadku wartości własnych, zaburzenie wektorów własnych jest lipszitzowską funkcją $\| E\|$ . W tym celu, wybierzmy w ${\mathcal{V}}^{\perp}$ dowolną bazę ortonormalną

$Y\,=\,[\vec{y}_{{s+1}},\ldots,\vec{y}_{n}]\in\mathbb{C}^{{n,n-s}}.$

Niech $B^{H}\in\mathbb{C}^{{n-s,n-s}}$ będzie macierzą przejścia z bazy $Z=[\vec{z}_{{s+1}},\ldots,\vec{z}_{n}]$ do $Y$ ,

$Y\,=\, Z\, B^{H}.$

Wtedy

$\| P\vec{x}\| _{2}\,=\,\| Y^{H}\, P\vec{x}\| _{2}\,=\,\| B\, Z^{H}\, P\vec{x}\| _{2}.$

Wobec równości (1.3) mamy

$Z^{H}\, P\vec{x}\,=\,-{\rm diag}\left((\lambda _{{s+1}}-\mu)^{{-1}},\ldots,(\lambda _{n}-\mu)^{{-1}}\right)\, B^{{-1}}\, Y^{H}\, E\,\vec{x}.$

Ponieważ na podstawie twierdzenia Bauera-Fike'a mamy

$|\lambda _{1}-\mu|\,\ge\,|\lambda _{i}-\lambda _{1}|-|\lambda _{1}-\mu|\,\ge\,|\lambda _{i}-\lambda _{1}|-{\rm cond}(V)\cdot\| E\|,$

otrzymujemy następującą przybliżoną nierówność

${\rm dist}(\vec{x},{\mathcal{V}})\,=\,\| P\vec{x}\| _{2}\,\lessapprox\,\frac{\| B\| _{2}\| B^{{-1}}\| _{2}}{\min _{{s+1\le i\le n}}|\lambda _{i}-\lambda _{1}|}\,\| E\|\qquad\quad(\| E\|\to 0^{+}).$

(1.4)

Uwaga. W przykładzie 1.2 istotnemu zaburzeniu uległy wartości własne, natomiast wektory własne nie. Jest to zrozumiałe w świetle ostatniego wyniku. W przypadku macierzy $2\times 2$ mamy bowiem $B=1\in\mathbb{C}^{{1,1}}$ i w konsekwencji wrażliwość wektorów własnych zależy tylko od różnicy $|\lambda _{1}-\lambda _{2}|$ .

Poniższy przykład dla macierzy symetrycznej (!) pokazuje jak ważne dla wrażliwości wektorów własnych jest odseparowanie różnych wartości własnych.

Przykład 1.3

Wartościami własnymi macierzy symetrycznej

$A\,=\,\left[\begin{array}[]{cc}1+\varepsilon&0\\ 0&1\end{array}\right]$

są $(1+\varepsilon)$ i $1$ , a odpowiadająca baza wektorów własnych to $\vec{e}_{1}$ i $\vec{e}_{2}$ . Dla macierzy zaburzonej na poziomie $\varepsilon$ (czyli różnicy wartości własnych),

$A+E\,=\,\left[\begin{array}[]{cc}1+\varepsilon&0\\ 0&1\end{array}\right]+\varepsilon\,\left[\begin{array}[]{rr}-1&1\\ 1&0\end{array}\right],$

wartościami własnymi są $(1+\varepsilon)$ i $(1-\varepsilon)$ , a bazę wektorów własnych tworzą $\vec{e}_{1}+\vec{e}_{2}$ i $\vec{e}_{1}-\vec{e}_{2}$ . Baza wektorów własnych została obrócona o możliwie maksymalny kąt $\pi/4$ .

1.3. Teoria zaburzeń dla macierzy symetrycznych

W tej części będziemy zakładać, że macierz jest rzeczywista i symetryczna,

$A\,=\, A^{T}\,\in\,\mathbb{R}^{{n,n}}.$

Ponieważ elementy $a_{{i,j}}$ i $a_{{j,i}}$ macierzy $A$ są w praktycznych obliczeniach reprezentowane przez tą samą zmienną, zasadne jest założenie, że macierz zaburzona $A+E$ jest również symetryczna, $E=E^{T}\in\mathbb{R}^{{n,n}}$ .

1.3.1. Wrażliwość wartości własnych

Przypomnijmy twierdzenie 1.1, które mówi, że dla macierzy symetrycznej istnieje baza ortonormalna $Q$ jej wektorów własnych. Ponieważ dla macierzy ortogonanych mamy $\| Q\| _{2}=1$ ,

${\rm cond}_{2}(Q)\,=\,\| Q\| _{2}\| Q^{T}\| _{2}\,=\, 1.$

To zaś, razem z twierdzeniem 1.2 implikuje, że każda watość własna $\mu$ macierzy sąsiedniej $A+E$ spełnia nierówność

$\min _{{1\le i\le n}}|\lambda _{i}-\mu|\,\le\,\| E\| _{2}.$

Możemy jednak pokazać dużo więcej. Zachodzi bowiem następujące twierdzenie Weyla.

Twierdzenie 1.3

Niech $\lambda _{1}\ge\lambda _{2}\ge\cdots\ge\lambda _{n}$ będą wartościami własnymi macierzy $A=A^{T}\in\mathbb{R}^{{n,n}}$ , a $\mu _{1}\ge\mu _{2}\ge\cdots\ge\mu _{n}$ wartościami własnymi macierzy sąsiedniej $A+E$ , gdzie $E=E^{T}\in\mathbb{R}^{{n,n}}$ . Wtedy dla wszystkich $1\le k\le n$ mamy

$|\lambda _{k}-\mu _{k}|\,\le\,\| E\| _{2}.$

Dowód twierdzenia opiera się na następującej pożytecznej nierówności.

Lemat 1.1

Dla dowolnej rzeczywistej macierzy symetrycznej $A$ mamy

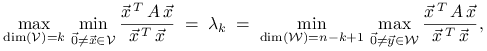$\max _{{{\rm dim}({\mathcal{V}})=k}}\,\min _{{\vec{0}\ne\vec{x}\in{\mathcal{V}}}}\frac{\vec{x}^{{\, T}}\, A\,\vec{x}}{\vec{x}^{{\, T}}\,\vec{x}}\;=\;\lambda _{k}\;=\;\min _{{{\rm dim}({\mathcal{W}})=n-k+1}}\,\max _{{\vec{0}\ne\vec{y}\in{\mathcal{W}}}}\frac{\vec{x}^{{\, T}}\, A\,\vec{x}}{\vec{x}^{{\, T}}\,\vec{x}},$

(1.5)

przy czym odpowiednie maksimum i minimum osiągane są dla ${\mathcal{V}}^{*}={\rm span}(\vec{v}_{k},\vec{v}_{{k+1}},\ldots,\vec{v}_{n})$ oraz ${\mathcal{W}}^{*}={\rm span}(\vec{v}_{1},\vec{v}_{2},\ldots,\vec{v}_{k})$ .

Dowód

Niech ${\mathcal{V}}$ i ${\mathcal{W}}$ będą dowolnymi podprzestrzeniami o wskazanych wymiarach. Ponieważ suma wymiarów wynosi $n+1$ to istnieje wektor niezerowy $\vec{z}\in{\mathcal{V}}\cap{\mathcal{W}}$ . W konsekwencji

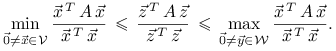$\min _{{\vec{0}\ne\vec{x}\in{\mathcal{V}}}}\frac{\vec{x}^{{\, T}}\, A\,\vec{x}}{\vec{x}^{{\, T}}\,\vec{x}}\,\le\,\frac{\vec{z}^{{\, T}}\, A\,\vec{z}}{\vec{z}^{{\, T}}\,\vec{z}}\,\le\,\max _{{\vec{0}\ne\vec{y}\in{\mathcal{W}}}}\frac{\vec{x}^{{\, T}}\, A\,\vec{x}}{\vec{x}^{{\, T}}\,\vec{x}}.$

Biorąc maximum po ${\mathcal{V}}$ i minimum po ${\mathcal{W}}$ dostajemy, że w (1.5) lewa strona nie jest większa od prawej. Aby pokazać odwrotną nierówność, zauważmy, że dla ${\mathcal{V}}^{*}$ i ${\mathcal{W}}^{*}$ mamy odpowiednio

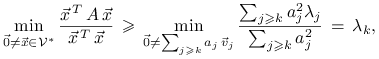$\min _{{\vec{0}\ne\vec{x}\in{\mathcal{V}}^{*}}}\frac{\vec{x}^{{\, T}}\, A\,\vec{x}}{\vec{x}^{{\, T}}\,\vec{x}}\,\ge\,\min _{{\vec{0}\ne\sum _{{j\ge k}}a_{j}\,\vec{v}_{j}}}\frac{\sum _{{j\ge k}}a_{j}^{2}\lambda _{j}}{\sum _{{j\ge k}}a_{j}^{2}}\,=\,\lambda _{k},$

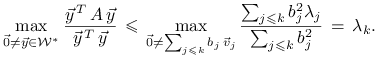$\max _{{\vec{0}\ne\vec{y}\in{\mathcal{W}}^{*}}}\frac{\vec{y}^{{\, T}}\, A\,\vec{y}}{\vec{y}^{{\, T}}\,\vec{y}}\,\le\,\max _{{\vec{0}\ne\sum _{{j\le k}}b_{j}\,\vec{v}_{j}}}\frac{\sum _{{j\le k}}b_{j}^{2}\lambda _{j}}{\sum _{{j\le k}}b_{j}^{2}}\,=\,\lambda _{k}.$

∎

Dla dowodu twierdzenia 1.3 zastosujemy lemat 1.5 najpierw do macierzy $A+E$ , a potem do macierzy $A=(A+E)-E$ . Otrzymujemy odpowiednio

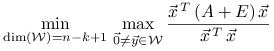$\displaystyle\mu _{k}$	$\displaystyle=$	$\displaystyle\min _{{{\rm dim}({\mathcal{W}})=n-k+1}}\,\max _{{\vec{0}\ne\vec{y}\in{\mathcal{W}}}}\frac{\vec{x}^{{\, T}}\,(A+E)\,\vec{x}}{\vec{x}^{{\, T}}\,\vec{x}}$
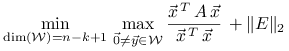	$\displaystyle\le$	$\displaystyle\min _{{{\rm dim}({\mathcal{W}})=n-k+1}}\,\max _{{\vec{0}\ne\vec{y}\in{\mathcal{W}}}}\frac{\vec{x}^{{\, T}}\, A\,\vec{x}}{\vec{x}^{{\, T}}\,\vec{x}}\,+\\| E\\| _{2}$
	$\displaystyle=$	$\displaystyle\lambda _{k}\,+\,\\| E\\| _{2},$

oraz podobnie nierówność odwrotną $\lambda _{k}\,\le\,\mu _{k}+\| E\| _{2}$ , czyli ostatecznie

$|\lambda _{k}-\mu _{k}|\,\le\,\| E\| _{2}.$

Zanotujmy jeszcze, że wielkość

$\frac{\vec{x}^{{\, T}}\, A\,\vec{x}}{\vec{x}^{{\, T}}\,\vec{x}}$

znana jest pod nazwą ilorazu Rayleigh'a.

1.3.2. Wrażliwość wektorów własnych

Niech ${\mathcal{V}}_{k}\subset\mathbb{R}^{n}$ będzie podprzestrzenią własną odpowiadającą wartości własnej $\lambda _{k}$ macierzy $A$ , a $\vec{x}_{k}$ wektorem własnym odpowiadającym wartości własnej $\mu _{k}$ macierzy sąsiedniej $A+E$ . Niech dalej $\theta _{k}$ będzie kątem pomiędzy $\vec{x}_{k}$ i podprzestrzenią ${\mathcal{V}}_{k}$ . Wtedy

$\sin\theta _{k}\;\lessapprox\;\frac{\| E\| _{2}}{\min _{{\lambda _{j}\ne\lambda _{k}}}|\lambda _{k}-\lambda _{j}|}\qquad\quad(\| E\| _{2}\to 0^{+}).$

Rzeczywiście, to wynika bezpośrednio z twierdzenia 1.3, nierówności (1.4) oraz faktu, że macierz $B$ w (1.4) jest identycznością. Pokażemy teraz nierówność dokładną.

Twierdzenie 1.4

$\frac{1}{2}\sin 2\theta _{k}\;\le\;\frac{\| E\| _{2}}{\min _{{\lambda _{j}\ne\lambda _{k}}}|\lambda _{k}-\lambda _{j}|}.$

Dowód

Dla ustalenia uwagi załóżmy, że $k=1$ oraz odpowiednia podprzestrzeń własna ${\mathcal{V}}_{1}={\rm span}(\vec{v}_{1},\ldots,\vec{v}_{s})$ . Przedstawmy wektor własny $\vec{x}_{1}$ , $\|\vec{x}\| _{2}=1$ , w jednoznaczny sposób w postaci

$\vec{x}_{1}\,=\,\vec{v}+\vec{d},$

gdzie $\vec{v}\in{\mathcal{V}}_{1}$ i $\vec{d}\in{\mathcal{V}}_{1}^{\perp}$ ,

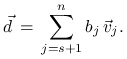$\vec{d}\,=\,\sum _{{j=s+1}}^{n}b_{j}\,\vec{v}_{j}.$

Możemy też założyć, bez straty ogólności, że $\vec{d}\ne\vec{0}$ i $\vec{x}_{1}\notin{\mathcal{V}}_{1}^{\perp}$ , tzn. $0<\theta<\pi/2$ .

Przekształcając równanie $(A+E)\,(\vec{v}+\vec{d})=\mu _{1}\,(\vec{v}+\vec{d})$ dostajemy

$\vec{z}\,:=\,(A-\lambda _{1}\, I)\,\vec{d}\,=\,\left((\mu _{1}-\lambda _{1})\, I-E\right)\,(\vec{v}+\vec{d}).$

Ponieważ każdy z wektorów $\vec{v}_{i}$ dla $1\le i\le s$ należy do jądra macierzy symetrycznej $A-\lambda _{1}\, I$ to wektor $(A-\lambda _{1}\, I)\,\vec{d}$ jest ortogonalny do ${\mathcal{V}}_{1}$ i tym samym możemy zapisać

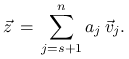$\vec{z}\,=\,\sum _{{j=s+1}}^{n}a_{j}\,\vec{v}_{j}.$

Mamy dalej

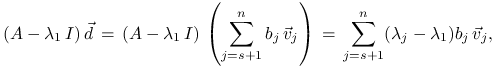$(A-\lambda _{1}\, I)\,\vec{d}\,=\,(A-\lambda _{1}\, I)\,\left(\sum _{{j=s+1}}^{n}b_{j}\,\vec{v}_{j}\right)\,=\,\sum _{{j=s+1}}^{n}(\lambda _{j}-\lambda _{1})b_{j}\,\vec{v}_{j},$

a stąd $a_{j}=(\lambda _{j}-\lambda _{1})b_{j}$ i

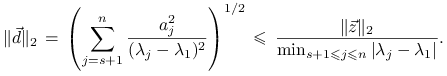$\|\vec{d}\| _{2}\,=\,\left(\sum _{{j=s+1}}^{n}\frac{a_{j}^{2}}{(\lambda _{j}-\lambda _{1})^{2}}\right)^{{1/2}}\,\le\,\frac{\|\vec{z}\| _{2}}{\min _{{s+1\le j\le n}}|\lambda _{j}-\lambda _{1}|}.$

Z kolei z równości $\vec{v}^{{\, T}}\,\left((\mu _{1}-\lambda _{1})\, I-E\right)\,(\vec{v}+\vec{d})=0$ dostajemy

$(\mu _{1}-\lambda _{1})\,\|\vec{v}\| _{2}^{2}\,=\,\vec{v}^{{\, T}}\, E\,(\vec{v}+\vec{d}),$

skąd

$\vec{z}\,=\,\frac{1}{\|\vec{v}\| _{2}^{2}}(\vec{v}+\vec{d})\,\vec{v}^{{\, T}}\, E\,(\vec{v}+\vec{d})-E\,(\vec{v}+\vec{d})\,=\,\left(\frac{1}{\|\vec{v}\| _{2}^{2}}(\vec{v}+\vec{d})\,\vec{v}^{{\, T}}-I\right)\, E\,(\vec{v}+\vec{d}).$

Gdybyśmy teraz wiedzieli, że

$\left\|\frac{1}{\|\vec{v}\| _{2}^{2}}(\vec{v}+\vec{d})\,\vec{v}^{{\, T}}-I\right\| _{2}\,=\,\frac{1}{\|\vec{v}\| _{2}}$

(1.6)

to moglibyśmy napisać

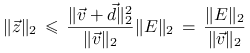$\|\vec{z}\| _{2}\,\le\,\frac{\|\vec{v}+\vec{d}\| _{2}^{2}}{\|\vec{v}\| _{2}}\| E\| _{2}\,=\,\frac{\| E\| _{2}}{\|\vec{v}\| _{2}}$

i ostatecznie

$\frac{1}{2}\sin 2\theta _{1}\,=\,\sin\theta _{1}\cos\theta _{1}\,=\,\|\vec{d}\| _{2}\|\vec{v}\| _{2}\,\le\,\frac{\|\vec{z}\| _{2}\|\vec{v}\| _{2}}{\min _{{s+1\le j\le n}}|\lambda _{j}-\lambda _{1}|}\,\le\,\frac{\| E\| _{2}}{\min _{{s+1\le j\le n}}|\lambda _{j}-\lambda _{1}|}.$

Pozostaje więc do pokazania równość (1.6). W tym celu, weźmy $\vec{y}=\alpha\,\vec{v}/\|\vec{v}\| _{2}+\beta\,\vec{h}$ , gdzie $\| h\| _{2}=1$ , $\vec{h}\perp\vec{v}$ i $\|\vec{y}\| _{2}=(\alpha^{2}+\beta^{2})^{{1/2}}=1$ . Wtedy

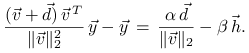$\frac{(\vec{v}+\vec{d})\,\vec{v}^{{\, T}}}{\|\vec{v}\| _{2}^{2}}\,\vec{y}-\vec{y}\,=\,\frac{\alpha\,\vec{d}}{\|\vec{v}\| _{2}}-\beta\,\vec{h}.$

Dla danych $\alpha$ i $\beta$ , wektor po prawej stronie ma największą normę gdy $\vec{h}=\pm\vec{d}/\|\vec{d}\| _{2}$ , przy czym bierzemy plus wtedy i tylko wtedy gdy $\alpha$ i $\beta$ mają różne znaki. Dlatego poszukiwana norma wynosi

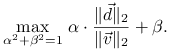$\max _{{\alpha^{2}+\beta^{2}=1}}\,\alpha\cdot\frac{\|\vec{d}\| _{2}}{\|\vec{v}\| _{2}}+\beta.$

Zamieniając zmienne na $\alpha=\cos\phi$ , $\beta=\sin\phi$ łatwo dostajemy, że optymalne $\phi\in(0,\pi/2)$ spełnia $\sin\phi=\|\vec{d}\| _{2}$ , $\cos\phi=\|\vec{v}\| _{2}$ , a stąd dostajemy wynik

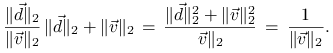$\frac{\|\vec{d}\| _{2}}{\|\vec{v}\| _{2}}\,\|\vec{d}\| _{2}+\|\vec{v}\| _{2}\,=\,\frac{\|\vec{d}\| _{2}^{2}+\|\vec{v}\| _{2}^{2}}{\vec{v}\| _{2}}\,=\,\frac{1}{\|\vec{v}\| _{2}}.$

∎

Pokazaliśmy, że wektory własne są mało wrażliwe na zaburzenia macierzy o ile wartości własne są odseparowane od siebie na poziomie dużo większym niż $\| E\| _{2}$ . W szczególności, jeśli dodatkowo $\lambda _{i}\ne\lambda _{j}$ , $i\ne j$ , to mamy jednolite oszacowanie

$\frac{1}{2}\,\sin 2\theta _{k}\,\le\,\frac{\| E\| _{2}}{\min _{{i\ne j}}|\lambda _{i}-\lambda _{j}|}.$

Przypomnijmy jeszcze przykład 1.3 pokazujący, że warunek odseparowania wartości własnych jest konieczny.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Matematyka obliczeniowa II

Zagadnienia

1. Zagadnienie własne I

1.1. Podstawy teoretyczne

Definicja 1.1

Twierdzenie 1.1

1.2. Teoria zaburzeń dla macierzy niesymetrycznych

1.2.1. Wstępny przykład

Przykład 1.1

1.2.2. Wrażliwość wartości własnych

Twierdzenie 1.2

Dowód

Przykład 1.2

1.2.3. Wrażliwość wektorów własnych

Przykład 1.3

1.3. Teoria zaburzeń dla macierzy symetrycznych

1.3.1. Wrażliwość wartości własnych

Twierdzenie 1.3

Lemat 1.1

Dowód

1.3.2. Wrażliwość wektorów własnych

Twierdzenie 1.4

Dowód