Zagadnienia

12.1 Metoda nawrotów
- 12.1.1 Prosta metoda nawrotów
- 12.1.2 Wielomianowe nawroty
12.2 Metody kontynuacji
- 12.2.1 Wyznaczanie dobrego przybliżenia początkowego dla metody typu Newtona
- 12.2.2 Metoda homotopii

12. Globalizacja zbieżności

Zarówno metoda Newtona, jak i omawiane przez nas jej modyfikacje, mogą zawieść (to znaczy: mogą nie być zbieżne lub dobrze określone), gdy początkowe przybliżenie $x_{0}$ będzie zbyt daleko od rozwiązania i założenia standardowe nie będą spełnione w $x_{0}$ . Ponieważ zwykle trudno wiedzieć a priori, czy jesteśmy dostatecznie blisko rozwiązania, opracowano szereg mniej lub bardziej heurystycznych technik globalizacji zbieżności metod typu Newtona, pozwalających w końcu dotrzeć w takie pobliże rozwiązania, w którym już nastąpi szybka zbieżność.

Podobny charakter ma inny — jakże często spotykany w zastosowaniach — problem: równanie nieliniowe z parametrem, w którym celem jest wyznaczenie nie jednego, jak dotychczas, ale całej rodziny rozwiązań (w zależności od parametru). Przykładowo, mogłaby nas interesować charakterystyka prądowo–napięciowa pewnego układu elektronicznego o nieliniowych własnościach: wtedy dla zadanych wartości napięcia musielibyśmy rozwiązać równanie nieliniowe, określające prąd w obwodzie. Ponieważ aby narysować dokładny wykres takiej charakterystyki, należałoby próbkować wartości natężenia w bardzo wielu (powiedzmy, kilkuset) podanych napięciach — dobrze byłoby te kilkaset układów równań rozwiązać możliwie efektywnie. Pokażemy więc pożyteczną metodę wyznaczania bardzo dobrych punktów startowych $x_{0}$ w przypadku, gdy zależność rozwiązania od parametru jest dostatecznie regularna.

Co ciekawe, tę technikę można wykorzystać także w celu globalizacji zbieżności metody typu Newtona dla pojedynczego równania nieliniowego!

12.1. Metoda nawrotów

Przypomnijmy, że rozważane przez nas metody iteracyjne są postaci

$x_{{k+1}}=x_{k}-s.$

Zacznijmy od prostej obserwacji, że — gdy $x_{k}$ jest daleko od rozwiązania — poprawka $s=F^{{\prime}}(x_{k})^{{-1}}F(x_{k})$ jest co prawda słuszna co do kierunku (idziemy wszak w stronę, w którą funkcja lokalnie maleje), ale być może przesadna co do wielkości i spowodować, że w następnej iteracji wartość residuum wzrośnie, a nie zmaleje…

Metoda nawrotów (ang. backtracking) reprezentuje prostą strategię, polegającą na zachowaniu kierunku poprawki i następnie na ewentualnym jej skróceniu tak, by residuum w $x_{{k+1}}$ było mniejsze od residuum w $x_{k}$ : dzięki temu zawsze będziemy redukować $\| F(x)\|$ w nadziei, że tym samym będziemy zbliżać się do rozwiązania.

12.1.1. Prosta metoda nawrotów

W swojej najbardziej podstawowej (raczej nie stosowanej) postaci, metoda nawrotów wyznacza poprawkę $s$ następująco:

Metoda nawrotów, wersja bazowa

$s=F^{{\prime}}(x_{k})^{{-1}}F(x_{k})$ ; {zaczynamy od standardowej poprawki z metody Newtona}

TEST: $x=x_{k}-s$ ; {wypróbowujemy poprawkę}

if $\| F(x)\|<\| F(x_{k})\|$ then

$x_{{k+1}}=x$ ; {akceptujemy poprawkę}

else begin

$s=s/2$ ; {skracamy poprawkę i ponownie sprawdzamy}

goto TEST;

end

W praktyce powyższe kryterium akceptacji poprawki $\| F(x)\|<\| F(x_{k})\|$ może być zbyt łagodne i dlatego raczej stosuje się tzw. regułę Armijo:

Metoda nawrotów z regułą Armijo

$s=F^{{\prime}}(x_{k})^{{-1}}F(x_{k})$ ;

$\lambda=1$ ; {mnożnik poprawki}

TEST: $x=x_{k}-\lambda s$ ; {wypróbowujemy poprawkę}

if $\| F(x)\|<(1-\alpha\lambda)\| F(x_{k})\|$ then

$x_{{k+1}}=x$ ; {akceptujemy poprawkę}

else begin

$\lambda=\lambda/2$ ; {zmniejszamy mnożnik i ponownie sprawdzamy}

goto TEST;

end

Parametr relaksacyjny $\alpha$ dobiera się na wyczucie, zwykle trochę poniżej jedności. Oczywiście, nie można dać się zwariować i stosować zbyt małych mnożników $\lambda$ , bo prowadziłoby to do stagnacji metody (lepiej potraktować to jako informację o kłopotach ze zbieżnością i następnie restartować metodę z zupełnie innym $x_{0}$ ).

Metoda nawrotów, jakkolwiek często istotnie poprawia charakter zbieżności metody Newtona, może także załamać się, gdy $F^{{\prime}}(x_{k})$ stanie się osobliwa. Nie musi także gwarantować zbieżności do prawdziwego rozwiązania, gdyż może zdarzyć się, że na przykład

iteracje 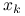$x_{k}$ dążą do lokalnego ekstremum 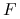$F$ , a nie do miejsca zerowego;
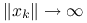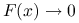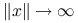$\| x_{k}\|\rightarrow\infty$ (bo na przykład $F(x)\rightarrow 0$ dla $\| x\|\rightarrow\infty$ ).

12.1.2. Wielomianowe nawroty

Zamiast stosować dość prymitywną regułę wyznaczania nowego mnożnika poprawki: $\lambda=\lambda/2$ , można wybierać nowe $\lambda$ jako argument minimalizujący wartość wielomianu interpolacyjnego dla funkcji $g(\lambda)=\| F(x_{k}-\lambda s)\|$ , opartego na węzłach będących poprzednio wybieranymi wartościami $\lambda$ . Taką strategię nazywa się strategią nawrotów wielomianowych. Inna metoda — obszaru ufności (ang. trust region) — pozwala dobrać nie tylko mnożnik poprawki, ale dodatkowo nieco zmienić jej kierunek; jest więc nieco bardziej elastyczna, ale za cenę wyższego kosztu.

Przykład 12.1 (Metoda wielomianowych nawrotów oparta na dwóch punktach)

Wybierając

$g(\lambda)=\| F(x_{k}-\lambda s)\| _{2}^{2},$

po teście $\lambda=1$ , dysponujemy następującymi trzema(!) wartościami $g$ :

	$\displaystyle g(0)$	$\displaystyle=\\| F(x_{k})\\| _{2}^{2}\text{ (z poprzedniego kroku)},$
	$\displaystyle g^{{\prime}}(0)$	$\displaystyle=g^{{\prime}}(\lambda)_{{\|_{{\lambda=0}}}}=-2F(x_{k})^{T}F^{{\prime}}(x_{k})s,$
	$\displaystyle g(1)$	$\displaystyle=\\| F(x_{k}-s)\\| _{2}^{2}.$

Zauważmy, że jeśli $s$ było wyznaczone metodą Newtona, to wtedy faktycznie $g^{{\prime}}(0)<0$ , a więc $F(x_{k})$ maleje w kierunku $s$ . Na podstawie tych trzech wartości możemy skonstruować wielomian interpolacyjny (Hermite'a) drugiego stopnia oraz wyznaczyć $\lambda _{{\text{nowe}}}$ , minimalizujące ten wielomian:

$\lambda _{{\text{nowe}}}=-\dfrac{1}{2}\dfrac{g^{{\prime}}(0)}{g(1)-g(0)-g^{{\prime}}(0)}.$

Ćwiczenie 12.1

Wyprowadź powyższy wzór na $\lambda _{{\text{nowe}}}$ .

Wskazówka:

Wspominany wielomian interpolacyjny Hermite'a dla $g$ to

$w(\lambda)=g(0)+g^{{\prime}}(0)\lambda+(g(1)-g(0)-g^{{\prime}}(0))\lambda^{2}.$

Dla metody Broydena także można sformułować regułę podobną do reguły Armijo dla metody Newtona, [9].

Jeszcze innym sposobem globalizacji zbieżności metody Newtona może być wykorzystanie metody kontynuacji — o czym w następnym rozdziale.

12.2. Metody kontynuacji

W wielu praktycznych zastosowaniach mamy do czynienia nie z jednym równaniem nieliniowym, ale z całą rodziną równań, indeksowaną pewnym parametrem (lub zestawem parametrów). Dla ustalenia uwagi, rozważmy więc rodzinę równań indeksowaną parametrem $t\in[0,1]$ ,

$H(x,t)=0,$

(12.1)

gdzie $H:D\times[0,1]\rightarrow\mathbb{R}^{N}$ , gdzie $D$ jest otwartym niepustym podzbiorem $\mathbb{R}^{N}$ .

W ogólności zbiór wszystkich rozwiązań (12.1) może być dziwaczny, ale my zajmiemy się regularnym — spotykanym w niektórych zastosowaniach — przypadkiem, kiedy możemy lokalnie jednoznacznie określić funkcję $t\mapsto x(t)$ taką, że

$H(x(t),t)=0.$

Dokładniej, załóżmy, że $H\in C^{1}(D\times[0,1])$ i dla pewnego parametru $t^{*}\in(0,1)$ i dla pewnego $x^{*}\in D$ zachodzi

$H(x^{*},t^{*})=0.$

Jeśli dodatkowo założymy, że pochodna cząstkowa $H_{{x}}(x^{*},t^{*})$ jest nieosobliwa, to na mocy twierdzenia o funkcji uwikłanej istnieje $U=(t^{*}-\epsilon,t^{*}+\epsilon)$ , gdzie $\epsilon>0$ , takie, że dla $t\in U$ jest jednoznacznie wyznaczone rozwiązanie $x(t)$ ,

$H(x(t),t)=0.$

Ponadto, $x\in C^{1}(U)$ oraz

$\displaystyle x^{{\prime}}(t)=-H_{{x}}(x(t),t)^{{-1}}H_{{t}}(x(t),t)\qquad\text{ dla }t\in U.$

(12.2)

Mówimy w takim przypadku, że $x(t)$ jest regularną gałęzią rozwiązań (12.1), przechodzącą przez $(x^{*},t^{*})$ . W dalszym ciągu zajmiemy się właśnie metodami wyznaczania takiej regularnej gałęzi rozwiązań.

12.2.1. Wyznaczanie dobrego przybliżenia początkowego dla metody typu Newtona

Przypuśćmy, że dla parametru $t^{*}$ wyznaczyliśmy już rozwiązanie $x^{*}=x(t^{*})$ . Naszym zadaniem jest wyznaczenie $x(t^{*}+h)$ , gdzie $h>0$ jest małe¹⁵W szczególności, $t^{*}+h\in U$ .. Odpowiada to wziętej z życia sytuacji, gdy chcemy prześledzić przebieg gałęzi $x(t)$ , próbkując jej wartości dla kolejnych (zapewne gęsto rozmieszczonych w $U$ ) wartości parametru $t$ .

Naturalnie, do wyznaczenia $x(t^{*}+h)$ możemy użyć dowolnej z wcześniej opisywanych metod — ale czy nie udałoby się wykorzystać informacji uzyskanej dla $t^{*}$ w celu wyznaczenia przybliżenia $x_{0}$ dla $x(t^{*}+h)$ tak, by metoda Newtona od razu startowała z dobrego przybliżenia początkowego? Ze względu na regularny charakter gałęzi $x(t)$ nietrudno zgadnąć, że niezłym przybliżeniem dla $x(t^{*}+h)$ mogłoby być $x_{0}=x^{*}$ . Rzeczywiście, niech

$l=\max _{{t\in[t^{*},t^{*}+h]}}\| x^{{\prime}}(t)\|.$

Wtedy (na mocy lematu o wartości średniej 9.1)

$\| x(t^{*}+h)-x^{*}\|\leq l|h|,$

więc jeśli $h$ jest dostatecznie małe względem $l$ , to $x_{0}$ będzie dostatecznie blisko $x(t^{*}+h)$ , by zagwarantować szybką (kwadratową) zbieżność metody Newtona (pod oczywistym warunkiem, że spełnione są założenia standardowe, por. rozdział 9.3.1). Ten sposób wyboru $x_{0}$ , zaproponowany przez Poincaré'go, nazywa się klasyczną metodą kontynuacji.

Można jednak, niewiele większym kosztem, uzyskać jeszcze lepsze przybliżenie początkowe dla metody Newtona (lub podobnej).

Ponieważ zachodzi (12.2) z warunkiem początkowym $x(t^{*})=x^{*}$ , to przybliżoną wartość $x(t^{*}+h)$ możnaby uzyskać, stosując jakiś schemat różnicowy dla (12.2). Na przykład, korzystając dla (12.2) z jawnego schematu Eulera z krokiem $h$ , jako $x_{0}\approx x(t^{*}+h)$ położymy

$x_{0}=x(t^{*})+h\, x^{{\prime}}(t^{*})=x^{*}-h\cdot H_{{x}}(x^{*},t^{*})^{{-1}}H_{{t}}(x^{*},t^{*}).$

Ten sposób wyznaczania początkowego przybliżenia $x(t^{*}+h)$ nazywa się kontynuacją wzdłuż stycznej. Aby więc wyznaczyć $x_{0}$ , musimy rozwiązać układ równań z macierzą pochodnej $H_{{x}}(x^{*},t^{*})$ (wyznaczoną dla poprzednio znalezionego rozwiązania — to przecież macierz występująca w iteracji Newtona!) no i wyznaczyć wartość $H_{{t}}(x^{*},t^{*})$ — co zwykle nie jest zbyt trudne analitycznie (w przeciwnym przypadku, możemy zadowolić się, jak zwykle, różnicową aproksymacją).

Jeśli $x\in C^{2}(U)$ , to jakość tak uzyskanego przybliżenia jest znacznie wyższa niż w przypadku klasycznej metody kontynuacji. Rzeczywiście,

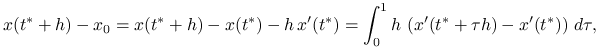$x(t^{*}+h)-x_{0}=x(t^{*}+h)-x(t^{*})-h\, x^{{\prime}}(t^{*})=\int _{0}^{1}h\,\left(x^{{\prime}}(t^{*}+\tau h)-x^{{\prime}}(t^{*})\right)\, d\tau,$

skąd, oznaczając $\tilde{l}=\max _{{t\in[t^{*},t^{*}+h]}}\| x^{{\prime\prime}}(t)\|$ , dostajemy na mocy lematu o wartości średniej oszacowanie

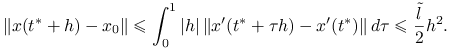$\| x(t^{*}+h)-x_{0}\|\leq\int _{0}^{1}|h|\,\| x^{{\prime}}(t^{*}+\tau h)-x^{{\prime}}(t^{*})\|\, d\tau\leq\dfrac{\tilde{l}}{2}h^{2}.$

Ćwiczenie 12.2

Dlaczego w metodzie kontynuacji wzdłuż stycznej, zastosowanie schematu niejawnego do rozwiązywania (12.2) nie miałoby większego sensu?

Rozwiązanie:

Bo, po pierwsze, wymagałoby rozwiązania podobnego równania nieliniowego, a po drugie — byłoby niepotrzebnie kosztowne. Przecież nas i tak interesuje tylko wykonanie jednego kroku takiego schematu!

W świetle powyższego, nabiera znaczenia kwestia doboru właściwej wielkości kroku kontynuacji $h$ . Na razie dysponujemy jedynie informacją jakościową, że ,,dla $h$ dostatecznie małego”, dostaniemy zbieżność. Jednak w praktyce chcielibyśmy używać rozsądnie małych (czytaj: nie za małych) $h$ — bo obniża to koszt wyznaczenia aproksymacji $x(t)$ dla $t\in U$ . Istnieją na szczęście strategie kontroli kroku kontynuacji $h$ [5], analogiczne jak w przypadku równań różniczkowych, ale dostosowane do tej konkretnej sytuacji: zagwarantowania (kwadratowej) zbieżności metody Newtona startującej z $x_{0}$ .

Warto także wiedzieć, że istnieją bardziej wyrafinowane techniki kontynuacji, które pozwalają przejść przez punkty krytyczne gałęzi (w których pochodna po $t$ jest nieokreślona)

12.2.2. Metoda homotopii

Jeśli trudno znaleźć dobry punkt startowy dla metody Newtona dla równania

$F(x)=0,$

możemy spróbować sztucznie wprowadzić parametr $t\in[0,1]$ i określić równanie (12.1) tak, by

$H(x,1)=F(x)$

oraz

$H(x,0)=\tilde{F}(x),$

przy czym dla $\tilde{F}$ jesteśmy w stanie łatwo wygenerować dobry punkt startowy. Jeśli tak, to postępując zgodnie z metodą kontynuacji — rozwiązując $H(x,t_{i})=0$ dla kolejnych wartości $t_{i}$ , poczynając od zera — dojdziemy w końcu do $t_{i}=1$ , i tym samym wygenerujemy dlań dobre przybliżenie startowe.

Taka metoda globalizacji zbieżności metody Newtona — przez wykorzystanie kontynuacji dla odpowiednio spreparowanej rodziny zadań z parametrem — nosi nazwę metody homotopii, gdyż w sposób ciągły przeprowadzamy zadanie ,,łatwe” na zadanie ,,trudne”. Należy jednak pamiętać, że w praktyce ta metoda może, ale nie musi się sprawdzić, gdyż znalezienie dobrej homotopii $H$ może być sprawą znacznie trudniejszą niż znalezienie dobrego $x_{0}$ ! Zazwyczaj ,,naturalne” pomysły na $H$ , np. wziąć ,,bardzo łatwą” $\tilde{F}(x)$ i określić