Zagadnienia
5. Proste metody iteracyjne rozwiązywania układów równań liniowych
Zajmiemy się przybliżonymi metodami rozwiązywania układów równań liniowych
z nieosobliwą rzeczywistą macierzą ![]() . Jak już sugerowaliśmy we wstępie, wraz z coraz większymi modelami pojawiającymi się w praktyce obliczeniowej,
częściej zachodzi potrzeba rozwiązywania zadań algebry liniowej o bardzo wielkiej liczbie niewiadomych.
Gdy
. Jak już sugerowaliśmy we wstępie, wraz z coraz większymi modelami pojawiającymi się w praktyce obliczeniowej,
częściej zachodzi potrzeba rozwiązywania zadań algebry liniowej o bardzo wielkiej liczbie niewiadomych.
Gdy ![]() jest dużego rozmiaru, metody bezpośrednie (wykorzystujące na przykład rozkład LU metodą eliminacji Gaussa lub inne rozkłady macierzy, np. QR) mogą być zbyt kosztowne lub mniej wygodne w użyciu. Przykładowo, jeśli niewiadomych jest kilka milionów, a macierz nie ma żadnej specjalnej struktury, to korzystając z eliminacji Gaussa musielibyśmy wykonać rzędu
jest dużego rozmiaru, metody bezpośrednie (wykorzystujące na przykład rozkład LU metodą eliminacji Gaussa lub inne rozkłady macierzy, np. QR) mogą być zbyt kosztowne lub mniej wygodne w użyciu. Przykładowo, jeśli niewiadomych jest kilka milionów, a macierz nie ma żadnej specjalnej struktury, to korzystając z eliminacji Gaussa musielibyśmy wykonać rzędu ![]() działań arytmetycznych (i zarezerwować rzędu
działań arytmetycznych (i zarezerwować rzędu ![]() bajtów — czyli
bajtów — czyli ![]() GB — pamięci na czynniki rozkładu). Zakładając optymistycznie, że nasz komputer jest w stanie wykonać
GB — pamięci na czynniki rozkładu). Zakładając optymistycznie, że nasz komputer jest w stanie wykonać ![]() działań na sekundę (czyli jest w stanie realnie osiągnąć wydajność 10 Gflopów/s), dawałoby to
działań na sekundę (czyli jest w stanie realnie osiągnąć wydajność 10 Gflopów/s), dawałoby to ![]() sekund, czyli około 32 lat… Rozsądną alternatywą może być wtedy rozwiązanie układu w sposób przybliżony, ale za to znacznie tańszy lub wygodniejszy. Jednym ze sposobów przybliżonego rozwiązywania układów równań liniowych są metody iteracyjne, szczególnie użyteczne wówczas, gdy
sekund, czyli około 32 lat… Rozsądną alternatywą może być wtedy rozwiązanie układu w sposób przybliżony, ale za to znacznie tańszy lub wygodniejszy. Jednym ze sposobów przybliżonego rozwiązywania układów równań liniowych są metody iteracyjne, szczególnie użyteczne wówczas, gdy ![]() jest macierzą rozrzedzoną.
jest macierzą rozrzedzoną.
5.1. Macierze rozrzedzone
Macierze, w których bardzo wiele elementów jest zerowych, nazywamy macierzami rozrzedzonymi lub, potocznie, rzadkimi. Dla odróżnienia, macierze, które nie są rzadkie, nazwiemy gęstymi — przykładem takiej macierzy jest macierz, której wszystkie elementy są niezerowe. Intuicyjnie możemy spodziewać się, że praktyczne zadania liniowe wielkiego wymiaru będą prowadziły właśnie do macierzy rozrzedzonej, gdyż związki pomiędzy niewiadomymi w pojedynczym równaniu zadanego układu nie będą raczej dotyczyć wszystkich, tylko wybranej (nielicznej) grupy innych niewiadomych.
Wykorzystanie rozrzedzenia macierzy nie tylko może doprowadzić do algorytmów istotnie szybszych od ich analogonów dla macierzy gęstych (jak pamiętamy, standardowe algorytmy oparte na rozkładzie macierzy gęstej, np. LU, potrzebują ![]() działań arytmetycznych), ale wręcz może być jedynym realnym sposobem na to, by niektóre zadania w ogóle
stały się rozwiązywalne przy obecnym stanie techniki obliczeniowej!
działań arytmetycznych), ale wręcz może być jedynym realnym sposobem na to, by niektóre zadania w ogóle
stały się rozwiązywalne przy obecnym stanie techniki obliczeniowej!
Gdy ![]() jest rozrzedzona, mnożenie takiej macierzy przez wektor jest bardzo tanie (koszt jest proporcjonalny do liczby niezerowych elementów macierzy).
Dlatego, konstruując metodę przybliżonego rozwiązywania układu, warto oprzeć się na iteracji, których głównym składnikiem jest operacja mnożenia przez
jest rozrzedzona, mnożenie takiej macierzy przez wektor jest bardzo tanie (koszt jest proporcjonalny do liczby niezerowych elementów macierzy).
Dlatego, konstruując metodę przybliżonego rozwiązywania układu, warto oprzeć się na iteracji, których głównym składnikiem jest operacja mnożenia przez ![]() lub jej część.
lub jej część.
5.1.1. Przykłady macierzy rozrzedzonych
Jak zobaczymy poniżej, rzeczywiście łatwo można spotkać realne zadania matematyki stosowanej, w których macierz wymiaru ![]() ma tylko
ma tylko ![]() niezerowych elementów. Omówimy tu dwie klasy takich zadań: dyskretyzacje równań różniczkowych oraz łańcuchy Markowa z dyskretną przestrzenią stanów.
niezerowych elementów. Omówimy tu dwie klasy takich zadań: dyskretyzacje równań różniczkowych oraz łańcuchy Markowa z dyskretną przestrzenią stanów.
Równania różniczkowe cząstkowe
Jednym ze szczególnie ważnych źródeł układów równań z macierzami rozrzedzonymi są równania różniczkowe cząstkowe (pochodzące np. z modeli pogody, naprężeń w konstrukcji samochodu, przenikania kosmetyków do głębszych warstw skóry, itp.).
Przykład 5.1 (Dyskretyzacja jednowymiarowego laplasjanu)
Rozważmy modelowe eliptyczne równanie różniczkowe z jednorodnym warunkiem brzegowym Dirichleta
| (5.1) | ||||
| (5.2) |
w którym ![]() jest szukanym rozwiązaniem, a
jest szukanym rozwiązaniem, a ![]() — zadaną funkcją. Aby znaleźć jego przybliżone rozwiązanie, możemy na przykład zastąpić równanie różniczkowe odpowiadającym mu równaniem różnicowym,
— zadaną funkcją. Aby znaleźć jego przybliżone rozwiązanie, możemy na przykład zastąpić równanie różniczkowe odpowiadającym mu równaniem różnicowym,
| (5.3) | ||||
| (5.4) |
gdzie ![]() ma odpowiadać wartości rozwiązania w węźle dyskretyzacji
ma odpowiadać wartości rozwiązania w węźle dyskretyzacji ![]() ,
, ![]() , oraz
, oraz ![]() , przy czym
, przy czym ![]() . Odpowiedzią na pytanie, jak dobrze (i czy w ogóle) takie rozwiązanie dyskretne aproksymuje rozwiązanie dokładne, zajmujemy się na wykładzie z Numerycznych równań różniczkowych; tutaj zobaczymy, do jakiego zagadnienia algebraicznego prowadzi równanie różnicowe (5.3).
. Odpowiedzią na pytanie, jak dobrze (i czy w ogóle) takie rozwiązanie dyskretne aproksymuje rozwiązanie dokładne, zajmujemy się na wykładzie z Numerycznych równań różniczkowych; tutaj zobaczymy, do jakiego zagadnienia algebraicznego prowadzi równanie różnicowe (5.3).
Jest to oczywiście równanie liniowe na współczynniki ![]() ,
,
gdzie
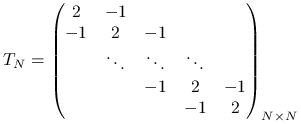 |
(5.5) |
oraz ![]() . Ponieważ interesują nas dobre przybliżenia (to znaczy przypadek, gdy
. Ponieważ interesują nas dobre przybliżenia (to znaczy przypadek, gdy ![]() jest bardzo małe), znaczy to, że
jest bardzo małe), znaczy to, że ![]() będzie bardzo duże. Nasza macierz jest rzeczywiście macierzą rozrzedzoną, bo ma nieco mniej niż
będzie bardzo duże. Nasza macierz jest rzeczywiście macierzą rozrzedzoną, bo ma nieco mniej niż ![]() niezerowych elementów. Jej współczynnik wypełnienia (ang. density), czyli stosunek liczby niezerowych do liczby wszystkich elementów macierzy, jest rzędu
niezerowych elementów. Jej współczynnik wypełnienia (ang. density), czyli stosunek liczby niezerowych do liczby wszystkich elementów macierzy, jest rzędu ![]() i maleje ze wzrostem
i maleje ze wzrostem ![]() .
.
Otrzymana powyżej macierz, aczkolwiek ma bardzo wiele cech charakterystycznych dla dyskretyzacji ,,poważniejszych” równań różniczkowych, wydaje się jednak zbyt trywialna, by traktować ją metodą inną niż eliminacja Gaussa (uwzględniając jej pasmową strukturę): rzeczywiście, jest to macierz trójdiagonalna (a przy tym: symetryczna i dodatnio określona), zatem właściwie zrealizowany algorytm eliminacji Gaussa (lub lepiej: rozkładu ![]() ) pozwoli nam wyznaczyć rozwiązanie układu
) pozwoli nam wyznaczyć rozwiązanie układu ![]() kosztem
kosztem ![]() , a więc — z dokładnością do stałej — optymalnym.
, a więc — z dokładnością do stałej — optymalnym.
Jednak, gdy przejdziemy do wyższych wymiarów i być może dodatkowo regularną siatkę węzłów dyskretyzacji zastąpimy na przykład nieregularną siatką elementu skończonego, uzyskamy macierze o znacznie bardziej skomplikowanej strukturze, które już nie tak łatwo poddają się eliminacji Gaussa.
Przykład 5.2 (Dyskretyzacja wielowymiarowego laplasjanu)
Przez analogię z poprzednim przykładem, rozważmy równanie Poissona w obszarze ![]() , z jednorodnym warunkiem Dirichleta:
, z jednorodnym warunkiem Dirichleta:
| (5.6) | ||||
| (5.7) |
w którym ![]() jest szukanym rozwiązaniem, a
jest szukanym rozwiązaniem, a ![]() — zadaną funkcją.
— zadaną funkcją. ![]() oznacza operator Laplace'a,
oznacza operator Laplace'a,
W dalszym ciągu przyjmiemy, dla ominięcia dodatkowych trudności, że ![]() jest kostką jednostkową:
jest kostką jednostkową: ![]() .
.
Aby znaleźć przybliżone rozwiązanie, znów możemy na przykład zastąpić równanie różniczkowe odpowiadającym mu równaniem różnicowym. Wybierzemy
tu najmniej efektywną, ale za to koncepcyjnie najprostszą metodę dyskretyzacji, opartą na równomiernej siatce węzłów w ![]() .
.
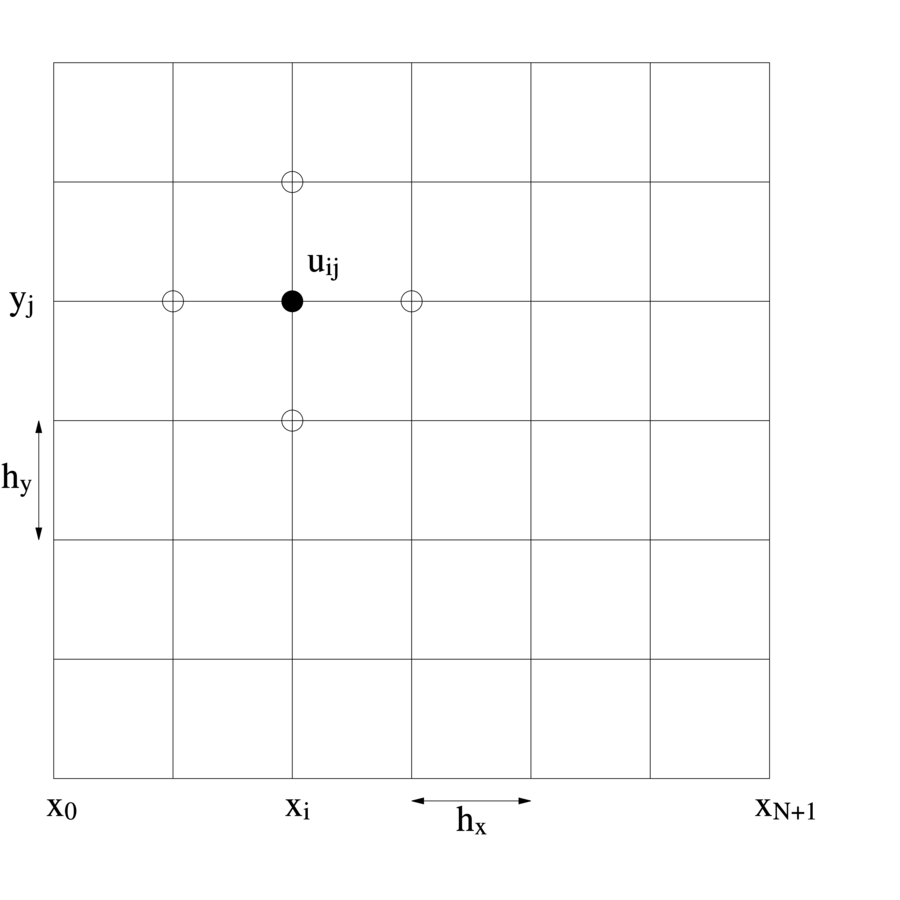
Przykładowo, jeśli ![]() , to weźmiemy siatkę węzłów
, to weźmiemy siatkę węzłów
![]() , gdzie
, gdzie ![]() , przy czym
, przy czym ![]() jest krokiem siatki w kierunku
jest krokiem siatki w kierunku ![]() i analogicznie
i analogicznie ![]() ,
zob. rysunek LABEL:regulargrid.pstex_t.
,
zob. rysunek LABEL:regulargrid.pstex_t.
Zastępując pochodne ilorazami różnicowymi [8]
| (5.8) |
dostajemy równanie różnicowe
| (5.9) |
W pozostałych węzłach siatki rozwiązanie przyjmuje wartość równą zero na mocy warunku brzegowego Dirichleta. Więcej na temat metod dyskretyzacji takich i podobnych równań różniczkowych można dowiedzieć się na wykładzie Numeryczne równania różniczkowe.
W dalszym ciągu, dla uproszczenia zapisu będziemy zakładać, że ![]() i w konsekwencji
i w konsekwencji ![]() . W takim układzie mamy do wyznaczenia
. W takim układzie mamy do wyznaczenia ![]() niewiadomych:
niewiadomych:
 |
które spełniają liniowy układ równań o postaci macierzowej
gdzie ![]() jest tym razem pięciodiagonalną macierzą o blokowej strukturze,
jest tym razem pięciodiagonalną macierzą o blokowej strukturze,
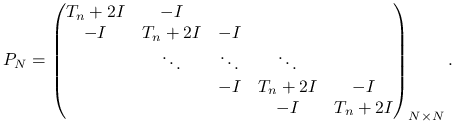 |
(5.10) |
W kolejnych diagonalnych blokach ![]() znajdują się macierze trójdiagonalne
znajdują się macierze trójdiagonalne ![]() , gdzie
, gdzie ![]() jest znaną już nam macierzą dyskretyzacji jednowymiarowego laplasjanu. Używając więc symbolu Kroneckera dla iloczynu tensorowego macierzy mamy przy naszej numeracji niewiadomych
jest znaną już nam macierzą dyskretyzacji jednowymiarowego laplasjanu. Używając więc symbolu Kroneckera dla iloczynu tensorowego macierzy mamy przy naszej numeracji niewiadomych
W przypadku tej macierzy, prosta strategia polegająca na eliminacji Gaussa (z wykorzystaniem dodatkowo faktu, że ![]() jest pasmowa, o szerokości pasma
jest pasmowa, o szerokości pasma ![]() ), dałaby nam szansę rozwiązać to równanie kosztem
), dałaby nam szansę rozwiązać to równanie kosztem ![]() , co jest, przy dużych wielkościach
, co jest, przy dużych wielkościach ![]() , wartością trudną do zaakceptowania.
, wartością trudną do zaakceptowania.
Prowadząc analogicznie dyskretyzację na jednorodnej siatce trójwymiarowego zadania Poissona na kostce jednostkowej (![]() ), dostalibyśmy
), dostalibyśmy ![]() oraz zadanie z macierzą siedmiodiagonalną (o szerokości pasma
oraz zadanie z macierzą siedmiodiagonalną (o szerokości pasma ![]() ):
):
| (5.11) |
Nawet dla średnich wartości ![]() , układ ten trudno rozwiązać metodą bezpośrednią, opartą na prostym rozkładzie pasmowej macierzy (tutaj na przykład: rozkładzie Cholesky'ego), zarówno ze względu na koszt obliczeniowy, jak i koszt pamięciowy. Rzeczywiście, koszt rozkładu Cholesky'ego uwzględniającego to, że w czynnikach rozkładu poza pasmem nie pojawią się elementy niezerowe wyniesie
, układ ten trudno rozwiązać metodą bezpośrednią, opartą na prostym rozkładzie pasmowej macierzy (tutaj na przykład: rozkładzie Cholesky'ego), zarówno ze względu na koszt obliczeniowy, jak i koszt pamięciowy. Rzeczywiście, koszt rozkładu Cholesky'ego uwzględniającego to, że w czynnikach rozkładu poza pasmem nie pojawią się elementy niezerowe wyniesie ![]() w przypadku dwuwymiarowego równania Poissona i
w przypadku dwuwymiarowego równania Poissona i ![]() w przypadku trójwymiarowego równania Poissona (dlaczego?). To oczywiście mniej niż pesymistyczne
w przypadku trójwymiarowego równania Poissona (dlaczego?). To oczywiście mniej niż pesymistyczne ![]() , ale gdy
, ale gdy ![]() jest duże, może być wystarczająco zachęcające do tego, by poszukać tańszych rozwiązań, dających sensowne rozwiązanie w sensownym czasie.
jest duże, może być wystarczająco zachęcające do tego, by poszukać tańszych rozwiązań, dających sensowne rozwiązanie w sensownym czasie.
Przykład 5.3 (ewolucyjne równanie dyfuzji)
Rozważmy równanie
Dla uproszczenia przyjmiemy, że ![]() jest kwadratem jednostkowym. Wprowadzając dyskretyzację tego równania po zmiennej przestrzennej jak poprzednio, a po zmiennej czasowej — niejawny schemat Eulera (patrz rozdział o schematach różnicowych Numerycznych równań różniczkowych), otrzymujemy, po uwzględnieniu warunku brzegowego, liniowy układ równań algebraicznych na przybliżenie
jest kwadratem jednostkowym. Wprowadzając dyskretyzację tego równania po zmiennej przestrzennej jak poprzednio, a po zmiennej czasowej — niejawny schemat Eulera (patrz rozdział o schematach różnicowych Numerycznych równań różniczkowych), otrzymujemy, po uwzględnieniu warunku brzegowego, liniowy układ równań algebraicznych na przybliżenie ![]() rozwiązania w chwili
rozwiązania w chwili ![]() ,
,
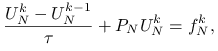 |
gdzie ![]() jest określone jak w poprzednim przykładzie oraz
jest określone jak w poprzednim przykładzie oraz
i węzły w ![]() numerujemy zgodnie z regułą podaną powyżej.
Grupując niewiadome po lewej stronie, dostajemy równanie
numerujemy zgodnie z regułą podaną powyżej.
Grupując niewiadome po lewej stronie, dostajemy równanie
a więc takie, w którym macierz układu jest dalej rozrzedzona, ale — dla dostatecznie małych ![]() — jest ,,małym zaburzeniem” macierzy jednostkowej.
— jest ,,małym zaburzeniem” macierzy jednostkowej.
Gdy siatka nie jest regularna1Zazwyczaj w zaawansowanych metodach dyskretyzacji równań różniczkowych stosuje się właśnie takie siatki, często — adaptacyjnie dopasowane do przebiegu rozwiązania., macierze dyskretyzacji także tracą regularną strukturę (w powyższych przykładach była ona odwzwierciedlona w tym, że niezerowe elementy macierzy układały się wzdłuż nielicznych diagonali). Macierze bez regularnej struktury są jeszcze trudniejsze dla metod bezpośrednich ze względu na rosnące kłopoty w uniknięciu wypełnienia czynników rozkładu macierzy.
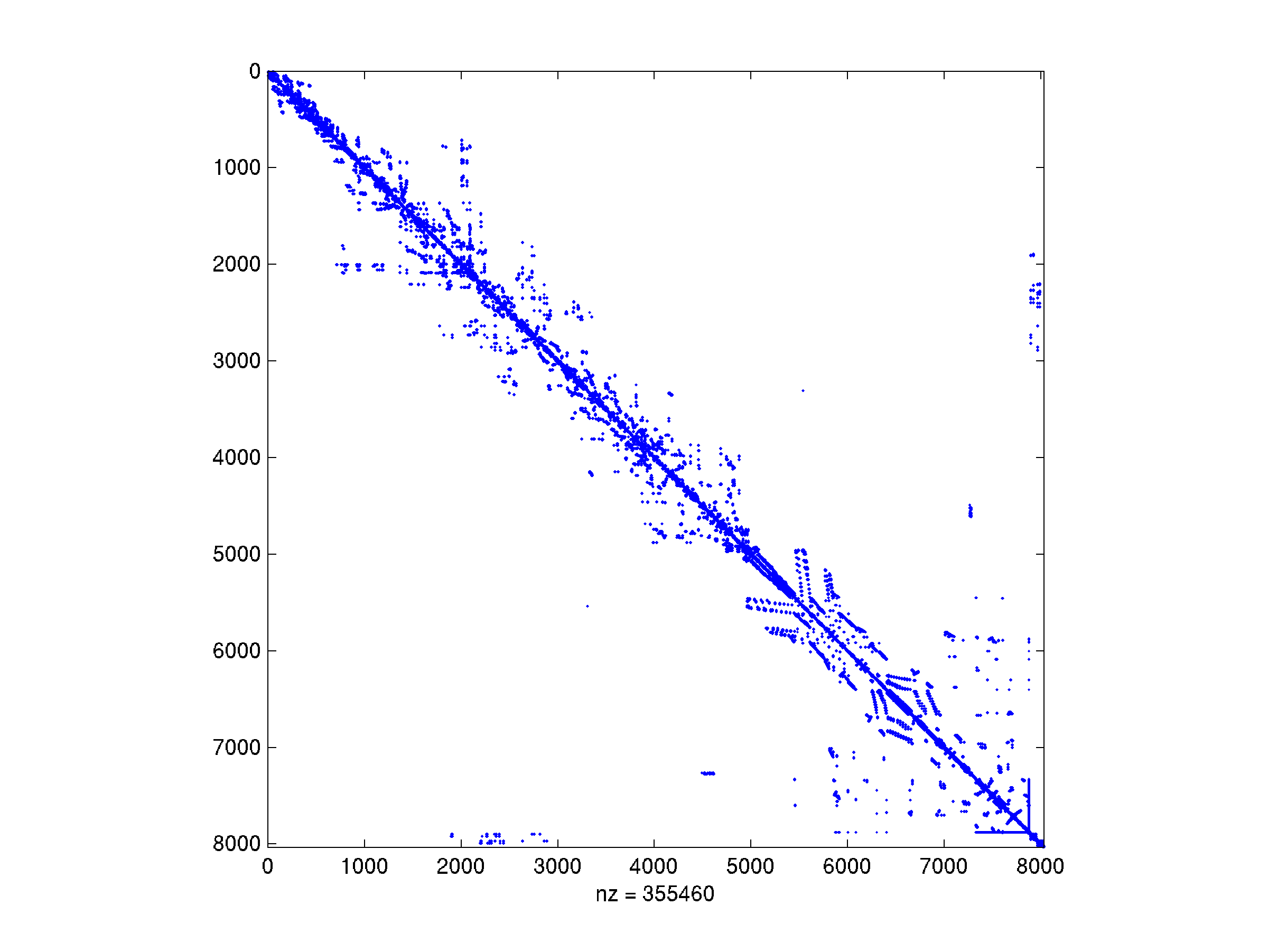
Przykład 5.4 (Macierz z kolekcji Boeinga)
Spójrzmy na macierz sztywności dla modelu silnika lotniczego, wygenerowaną swego czasu w zakładach Boeinga i pochodzącą z dyskretyzacji pewnego równania różniczkowego cząstkowego metodą elementu skończonego. Przykład pochodzi z kolekcji Tima Davisa. Jest to mała macierz, wymiaru 8032 (w kolekcji spotkasz równania z milionem i więcej niewiadomych).
Jej współczynnik wypełnienia (to znaczy, stosunek liczby niezerowych do wszystkich elementów macierzy) wynosi jedynie ![]() , a więc macierz jest bardzo rozrzedzona: w każdym wierszu są średnio tylko 44 niezerowe elementy.
, a więc macierz jest bardzo rozrzedzona: w każdym wierszu są średnio tylko 44 niezerowe elementy.
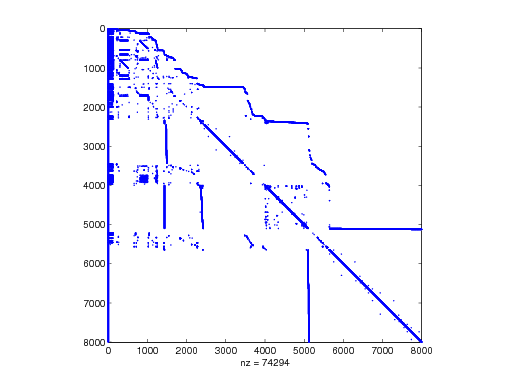
We wspomnianej kolekcji znajdzuje się jeszcze więcej macierzy rozrzedzonych, pochodzących z najrozmaitszych realnych modeli, nie tylko opartych na równaniach różniczkowych. Choć sporo z nich — tak jak tutaj przedstawiona — będzie symetrycznych, nie jest to regułą; inne układy równań ze zgromadzonego zbioru nie muszą mieć żadnej z pożądanych przez numeryka cech: regularnej/pasmowej struktury, symetrii, ani dodatniej określoności. Jedną z nich przedstawiamy poniżej.
Symulacje działania układów elektronicznych
Współczesne układy elektroniczne mogą zawierać miliony części (tranzystorów, rezystorów, kondensatorów), a ich projektowania jest procesem bardzo złożonym i kosztownym. Co więcej, w miarę postępów opracowywania, coraz trudniej o dokonanie w nich poważniejszych zmian projektu. Z tego powodu konieczna jest komputerowa symulacja ich działania. W ogólności prowadzi to do ogromnego układu równań różniczkowo–algebraicznych, ale także bada się modele (prawa Kirchhoffa!), sprowadzające się do rozwiązania układu równań liniowych wielkiego rozmiaru (![]() na poziomie kilku milionów).
na poziomie kilku milionów).

Wizualizacja grafu macierzy Circuit5M o rozmiarze powyżej pięciu milionów
(Źródło: The University of Florida Sparse Matrix Collection)Duże łańcuchy Markowa
Modele wielostanowych systemów kolejkowych (np. routera obsługującego wiele komputerów) także prowadzą do gigantycznych układów równań z macierzami rozrzedzonymi o specyficznej strukturze. Jeśli taki układ może z danego stanu przejść tylko do niewielu innych, macierz reprezentująca łańcuch Markowa będzie rozrzedzona.
Jednym z zadań, w którym rozważa się bodaj największy ,,naturalnie” pojawiający się łańcuch Markowa jest zadanie wyznaczania tzw. PageRank — wektora wartościującego strony internetowe w wyszukiwarce Google (zob. artykuł ,,Miara ważności” K. Diksa w Delcie 8/2008): macierz ta jest oryginalnie bardzo rozrzedzona, całkowicie nieregularna i niesymetryczna, a jej rozmiar jest równy liczbie indeksowanych stron WWW (a więc mniej więcej rzędu ![]() ).
).
Ćwiczenie 5.1
Wykaż, że zadanie ![]() można rozwiązać, korzystając z eleminacji Gaussa bez wyboru elementu głównego kosztem
można rozwiązać, korzystając z eleminacji Gaussa bez wyboru elementu głównego kosztem ![]() .
.
Ćwiczenie 5.2
Niech macierz ![]() będzie macierzą pasmową rozmiaru
będzie macierzą pasmową rozmiaru ![]() , o szerokości pasma
, o szerokości pasma ![]() :
:
Wykaż, że rozkład LU (bez wyboru elementu głównego) macierzy ![]() można wyznaczyć kosztem
można wyznaczyć kosztem ![]() działań arytmetycznych. Jak zmieni się odpowiedź, gdy trzeba będzie dokonać wyboru elementu głównego w kolumnie?
działań arytmetycznych. Jak zmieni się odpowiedź, gdy trzeba będzie dokonać wyboru elementu głównego w kolumnie?
Ćwiczenie 5.3
Zbadaj koszt rozkładu LU macierzy ![]() , w którym wykorzystuje się jedynie informację o tym, że
, w którym wykorzystuje się jedynie informację o tym, że ![]() jest macierzą pasmową.
jest macierzą pasmową.
Mamy ![]() i szerokość pasma jest równa
i szerokość pasma jest równa ![]() . Zatem na mocy poprzedniego zadania, koszt jest rzędu
. Zatem na mocy poprzedniego zadania, koszt jest rzędu ![]() .
.
5.2. Macierze rozrzedzone: implementacja
Zanim przystąpimy do omawiania metod rozwiązywania układów równań liniowych z macierzami rozrzedzonymi, warto zapoznać się ze sposobami reprezentacji (formatami) macierzy rozrzedzonych. Ponieważ macierze rozrzedzone mają dużo zerowych elementów, ogólną zasadą jest zapamiętywanie tylko tych różnych od zera, w połączeniu z informacją o ich lokalizacji w macierzy. Spośród wielu struktur danych wygodnych dla przechowywania macierzy rozrzedzonych, opisanych m.in. w monografii [13], największą popularnością wśród numeryków cieszą się dwa: format współrzędnych oraz format spakowanych kolumn (lub wierszy)2Mniej popularny format diagonalny spotkamy m.in. w reprezentacji macierzy pasmowych w LAPACKu.. Liczbę niezerowych elementów macierzy ![]() rozmiaru
rozmiaru ![]() będziemy oznaczali, przez analogię do funkcji MATLABa,
będziemy oznaczali, przez analogię do funkcji MATLABa, ![]() .
.
Format współrzędnych
Jest to najprostszy sposób reprezentacji macierzy rozrzedzonych. Do zapamiętania macierzy ![]() rozmiaru
rozmiaru ![]() , liczącej
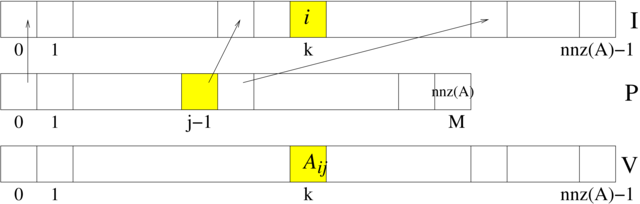
, liczącej ![]() niezerowych elementów, wykorzystujemy trzy wektory:
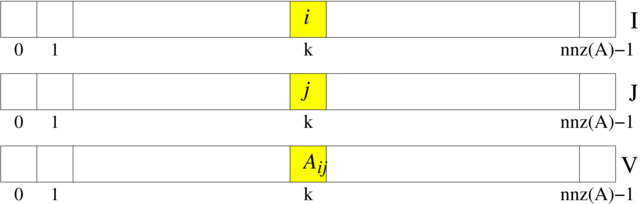
niezerowych elementów, wykorzystujemy trzy wektory: I,
J — oba typu int — oraz V, typu double,
wszystkie o długości ![]() , przy czym zachodzi
, przy czym zachodzi
zob. rysunek 5.4.
Przykład 5.5 (Macierz jednowymiarowego laplasjanu w formacie współrzędnych)
Zdefiniujemy niezbędne struktury danych i następnie wypełnimy je tak, by reprezentować macierz ![]() jednowymiarowego laplasjanu (5.5) w formacie współrzędnych. Macierz
jednowymiarowego laplasjanu (5.5) w formacie współrzędnych. Macierz ![]() jest kwadratowa rozmiaru
jest kwadratowa rozmiaru ![]() , o co
najwyżej
, o co
najwyżej ![]() niezerowych elementach.
niezerowych elementach.
Poniższa struktura:
typedef struct {
int I;
int J;
double V;
} SpElem;
będzie odpowiadała jednemu elementowi reprezentowanej macierzy. Cała macierz SpElem, na które przydzielamy miejsce:
SpElem *T; /* alokujemy miejsce na 3N elementów */ T = (SpElem *) calloc(3*N, sizeof(SpElem));
Zwróćmy uwagę na to, że do przydzielenia pamięci użyliśmy tym razem funkcji calloc(), a nie malloc(), jak zwykle. To dla większego bezpieczeństwa, bo calloc() wypełnia zerami przydzieloną pamięć.
Teraz możemy wypełnić tablicę. Jak widzimy z dalszego ciągu kodu, zmienną T_NNZ inkrementujemy od początkowej wartości ![]() za każdym razem, gdy do macierzy
za każdym razem, gdy do macierzy T zapisujemy kolejny element — w ten sposób będziemy dokładnie wiedzieli, ile w rzeczywistości (potencjalnie) niezerowych elementów wpisaliśmy do zaalokowanej tablicy.
int nnz = 0; /* bieżąca liczba wpisanych do tablicy elementów */
/* wypełniamy macierz */
for(i = 1; i <= N-1; i++)
{
/* element diagonalny */
T[nnz].I = i;
T[nnz].J = i;
T[nnz].V = 2;
nnz++;
/* element naddiagonalny w i-tym wierszu */
T[nnz].I = i;
T[nnz].J = i+1;
T[nnz].V = -1;
nnz++;
/* element poddiagonalny w i-tej kolumnie */
T[nnz].I = i+1;
T[nnz].J = i;
T[nnz].V = -1;
nnz++;
}
/* ostatni element, (N,N) */
T[nnz].I = N;
T[nnz].J = N;
T[nnz].V = 2;
nnz++;
Nie zawsze taka forma implementacji formatu współrzędnych będzie możliwa: często wybór implementacji będzie narzucony przez biblioteki, jakich zechcemy używać.
Format spakowanych kolumn (lub wierszy)
Format współrzędnych nie narzucał żadnego uporządkowania elementów macierzy — można było je umieszczać w dowolnej kolejności. Z drugiej strony, narzucenie sensownego porządku mogłoby wspomóc realizację wybranych istotnych operacji na macierzy, na przykład, aby wygodnie było realizować działanie (prawostronnego) mnożenia macierzy przez wektor, wygodnie byłoby przechowywać elementy macierzy wierszami. Tak właśnie jest zorganizowany format spakowanych wierszy (CSR, ang. Compressed Sparse Row). Analogicznie jest zdefiniowany format spakowanych kolumn (CSC, Compressed Sparse Column), którym zajmiemy się bliżej.
Podobnie jak w przypadku formatu współrzędnych, macierz w formacie CSC jest
przechowywana w postaci trzech wektorów. V jest wektorem typu
double o długości ![]() , zawierającym kolejne niezerowe elementy macierzy
, zawierającym kolejne niezerowe elementy macierzy ![]() wpisywane kolumnami,
wpisywane kolumnami, I jest wektorem typu int, także o długości ![]() , zawierającym numery wierszy macierzy
, zawierającym numery wierszy macierzy ![]() , odpowiadających elementom z
, odpowiadających elementom z V. Natomiast zamiast tablicy J, jak to było w
formacie współrzędnych, mamy krótszy wektor typu int, P, o
długości ![]() , zawierający na
, zawierający na ![]() miejscu indeks pozycji w
miejscu indeks pozycji w V, od
której w V rozpoczynają się elementy ![]() -tej kolumny macierzy
-tej kolumny macierzy ![]() (zob. rysunek 5.5).
(zob. rysunek 5.5).
W ten sposób, wartości kolejnych elementów ![]() -tej kolumny macierzy
-tej kolumny macierzy ![]() znajdują się w tablicy
znajdują się w tablicy V na pozycjach o indeksach P[j-1]…P[j]-1. Konsekwentnie, zawsze P[0]=0, a ostatni element, P[M], jest równy ![]() . Dzięki temu, takie operacje, jak na przykład wydobycie jednej kolumny z macierzy
. Dzięki temu, takie operacje, jak na przykład wydobycie jednej kolumny z macierzy ![]() , lub mnożenie przez wektor, są łatwiejsze do implementacji w schludnej, bezwariantowej pętli [13].
, lub mnożenie przez wektor, są łatwiejsze do implementacji w schludnej, bezwariantowej pętli [13].
Ostatecznie mamy więc zależność
Z tego rodzaju formatu reprezentacji macierzy rzadkich (z drobnymi modyfikacjami) korzystają np. pakiety Octave, MATLAB i UMFPACK.
Przykład 5.6 (Procedura mnożenia macierzy w formacie CSC przez wektor)
Mając macierz w formacie CSC, zadaną tablicami I[NNZ], P[M+1], V[NNZ], możemy napisać zgrabną procedurę mnożenia jej przez wektor x[M]. Wynik będziemy zapisywać w wektorze y[N]:
for(i = 0; i < N; i++) y[i] = 0.0; /* zerujemy wektor wynikowy */ for(j = 0; j < M; j++) for(k = P[j]; k < P[j+1]; k++) y[I[k]] += V[k]*x[j];
Ćwiczenie 5.4
Zapisz w pseudokodzie procedurę mnożenia macierzy rozrzedzonej przez wektor, gdy jest ona reprezentowana
w formacie współrzędnych,
w formacie CSR.
5.3. Metody stacjonarne rozwiązywania układów równań liniowych
Teraz zajmiemy się prostymi i historycznie najstarszymi metodami iteracyjnego rozwiązywania układu równań
gdzie nieosobliwa macierz ![]() jest (zapewne wielkiego) rozmiaru
jest (zapewne wielkiego) rozmiaru ![]() . Są one bodaj najprostsze w analizie i implementacji, ale — jak można się domyślić — w praktyce najmniej efektywne. Z drugiej strony, stanowią one ważny składnik jednej z najszybszych metod rozwiązywania niektórych trudnych układów równań (por. rozdział 8.3).
. Są one bodaj najprostsze w analizie i implementacji, ale — jak można się domyślić — w praktyce najmniej efektywne. Z drugiej strony, stanowią one ważny składnik jednej z najszybszych metod rozwiązywania niektórych trudnych układów równań (por. rozdział 8.3).
Rozważane przez nas w tym rozdziale metody opierają się na rozkładzie macierzy ![]() na część ,,łatwo odwracalną”,
na część ,,łatwo odwracalną”, ![]() , i ,,resztę”,
, i ,,resztę”, ![]() . Dokładniej,
równanie
. Dokładniej,
równanie ![]() można zapisać jako zadanie punktu stałego
można zapisać jako zadanie punktu stałego
a jeśli ![]() jest nieosobliwa, to równoważnie:
jest nieosobliwa, to równoważnie:
Ponieważ jest to zadanie znajdowania punktu stałego postaci ![]() , można spróbować zastosować doń metodę iteracji prostej Banacha:
, można spróbować zastosować doń metodę iteracji prostej Banacha:
| (5.12) |
Takie metody nazywamy stacjonarnymi metodami iteracyjnymi.
Ćwiczenie 5.5
Wykaż, że każdą stacjonarną metodę iteracyjną można zapisać w wygodniejszej (dlaczego?) do praktycznej implementacji postaci
gdzie ![]() .
.
Jest to wygodniejsza postać, bo wymaga operowania wektorem residuum ![]() , na którym zapewne będziemy opierać kryterium stopu iteracji (więc i tak wtedy byśmy go wyznaczali)). Nie wymaga też jawnego
, na którym zapewne będziemy opierać kryterium stopu iteracji (więc i tak wtedy byśmy go wyznaczali)). Nie wymaga też jawnego ![]() .
.
Metody stacjonarne można zapisać w ogólnej postaci
| (5.13) |
gdzie macierz ![]() oraz wektor
oraz wektor ![]() są tak dobrane, by punkt stały
są tak dobrane, by punkt stały ![]() równania (5.13) był rozwiązaniem równania wyjściowego
równania (5.13) był rozwiązaniem równania wyjściowego ![]() .
.
Dla stacjonarnej metody iteracyjnej, ![]() oraz
oraz ![]() . Macierz
. Macierz ![]() nazywamy macierzą iteracji, gdyż zachodzi
nazywamy macierzą iteracji, gdyż zachodzi
Jasne jest, że z twierdzenia Banacha o punkcie stałym wynika od razu następujący warunek zbieżności:
Stwierdzenie 5.1 (warunek wystarczający zbieżności metody stacjonarnej)
Jeśli ![]() , to metoda (5.13) jest zbieżna co najmniej liniowo do
, to metoda (5.13) jest zbieżna co najmniej liniowo do ![]() dla dowolnego
dla dowolnego ![]() . Tutaj
. Tutaj ![]() oznacza dowolną normę macierzową indukowaną przez normę wektorową.
oznacza dowolną normę macierzową indukowaną przez normę wektorową.
Dowód
Przy naszych założeniach, mamy do czynienia z kontrakcją ![]() , która odwzorowuje kulę
, która odwzorowuje kulę ![]() w siebie:
w siebie:
Ponieważ, z założenia, stała Lipschitza dla ![]() wynosi
wynosi ![]() , to z twierdzenia Banacha o kontrakcji (por. twierdzenie 9.1) wynika teza stwierdzenia.
, to z twierdzenia Banacha o kontrakcji (por. twierdzenie 9.1) wynika teza stwierdzenia.
Wniosek 5.1
Jeśli ![]() , to ciąg określony przez stacjonarną metodę iteracyjną jest zbieżny do
, to ciąg określony przez stacjonarną metodę iteracyjną jest zbieżny do ![]() oraz
oraz
Dowód
Aby stwierdzić zbieżność, wystarczy w poprzednim stwierdzeniu podstawić ![]() oraz
oraz ![]() . Oszacowanie błędu jest konsekwencją własności kontrakcji.
. Oszacowanie błędu jest konsekwencją własności kontrakcji.
Warunek konieczny i dostateczny zbieżności tej iteracji dla dowolnego wektora startowego ![]() podaje poniższe twierdzenie. Podkreślmy, że chodzi nam tu o zbieżność metody do rozwiązania układu, gdy startujemy z dowolnego przybliżenia początkowego
podaje poniższe twierdzenie. Podkreślmy, że chodzi nam tu o zbieżność metody do rozwiązania układu, gdy startujemy z dowolnego przybliżenia początkowego ![]() .
.
Twierdzenie 5.1 (warunek konieczny i dostateczny zbieżności metody stacjonarnej)
Niech ![]() będzie macierzą iteracji metody (5.13). Ciąg
będzie macierzą iteracji metody (5.13). Ciąg ![]() określony tą metodą jest zbieżny do rozwiązania
określony tą metodą jest zbieżny do rozwiązania ![]() dla dowolnego
dla dowolnego ![]() wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
Dowód
Na mocy (5.13) otrzymujemy równanie błędu ![]() ,
,
Konieczność warunku jest oczywista: jeśli metoda jest zbieżna dla każdego ![]() , to w szczególności dla takiego, że
, to w szczególności dla takiego, że ![]() jest równe wektorowi własnemu macierzy
jest równe wektorowi własnemu macierzy ![]() odpowiadającego zadanej (dowolnej) wartości własnej
odpowiadającego zadanej (dowolnej) wartości własnej ![]() . W konsekwencji,
. W konsekwencji,
a to oznacza, że ![]() .
.
To, że warunek wymieniany w tezie twierdzenia jest także wystarczający dla zbieżności metody, wynika z faktu (zob. [11]), że dla dowolnego ![]() istnieje norma macierzowa indukowana przez normę wektorową
istnieje norma macierzowa indukowana przez normę wektorową ![]() taka, że
taka, że
Skoro więc z założenia ![]() , to można dobrać takie
, to można dobrać takie ![]() , by
, by ![]() i w konsekwencji
i w konsekwencji
skąd ![]() .
.
Ćwiczenie 5.6
W powyższym dowodzie, jeśli ![]() jest zespolona, to odpowiadający jej wektor własny też jest zespolony, a więc — formalnie — nie może być uznany za kontrprzykład zbieżności, bo ta ma być ,,dla każdego
jest zespolona, to odpowiadający jej wektor własny też jest zespolony, a więc — formalnie — nie może być uznany za kontrprzykład zbieżności, bo ta ma być ,,dla każdego ![]() ”, a nie — ,,dla każdego
”, a nie — ,,dla każdego ![]() ”. Uzupełnij tę lukę pokazując, że jeśli nawet jeśli
”. Uzupełnij tę lukę pokazując, że jeśli nawet jeśli ![]() jest zespolona, to gdy
jest zespolona, to gdy ![]() można wskazać taki rzeczywisty wektor
można wskazać taki rzeczywisty wektor ![]() , że zbieżność nie będzie zachodzić.
, że zbieżność nie będzie zachodzić.
Zaletą stacjonarnych metod iteracyjnych jest ich prostota powodująca, że są one wyjątkow wdzięczne do szybkiego zaprogramowania. Zobaczymy to na przykładzie kilku klasycznych metod stacjonarnych: Jacobiego, Gaussa–Seidela i SOR. Wszystkie będą bazować na podziale macierzy ![]() na trzy części: diagonalną, ściśle dolną trójkątną i ściśle górną trójkątną:
na trzy części: diagonalną, ściśle dolną trójkątną i ściśle górną trójkątną:
| (5.14) |
gdzie
 |
5.3.1. Metoda Jacobiego
Biorąc w (5.12) ![]() , gdzie
, gdzie ![]() jest macierzą diagonalną składającą się
z wyrazów stojących na głównej przekątnej macierzy
jest macierzą diagonalną składającą się
z wyrazów stojących na głównej przekątnej macierzy
![]() (zob. (5.14)), otrzymujemy (o ile na przekątnej macierzy
(zob. (5.14)), otrzymujemy (o ile na przekątnej macierzy ![]() nie mamy zera) metodę iteracyjną
nie mamy zera) metodę iteracyjną
zwaną metodą Jacobiego.
Rozpisując ją po współrzędnych, dostajemy układ rozszczepionych równań (numer iteracji wyjątkowo zaznaczamy w postaci górnego indeksu):
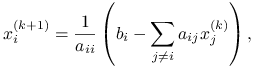 |
co znaczy dokładnie tyle, że w ![]() -tym równaniu wyjściowego układu przyjmujemy za współrzędne
-tym równaniu wyjściowego układu przyjmujemy za współrzędne ![]() wartości z poprzedniej iteracji i na tej podstawie wyznaczamy wartość
wartości z poprzedniej iteracji i na tej podstawie wyznaczamy wartość ![]() .
.
Widzimy więc, że metoda rzeczywiście jest banalna w implementacji, a dodatkowo jest w pełni równoległa: każdą współrzędną nowego przybliżenia możemy wyznaczyć niezależnie od pozostałych.
Twierdzenie 5.2 (O zbieżności metody Jacobiego)
W metodzie Jacobiego warunek dostateczny zbieżności,
![]() , jest spełniony np. wtedy, gdy macierz
, jest spełniony np. wtedy, gdy macierz ![]() ma
dominującą przekątną, tzn. gdy
ma
dominującą przekątną, tzn. gdy
| (5.15) |
Dowód
Rzeczywiście, ponieważ wyraz ![]() macierzy
macierzy ![]() wynosi
wynosi ![]() dla
dla ![]() oraz
oraz ![]() dla
dla ![]() , to
, to
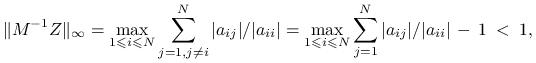 |
przy czym ostatnia nierówność wynika z warunku diagonalnej dominacji.
∎Niestety, w wielu ważnych wypadkach metoda Jacobiego, choć zbieżna, będzie zbieżna zbyt wolno, by nas zadowolić.
Przykład 5.7 (Macierz laplasjanu)
Macierz ![]() , zwana macierzą jednowymiarowego laplasjanu
, zwana macierzą jednowymiarowego laplasjanu
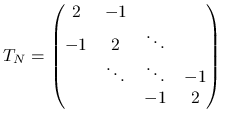 |
pojawia się w bardzo wielu zastosowaniach (patrz przykład 5.1), również jako sztucznie wprowadzane podzadanie w niektórych algorytmach
numerycznych. Ta macierz jest macierzą taśmową, symetryczną i dodatnio
określoną, więc układ równań z tą macierzą można bez trudu rozwiązać metodami
bezpośrednimi, kosztem ![]() . Jak jednak za chwilę się przekonamy, układ równań z macierzą
. Jak jednak za chwilę się przekonamy, układ równań z macierzą ![]() będzie wyjątkowo trudny dla klasycznej metody stacjonarnej.
będzie wyjątkowo trudny dla klasycznej metody stacjonarnej.
Stosując do ![]() metodę Jacobiego mamy
metodę Jacobiego mamy ![]() oraz
oraz ![]() . Obliczając
normę macierzy iteracji Jacobiego dostajemy
. Obliczając
normę macierzy iteracji Jacobiego dostajemy ![]() , co — jak wiemy z twierdzenia 5.1 — nie rozstrzyga jeszcze o jej zbieżności lub niezbieżności, ale już może stanowić dla nas poważne ostrzeżenie.
, co — jak wiemy z twierdzenia 5.1 — nie rozstrzyga jeszcze o jej zbieżności lub niezbieżności, ale już może stanowić dla nas poważne ostrzeżenie.
Potrzebna będzie bardziej subtelna analiza. Okazuje się, że są znane wzory na wartości własne ![]() macierzy
macierzy ![]() (por. ćwiczenie 5.8):
(por. ćwiczenie 5.8):
(a więc, ![]() ) dla
) dla ![]() W konsekwencji, wartościami własnymi
W konsekwencji, wartościami własnymi ![]() są liczby
są liczby ![]() . Ponieważ
. Ponieważ ![]() , znaczy to, że metoda Jacobiego jest zbieżna dla macierzy
, znaczy to, że metoda Jacobiego jest zbieżna dla macierzy ![]() .
.
Z drugiej strony, nie dajmy się zwieść optymizmowi matematyka (,,nie martw się, jest zbieżny…”): nietrudno sprawdzić, że ![]() , co oznacza, że metoda Jacobiego — choć zbieżna! — dla dużych
, co oznacza, że metoda Jacobiego — choć zbieżna! — dla dużych ![]() staje się
zbieżna tak wolno, że w praktyce bezużyteczna: na przykład, gdy
staje się
zbieżna tak wolno, że w praktyce bezużyteczna: na przykład, gdy ![]() ,
, ![]() , zatem potrzebowalibyśmy około 4600 iteracji, by mieć pewność, że początkowy błąd zredukowaliśmy zaledwie… 10 razy.
, zatem potrzebowalibyśmy około 4600 iteracji, by mieć pewność, że początkowy błąd zredukowaliśmy zaledwie… 10 razy.
Dopiero w rozdziale 8.3 przekonamy się, jak — przez niebanalne wykorzystanie głębszych informacji o samym zadaniu — można wykorzystać metodę stacjonarną do konstrukcji metody iteracyjnej o optymalnym koszcie, którą będziemy mogli stosować także do macierzy dwu- i trójwymiarowego laplasjanu.
Ćwiczenie 5.7
Wykaż, że wartości własne macierzy dwuwymiarowego laplasjanu ![]() — zob. (5.10) — są postaci
— zob. (5.10) — są postaci
dla ![]() Podobnie pokaż, że, wartości własne macierzy trójwymiarowego laplasjanu
Podobnie pokaż, że, wartości własne macierzy trójwymiarowego laplasjanu ![]() — zob. (5.11) — są postaci
— zob. (5.11) — są postaci
dla ![]()
Niech ![]() będzie rozkładem macierzy jednowymiarowego laplasjanu takim, że
będzie rozkładem macierzy jednowymiarowego laplasjanu takim, że ![]() jest macierzą diagonalną zawierającą wartości własne, a
jest macierzą diagonalną zawierającą wartości własne, a ![]() taka, że
taka, że ![]() zawiera wektory własne
zawiera wektory własne ![]() . Ponieważ macierz
. Ponieważ macierz ![]() to konsekwentnie
to konsekwentnie
Stąd wynika teza. Analogicznie postępujemy dla macierzy trójwymiarowego laplasjanu.
Ćwiczenie 5.8
Wykaż, że jeśli ![]() oraz
oraz ![]() , to rzeczywista trójdiagonalna macierz Toeplitza3Macierzą Toeplitza nazywamy macierz o stałych współczynnikach na diagonalach.
, to rzeczywista trójdiagonalna macierz Toeplitza3Macierzą Toeplitza nazywamy macierz o stałych współczynnikach na diagonalach.
 |
(5.16) |
ma jednokrotne wartości własne, równe
| (5.17) |
gdzie
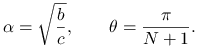 |
Zwróć uwagę na to, że gdy ![]() , wartości własne są zespolone.
Wektor własny
, wartości własne są zespolone.
Wektor własny ![]() macierzy
macierzy ![]() odpowiadający
odpowiadający ![]() ma współrzędne dane wzorem
ma współrzędne dane wzorem
| (5.18) |
Dla ![]() zachodzi
zachodzi
gdzie
 |
Znaczy to, że ![]() jest podobna do macierzy
jest podobna do macierzy ![]() — a więc ma te same wartości własne. Nietrudno sprawdzić wprost (ze wzorów trygonometrycznych), że
— a więc ma te same wartości własne. Nietrudno sprawdzić wprost (ze wzorów trygonometrycznych), że ![]() ma wektory i wartości własne takie, jak przewiduje wzór.
ma wektory i wartości własne takie, jak przewiduje wzór.
Przykład 5.8
Niech ![]() będzie losową kwadratową macierzą
będzie losową kwadratową macierzą ![]() , która ma średnio
, która ma średnio ![]() elementów w wierszu (zatem jej współczynnik wypełnienia wynosi
elementów w wierszu (zatem jej współczynnik wypełnienia wynosi ![]() ) i niech
) i niech
Dobierając do ![]() wartość
wartość ![]() możemy sterować stopniem diagonalnej dominacji macierzy
możemy sterować stopniem diagonalnej dominacji macierzy ![]() i, ostatecznie, zagwarantować sobie, że
i, ostatecznie, zagwarantować sobie, że ![]() jest diagonalnie dominująca.
jest diagonalnie dominująca.
W poniższym eksperymencie komputerowym możemy naocznie przekonać się, jak stopień dominacji diagonali wpływa na szybkość zbieżności metody Jacobiego. Dla porównania zobaczymy, jak z naszą macierzą radzi sobie metoda bezpośrednia: oparta na rozkładzie LU macierzy ![]() i starająca się wykorzystać w inteligentny sposób jej rozrzedzenie.
i starająca się wykorzystać w inteligentny sposób jej rozrzedzenie.
Ćwiczenie 5.9
Przekonaj się, czy stopień diagonalnej dominacji (wartość parametru p w skrypcie) ma istotny wpływ na szybkość zbieżności.
Domyślnie testy prowadzimy dla macierzy rozmiaru 2500. Sprawdź, jak zmieni się czas wykonania skryptu, gdy
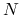 będzie jeszcze większe: która metoda: iteracyjna, czy bezpośrednia zagwarantuje nam sensowny wynik w krótszym czasie?
będzie jeszcze większe: która metoda: iteracyjna, czy bezpośrednia zagwarantuje nam sensowny wynik w krótszym czasie?Przekonaj się, że gdy rozmiar macierzy jest niewielki, na przykład
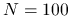 , nie ma większego sensu stosować metody iteracyjnej. Przy jakim poziomie tolerancji tol metoda iteracyjna staje się konkurencyjna dla bezpośredniej (pod względem czasu działania)?
, nie ma większego sensu stosować metody iteracyjnej. Przy jakim poziomie tolerancji tol metoda iteracyjna staje się konkurencyjna dla bezpośredniej (pod względem czasu działania)?
Ćwiczenie 5.10
Uzupełnij powyższy skrypt o wyznaczenie teoretycznej wartości współczynnika redukcji błędu w normie
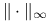 i porównaj ją z faktyczną szybkością redukcji błędu.
i porównaj ją z faktyczną szybkością redukcji błędu.Sprawdź, że symetria
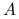 nie ma większego wpływu na szybkość zbieżności.
nie ma większego wpływu na szybkość zbieżności.
Przykład 5.9
Zdarzają się macierze — niestety, nie są to sztucznie generowane, akademickie przypadki — które są patologicznie trudne dla stacjonarnej metody iteracyjnej, a bardzo łatwe dla metody bezpośredniej. Jedną taką macierz już znamy: jest to macierz jednowymiarowego laplasjanu ![]() .
.
W naszym teście, dla zadania z macierzą ![]() i różnych wartości parametru
i różnych wartości parametru ![]() zbadamy szybkość zbieżności metody Jacobiego i porównamy czas jej działania z metodą bezpośrednią (w przypadku macierzy trójdiagonalnej jest ona praktycznie optymalna).
zbadamy szybkość zbieżności metody Jacobiego i porównamy czas jej działania z metodą bezpośrednią (w przypadku macierzy trójdiagonalnej jest ona praktycznie optymalna).
Tym razem zmiana ![]() wyraźnie wpływa na szybkość zbieżności, a dla
wyraźnie wpływa na szybkość zbieżności, a dla ![]() zbieżność jest — jak już zdążyliśmy się przekonać także analitycznie — jest bardzo wolna.
zbieżność jest — jak już zdążyliśmy się przekonać także analitycznie — jest bardzo wolna.
Ćwiczenie 5.11
Wyjaśnij przyczynę szybkiej zbieżności metody dla dużych
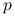 .
.
Domyślnie eksperymenty prowadzimy dla macierzy rozmiaru 25. Sprawdź, jak zmieni się czas wykonania skryptu, gdy
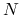 będzie większe: która metoda zagwarantuje nam wynik w krótszym czasie? Jak odpowiedź zależy od
będzie większe: która metoda zagwarantuje nam wynik w krótszym czasie? Jak odpowiedź zależy od 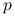 ?
?Jeśli zależałoby nam na obliczeniu dokładnego rozwiązania układu, powinniśmy znacząco zmniejszyć warunek stopu metody, tol, na przykład do poziomu
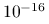 . Jak teraz wypada porównanie metody Jacobiego i bezpośredniej, gdy
. Jak teraz wypada porównanie metody Jacobiego i bezpośredniej, gdy 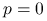 ?
?
Ćwiczenie 5.12
Rozważmy macierz
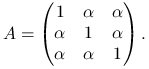 |
Wykaż, że
 ,
,metoda Jacobiego dla tej macierzy jest zbieżna, wtedy i tylko wtedy, gdy
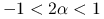 .
.
Czy rezultat o zbieżności metody Jacobiego można uogólnić na przypadek, gdy ![]() rozmiaru
rozmiaru ![]() ma na diagonali same jedynki, a poza nią wszystkie jej elementy są równe
ma na diagonali same jedynki, a poza nią wszystkie jej elementy są równe ![]() ?
?
5.3.2. Metoda Gaussa–Seidela
Heurystyka tej metody
opiera się na zmodyfikowaniu metody Jacobiego tak, by w każdym momencie iteracji korzystać z najbardziej ,,aktualnych” współrzędnych przybliżenia rozwiązania ![]() . Rzeczywiście, przecież wykonując jeden krok metody Jacobiego, czyli rozwiązując kolejno równania skalarne względem
. Rzeczywiście, przecież wykonując jeden krok metody Jacobiego, czyli rozwiązując kolejno równania skalarne względem ![]() dla
dla ![]() :
:
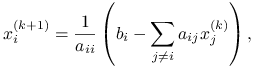 |
nietrudno zauważyć, że w części sumy, dla ![]() , moglibyśmy odwoływać się — zamiast do ,,starych”
, moglibyśmy odwoływać się — zamiast do ,,starych” ![]() — do ,,dokładniejszych”, świeżo wyznaczonych, wartości
— do ,,dokładniejszych”, świeżo wyznaczonych, wartości ![]() , tzn. ostatecznie wyznaczać
, tzn. ostatecznie wyznaczać
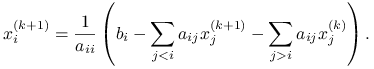 |
W języku rozkładu macierzy ![]() i iteracji
i iteracji ![]() mielibyśmy więc
mielibyśmy więc ![]() (dolny trójkąt macierzy
(dolny trójkąt macierzy ![]() z diagonalą) oraz
z diagonalą) oraz ![]() (ściśle górny trójkąt
(ściśle górny trójkąt ![]() ) i konsekwentnie zapis macierzowy iteracji
) i konsekwentnie zapis macierzowy iteracji
Twierdzenie 5.3 (O zbieżności metody Gaussa–Seidela)
Jeśli macierz ![]() jest diagonalnie dominująca, to metoda Gaussa–Seidela jest zbieżna do
jest diagonalnie dominująca, to metoda Gaussa–Seidela jest zbieżna do ![]() dla dowolnego wektora startowego
dla dowolnego wektora startowego ![]() .
.
Inny wariant tej metody dostalibyśmy, biorąc za ![]() górny trójkąt macierzy
górny trójkąt macierzy ![]() .
.
Uwaga 5.1
Obie metody, Jacobiego i (zwłaszcza) Gaussa–Seidela stosuje się także czasem w prostych algorytmach rozwiązywania układów równań nieliniowych: ich zaletą jest to, że głównym składnikiem iteracji jest rozwiązywanie skalarnego równania nieliniowego na każdym kroku metody.
Metoda Gaussa–Seidela jest w wielu przypadkach rzeczywiście szybciej zbieżna od metody Jacobiego, np. tak jest w przypadku macierzy jednowymiarowego laplasjanu, patrz wniosek 5.2. Wciąż jednak, dodajmy, dla tego zadania jej zbieżność jest zbyt wolna, by ją stosować jako samodzielną metodę.
Przykład 5.10
Kontynuując przykład 5.8, porównamy szybkość zbieżności metody Gaussa–Seidela i Jacobiego na tym samym zadaniu.
Ćwiczenie 5.13
Porównaj szybkość zbieżności metod Jacobiego i Gaussa–Seidela na macierzy ![]() jednowymiarowego laplasjanu.
jednowymiarowego laplasjanu.
Możesz przeprowadzić porównanie, prowadząc dobrze zaplanowane eksperymenty numeryczne. W MATLABie łatwo utworzysz macierz ![]() poleceniem
poleceniem
e = ones(N,1); TN = spdiags([-e, 2*e, -e], [-1,0,1], N, N);Jeśli interesuje Cię wynik teoretyczny, czytaj dalej.
5.3.3. Metoda SOR
Zbieżność metody Gaussa–Seidela można przyspieszyć, wprowadzając parametr relaksacji ![]() i kolejne współrzędne nowego przybliżenia
i kolejne współrzędne nowego przybliżenia ![]() wyznaczać, kombinując ze sobą poprzednie przybliżenie
wyznaczać, kombinując ze sobą poprzednie przybliżenie ![]() oraz współrzędną nowego przybliżenia
oraz współrzędną nowego przybliżenia ![]() , uzyskanego metodą Gaussa–Seidela:
, uzyskanego metodą Gaussa–Seidela:
Gdyby ![]() , dostalibyśmy z powrotem metodę Gaussa–Seidela. Ponieważ zwykle wybiera się
, dostalibyśmy z powrotem metodę Gaussa–Seidela. Ponieważ zwykle wybiera się ![]() , powstałą metodę nazywa się metodą nadrelaksacji (ang. successive overrelaxation, SOR), która jest na swój sposób szczytowym osiągnięciem wśród metod stacjonarnych.
Rozkład macierzy
, powstałą metodę nazywa się metodą nadrelaksacji (ang. successive overrelaxation, SOR), która jest na swój sposób szczytowym osiągnięciem wśród metod stacjonarnych.
Rozkład macierzy ![]() odpowiadający metodzie SOR z parametrem
odpowiadający metodzie SOR z parametrem ![]() jest zadany przez
jest zadany przez
Twierdzenie 5.4 (lemat Kahana o dopuszczalnych wartościach parametru relaksacji SOR)
Jeśli ![]() ma niezerową diagonalę, a metoda SOR jest zbieżna, to musi być
ma niezerową diagonalę, a metoda SOR jest zbieżna, to musi być ![]() .
.
Dowód
Wystarczy zbadać promień spektralny macierzy iteracji metody SOR, która jest równa ![]() .
Ponieważ macierz
.
Ponieważ macierz ![]() jest macierzą trójkątną o diagonali
jest macierzą trójkątną o diagonali ![]() , to
, to ![]() i w konsekwencji
i w konsekwencji
Ze względu na to, że wyznacznik macierzy jest równy produktowi jej wartości własnych, dochodzimy do wniosku, że ![]() , co kończy dowód.
, co kończy dowód.
Jako ciekawostkę odnotujmy poniższe
Twierdzenie 5.5 (Ostrowskiego i Reicha)
Jeśli ![]() , to SOR jest zbieżna dla dowolnego
, to SOR jest zbieżna dla dowolnego ![]() .
.
Dowód tego twierdzenia można znaleźć na przykład w [15, rozdział 8.3].
Dla klasy macierzy obejmującej niektóre spotykane w praktycznych zastosowaniach, można wskazać brzemienny w konsekwencje związek promienia spektralnego macierzy iteracji metody SOR i metody Jacobiego.
Definicja 5.1
Rzeczywistą macierz kwadratową ![]() rozmiaru
rozmiaru ![]() , o niezerowych elementach na diagonali, nazywamy macierzą zgodnie uporządkowaną, jeśli wartości własne macierzy
, o niezerowych elementach na diagonali, nazywamy macierzą zgodnie uporządkowaną, jeśli wartości własne macierzy
gdzie ![]() ,
, ![]() , są niezależne od
, są niezależne od ![]() .
.
Zauważmy, że ![]() jest macierzą iteracji metody Jacobiego dla macierzy
jest macierzą iteracji metody Jacobiego dla macierzy ![]() .
.
Szczególnym przypadkiem macierzy zgodnie uporządkowanych są macierze postaci
| (5.19) |
w których ![]() są nieosobliwymi macierzami diagonalnymi.
są nieosobliwymi macierzami diagonalnymi.
Rzeczywiście, dla macierzy postaci (5.19) mamy
gdzie
i w konsekwencji
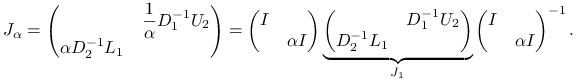 |
Zatem macierz ![]() jest podobna do
jest podobna do ![]() i w konsekwencji ma te same wartości własne, co
i w konsekwencji ma te same wartości własne, co ![]() (niezależnie od
(niezależnie od ![]() ), a więc — jest zgodnie uporządkowana.
), a więc — jest zgodnie uporządkowana.
Ćwiczenie 5.14
Wykaż, że jeśli ![]() jest macierzą trójdiagonalną (taką, jak na przykład
jest macierzą trójdiagonalną (taką, jak na przykład ![]() ) lub blokowo trójdiagonalną (taką, jak na przykład
) lub blokowo trójdiagonalną (taką, jak na przykład ![]() ) to
) to ![]() można poddać takiej permutacji
można poddać takiej permutacji ![]() wierszy i kolumn, że uzyskana macierz
wierszy i kolumn, że uzyskana macierz ![]() jest postaci (5.19)4W rzeczywistości, można wykazać więcej, że nawet bez tej permutacji macierze
jest postaci (5.19)4W rzeczywistości, można wykazać więcej, że nawet bez tej permutacji macierze ![]() i
i ![]() są zgodnie uporządkowane..
są zgodnie uporządkowane..
Rzeczywiście, w przypadku macierzy trójdiagonalnej ![]() wystarczy wziąć najpierw zmienne o indeksach nieparzystych, a potem — o indeksach parzystych:
wystarczy wziąć najpierw zmienne o indeksach nieparzystych, a potem — o indeksach parzystych:
![]() . Dla macierzy
. Dla macierzy ![]() wybieramy podobnie (tzw. red-black ordering).
wybieramy podobnie (tzw. red-black ordering).
Twierdzenie 5.6 (Vargi o związku pomiędzy zbieżnością SOR i metody Jacobiego)
Niech ![]() będzie macierzą zgodnie uporządkowaną i niech
będzie macierzą zgodnie uporządkowaną i niech ![]() . Wtedy jeśli
. Wtedy jeśli ![]() jest wartością własną macierzy iteracji metody Jacobiego, to
jest wartością własną macierzy iteracji metody Jacobiego, to ![]() też nią jest. Ponadto, jeśli
też nią jest. Ponadto, jeśli ![]() jest różną od zera wartością własną macierzy iteracji metody SOR z parametrem relaksacji
jest różną od zera wartością własną macierzy iteracji metody SOR z parametrem relaksacji ![]() oraz zachodzi
oraz zachodzi
to ![]() jest wartością własną macierzy iteracji Jacobiego. Na odwrót, jeśli
jest wartością własną macierzy iteracji Jacobiego. Na odwrót, jeśli ![]() jest wartością własną macierzy iteracji Jacobiego, to
jest wartością własną macierzy iteracji Jacobiego, to ![]() zadane powyższym wzorem jest wartością własną macierzy iteracji SOR.
zadane powyższym wzorem jest wartością własną macierzy iteracji SOR.
Dowód
Macierz iteracji metody Jacobiego to po prostu
(ostatnia równość na mocy założenia). Stąd oczywiście wynika część pierwsza tezy.
Macierz iteracji metody SOR ma postać
Niech teraz ![]() będzie wartością własną macierzy iteracji metody SOR,
będzie wartością własną macierzy iteracji metody SOR,
Ponieważ ![]() , mamy równoważnie
, mamy równoważnie
Zatem ![]() jest wartością własną
jest wartością własną ![]() wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy ![]() jest wartością własną macierzy
jest wartością własną macierzy ![]() .
.
W konsekwencji, jeśli tylko ![]() , to
, to ![]() jest wartością własną macierzy
jest wartością własną macierzy ![]() . Na mocy założenia,
. Na mocy założenia, ![]() ma te same wartości własne, co
ma te same wartości własne, co ![]() , co kończy dowód drugiej części twierdzenia. Dowód części trzeciej pozostawiamy jako ćwiczenie.
, co kończy dowód drugiej części twierdzenia. Dowód części trzeciej pozostawiamy jako ćwiczenie.
Wniosek 5.2 (O zbieżności metody Gaussa–Seidela)
Jeśli ![]() jest zgodnie uporządkowana i promień spektralny macierzy iteracji metody Jacobiego dla
jest zgodnie uporządkowana i promień spektralny macierzy iteracji metody Jacobiego dla ![]() jest równy
jest równy ![]() , to promień spektralny macierzy iteracji metody Gaussa–Seidela jest równy
, to promień spektralny macierzy iteracji metody Gaussa–Seidela jest równy ![]() . Znaczy to, że metoda Gaussa–Seidela jest dwukrotnie szybsza od metody Jacobiego.
. Znaczy to, że metoda Gaussa–Seidela jest dwukrotnie szybsza od metody Jacobiego.
Dowód
Rzeczywiście, na mocy twierdzenia Vargi, każdej niezerowej wartości własnej macierzy SOR odpowiada wartość własna macierzy iteracji Jacobiego ![]() , spełniająca równanie
, spełniająca równanie
Dla metody Gaussa–Seidela, ![]() , i w konsekwencji
, i w konsekwencji ![]() .
.
Korzystając z twierdzenia Vargi można udowodnić
Twierdzenie 5.7 (Twierdzenie Younga o optymalnym parametrze SOR)
Niech macierz ![]() będzie symetryczną macierzą zgodnie uporządkowaną i niech
będzie symetryczną macierzą zgodnie uporządkowaną i niech ![]() będzie równe promieniowi spektralnemu macierzy iteracji metody Jacobiego. Wtedy optymalna wartość parametru relaksacji
będzie równe promieniowi spektralnemu macierzy iteracji metody Jacobiego. Wtedy optymalna wartość parametru relaksacji ![]() , gwarantująca najmniejszy promień spektralny macierzy iteracji metody SOR, jest równa
, gwarantująca najmniejszy promień spektralny macierzy iteracji metody SOR, jest równa
Promień spektralny macierzy iteracji SOR z tym parametrem wynosi wtedy
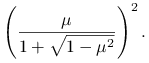 |
Dowód powyższego twierdzenia można znaleźć na przykład w [15, rozdział 8.3].
Jakkolwiek piękne teoretycznie, nawet twierdzenia Younga i Vargi są dość bezlitosne dla metody SOR w wielu praktycznych zastosowaniach.
Przykład 5.11
Dla macierzy jednowymiarowego laplasjanu rozmiaru ![]() , oznaczając
, oznaczając ![]() , mamy
, mamy ![]() i w konsekwencji
i w konsekwencji ![]() . Zatem, dla
. Zatem, dla ![]() , gdy
, gdy ![]() , promień spektralny macierzy iteracji SOR z optymalnym parametrem relaksacji jest równy aż
, promień spektralny macierzy iteracji SOR z optymalnym parametrem relaksacji jest równy aż ![]() , a więc jest praktycznie tak samo blisko jedności, jak w przypadku metody Jacobiego!
, a więc jest praktycznie tak samo blisko jedności, jak w przypadku metody Jacobiego!
Przykład 5.12
Kontynuując przykład 5.9, porównamy szybkość zbieżności metody SOR, Gaussa–Seidela (czyli SOR z parametrem ![]() ) i Jacobiego na tym samym, ekstremalnie trudnym dla metod iteracyjnych zadaniu. Na początek weźmiemy
) i Jacobiego na tym samym, ekstremalnie trudnym dla metod iteracyjnych zadaniu. Na początek weźmiemy ![]() i zbadamy zależność szybkości zbieżności SOR od wartości
i zbadamy zależność szybkości zbieżności SOR od wartości ![]() . Korzystając z wyniku poprzedniego przykładu, będziemy mogli także uruchomić SOR z optymalnym parametrem.
. Korzystając z wyniku poprzedniego przykładu, będziemy mogli także uruchomić SOR z optymalnym parametrem.
Zwróć uwagę na dramatyczną przewagę SOR z optymalnym parametrem nad metodą Gaussa–Seidela. Zbadaj, jak zmienią się wyniki, gdy wyraźnie zwiększysz ![]() , np. do tysiąca.
, np. do tysiąca.
Ćwiczenie 5.15
Gdy macierz iteracji ![]() metody stacjonarnej
metody stacjonarnej
jest daleka od normalnej, numeryczna realizacja iteracji w arytmetyce zmiennoprzecinkowej ograniczonej precyzji może napotkać na problemy: w początkowych iteracjach residuum może znacząco rosnąć, co w efekcie może doprowadzić do praktycznej utraty zbieżności.
Zbadaj to na przykładzie–zabawce (por. [2, 10.2.3]),
gdy ![]() . Wyznacz promień spektralny tej macierzy, jej normę, a także wykres normy
. Wyznacz promień spektralny tej macierzy, jej normę, a także wykres normy ![]() w zależności od
w zależności od ![]() .
.
Dla ![]() (wyraźnie większych od 1), macierz iteracji
(wyraźnie większych od 1), macierz iteracji ![]() , choć o promieniu spektralnym mniejszym niż 1, ma tę właściwość, że norma jej kolejnych potęg początkowo rośnie.
, choć o promieniu spektralnym mniejszym niż 1, ma tę właściwość, że norma jej kolejnych potęg początkowo rośnie.
lam = 0.9995; B = [lam 1; 0 lam]; resid=[]; x = [1;1]; for i = 1:100000, x = B*x; resid(i) = norm(x); end; semilogy(resid);
Ćwiczenie 5.16
Metoda Richardsona z parametrem ![]() jest określona wzorem
jest określona wzorem
Niech macierz ![]() będzie symetryczna.
będzie symetryczna.
Sprawdź, że jest to stacjonarna metoda iteracyjna oparta na rozszczepieniu
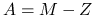 , gdzie
, gdzie 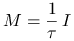 .
.Wykaż, że jeśli
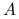 jest nieokreślona, dla żadnego wyboru
jest nieokreślona, dla żadnego wyboru 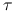 nie jest prawdą, że metoda Richardsona jest zbieżna do
nie jest prawdą, że metoda Richardsona jest zbieżna do 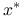 dla dowolnego
dla dowolnego 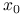 .
.Wykaż, że jeśli
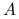 jest dodatnio określona, to metoda Richardsona jest zbieżna dla
jest dodatnio określona, to metoda Richardsona jest zbieżna dla 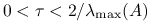 , a dla
, a dla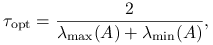
promień spektralny macierzy iteracji
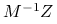 jest najmniejszy możliwy i równy
jest najmniejszy możliwy i równy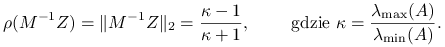
Ćwiczenie 5.17
Niech ![]() i niech istnieją stałe
i niech istnieją stałe ![]() takie, że dla każdego
takie, że dla każdego ![]()
Wykaż, że wtedy metoda Richardsona jest zbieżna w normie euklidesowej dla ![]() . Ponadto, jeśli
. Ponadto, jeśli ![]() , to współczynnik zbieżności
, to współczynnik zbieżności ![]() w tej normie można oszacować przez
w tej normie można oszacować przez 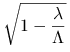 .
.
Ćwiczenie 5.18 (Hackbusch)
Niech ![]() będą macierzami symetrycznymi i dodatnio określonymi. Dla dwóch macierzy symetrycznych
będą macierzami symetrycznymi i dodatnio określonymi. Dla dwóch macierzy symetrycznych ![]() będziemy pisali
będziemy pisali ![]() , jeśli
, jeśli ![]() , czyli, innymi słowy, gdy
, czyli, innymi słowy, gdy ![]() dla każdego
dla każdego ![]() . Wykaż, że:
. Wykaż, że:
Jeśli
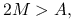
to iteracja
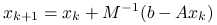
jest zbieżna, a dokładniej, macierz iteracji,
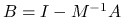 , spełnia
, spełnia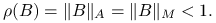
Jeśli dla pewnych
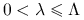 zachodzi
zachodzi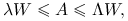
to wszystkie wartości własne
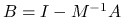 są rzeczywiste oraz
są rzeczywiste oraz 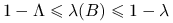 .
.
5.4. Metody blokowe
Pewnym remedium na powolną zbieżność metod stacjonarnych jest stosowanie metod blokowych, w których iterację konstruuje się tak jak dotychczas, ale zamiast na elementach, działa się na całych blokach macierzy (naturalnie, jeśli trzeba, musimy założyć ich odwracalność). Dla poprawienia zbieżności często stosuje się wariant z zakładką, zob. rysunek 5.6. W praktyce takie metody mogą być wyraźnie skuteczniejsze od dotychczas rozważanych: rzeczywiście, w skrajnym przypadku, pojedynczego ,,bloku” — rozmiaru ![]() — wszystkie wyżej omówione metody stacjonarne redukują się do metody bezpośredniej…
— wszystkie wyżej omówione metody stacjonarne redukują się do metody bezpośredniej…
Ciekawym i nietrywialnym uogólnieniem metod z zakładką jest addytywna metoda Schwarza: jeden z przedstawicieli klasy tzw. metod dekompozycji obszaru, będących bardzo efektywnymi i naturalnie równoległymi operatorami ściskającymi (mówimy o nich w rozdziale 7) dla dyskretyzacji równań różniczkowych cząstkowych, [14].
5.5. Metody projekcji
Dotychczas omówione metody opierają się na czysto formalnym, mechanicznym, podziale macierzy, bezpośrednio związanym z jej strukturą. Tymczasem można zdefiniować metody iteracyjne o podobnym koszcie iteracji, ale w których kolejne przybliżenia rozwiązania będziemy wybierać tak, by w jakimś sensie zminimalizować błąd.
Metodę iteracyjną będziemy definiować w formie aktualizacji poprzedniego przybliżenia,
,,Idealna poprawka” ![]() , oznaczmy ją
, oznaczmy ją ![]() , powinna spełniać więc równanie
, powinna spełniać więc równanie
bo wtedy dostalibyśmy ![]() . Ma ona jednak tę wadę, że do jej wyznaczenia musielibyśmy dokładnie rozwiązać nasz układ równań (co prawda z nieco inną prawą stroną, ale to bez znaczenia!) — a więc wpadlibyśmy z deszczu pod rynnę! Jednak, gdyby można było tanio rozwiązać ten układ równań w przybliżeniu, to może w ten sposób udałoby się nam określić zbieżną metodę?
. Ma ona jednak tę wadę, że do jej wyznaczenia musielibyśmy dokładnie rozwiązać nasz układ równań (co prawda z nieco inną prawą stroną, ale to bez znaczenia!) — a więc wpadlibyśmy z deszczu pod rynnę! Jednak, gdyby można było tanio rozwiązać ten układ równań w przybliżeniu, to może w ten sposób udałoby się nam określić zbieżną metodę?
Aby określić przybliżone rozwiązanie równania poprawki, najpierw przeformułujemy je nieco. Niech dwie macierze: ![]() i
i ![]() mają tę własność, że kolumny każdej z nich tworzą bazę
mają tę własność, że kolumny każdej z nich tworzą bazę ![]() . Wtedy rozwiązanie dokładne równania idealnej poprawki,
. Wtedy rozwiązanie dokładne równania idealnej poprawki, ![]() , możemy reprezentować w bazie
, możemy reprezentować w bazie ![]() ,
, ![]() dla pewnego
dla pewnego ![]() . Co więcej, z nieosobliwości macierzy
. Co więcej, z nieosobliwości macierzy ![]() i
i ![]() wynika, że
wynika, że
To daje nam pomysł na definicję przybliżonej poprawki idealnej: niech ![]() i
i ![]() będą macierzami pełnego rzędu, tego samego zadanego z góry rozmiaru
będą macierzami pełnego rzędu, tego samego zadanego z góry rozmiaru ![]() . Wtedy poprawkę
. Wtedy poprawkę ![]() określimy jako wektor
określimy jako wektor
taki, że ![]() spełnia równanie
spełnia równanie
| (5.20) |
Jest to właśnie metoda projekcji.
Ponieważ macierz zredukowana ![]() jest kwadratowa rozmiaru
jest kwadratowa rozmiaru ![]() , to
, to ![]() będzie tanie do wyznaczenia, gdy
będzie tanie do wyznaczenia, gdy ![]() jest niewielkie. Nazwa metody bierze się stąd, że z powyższej definicji wynika, że wektor residualny równania poprawki,
jest niewielkie. Nazwa metody bierze się stąd, że z powyższej definicji wynika, że wektor residualny równania poprawki, ![]() jest prostopadły do podprzestrzeni rozpiętej przez kolumny
jest prostopadły do podprzestrzeni rozpiętej przez kolumny ![]() :
:
Z drugiej strony, ![]() będzie dobrze określone tylko wtedy, gdy macierz zredukowana
będzie dobrze określone tylko wtedy, gdy macierz zredukowana ![]() będzie nieosobliwa — co nie zawsze musi być prawdą, nawet jeśli
będzie nieosobliwa — co nie zawsze musi być prawdą, nawet jeśli ![]() jest nieosobliwa (pomyśl o macierzy
jest nieosobliwa (pomyśl o macierzy ![]() i
i ![]() ). Aby zagwarantować sobie odwracalność macierzy zredukowanej, zwykle wybiera się macierz pełnego rzędu
). Aby zagwarantować sobie odwracalność macierzy zredukowanej, zwykle wybiera się macierz pełnego rzędu ![]() i w zależności od własności macierzy
i w zależności od własności macierzy ![]() dobiera się macierz
dobiera się macierz ![]() :
:
Jeśli
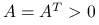 , to kładziemy
, to kładziemy 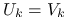 . Wtedy macierz zredukowana
. Wtedy macierz zredukowana 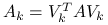 jest symetryczna i dodatnio określona.
jest symetryczna i dodatnio określona.Jeśli
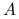 jest tylko nieosobliwa, to kładziemy
jest tylko nieosobliwa, to kładziemy 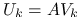 . Macierz zredukowana jest postaci
. Macierz zredukowana jest postaci 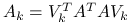 , a więc jest macierzą zredukowaną poprzedniego rodzaju, ale dla macierzy równań normalnych,
, a więc jest macierzą zredukowaną poprzedniego rodzaju, ale dla macierzy równań normalnych, 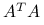 .
.
Jak możemy się domyślić, metody projekcji są metodami minimalizacji, co potwierdza poniższy dwuczęściowy lemat:
Lemat 5.1
Niech ![]() będzie zadaną macierzą
będzie zadaną macierzą ![]() , pełnego rzędu. Oznaczmy przez
, pełnego rzędu. Oznaczmy przez ![]() podprzestrzeń rozpiętą przez kolumny
podprzestrzeń rozpiętą przez kolumny ![]() .
.
Dowód zostawiamy jako ćwiczenie.
Ćwiczenie 5.19
Udowodnij lemat 5.1.
5.5.1. Metoda najszybszego spadku
Jednym z bardziej prominentnych przykładów metody projekcji jest metoda najszybszego spadku, działająca w przypadku, gdy macierz ![]() jest symetryczna i dodatnio określona. W tej metodzie wybieramy
jest symetryczna i dodatnio określona. W tej metodzie wybieramy ![]() . Ponieważ wymiar przestrzeni rozpiętej przez kolumny
. Ponieważ wymiar przestrzeni rozpiętej przez kolumny ![]() jest równy
jest równy ![]() , równanie poprawki upraszcza się do jednego równania skalarnego na
, równanie poprawki upraszcza się do jednego równania skalarnego na ![]() ,
,
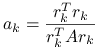 |
i w konsekwencji ![]() .
.
Nazwa metody wywodzi się stąd, że wektor poprawki w tej metodzie jest proporcjonalny do residuum, które z kolei jest kierunkiem gradientu funkcjonału ![]() w punkcie
w punkcie ![]() :
:
Twierdzenie 5.8 (o zbieżności metody najszybszego spadku)
W metodzie najszybszego spadku,
gdzie ![]() .
.
Dowód
Łatwo wykazać (por. [13, twierdzenie 5.2]), że jeśli ![]() ,
,
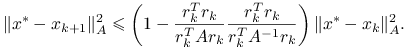 |
Teza wynika z lematu, którego elegancki dowód, pochodzący od Braessa, można znaleźć w [2]:
Lemat 5.2 (Kantorowicza)
Niech ![]() . Wtedy dla dowolnego
. Wtedy dla dowolnego ![]() ,
,
Ćwiczenie 5.20
Wykaż, że w metodzie najszybszego spadku zachodzi ![]() .
.
Ponieważ ![]() , to
, to
zatem
z definicji ![]() .
.
Przykład 5.13
Kontynuujemy przykład 5.8. Chcąc porównywać trzy metody: Jacobiego, Gaussa–Seidela oraz metodę najszybszego spadku, musimy zadbać o to, żeby były spełnione warunki zbieżności tej ostatniej — a więc, aby macierz ![]() była symetryczna i dodatnio określona. Dlatego, tym razem położymy, dla dodatniego
była symetryczna i dodatnio określona. Dlatego, tym razem położymy, dla dodatniego ![]() ,
,
Choć ![]() wydaje się dosyć gęsta, w rzeczywistości wciąż jest macierzą rzadką.
Zwróćmy uwagę nie tylko na samą szybkość zbieżności — mierzoną liczbą iteracji — ale także na efektywność metody: ile czasu zajmuje wyznaczenie przybliżenia z zadaną dokładnością. Metoda najszybszego spadku niewątpliwie ma najtańszą iterację (a najdroższą — metoda Gaussa–Seidela), co ostatecznie przekłada się na większą efektywność metody najszybszego spadku (pomimo mniejszej szybkości zbieżności).
wydaje się dosyć gęsta, w rzeczywistości wciąż jest macierzą rzadką.
Zwróćmy uwagę nie tylko na samą szybkość zbieżności — mierzoną liczbą iteracji — ale także na efektywność metody: ile czasu zajmuje wyznaczenie przybliżenia z zadaną dokładnością. Metoda najszybszego spadku niewątpliwie ma najtańszą iterację (a najdroższą — metoda Gaussa–Seidela), co ostatecznie przekłada się na większą efektywność metody najszybszego spadku (pomimo mniejszej szybkości zbieżności).
Ćwiczenie 5.21
Wyjaśnij, dlaczego w powyższym przykładzie, dla małych wartości ![]() , metoda Jacobiego czasem nie jest zbieżna.
, metoda Jacobiego czasem nie jest zbieżna.
Bo macierz ![]() nie musi być diagonalnie dominująca.
nie musi być diagonalnie dominująca.
Przykład 5.14
Dla macierzy jednowymiarowego laplasjanu, mamy
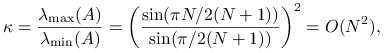 |
zatem dla ![]() mamy współczynnik redukcji błędu na poziomie
mamy współczynnik redukcji błędu na poziomie ![]() . Znaczy to dokładnie tyle, że metoda nie nadaje się do rozwiązywania takich zadań, gdy
. Znaczy to dokładnie tyle, że metoda nie nadaje się do rozwiązywania takich zadań, gdy ![]() jest duże. Szybkość zbieżności metody najszybszego spadku jest w naszym przykładzie porównywalna z szybkością metody Jacobiego i gorsza od metody SOR z optymalnym parametrem relaksacji.
jest duże. Szybkość zbieżności metody najszybszego spadku jest w naszym przykładzie porównywalna z szybkością metody Jacobiego i gorsza od metody SOR z optymalnym parametrem relaksacji.
5.5.2. Metoda najmniejszego residuum
Gdy o macierzy ![]() wiemy jedynie, że jest nieosobliwa, możemy zastosować metodę najmniejszego residuum. W tej metodzie wybieramy
wiemy jedynie, że jest nieosobliwa, możemy zastosować metodę najmniejszego residuum. W tej metodzie wybieramy ![]() oraz
oraz ![]() . Równanie poprawki znów upraszcza się do jednego równania skalarnego na
. Równanie poprawki znów upraszcza się do jednego równania skalarnego na ![]() ,
,
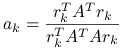 |
i w konsekwencji ![]() .
.
Twierdzenie 5.9
Załóżmy, że macierz ![]() jest dodatnio określona i oznaczmy
jest dodatnio określona i oznaczmy ![]() . Wtedy
. Wtedy
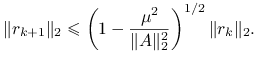 |
![]() nazywana jest częścią symetryczną macierzy
nazywana jest częścią symetryczną macierzy ![]() .
.
Ćwiczenie 5.22
Przeprowadź dowód twierdzenia o zbieżności metody najmniejszego residuum.
Zob. dowód twierdzenia 5.3 w [13].
Ćwiczenie 5.23
Przypuśćmy, że umiemy tanio rozwiązywać układy równań z (nieosobliwą) macierzą ![]() rozmiaru
rozmiaru ![]() . Niech będzie dana macierz
. Niech będzie dana macierz
gdzie ![]() oraz
oraz ![]() .
.
Wskaż warunek konieczny i dostateczny na to, by macierz
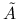 była nieosobliwa.
była nieosobliwa.Podaj możliwie tani algorytm rozwiązywania układu równań z macierzą
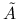 .
.
![]() jest nieosobliwa wtedy i tylko wtedy, gdy
jest nieosobliwa wtedy i tylko wtedy, gdy ![]() .
.
Ćwiczenie 5.24 (wzór Shermana–Morrisona)
Przypuśćmy, że umiemy tanio rozwiązywać układy równań z (nieosobliwą) macierzą ![]() rozmiaru
rozmiaru ![]() . Niech będzie dana macierz
. Niech będzie dana macierz
gdzie ![]() .
.
Wskaż warunek konieczny i dostateczny na to, by macierz
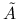 była nieosobliwa.
była nieosobliwa.Podaj możliwie tani algorytm rozwiązywania układu równań z macierzą
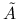 .
.
Ćwiczenie 5.25
Czy metodę iteracyjną warto stosować do rozwiązywania układu ![]() z macierzą
z macierzą ![]() , w przypadku, gdy
, w przypadku, gdy ![]() jest bardzo duże oraz
jest bardzo duże oraz ![]() jest rzadka?
jest rzadka?
Tutaj, jak wynika z naszych dotychczasowych rozważań, odpowiedź jest zniuansowana. Jedno mnożenie wektora przez ![]() kosztuje zapewne
kosztuje zapewne ![]() flopów, więc metoda iteracyjna będzie miała sens, gdy satysfakcjonujące przybliżenie dostaniemy po
flopów, więc metoda iteracyjna będzie miała sens, gdy satysfakcjonujące przybliżenie dostaniemy po ![]() iteracjach (a to, jak wiemy, nie zawsze jest gwarantowane). Z drugiej strony, może istnieć skuteczny reordering macierzy (czyli zmiana uporządkowania niewiadomych lub równań), pozwalający tanio wyznaczyć rozwiązanie metodą bezpośrednią [13].
iteracjach (a to, jak wiemy, nie zawsze jest gwarantowane). Z drugiej strony, może istnieć skuteczny reordering macierzy (czyli zmiana uporządkowania niewiadomych lub równań), pozwalający tanio wyznaczyć rozwiązanie metodą bezpośrednią [13].