Zagadnienia
8. Przegląd innych metod rozwiązywania wielkich układów równań liniowych
Na szczęście, nie ma jednej najlepszej metody rozwiązywania wielkich układów równań liniowych; czyni to oczywiście życie znacznie ciekawszym. Doprowadziło to do skonstruowania dużej liczby konkurencyjnych metod: zarówno bezpośrednich, jak i iteracyjnych. Celem nieniejszego rozdziału jest pobieżne zaznajomienie Czytelnika z niewielką ich reprezentacją. Dobór tej właściwej dla konkretnego zadania nie musi być oczywisty! Szerszy przegląd takich metod znajdziemy m.in. w monografii [13], [].
8.1. Inne metody Kryłowa
Na początek, na podstawie [1] przedstawimy w pewien systematyczny sposób uogólnienie metody CG na szerszą klasę problemów. Następnie zrobimy krótki przegląd wybranych metod Kryłowa, nie opartych na zasadzie minimalizacji.
8.1.1. Uogólnienia metody CG
Wielką zaletą metody PCG jest to, że nie wymaga ona pamiętania całej bazy przestrzeni Kryłowa ![]() , a iteracja ma prostą formułę
, a iteracja ma prostą formułę ![]() , gdzie
, gdzie ![]() jest tak dobrany by minimalizować pewną normę błędu. Można więc pójść krok dalej i określić całą klasę metod o podobnej strukturze.
jest tak dobrany by minimalizować pewną normę błędu. Można więc pójść krok dalej i określić całą klasę metod o podobnej strukturze.
Przyjmijmy więc, że
macierz
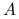 jest nieosobliwa (na tym poziomie ogólności nie zakładamy symetrii ani dodatniej określoności)
jest nieosobliwa (na tym poziomie ogólności nie zakładamy symetrii ani dodatniej określoności)
oraz są dane dwie dodatkowe macierze:
nieosobliwa macierz lewostronnie ściskająca
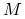 ,
,symetryczna, dodatnio określona macierz
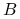 , która będzie definiować normę, w której będziemy minimalizować błąd:
, która będzie definiować normę, w której będziemy minimalizować błąd: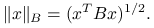
Będziemy zakładali, że macierz ściśnięta ![]() jest normalna względem iloczynu skalarnego indukowanego przez macierz
jest normalna względem iloczynu skalarnego indukowanego przez macierz ![]() , co możemy zapisać w formie warunku
, co możemy zapisać w formie warunku
gdzie ![]() .
.
W uogólnionej metodzie CG, którą będziemy oznaczali GCG(![]() ,
, ![]() ,
, ![]() ), kolejna iteracja
), kolejna iteracja ![]() będzie określona tak, by
będzie określona tak, by
| (8.1) |
Twierdzenie 8.1
Przy powyższych założeniach, metoda GCG(![]() ,
, ![]() ,
, ![]() ) jest dobrze określona i w dokładnej arytmetyce osiąga rozwiązanie dokładne po co najwyżej
) jest dobrze określona i w dokładnej arytmetyce osiąga rozwiązanie dokładne po co najwyżej ![]() krokach.
krokach.
Dowód
Kładąc ![]() oraz
oraz ![]() , możemy zastosować twierdzenie 6.1 do przestrzeni Kryłowa
, możemy zastosować twierdzenie 6.1 do przestrzeni Kryłowa ![]() , które zagwarantuje nam spełnienie tezy twierdzenia.
, które zagwarantuje nam spełnienie tezy twierdzenia.
Twierdzenie 8.2
Przy powyższych założeniach, błąd na ![]() -tym kroku metody GCG(
-tym kroku metody GCG(![]() ,
, ![]() ,
, ![]() ) spełnia oszacowanie
) spełnia oszacowanie
Dowód
Na mocy wniosku 6.1,
Ponieważ dla dowolnego ![]()
| (8.2) |
to w konsekwencji ![]() . Z założenia macierz
. Z założenia macierz ![]() jest normalna, jest więc diagonalizowalna i jej wektory własne są ortogonalne:
jest normalna, jest więc diagonalizowalna i jej wektory własne są ortogonalne:
Stąd zaś wynika, że ![]() , co kończy dowód, gdyż macierze
, co kończy dowód, gdyż macierze ![]() i
i ![]() są podobne, więc mają to samo spektrum.
są podobne, więc mają to samo spektrum.
Ćwiczenie 8.1
Udowodnij równość (8.2).
Można, postępując analogicznie jak w przypadku klasycznej metody CG wykazać, że GCG(![]() ,
, ![]() ,
, ![]() ) ma własności podobne jak jej protoplastka:
) ma własności podobne jak jej protoplastka:
Stwierdzenie 8.1
W metodzie GCG(![]() ,
, ![]() ,
, ![]() ) zachodzi:
) zachodzi:
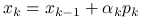 , gdzie
, gdzie 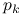 tworzą bazę
tworzą bazę 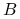 -ortogonalną przestrzeni Kryłowa
-ortogonalną przestrzeni Kryłowa 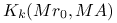 .
.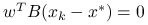 dla każdego
dla każdego 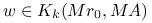 .
.
Dowód
W oczywisty sposób ![]() , gdzie
, gdzie ![]() . Jeśli przez
. Jeśli przez ![]() oznaczyć bazę w
oznaczyć bazę w ![]() , to
, to ![]() i na mocy (6.2)
i na mocy (6.2) ![]() spełnia układ równań normalnych,
spełnia układ równań normalnych,
Ponieważ ![]() , dostajemy
, dostajemy
co dowodzi drugiego punktu.
∎Metodę GCG(![]() ,
, ![]() ,
, ![]() ) możnaby zrealizować następującym uogólnieniem algorytmu CG, który nazwiemy za [1] algorytmem Odir(
) możnaby zrealizować następującym uogólnieniem algorytmu CG, który nazwiemy za [1] algorytmem Odir(![]() ,
, ![]() ,
, ![]() ):
):
Metoda Odir dla GCG, wersja bazowa
| while not stop begin |
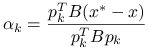 |
| |
| |
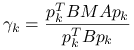 |
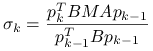 |
| |
| |
| end |
Algorytm ten jeszcze nie jest gotowy do użycia, albowiem wymaga obliczania ![]() — a więc potencjalnie wymaga odwołania się do nieznanego a priori wektora błędu! Możliwość skutecznego obliczania współczynnika
— a więc potencjalnie wymaga odwołania się do nieznanego a priori wektora błędu! Możliwość skutecznego obliczania współczynnika ![]() ogranicza więc zbiór
ogranicza więc zbiór ![]() , których możemy użyć do zdefiniowania konkretnej metody. Z drugiej strony, wybierając konkretne
, których możemy użyć do zdefiniowania konkretnej metody. Z drugiej strony, wybierając konkretne ![]() możemy dalej uprościć powyższą bazową implementację. Na tym etapie nie jest także oczywiste, czy może zdarzyć się
możemy dalej uprościć powyższą bazową implementację. Na tym etapie nie jest także oczywiste, czy może zdarzyć się ![]() — a więc stagnacja i załamanie się algorytmu (dzielenie przez zero!).
— a więc stagnacja i załamanie się algorytmu (dzielenie przez zero!).
Wśród metod, które dają się skutecznie zaimplementować na podstawie algorytmu Odir(![]() ,
, ![]() ,
, ![]() ) — to znaczy: mają obliczalne
) — to znaczy: mają obliczalne ![]() — znajdują się metody wymienione w tabeli 8.1, którą przytaczamy za [1, Table 5.2]. Z tabeli wynika m.in., że PCG wcale nie wymaga dodatnio określonej macierzy ściskającej!
— znajdują się metody wymienione w tabeli 8.1, którą przytaczamy za [1, Table 5.2]. Z tabeli wynika m.in., że PCG wcale nie wymaga dodatnio określonej macierzy ściskającej!
| Metoda | Ograniczenia | ||
|---|---|---|---|
| CG | |||
| CR | |||
| PCG |
|
||
| PCR |
|
||
| CGNR | |||
| CGNE | |||
| D'yakonov |
Aby otrzymać dobrą implementację konkretnej metody opartej na algorytmie Odir, należy zawsze ją dopracować, wykorzystując zależności specyficzne dla konkretnej metody.
Warta uwagi jest metoda PCR, która działa w przypadku, gdy macierz ![]() jest jedynie symetryczna — nie musi być dodatnio określona. Metoda D'aykonova [6] co prawda działa dla dowolnej nieosobliwej, niesymetrycznej macierzy
jest jedynie symetryczna — nie musi być dodatnio określona. Metoda D'aykonova [6] co prawda działa dla dowolnej nieosobliwej, niesymetrycznej macierzy ![]() , ale ze względu na jej podobieństwo do równań normalnych dla
, ale ze względu na jej podobieństwo do równań normalnych dla ![]() , w wielu wypadkach skuteczniejsza (pod względem szybkości zbieżności, a nie pod względem oszczędności pamięci) będzie metoda typu GMRES.
, w wielu wypadkach skuteczniejsza (pod względem szybkości zbieżności, a nie pod względem oszczędności pamięci) będzie metoda typu GMRES.
Uwaga 8.1
Czasami wymaganie, by można było wykonywać mnożenie przez ![]() może być trudne do spełnienia — na przykład wtedy, gdy
może być trudne do spełnienia — na przykład wtedy, gdy ![]() jest zadana jako operator, tzn. wyłącznie przez procedurę mnożenia przez zadany wektor
jest zadana jako operator, tzn. wyłącznie przez procedurę mnożenia przez zadany wektor ![]() , tzn. obliczania
, tzn. obliczania ![]() .
.
Ćwiczenie 8.2
Porównaj zbieżność metod: PCG i PCR w przypadku, gdy ![]() oraz
oraz ![]() są macierzami symetrycznymi i dodatnio określonymi. Przeprowadź weryfikację eksperymentalną swoich przypuszczeń.
są macierzami symetrycznymi i dodatnio określonymi. Przeprowadź weryfikację eksperymentalną swoich przypuszczeń.
W MATLABie dyponujesz gotową implementacją zarówno metody pcg, jak i pcr.
8.1.2. Metody nie oparte na minimalizacji
Zamiast określać kolejną iterację metody, jak dotychczas, przez pewien warunek minimalizacji, możemy inaczej położyć warunek na ![]() . Na przykład, możemy wymagać by oprócz
. Na przykład, możemy wymagać by oprócz ![]() zachodził warunek ortogonalności residuów:
zachodził warunek ortogonalności residuów:
(Zwróć uwagę na to, że residua mają być ortogonalne nie do ![]() , tylko do
, tylko do ![]() .)
.)
Tego typu warunek prowadzi m.in. do metody BiCG (ang. Bi-Conjugate Gradient) która wymaga mnożenia przez ![]() i nie jest też zbyt stabilna. Jej modyfikacje: CGS i BiCG-stab — nie wymagają już mnożenia przez
i nie jest też zbyt stabilna. Jej modyfikacje: CGS i BiCG-stab — nie wymagają już mnożenia przez ![]() , BiCG-stab jest też bardziej stabilna. Niestety, jak na razie dla BiCG-stab nie ma pełnej i satysfakcjonującej teorii zbieżności.
, BiCG-stab jest też bardziej stabilna. Niestety, jak na razie dla BiCG-stab nie ma pełnej i satysfakcjonującej teorii zbieżności.
W przeciwieństwie do metod minimalizacji, kolejna iteracja może nie być realizowalna mimo, że nie osiągnięto jeszcze rozwiązania — mówimy wtedy potocznie o załamaniu się metody (ang. breakdown).
W innej metodzie, QMR (ang. Quasi-Minimal Residual) — i jej wariancie bez mnożenia przez macierz transponowaną: TFQMR (ang. Transpose-Free QMR) — kolejną iterację wybiera się tak, by zminimalizować (stosunkowo łatwą do obliczenia) wielkość, która ma tylko trochę wspólnego z normą residuum.
Można pokazać [9], że metoda TFQMR dla macierzy ![]() (realizowana w dokładnej arytmetyce) w ciągu
(realizowana w dokładnej arytmetyce) w ciągu ![]() iteracji albo załamie się, albo osiągnie dokładne rozwiązanie.
iteracji albo załamie się, albo osiągnie dokładne rozwiązanie.
8.2. Metody strukturalne
W bardzo wielu przypadkach, w macierzach układów równań jakie przychodzi nam rozwiązywać w praktycznych zastosowaniach, nie tylko niewiadome są powiązane jedynie z nielicznymi innymi niewiadomymi (co właśnie prowadzi do rozrzedzenia macierzy) ale w dość naturalny sposób można wskazać grupy niewiadomych i równań, które między sobą nie mają żadnych powiązań.
W najogólniejszym przypadku, mielibyśmy więc
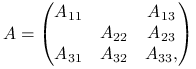 |
(8.3) |
gdzie ![]() są pewnymi macierzami kwadratowymi. Niewiadome i równania z grupy ,,
są pewnymi macierzami kwadratowymi. Niewiadome i równania z grupy ,,![]() ” nie mają bezpośredniego związku z grupą ,,
” nie mają bezpośredniego związku z grupą ,,![]() ” (są one powiązane ze sobą jedynie poprzez równania i niewiadome grupy ,,
” (są one powiązane ze sobą jedynie poprzez równania i niewiadome grupy ,,![]() ”). W dalszym ciągu będziemy zakładać, że macierze
”). W dalszym ciągu będziemy zakładać, że macierze ![]() i
i ![]() są nieosobliwe.
Strukturalizacja równania liniowego to nic innego jak wskazanie pewnej permutacji równań i niewiadomych, w wyniku której dostajemy układ postaci (8.3).
W rzeczywistości, dla macierzy
są nieosobliwe.
Strukturalizacja równania liniowego to nic innego jak wskazanie pewnej permutacji równań i niewiadomych, w wyniku której dostajemy układ postaci (8.3).
W rzeczywistości, dla macierzy ![]() i
i ![]() mogłyby zachodzić podobne relacje10Taką permutację nazywamy wtedy zagnieżdżonym podziałem grafu macierzy (ang. nested dissection)., jak w poniższym przykładzie.
mogłyby zachodzić podobne relacje10Taką permutację nazywamy wtedy zagnieżdżonym podziałem grafu macierzy (ang. nested dissection)., jak w poniższym przykładzie.
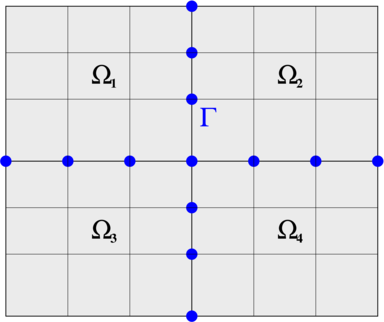
Przykład 8.1 (Strukturalizacja dyskretyzacji równania różniczkowego)
Rozważmy dyskretyzację równania różniczkowego
z jednorodnymi warunkami brzegowymi Dirichleta. Jeśli obszar ![]() podzielić na kilka mniejszych części, podobszarów,
podzielić na kilka mniejszych części, podobszarów, ![]() i przez
i przez ![]() oznaczyć zestaw krawędzi (ang. interface) je spajających:
oznaczyć zestaw krawędzi (ang. interface) je spajających: ![]() , to — ze względu na lokalny charakter działania pochodnej (i jej sensownych aproksymacji) — niewiadome z dwóch różnych podobszarów
, to — ze względu na lokalny charakter działania pochodnej (i jej sensownych aproksymacji) — niewiadome z dwóch różnych podobszarów ![]() i
i ![]() nie będą ze sobą powiązane. Będą za to powiązane z niewiadomymi leżącymi na krawędziach spajających
nie będą ze sobą powiązane. Będą za to powiązane z niewiadomymi leżącymi na krawędziach spajających ![]() , por. rysunek 8.1.
, por. rysunek 8.1.
Numerując niewiadome tak, by ![]() , gdzie wektor
, gdzie wektor ![]() zawiera niewiadome odpowiadające wewnętrznym węzłom w
zawiera niewiadome odpowiadające wewnętrznym węzłom w ![]() , a
, a ![]() — niewiadome odpowiadające węzłom na interfejsie
— niewiadome odpowiadające węzłom na interfejsie ![]() ,
otrzymalibyśmy macierz o blokowej strukturze
,
otrzymalibyśmy macierz o blokowej strukturze
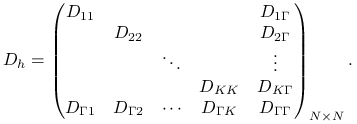 |
(8.4) |
W pustych miejscach ![]() znajdują się bloki zerowe, a macierze
znajdują się bloki zerowe, a macierze ![]() faktycznie są nieosobliwe.
faktycznie są nieosobliwe.
Dzięki szczególnej postaci macierzy (8.3) możemy podać algorytm typu ,,dziel i rządź” rozwiązywania układu równań ![]() z tą macierzą. Wprowadzając podział niewiadomych i wektora prawej strony zgodnie z blokowym podziałem macierzy
z tą macierzą. Wprowadzając podział niewiadomych i wektora prawej strony zgodnie z blokowym podziałem macierzy ![]() zadanym (8.3) mamy do rozwiązania układ
zadanym (8.3) mamy do rozwiązania układ
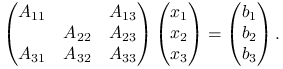 |
Dokonując blokowej eliminacji Gaussa (najpierw na blokach ![]() i
i ![]() ) dostajemy następujący algorytm:
) dostajemy następujący algorytm:
Oblicz
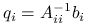 ,
, 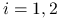 .
.Wyznacz
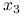 jako rozwiązanie układu
jako rozwiązanie układu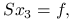
gdzie
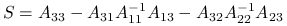 oraz
oraz 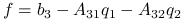 .
.Wyznacz
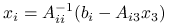 ,
, 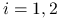 .
.
Oczywiście, wszędzie tam, gdzie występują odwrotności macierzy, w praktyce będziemy rozwiązywali układy równań z tymi macierzami.
Zwróćmy uwagę na kilka charakterystycznych cech tego algorytmu:
Zarówno w kroku 1. jak i w kroku 3. algorytmu, oba układy możemy rozwiązywać niezależnie od siebie (co daje możliwość równoległej implementacji).
Macierze
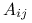 są rozrzedzone (bo
są rozrzedzone (bo 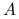 taka była), ale w ogólności
taka była), ale w ogólności 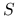 jest macierzą gęstszą.
jest macierzą gęstszą.
Jeśli wymiar macierzy ![]() jest niezbyt wielki, możemy ją wyznaczyć explicite i rozwiązać metodą bezpośrednią. Jednak jeśli
jest niezbyt wielki, możemy ją wyznaczyć explicite i rozwiązać metodą bezpośrednią. Jednak jeśli ![]() wciąż jest zbyt wielka (lub zbyt gęsta), by potraktować ją metodą bezpośrednią — wtedy możemy zastosować do niej metodę iteracyjną operatorową (matrix-free). Rzeczywiście, mnożenie macierzy
wciąż jest zbyt wielka (lub zbyt gęsta), by potraktować ją metodą bezpośrednią — wtedy możemy zastosować do niej metodę iteracyjną operatorową (matrix-free). Rzeczywiście, mnożenie macierzy ![]() przez wektor
przez wektor ![]() można zrealizować bez wyznaczania niej samej:
można zrealizować bez wyznaczania niej samej:
(Nawiasy wskazują kolejność mnożenia.) Możemy więc wyznaczyć iloczyn ![]() kosztem rozwiązania układów równań z macierzami
kosztem rozwiązania układów równań z macierzami ![]() i
i ![]() (co i tak musielibyśmy umieć zrobić!) oraz niewielkim dodatkowym kosztem pomnożenia pewnych wektorów przez rozrzedzone macierze trzeciej kolumny i trzeciego wiersza
(co i tak musielibyśmy umieć zrobić!) oraz niewielkim dodatkowym kosztem pomnożenia pewnych wektorów przez rozrzedzone macierze trzeciej kolumny i trzeciego wiersza ![]() .
.
Ćwiczenie 8.3
Przedyskutuj, jak rozwiązywać układ równań postaci (8.4).
8.3. Metody wielosiatkowe
Macierze rozrzedzone, które otrzymuje się z dyskretyzacji równań różniczkowych cząstkowych metodą różnic skończonych lub elementu skończonego, mają wiele specjalnych cech, które pozwalają na konstrukcję optymalnych metod rozwiązywania takich zadań. Jedną z takich klas metod są metody wielosiatkowe (ang. multigrid).
Omówimy jej ideę na przykładzie macierzy ![]() dyskretyzacji jednowymiarowego laplasjanu (5.5): wszystkie istotne wady metod iteracyjnych ujawniają się już w jej przypadku, podobnie jak zasadnicze cechy metody wielosiatkowej. Oczywiście, w praktyce metodę wielosiatkową stosowalibyśmy dopiero do dyskretyzacji dwu- lub trójwymiarowego laplasjanu.
dyskretyzacji jednowymiarowego laplasjanu (5.5): wszystkie istotne wady metod iteracyjnych ujawniają się już w jej przypadku, podobnie jak zasadnicze cechy metody wielosiatkowej. Oczywiście, w praktyce metodę wielosiatkową stosowalibyśmy dopiero do dyskretyzacji dwu- lub trójwymiarowego laplasjanu.
Gdyby przyjrzeć się metodzie Jacobiego dla ![]() zobaczymy, że niektóre składowe błędu są w niej szybciej redukowane niż inne. Dokładniej, rozważmy metodę Jacobiego z parametrem relaksacyjnym
zobaczymy, że niektóre składowe błędu są w niej szybciej redukowane niż inne. Dokładniej, rozważmy metodę Jacobiego z parametrem relaksacyjnym ![]() ,
,
(w macierzy ![]() diagonala jest stała równa
diagonala jest stała równa ![]() ). Macierz iteracji tej metody ma postać
). Macierz iteracji tej metody ma postać
Wyrażając błąd ![]() w bazie wektorów własnych macierzy
w bazie wektorów własnych macierzy ![]() (są dane wzorem
(są dane wzorem ![]() — por. (5.18)) dostajemy, że
— por. (5.18)) dostajemy, że
i w konsekwencji,
Jasne jest więc, że najszybszej redukcji ulegną te składowe błędu, które odpowiadają najbliższym zera wartościom ![]() , najwolniej zaś będą znikać te, dla których
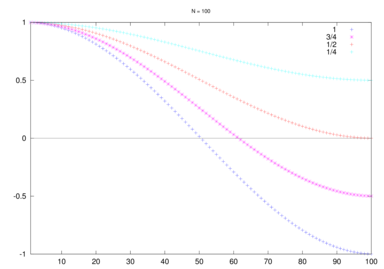
, najwolniej zaś będą znikać te, dla których ![]() będzie duży. Rysunek 8.2 przedstawia wykres
będzie duży. Rysunek 8.2 przedstawia wykres
w zależności od parametru relaksacyjnego ![]() .
.
Jak możemy zauważyć, gdy ![]() (tzn. gdy używamy standardowej metody Jacobiego), najsłabiej są redukowane składowe szybkozmienne i wolnozmienne (jedynie te ,,średniozmienne” są redukowane błyskawicznie).
(tzn. gdy używamy standardowej metody Jacobiego), najsłabiej są redukowane składowe szybkozmienne i wolnozmienne (jedynie te ,,średniozmienne” są redukowane błyskawicznie).
Ale już dla ![]() , najmocniej są redukowane wszystkie szybkozmienne składowe błędu — zatem po kilku iteracjach takiej metody błąd zostanie wygładzony. Jeśliby więc wspomóc taką prostą iterację poprawką, która redukowałaby pozostałe — wolnozmienne — składowe błędu, moglibyśmy otrzymać szybko zbieżną iterację. Jak pamiętamy z wcześniejszego wykładu, metody projekcji zastępowały idealną poprawkę
, najmocniej są redukowane wszystkie szybkozmienne składowe błędu — zatem po kilku iteracjach takiej metody błąd zostanie wygładzony. Jeśliby więc wspomóc taką prostą iterację poprawką, która redukowałaby pozostałe — wolnozmienne — składowe błędu, moglibyśmy otrzymać szybko zbieżną iterację. Jak pamiętamy z wcześniejszego wykładu, metody projekcji zastępowały idealną poprawkę ![]() poprawką przybliżoną
poprawką przybliżoną ![]() , wyznaczaną przez rozwiązanie zadania zmniejszonego wymiaru. W metodzie dwusiatkowej poprawkę wyznaczymy podobnie: rozwiązując metodą bezpośrednią (np. eliminacji Gaussa) równanie poprawki na rzadszej siatce — wszak będzie ono tylko gorszą aproksymacją (o mniejszej rozdzielczości!) tego samego rozwiązania równania Poissona, które ma aproksymować
, wyznaczaną przez rozwiązanie zadania zmniejszonego wymiaru. W metodzie dwusiatkowej poprawkę wyznaczymy podobnie: rozwiązując metodą bezpośrednią (np. eliminacji Gaussa) równanie poprawki na rzadszej siatce — wszak będzie ono tylko gorszą aproksymacją (o mniejszej rozdzielczości!) tego samego rozwiązania równania Poissona, które ma aproksymować ![]() .
.
W metodzie wielosiatkowej zadanie na rzadszej siatce (potrzebne do wyznaczenia poprawki na siatce najdrobniejszej) potraktujemy rekurencyjnie w ten sam sposób, otrzymując sekwencję zadań coraz mniejszego rozmiaru, którą w pewnym momencie oczywiście będziemy musieli przerwać i rozwiązać zadanie bardzo małego wyniaru metodą bezpośrednią.
Oto więc kolejne etapy jednej iteracji metody wielosiatkowej, wyznaczającej kolejne przybliżenie ![]() na podstawie
na podstawie ![]() :
:
Wygładzenie (ang. pre-smoothing) — zaczynając od
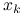 , wykonujemy kilka iteracji (zwykle jedną lub dwie) prostej metody typu Jacobiego lub Gaussa–Seidela z właściwie dobranym parametrem
, wykonujemy kilka iteracji (zwykle jedną lub dwie) prostej metody typu Jacobiego lub Gaussa–Seidela z właściwie dobranym parametrem 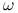 . Dostajemy przybliżenie pośrednie
. Dostajemy przybliżenie pośrednie 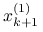 , ze zredukowaną szybkozmienną składową błędu.
, ze zredukowaną szybkozmienną składową błędu.Restrykcja — sformułowanie na rzadszej siatce zadania na poprawkę
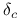 dla
dla 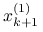 .
.Gruba poprawka (ang. coarse grid correction) — wyznaczenie poprawki
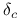 na rzadszej siatce — przez iterację taką, jak ta! (Jako przybliżenie początkowe dla
na rzadszej siatce — przez iterację taką, jak ta! (Jako przybliżenie początkowe dla 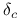 sensownie wziąć zero.)
sensownie wziąć zero.)Przedłużenie — wyrażenie poprawki obliczonej na rzadszej siatce w terminach wartości na gęstej siatki. Uwzględnienie poprawki i aktualizacja przybliżenia:
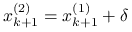 .
.Dodatkowe wygładzenie (ang. post-smoothing) — ewentualnie. Znów kilka iteracji jak na pierwszym etapie, z przybliżeniem początkowym równym
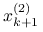 , zakończone wyznaczeniem
, zakończone wyznaczeniem 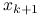 . Gdy ten etap jest pominięty, za
. Gdy ten etap jest pominięty, za 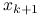 bierze się
bierze się 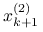 .
.
Okazuje się, że w ten sposób uzyskujemy metodę, której szybkość zbieżności na modelowym zadaniu nie zależy od parametru dyskretyzacji ![]() (a więc i od rozmiaru zadania). Przypomnijmy, że było to zmorą wszystkich dotychczas rozważanych metod iteracyjnych; aby to przezwyciężyć, musieliśmy tam użyć spektralnie równoważnej macierzy ściskającej. Metoda wielosiatkowa nie potrzebuje tego, co więcej, można pokazać, że koszt jednej iteracji metody jest rzędu
(a więc i od rozmiaru zadania). Przypomnijmy, że było to zmorą wszystkich dotychczas rozważanych metod iteracyjnych; aby to przezwyciężyć, musieliśmy tam użyć spektralnie równoważnej macierzy ściskającej. Metoda wielosiatkowa nie potrzebuje tego, co więcej, można pokazać, że koszt jednej iteracji metody jest rzędu ![]() — a więc (z dokładnością do stałej…) taki sam, jak koszt np. jednej iteracji metody CG.
— a więc (z dokładnością do stałej…) taki sam, jak koszt np. jednej iteracji metody CG.
Pełna metoda wielosiatkowa
Idąc dalej tym tropem możemy zauważyć, że jako dobre przybliżenie początkowe dla (iteracyjnej) metody wielosiatkowej można byłoby wybrać przybliżone rozwiązanie na rzadszej siatce: wtedy jedynymi istotnymi składowymi błędu na gęstej siatce byłyby składowe szybkozmienne — a te wyeliminowalibyśmy w kilku iteracjach! Oczywiście, wymagane przybliżenie na rzadszej siatce uzyskalibyśmy w ten sam sposób z jeszcze rzadszej siatki; na siatce o największych oczkach moglibyśmy użyć jakiejś metody bezpośredniej.
Pamiętając, że rozwiązywane przez nas zagadnienie — układ równań liniowych — pochodzi z dyskretyzacji pewnego równania różniczkowego musimy zdać sobie sprawę z tego, że nie ma sensu rozwiązywać go z dokładnością większą niż dokładność aproksymacji samej dyskretyzacji! Dlatego iterację można przerwać po osiągnięciu z góry zadanego poziomu błędu aproksymacji rozwiązania zadania różniczkowego. Gdy będziemy startować z przybliżenia wyznaczonego metodą opisaną powyżej, okazuje się, że często wystarczy tylko niewielka, niezależna od ![]() , liczba iteracji by osiągnąć zadany poziom błędu.
, liczba iteracji by osiągnąć zadany poziom błędu.
Taka metoda wyznaczania rozwiązania zadania powstałego po dyskretyzacji równania różniczkowego — którą tutaj tylko zasygnalizowaliśmy w uproszczeniu — nazywa się pełną metodą wielosiatkową (ang. full multigrid). Choć wciąż jest to metoda iteracyjna, ma ona cechy metody bezpośredniej. Okazuje się, że koszt wyznaczenia rozwiązania tą metodą jest rzędu ![]() (kilku iteracji metody wielosiatkowej na finalnej, najdrobniejszej siatce) — a więc optymalny co do rzędu, gdyż samych niewiadomych w zadaniu jest
(kilku iteracji metody wielosiatkowej na finalnej, najdrobniejszej siatce) — a więc optymalny co do rzędu, gdyż samych niewiadomych w zadaniu jest ![]() .
.