Zagadnienia
11. Metoda elementu skończonego - wprowadzenie
W tym rozdziale przedstawimy główne idee metody elementu skończonego na przykładzie modelowego zadania eliptycznego rzędu dwa na obszarze jednowymiarowym. Metoda elementu skończonego jest bardziej ogólna od metody różnic skończonych nawet dla zadań różniczkowych zadanych na obszarze w jednym wymiarze. Np. konstrukcje zadań przybliżonych dla warunków brzegowych różnego typu są dużo prostsze niż w przypadku metody różnic skończonych.
11.1. Metoda elementu skończonego dla modelowego zadania eliptycznego w jednym wymiarze
11.1.1. Słabe sformułowanie
Rozpatrzmy modelowe zadanie jednowymiarowe (7.1) z zerowymi warunkami brzegowymi i ![]() , którego rozwiązanie oznaczymy
, którego rozwiązanie oznaczymy ![]() .
.
Następnie weźmy dowolną funkcję ciągłą ![]() , która jest kawałkami
, która jest kawałkami ![]() na odcinku, tzn. która ma ciągłą pochodną poza skończoną ilością punktów taką, że
na odcinku, tzn. która ma ciągłą pochodną poza skończoną ilością punktów taką, że ![]() . Przemnóżmy równanie
. Przemnóżmy równanie ![]() przez tę funkcję. Ze wzoru na całkowanie przez części otrzymujemy:
przez tę funkcję. Ze wzoru na całkowanie przez części otrzymujemy:
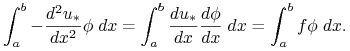 |
Oczywiście tutaj ![]() jest zdefiniowana poza skończoną ilością punktów nieciągłości.
jest zdefiniowana poza skończoną ilością punktów nieciągłości.
Zamiast zadania (7.1) możemy rozpatrzyć zadanie znalezienia
funkcji ![]() w odpowiedniej przestrzeni
w odpowiedniej przestrzeni ![]() funkcji określonych na odcinku
funkcji określonych na odcinku ![]() zawierających funkcje kawałkami
zawierających funkcje kawałkami ![]() i zerujące się w końcach odcinka (na razie nie ustalajmy precyzyjnie o jaką przestrzeń chodzi) takiej, żeby
i zerujące się w końcach odcinka (na razie nie ustalajmy precyzyjnie o jaką przestrzeń chodzi) takiej, żeby
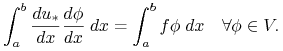 |
(11.1) |
Oczywiście rozwiązanie (7.1) spełnia (11.1), a przy odpowiednim doborze ![]() (oraz dostatecznej gładkości
(oraz dostatecznej gładkości ![]() ) można pokazać, że rozwiązanie (11.1) również spełnia (7.1). Zadanie (11.1) nazywamy sformułowaniem uogólnionym (słabym, wariacyjnym) zadania (7.1). Zaś (7.1) nazywamy sformułowaniem klasycznym.
Metoda elementu skończonego, która jest szczególnym przypadkiem metody Galerkina polega na tym, że wprowadzamy w specjalny sposób skończenie wymiarową podprzestrzeń przestrzeni
) można pokazać, że rozwiązanie (11.1) również spełnia (7.1). Zadanie (11.1) nazywamy sformułowaniem uogólnionym (słabym, wariacyjnym) zadania (7.1). Zaś (7.1) nazywamy sformułowaniem klasycznym.
Metoda elementu skończonego, która jest szczególnym przypadkiem metody Galerkina polega na tym, że wprowadzamy w specjalny sposób skończenie wymiarową podprzestrzeń przestrzeni ![]() .
Następnie szukamy rozwiązania w tej przestrzeni dyskretnej, które spełnia
zadanie wariacyjne (11.1) z tym, że przestrzeń
.
Następnie szukamy rozwiązania w tej przestrzeni dyskretnej, które spełnia
zadanie wariacyjne (11.1) z tym, że przestrzeń ![]() jest zastąpiona przez naszą dyskretną podprzestrzeń.
jest zastąpiona przez naszą dyskretną podprzestrzeń.
Proszę zauważyć, że podejście wariacyjne jest inne od metody różnic skończonych, w której konstrukcja rozwiązania określonego na zbiorze dyskretnym (siatce) polega na zastąpieniu odpowiednich pochodnych w równaniu różniczkowym odpowiednimi ilorazami różnicowymi na tej siatce.
11.1.2. Element liniowy
Wprowadźmy podział (triangulacje) odcinka ![]() na pododcinki (elementy)
na pododcinki (elementy) ![]() , gdzie
, gdzie
![]() dla
dla ![]() .
Za parametr tego podziału przyjmijmy
.
Za parametr tego podziału przyjmijmy ![]() , a punkty
, a punkty ![]() nazwiemy punktami nodalnymi (węzłami) tego podziału.
nazwiemy punktami nodalnymi (węzłami) tego podziału.
Oczywiście najprostszym podziałem jest podział równomierny, jeśli bierzemy ![]() dla
dla ![]() .
.
Zakładamy, że rozpatrujemy rodzinę podziałów z ![]() dążącym do zera.
dążącym do zera.
Teraz na bazie danego podziału ![]() możemy wprowadzić
przestrzeń dyskretną:
możemy wprowadzić
przestrzeń dyskretną:
gdzie ![]() jest przestrzenią wielomianów liniowych, tzn. stopnia nie większego niż jeden.
Funkcje z tej przestrzeni to funkcje kawałkami liniowe (czyli klasyczne splajny liniowe) z zerowymi warunkami brzegowymi na brzegu, czyli w szczególności są to funkcje ciągłe kawałkami klasy
jest przestrzenią wielomianów liniowych, tzn. stopnia nie większego niż jeden.
Funkcje z tej przestrzeni to funkcje kawałkami liniowe (czyli klasyczne splajny liniowe) z zerowymi warunkami brzegowymi na brzegu, czyli w szczególności są to funkcje ciągłe kawałkami klasy ![]() , zatem
, zatem ![]() .
.
Zadanie dyskretne polega na znalezieniu ![]() takiego, że
takiego, że
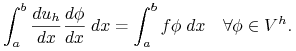 |
(11.2) |
Pozostawimy jako zadanie wykazanie istnienia jednoznacznego rozwiązania (11.2).
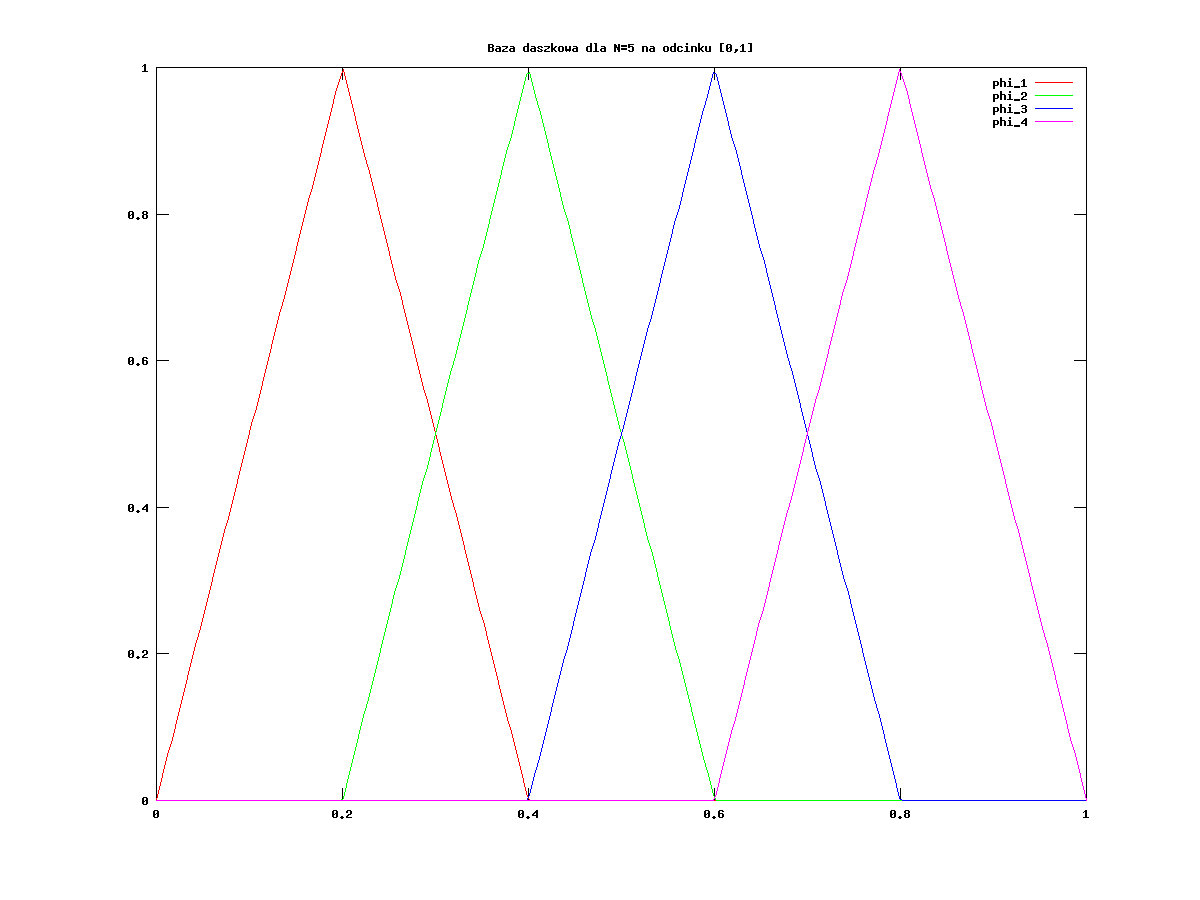
Na razie wprowadźmy tzw. funkcję nodalną: niech ![]() dla
dla ![]() będzie taką funkcją, że
będzie taką funkcją, że ![]() i
i ![]() dla
dla ![]() . Możemy podać wzór na taką funkcję:
. Możemy podać wzór na taką funkcję:
![\phi(x)=\left\{\begin{array}[]{lcl}0&&x\not\in[x_{{k-1}},x_{{k+1}}],\\
\frac{x-x_{{k-1}}}{x_{k}-x_{{k-1}}}&&x\in[x_{{k-1}},x_{k}],\\
1-\frac{x-x_{k}}{x_{{k+1}}-x_{k}}&&x\in[x_{k},x_{{k+1}}].\end{array}\right.](wyklady/nrr/mi/mi1527.png) |
(11.3) |
Widzimy wykres kilku takich funkcji, por. rysunek 11.1.
Nietrudno pokazać, że ![]() jest elementem
jest elementem ![]() , i że
, i że
![]() tworzy bazę
tworzy bazę ![]() taką, że jeśli
taką, że jeśli ![]() , to
, to
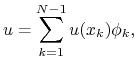 |
gdzie ![]() wartość funkcji
wartość funkcji ![]() w punkcie nodalnym
w punkcie nodalnym ![]() .
Wstawiając
.
Wstawiając ![]() do
(11.2) otrzymujemy następujący układ równań liniowych:
do
(11.2) otrzymujemy następujący układ równań liniowych:
| (11.4) |
z
![]() ,
,
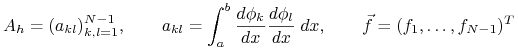 |
dla ![]() .
.
Zauważmy, że macierz ![]() jest symetryczna i trójdiagonalna. Można wykazać, że jest dodatnio określona, więc można powyższy układ rozwiązać metodą przeganiania lub odpowiednim wariantem metody Choleskiego kosztem rzędu
jest symetryczna i trójdiagonalna. Można wykazać, że jest dodatnio określona, więc można powyższy układ rozwiązać metodą przeganiania lub odpowiednim wariantem metody Choleskiego kosztem rzędu ![]() dla stałej
dla stałej ![]() niezależnej od
niezależnej od ![]() .
.
11.1.3. Zbieżność
Zastanówmy się nad zbieżnością ![]() do rozwiązania
do rozwiązania ![]() .
Najpierw trzeba ustalić w jakiej normie chcemy wykazać zbieżność.
.
Najpierw trzeba ustalić w jakiej normie chcemy wykazać zbieżność.
Naturalną normą jest norma energetyczna związana z formą dwuliniową w słabym sformułowaniu (11.1):
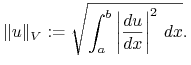 |
Wprowadzając oznaczenie ![]() i odejmując (11.2) od (11.1) otrzymujemy:
i odejmując (11.2) od (11.1) otrzymujemy:
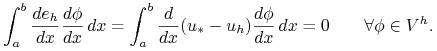 |
Następnie dla dowolnego ![]() widzimy, że
widzimy, że
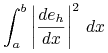 |
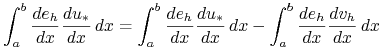 |
|||
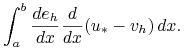 |
Korzystając z nierówności Schwarza w ![]() otrzymujemy:
otrzymujemy:
czyli
Przyjmując za ![]() liniowy interpolator
liniowy interpolator ![]() w punktach
nodalnych, tzn.
w punktach
nodalnych, tzn.
![]() , można wykazać:
, można wykazać:
![\left\|\frac{d^{k}}{dx^{k}}(u_{*}-I_{h}u_{*})\right\| _{{\infty,[a,b]}}\leq C_{k}h^{{2-k}}\left\|\frac{d^{2}u_{*}}{dx^{2}}\right\| _{{\infty,[a,b]}}\qquad k=0,1](wyklady/nrr/mi/mi1461.png) |
(11.5) |
dla pewnych stałych ![]() niezależnych od
niezależnych od ![]() ,
, ![]() i
i ![]() .
Dowód tego oszacowania pozostawiamy jako zadanie, wynika on wprost z oszacowań błędu interpolacji dla splajnów
liniowych.
.
Dowód tego oszacowania pozostawiamy jako zadanie, wynika on wprost z oszacowań błędu interpolacji dla splajnów
liniowych.
Wtedy od razu otrzymujemy:
![\| e_{h}\| _{V}\leq\| u_{*}-I_{h}u_{*}\| _{V}\leq C_{1}h\left\|\frac{d^{2}u_{*}}{dx^{2}}\right\| _{{\infty,[a,b]}},](wyklady/nrr/mi/mi1510.png) |
czyli dla funkcji klasy ![]() błąd w normie energetycznej zachowuje się jak
błąd w normie energetycznej zachowuje się jak ![]() .
.
Można też wykazać, że w normie ![]() zachodzi:
zachodzi:
![\| e_{h}\| _{{L^{2}(a,b)}}\leq Ch^{2}\left\|\frac{d^{2}u_{*}}{dx^{2}}\right\| _{{\infty,[a,b]}},](wyklady/nrr/mi/mi1518.png) |
czyli błąd zachowuje się jako ![]() - co nie jest oczywiste.
- co nie jest oczywiste.
Porównajmy to oszacowanie z oszacowaniem błędu z metody różnic skończonych (MRS)
na siatce równomiernej dla tego samego zadania różniczkowego.
Można pokazać wtedy zbieżność dyskretną
![]() w dyskretnej normie
w dyskretnej normie ![]() , por. (10.4), która w przybliżeniu odpowiada normie
, por. (10.4), która w przybliżeniu odpowiada normie ![]() ,
czyli możemy powiedzieć, że szybkość zbieżności w tym przypadku metody elementu skończonego i metody różnic skończonych jest tego samego rzędu. Ale w MRS musieliśmy założyć równomierność siatki i wyższą gładkość rozwiązania (
,
czyli możemy powiedzieć, że szybkość zbieżności w tym przypadku metody elementu skończonego i metody różnic skończonych jest tego samego rzędu. Ale w MRS musieliśmy założyć równomierność siatki i wyższą gładkość rozwiązania (![]() ).
).
11.1.4. Inne przestrzenie elementu skończonego
Przestrzeń dyskretną ![]() można też zdefiniować inaczej.
można też zdefiniować inaczej.
Dla danego podziału ![]() zdefiniujemy następujące przestrzenie elementu skończonego
dla dowolnego
zdefiniujemy następujące przestrzenie elementu skończonego
dla dowolnego ![]() :
:
gdzie ![]() jest przestrzenią wielomianów stopnia nie przekraczającego
jest przestrzenią wielomianów stopnia nie przekraczającego ![]() .
.
Widzimy, że ![]() . Przestrzeń
. Przestrzeń
![]() nazywamy przestrzenią elementu skończonego funkcji ciągłych kawałkami kwadratowych,
a przestrzeń
nazywamy przestrzenią elementu skończonego funkcji ciągłych kawałkami kwadratowych,
a przestrzeń ![]() - przestrzenią elementu skończonego funkcji ciągłych kawałkami kubicznych, czy inaczej - metodą elementu skończonego typu Lagrange'a kwadratową lub kubiczną.
Możemy teraz postawić zadanie dyskretne, jak poprzednio, tzn. szukamy
- przestrzenią elementu skończonego funkcji ciągłych kawałkami kubicznych, czy inaczej - metodą elementu skończonego typu Lagrange'a kwadratową lub kubiczną.
Możemy teraz postawić zadanie dyskretne, jak poprzednio, tzn. szukamy ![]() takiego, że
takiego, że
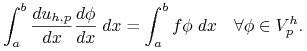 |
(11.6) |
Zadanie to ma jednoznaczne rozwiązanie. Analogicznie jak dla elementu liniowego
możemy wprowadzić tu tzw. bazę nodalną w ![]() .
Wprowadzamy dodatkowe punkty wewnątrz odcinka
.
Wprowadzamy dodatkowe punkty wewnątrz odcinka ![]() dla
dla ![]() :
:
Oczywiście ![]() .
.
Dla każdego punktu
![]() oprócz
oprócz ![]() wprowadzamy funkcję bazową
wprowadzamy funkcję bazową ![]() taką, że
taką, że
| (11.7) |
Można pokazać, że ![]() jest bazą i to taką, że
jest bazą i to taką, że
Powstaje pytanie: po co stosować przestrzenie ![]() dla
dla ![]() ?
?
Jeśli rozwiązanie ![]() jest bardziej regularne, tzn. należy do
jest bardziej regularne, tzn. należy do
![]() to można wykazać, że dla
to można wykazać, że dla ![]() :
:
![\left\|\frac{d^{k}}{dx^{k}}(u_{*}-I_{{h,p}}u_{*})\right\| _{{\infty,[a,b]}}\leq C_{k}h^{{p+1-k}}\left\|\frac{d^{{p+1}}u_{*}}{dx^{{p+1}}}\right\| _{{\infty,[a,b]}}\qquad k=0,1](wyklady/nrr/mi/mi1547.png) |
(11.8) |
i stąd, jak poprzednio dla elementu liniowego, otrzymujemy, że
![\| u_{*}-u_{{h,p}}\| _{V}\leq C_{p}h^{p}\left\|\frac{d^{{p+1}}u_{*}}{dx^{{p+1}}}\right\| _{{\infty,[a,b]}},](wyklady/nrr/mi/mi1494.png) |
(11.9) |
czyli błąd zachowuje się jak ![]() co oznacza, że w tej normie zachodzi zbieżność
rzędu
co oznacza, że w tej normie zachodzi zbieżność
rzędu ![]() .
.
11.2. Zadania
Ćwiczenie 11.1
Pokaż, że ![]() zdefiniowana w (11.3) jest
w
zdefiniowana w (11.3) jest
w ![]() , i że
, i że ![]() tworzy bazę
tworzy bazę ![]() .
.
Ćwiczenie 11.2
Wykaż (11.4).
Policz wszystkie różne od zera elementy macierzy ![]() układu (11.4).
Pokaż, że dla
układu (11.4).
Pokaż, że dla ![]() i równomiernego podziału odcinka tzn.
i równomiernego podziału odcinka tzn. ![]() macierz ta jest równa macierzy dyskretyzacji metodą różnic skończonych dla tego samego zadania, pomnożonej przez parametr
macierz ta jest równa macierzy dyskretyzacji metodą różnic skończonych dla tego samego zadania, pomnożonej przez parametr ![]() , tzn. jest macierzą układu równań liniowych (7.7). Czy oba układy równań liniowych po przeskalowaniu przez
, tzn. jest macierzą układu równań liniowych (7.7). Czy oba układy równań liniowych po przeskalowaniu przez ![]() (7.7) są wtedy identyczne?
(7.7) są wtedy identyczne?
Ćwiczenie 11.3
Pokaż, że macierz ![]() w (11.4) jest zawsze trójdiagonalna, symetryczna i dodatnio określona.
w (11.4) jest zawsze trójdiagonalna, symetryczna i dodatnio określona.
Pokaż, że dla dowolnych funkcji ![]() zachodzi
zachodzi
![]() , dla
, dla
![]() .
.
Ćwiczenie 11.4
Zaproponuj metodę rozwiązywania układu równań (11.4) będącą odpowiednią wersją metody eliminacji Gaussa dla macierzy symetrycznej trójdiagonalnej
dodatnio określonej, której koszt wynosi ![]() .
.
Ćwiczenie 11.5 (laboratoryjne)
Dla podziału równomiernego na odcinku ![]() rozwiąż w octavie (11.4)
dla znanego rozwiązania
rozwiąż w octavie (11.4)
dla znanego rozwiązania ![]() , czyli dla
, czyli dla ![]() . Prawą stronę możemy policzyć odpowiednią funkcją octave'a.
Policz rozwiązania dyskretne dla
. Prawą stronę możemy policzyć odpowiednią funkcją octave'a.
Policz rozwiązania dyskretne dla ![]() i
i ![]() . Następnie
policz normy dyskretne maksimum dla błędów
. Następnie
policz normy dyskretne maksimum dla błędów ![]() i
i ![]() (czyli maksima błędów w punktach nodalnych) i ich stosunek. (Zakładając, że błąd dla
(czyli maksima błędów w punktach nodalnych) i ich stosunek. (Zakładając, że błąd dla ![]() wynosi
wynosi ![]() , stosunek ten powinien w przybliżeniu wynosić
, stosunek ten powinien w przybliżeniu wynosić ![]() ).
).
Ćwiczenie 11.6 (częściowo laboratoryjne)
Udowodnij, że ![]() z (11.7) są w
z (11.7) są w ![]() , i że stanowią bazę tej przestrzeni. Wyprowadź bezpośrednie wzory na
, i że stanowią bazę tej przestrzeni. Wyprowadź bezpośrednie wzory na ![]() .
Narysuj w octave wykresy wszystkich
.
Narysuj w octave wykresy wszystkich ![]() na odcinku
na odcinku ![]() dla
dla ![]() ,
, ![]() i
i ![]() przy użyciu funkcji octave'a
przy użyciu funkcji octave'a
plot().
Dowód przebiega identycznie jak w przypadku ![]() , tzn. liniowego elementu skończonego.
, tzn. liniowego elementu skończonego.
Ćwiczenie 11.8
Udowodnij jednowymiarową nierówność Friedrichsa, a mianowicie, że
jeśli ![]() jest funkcją ciągłą kawałkami klasy
jest funkcją ciągłą kawałkami klasy ![]() na
na ![]() i
i ![]() ,
to
,
to
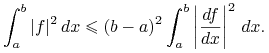 |
Ćwiczenie 11.9
Pokaż, że ![]() jest iloczynem skalarnym na
jest iloczynem skalarnym na
![]() i - ogólniej na dowolnej przestrzeni funkcyjnej zawartej
w przestrzeni funkcji ciągłych kawałkami
i - ogólniej na dowolnej przestrzeni funkcyjnej zawartej
w przestrzeni funkcji ciągłych kawałkami ![]() zerujących się w końcach odcinka
zerujących się w końcach odcinka ![]() .
W szczególności
.
W szczególności ![]() jest normą na
jest normą na ![]() .
.
Ćwiczenie 11.10
Wyprowadź układ równań liniowych
którego rozwiązaniem jest wektor współczynników w bazie
![]() , por. (11.7), rozwiązania
, por. (11.7), rozwiązania ![]() zadania (11.6). Określ ilość elementów różnych od zera w macierzy, czy
przy odpowiednim porządku indeksów funkcji bazy ta macierz może być jest pasmowa?
Jeśli tak, to znajdź wielkość pasma.
Czy jest symetryczna i dodatnio określona? Zaproponuj algorytm bezpośredni rozwiązywania tego układu kosztem
zadania (11.6). Określ ilość elementów różnych od zera w macierzy, czy
przy odpowiednim porządku indeksów funkcji bazy ta macierz może być jest pasmowa?
Jeśli tak, to znajdź wielkość pasma.
Czy jest symetryczna i dodatnio określona? Zaproponuj algorytm bezpośredni rozwiązywania tego układu kosztem ![]() , dla
, dla ![]() wymiaru
wymiaru ![]() .
.
Ćwiczenie 11.11
Udowodnij (11.5).
Ćwiczenie 11.12
Udowodnij (11.8).