Zagadnienia
12. Metoda elementu skończonego - wprowadzenia cd. Przypadek dwuwymiarowy.
W tym rozdziale przedstawimy kilka możliwie prostych dyskretyzacji skonstruowanych za pomocą metody elementu skończonego na przykładzie modelowego zadania eliptycznego na kwadracie.
12.1. Metoda elementu skończonego na kwadracie jednostkowym
Słabe sformułowanie zadania (7.8):
chcemy znaleźć ![]() takie, że
takie, że
| (12.1) |
Tutaj ![]() jest odpowiednio dobraną przestrzenią funkcji
ciągłych zerujących się na brzegu, dla których obie strony słabego sformułowania mają sens.
Np. możemy wziąć domknięcie w odpowiedniej normie przestrzeni funkcji ciągłych zerujących się na brzegu, których
słaba pochodna (pochodna w sensie dystrybucyjnym) jest w
jest odpowiednio dobraną przestrzenią funkcji
ciągłych zerujących się na brzegu, dla których obie strony słabego sformułowania mają sens.
Np. możemy wziąć domknięcie w odpowiedniej normie przestrzeni funkcji ciągłych zerujących się na brzegu, których
słaba pochodna (pochodna w sensie dystrybucyjnym) jest w ![]() .
Później precyzyjniej ustalimy o jaką przestrzeń chodzi.
.
Później precyzyjniej ustalimy o jaką przestrzeń chodzi.
Jeśli problem (12.1) ma rozwiązanie dostatecznie gładkie, tzn. ![]() posiada ciągłe pierwsze i drugie pochodne cząstkowe, to
posiada ciągłe pierwsze i drugie pochodne cząstkowe, to ![]() jest rozwiązaniem wyjściowego zadania. Może się zdarzyć, że
istnieje rozwiązanie (12.1), które nie jest nawet ciągłe.
jest rozwiązaniem wyjściowego zadania. Może się zdarzyć, że
istnieje rozwiązanie (12.1), które nie jest nawet ciągłe.
12.1.1. Triangulacja obszaru
Wprowadźmy podział (triangulacje) kwadratu ![]() na trójkąty
na trójkąty ![]() o jednakowym kształcie i wielkości. Najprościej
jest podzielić kwadrat na równe kwadraty
o jednakowym kształcie i wielkości. Najprościej
jest podzielić kwadrat na równe kwadraty ![]() dla
dla ![]() i
i ![]() dla
dla ![]() . Następnie każdy kwadrat dzielimy na
dwa trójkąty prowadząc przekątną np. z lewego górnego rogu do dolnego prawego, por. rysunek 12.1.
. Następnie każdy kwadrat dzielimy na
dwa trójkąty prowadząc przekątną np. z lewego górnego rogu do dolnego prawego, por. rysunek 12.1.
Zauważmy, że ![]() i
i
![]() jest zbiorem pustym, krawędzią lub wspólnym wierzchołkiem dla dowolnych różnych elementów tej triangulacji.
jest zbiorem pustym, krawędzią lub wspólnym wierzchołkiem dla dowolnych różnych elementów tej triangulacji.
Za parametr tej dyskretyzacji przyjmujemy ![]() , a punkty
, a punkty ![]() nazwiemy punktami nodalnymi tej triangulacji.
Proszę zauważyć, że to nie jest tylko jedna możliwa triangulacja kwadratu.
Możemy wybierać trójkąty na wiele sposobów tak, aby tylko zachowane zostały warunki, że
trójkąty są rozłączne, suma ich domknięć tworzy cały kwadrat, ich wspólne części brzegów to
wierzchołek, wspólna krawędź lub zbiór pusty.
nazwiemy punktami nodalnymi tej triangulacji.
Proszę zauważyć, że to nie jest tylko jedna możliwa triangulacja kwadratu.
Możemy wybierać trójkąty na wiele sposobów tak, aby tylko zachowane zostały warunki, że
trójkąty są rozłączne, suma ich domknięć tworzy cały kwadrat, ich wspólne części brzegów to
wierzchołek, wspólna krawędź lub zbiór pusty.
Rozpatrujemy w ogólności rodzinę takich triangulacji z ![]() .
.
12.1.2. Element liniowy
Możemy wprowadzić przestrzeń dyskretną:
dla ![]() przestrzeni wielomianów liniowych na
przestrzeni wielomianów liniowych na ![]() .
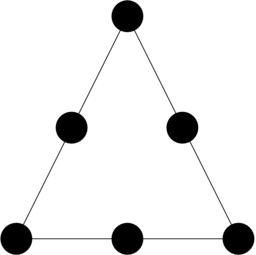
Wielomian liniowy na trójkącie jest zdefiniowany poprzez wartości w wierzchołkach tego trójkąta, które nazywamy punktami swobody tego elementu skończonego,
por. rysunek 12.2.
.
Wielomian liniowy na trójkącie jest zdefiniowany poprzez wartości w wierzchołkach tego trójkąta, które nazywamy punktami swobody tego elementu skończonego,
por. rysunek 12.2.
Analogicznie jak w przypadku jednowymiarowym, możemy wprowadzić funkcje nodalne:
definiujemy ![]() dla
dla ![]() jako funkcję, która spełnia
jako funkcję, która spełnia ![]() i
i ![]() dla
dla ![]() dla
dla ![]() .
.
W przypadku naszej
prostej regularnej triangulacji możemy wyznaczyć wzory na te funkcje na trójkącie ![]() .
Powiedzmy, że wzory wyznaczymy na tym trójkącie, który jest zaznaczony na rysunku 12.1 - przyjmujemy, że
.
Powiedzmy, że wzory wyznaczymy na tym trójkącie, który jest zaznaczony na rysunku 12.1 - przyjmujemy, że ![]() jest wierzchołkiem przy kącie prostym:
jest wierzchołkiem przy kącie prostym:
| (12.2) | |||||
dla ![]() .
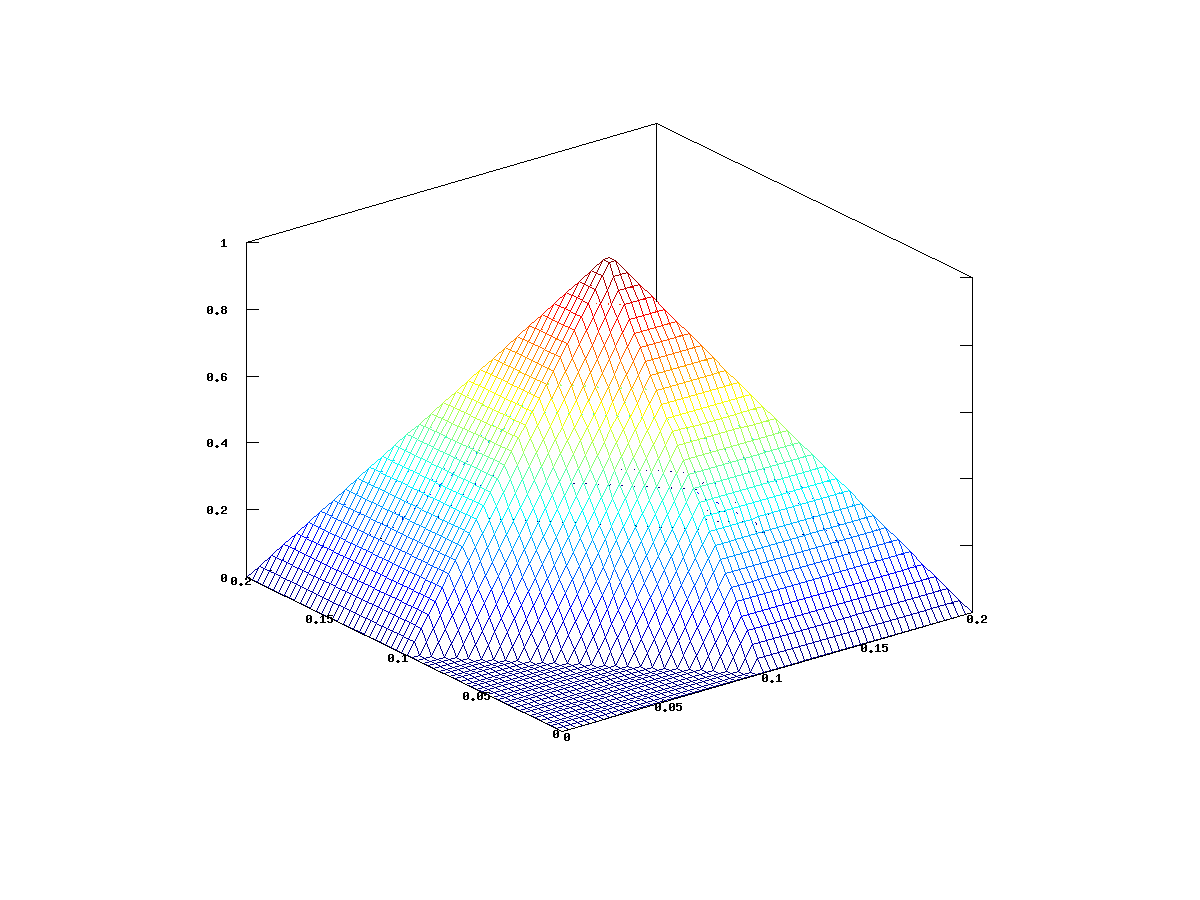
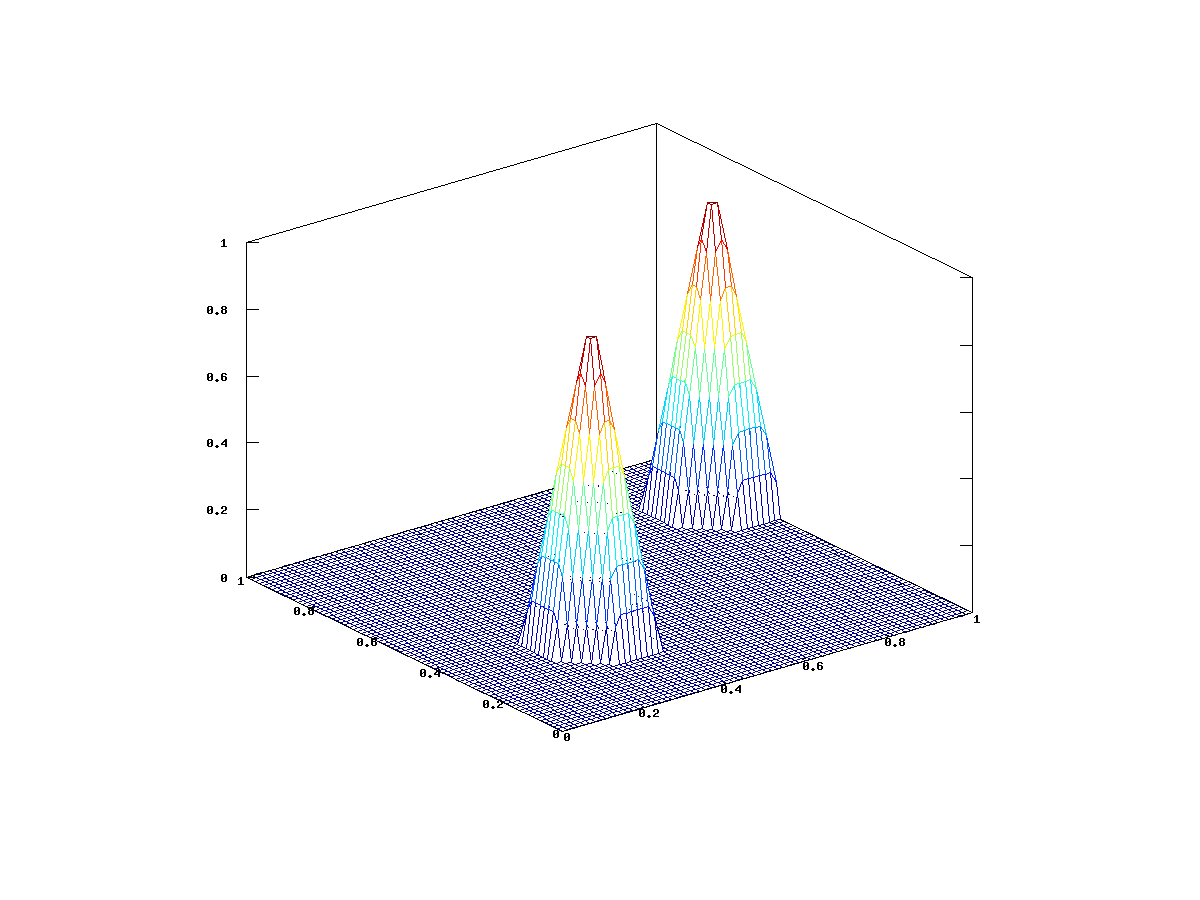
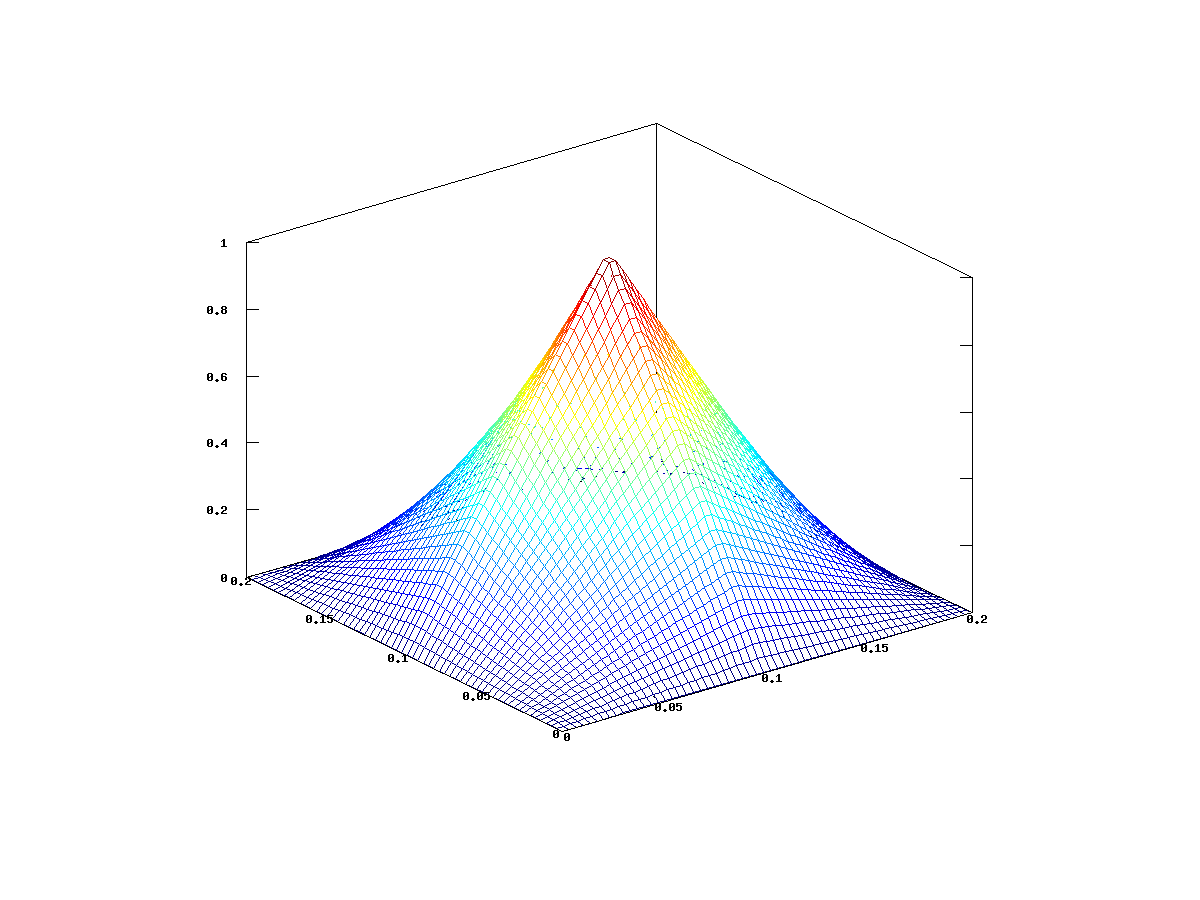
Wykresy takiej funkcji dla tej regularnej triangulacji kwadratu lub kilku funkcji
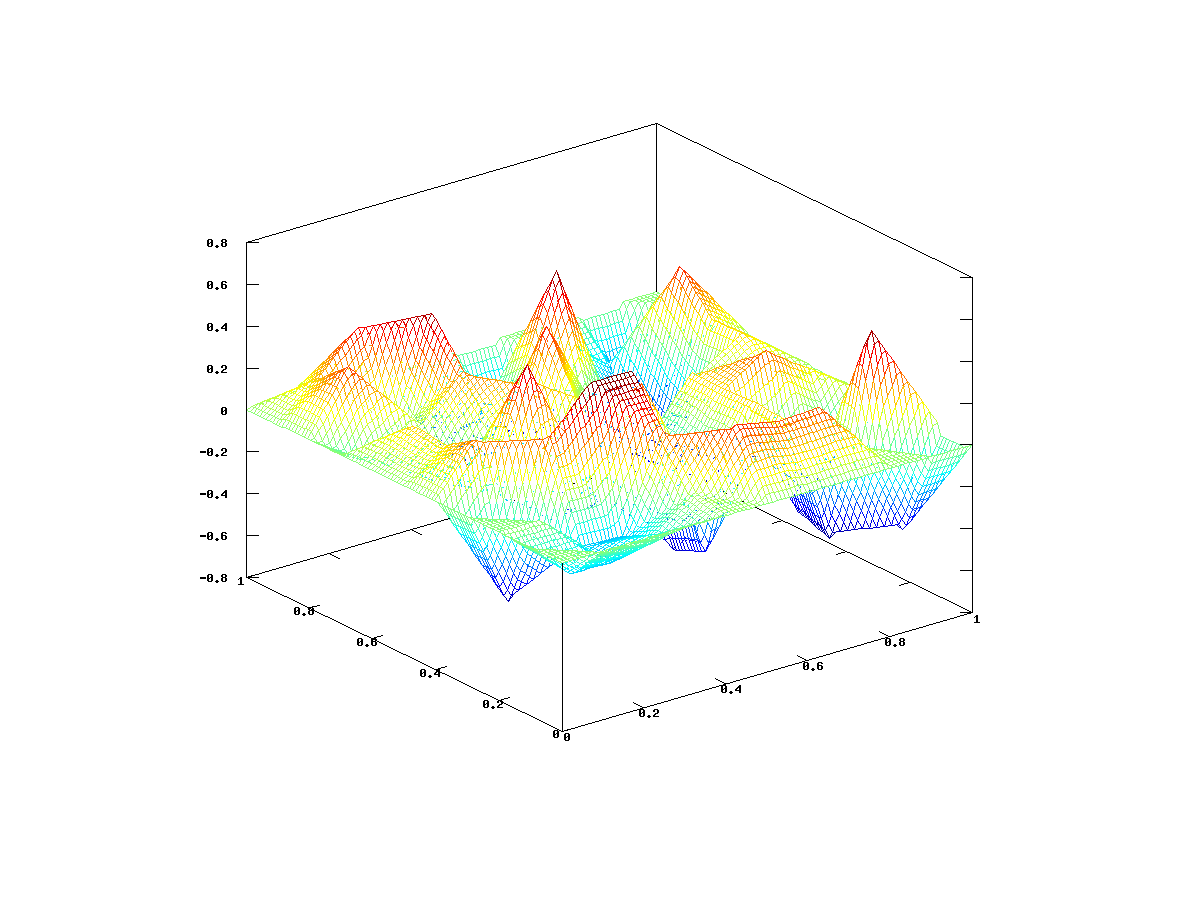
możemy obejrzeć na rysunkach 12.3 i 12.4. Na rysunku 12.5 widzimy przykładową funkcję z przestrzeni
.
Wykresy takiej funkcji dla tej regularnej triangulacji kwadratu lub kilku funkcji
możemy obejrzeć na rysunkach 12.3 i 12.4. Na rysunku 12.5 widzimy przykładową funkcję z przestrzeni ![]() .
Również jako zadanie pozostawimy wykazanie, że
.
Również jako zadanie pozostawimy wykazanie, że
tworzą bazę ![]() , i że
, i że
Wprowadzamy
zadanie dyskretne: chcemy znaleźć ![]() takie, że
takie, że
| (12.3) |
Można pokazać, że to zadanie ma jednoznaczne rozwiązanie, i że
jeśli ![]() to:
to:
| (12.4) | |||||
Zatem w normie ![]() widzimy oszacowanie zbieżności rzędu dwa analogiczne jak dla dyskretyzacji tego samego zadania przy pomocy metody różnic dzielonych i dyskretnej normy
widzimy oszacowanie zbieżności rzędu dwa analogiczne jak dla dyskretyzacji tego samego zadania przy pomocy metody różnic dzielonych i dyskretnej normy ![]() , ale przy dużo słabszych założeniach. Tam musieliśmy założyć, że funkcja jest klasy
, ale przy dużo słabszych założeniach. Tam musieliśmy założyć, że funkcja jest klasy ![]() .
.
Można też zauważyć, że w przypadku bardziej skomplikowanego geometrycznie obszaru (wielokąta) możemy skonstruować analogiczną dyskretyzację wprowadzając triangulację złożoną z trójkątów, a w przypadku różnic dzielonych, jeśli obszar nie jest prostokątem, pojawiają się kłopoty z postawieniem warunku brzegowego.
12.1.3. Element kwadratowy i kubiczny
W tym rozdziale przedstawimy dwa typy przestrzeni elementu skończonego wyższych rzędów - element kwadratowy i kubiczny.
Rozpatrzmy triangulację kwadratu jednostkowego ![]() jak w Rozdziale 12.1.1.
Wtedy definiujemy:
jak w Rozdziale 12.1.1.
Wtedy definiujemy:
dla ![]() . Tutaj
. Tutaj ![]() to przestrzeń wielomianów na
to przestrzeń wielomianów na ![]() stopnia nie większego od
stopnia nie większego od ![]() .
.
Przypadek ![]() określamy jako przestrzeń elementu skończonego kwadratowego, a
określamy jako przestrzeń elementu skończonego kwadratowego, a ![]() kubicznego.
kubicznego.
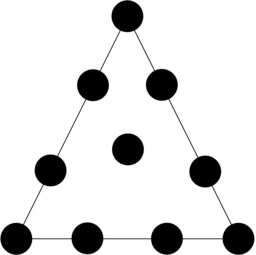
Dla ![]() widzimy, że wielomian kwadratowy na trójkącie jest określony jednoznacznie poprzez swoje wartości w trzech wierzchołkach i trzech środkach krawędzi. Wszystkie te punkty wewnątrz
widzimy, że wielomian kwadratowy na trójkącie jest określony jednoznacznie poprzez swoje wartości w trzech wierzchołkach i trzech środkach krawędzi. Wszystkie te punkty wewnątrz ![]() określamy jako punkty nodalne
określamy jako punkty nodalne ![]() . Z każdym takim punktem
. Z każdym takim punktem ![]() wiążemy funkcję, która
jest równa jeden w tym punkcie, a zero we wszystkich pozostałych wierzchołkach i punktach środkowych krawędzi, por.
rysunek 12.6.
wiążemy funkcję, która
jest równa jeden w tym punkcie, a zero we wszystkich pozostałych wierzchołkach i punktach środkowych krawędzi, por.
rysunek 12.6.
Z kolei dla ![]() wielomian kubiczny na trójkącie jest jednoznacznie określony
poprzez swoje wartości w wierzchołkach, w środku ciężkości oraz w dwu punktach wewnątrz każdej krawędzi dzielących ją na trzy równe odcinki, por. rysunek 12.7.
wielomian kubiczny na trójkącie jest jednoznacznie określony
poprzez swoje wartości w wierzchołkach, w środku ciężkości oraz w dwu punktach wewnątrz każdej krawędzi dzielących ją na trzy równe odcinki, por. rysunek 12.7.
W przypadku przestrzeni ![]() możemy wprowadzić analogiczne bazy nodalne złożone z funkcji, które przyjmują wartość jeden
w ustalonym punkcie nodalnym, a zero - w pozostałych. Wzory takich funkcji są coraz bardziej skomplikowane wraz ze wzrostem
możemy wprowadzić analogiczne bazy nodalne złożone z funkcji, które przyjmują wartość jeden
w ustalonym punkcie nodalnym, a zero - w pozostałych. Wzory takich funkcji są coraz bardziej skomplikowane wraz ze wzrostem ![]() .
Dla
.
Dla ![]() wypiszemy wzory na obcięcie funkcji nodalnej na ustalonym trójkącie
wypiszemy wzory na obcięcie funkcji nodalnej na ustalonym trójkącie ![]() .
Niech punkty
.
Niech punkty ![]()
![]() będą trzema wierzchołkami tego trójkąta
będą trzema wierzchołkami tego trójkąta ![]() i
niech punkt
i
niech punkt ![]()
![]() będzie środkiem odcinka między
będzie środkiem odcinka między ![]() a
a ![]() .
Przy czym utożsamiamy
.
Przy czym utożsamiamy ![]() z
z ![]() .
Niech
.
Niech ![]() będzie funkcją liniową taką, że
będzie funkcją liniową taką, że ![]() dla
dla ![]() i
i ![]() .
Wtedy funkcja nodalna związana z wierzchołkiem elementu
.
Wtedy funkcja nodalna związana z wierzchołkiem elementu ![]() dla elementu kwadratowego wynosi na trójkącie
dla elementu kwadratowego wynosi na trójkącie ![]() :
:
| (12.5) |
a funkcja nodalna związana z punktem środkowym krawędzi elementu na ![]() :
:
| (12.6) |
Jako zadanie pozostawiamy sprawdzenie tych wzorów i znalezienie analogicznych dla funkcji bazowych elementu kubicznego.
Zastosowanie elementów: kwadratowego (![]() ), kubicznego (
), kubicznego (![]() ) czy nawet dla większych
) czy nawet dla większych ![]() jest korzystne, o ile
jest korzystne, o ile ![]() - czyli rozwiązanie zadania różniczkowego (12.1) jest bardziej regularne, tzn. należy do
- czyli rozwiązanie zadania różniczkowego (12.1) jest bardziej regularne, tzn. należy do ![]() dla
dla ![]() większych od jeden do
większych od jeden do ![]() . Tzn. wtedy
można wykazać, że
. Tzn. wtedy
można wykazać, że
12.1.4. Metoda elementu skończonego z podziałem obszaru na prostokąty
W przypadku, gdy nasz obszar jest prostokątem lub kwadratem, możemy wprowadzić przestrzeń elementu skończonego: tzw. elementów skończonych prostokątnych.
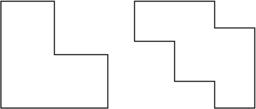
Taki element możemy w ogólności zastosować, jeśli obszar jest sumą prostokątów
o brzegach będących sumą odcinków równoległych do osi współrzędnych;
np. tzw. ![]() -obszarem, por. rysunek 12.8.
-obszarem, por. rysunek 12.8.
Opiszemy tę metodę dla naszego modelowego zadania postawionego na kwadracie.
Dla ![]() wprowadźmy triangulacje złożoną z kwadratów, por. rysunek 12.9:
wprowadźmy triangulacje złożoną z kwadratów, por. rysunek 12.9:
dla ![]() i dla kwadratów:
i dla kwadratów:
Wtedy przestrzeń dyskretną definiujemy jako przestrzeń funkcji ciągłych biliniowych na kwadratach:
gdzie
przestrzeń wielomianów biliniowych określonych na ![]() , czyli liniowych ze względu na każdą zmienną z osobna.
, czyli liniowych ze względu na każdą zmienną z osobna.
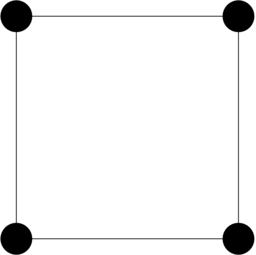
Wielomian biliniowy na prostokącie jest zdefiniowany poprzez wartości w wierzchołkach tego prostokąta. Nazywamy je punktami swobody tego elementu skończonego, por. rysunek 12.10.
Analogicznie do przypadku elementów trójkątnych możemy tu wprowadzić funkcje nodalne:
definiując ![]() dla
dla ![]() jako funkcję, która spełnia
jako funkcję, która spełnia ![]() i
i ![]() dla
dla ![]() dla
dla ![]() .
Podanie wzoru na te funkcje jest nietrudnym zadaniem z uwagi na prostą geometrię elementu. Pozostawiamy to jako zadanie, por. rysunek 12.11
.
Podanie wzoru na te funkcje jest nietrudnym zadaniem z uwagi na prostą geometrię elementu. Pozostawiamy to jako zadanie, por. rysunek 12.11
Następnie definiujemy zadanie dyskretne: chcemy
znaleźć ![]() takie, że
takie, że
| (12.7) |
W tym przypadku możemy analogicznie wykazać, że zachodzi oszacowanie błędu takie, jak w przypadku elementu liniowego na trójkącie. Tzn.
można wykazać, że to zadanie ma jednoznaczne rozwiązanie, i że
jeśli ![]() , to
, to
| (12.8) | |||||
W przypadku zadania na kwadracie jednostkowym element biliniowy wydaje się bardziej naturalny, ale przestrzeń elementu skończonego jest bardziej skomplikowana, ponieważ na każdym kwadracie triangulacji lokalna przestrzeń MESu zawiera wielomiany wyższego stopnia.
Czy możemy uzyskać lepsze oszacowania błędu? Nie -
jeśli chodzi o rząd zbieżności, tzn. dla elementu biliniowego otrzymamy co najwyżej ![]() w normie
w normie ![]() , ale
oszacowanie błędu jest ostrzejsze,
por. rozdział 4.6 w [4].
, ale
oszacowanie błędu jest ostrzejsze,
por. rozdział 4.6 w [4].
12.2. Niejednorodny warunek brzegowy
Można się zastanowić co się dzieje, jeśli w (7.8) w warunku brzegowym Dirichleta wartość prawej strony jest różna od zera, tzn. ![]() na brzegu.
Tak jak poprzednio, otrzymujemy nowe słabe sformułowanie: chcemy znaleźć
na brzegu.
Tak jak poprzednio, otrzymujemy nowe słabe sformułowanie: chcemy znaleźć ![]() takie, że
takie, że
![]() na brzegu
na brzegu ![]() spełniające (12.1).
Jeśli założymy, że znamy funkcję
spełniające (12.1).
Jeśli założymy, że znamy funkcję ![]() określoną na
określoną na ![]() taką, że
taką, że
![]() na brzegu, to definiując
na brzegu, to definiując ![]() otrzymujemy:
otrzymujemy:
dla ![]() jak w (12.1) i
jak w (12.1) i ![]() , czyli (12.1) ale z prawą stroną zależną dodatkowo od
, czyli (12.1) ale z prawą stroną zależną dodatkowo od ![]() .
.
Następnie możemy wprowadzić zadanie dyskretne tak, jak dla zerowych warunków brzegowych.
12.3. Zadania
Ćwiczenie 12.1
Udowodnij, że funkcja bazowa przestrzeni elementu liniowego na trójkącie spełnia wzory (12.1.2).
Ćwiczenie 12.2
Definiujemy rozwiązanie (12.1) jako
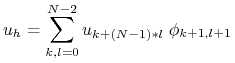 |
z ![]() .
Wstawiając
.
Wstawiając ![]() w tej postaci do (12.1) otrzymujemy układ równań liniowych na
wektor współrzędnych
w tej postaci do (12.1) otrzymujemy układ równań liniowych na
wektor współrzędnych ![]() .
Policz różne od zera elementy macierzy tego układu
.
Policz różne od zera elementy macierzy tego układu ![]() i elementy wektora prawej strony
i elementy wektora prawej strony ![]() . Czy elementy na diagonali tej macierzy zależą od
. Czy elementy na diagonali tej macierzy zależą od ![]() ?
Pokaż, że dla równomiernego podziału, tzn.
?
Pokaż, że dla równomiernego podziału, tzn. ![]() , macierz ta jest równa macierzy dyskretyzacji metodą różnic skończonych dla tego samego zadania, pomnożonej przez parametr
, macierz ta jest równa macierzy dyskretyzacji metodą różnic skończonych dla tego samego zadania, pomnożonej przez parametr ![]() , tzn. macierzą układu równań liniowych dla ćwiczenia 7.5 (dla
, tzn. macierzą układu równań liniowych dla ćwiczenia 7.5 (dla ![]() ). Czy oba układy po przeskalowaniu przez
). Czy oba układy po przeskalowaniu przez ![]() są wtedy identyczne?
są wtedy identyczne?
Układy równań liniowych nie są identyczne, ponieważ prawe strony są różne, tak jak w przypadku jednowymiarowym.
Ćwiczenie 12.3
Pokaż, że macierz ![]() z ćwiczenia 12.2 jest zawsze pasmowa (wyznacz wielkość pasma, wyznacz czy zależy ono od
z ćwiczenia 12.2 jest zawsze pasmowa (wyznacz wielkość pasma, wyznacz czy zależy ono od ![]() , czyli odpowiednio od
, czyli odpowiednio od ![]() ), symetryczna i dodatnio określona.
), symetryczna i dodatnio określona.
Ćwiczenie 12.4
Zakładając, że posiadamy procedurę z metodą iteracyjną, która rozwiązuje układ równań z ćwiczenia 12.2 w ![]() iteracji,
i dla której w każdej iteracji wykonujemy jedno mnożenie przez macierz
iteracji,
i dla której w każdej iteracji wykonujemy jedno mnożenie przez macierz ![]() oraz
oraz ![]() operacji algebraicznych
określ, ile musi wynosić
operacji algebraicznych
określ, ile musi wynosić ![]() , aby metoda ta była tańsza od odpowiedniej taśmowej
wersji eliminacji Gaussa dla macierzy symetrycznej dodatnio określonej.
, aby metoda ta była tańsza od odpowiedniej taśmowej
wersji eliminacji Gaussa dla macierzy symetrycznej dodatnio określonej.
Ćwiczenie 12.5
Pokaż, że dla dowolnej funkcji przestrzeni liniowej elementu skończonego ![]() , por. rozdział 12.1.2, zachodzi tzw. nierówność odwrotna:
, por. rozdział 12.1.2, zachodzi tzw. nierówność odwrotna:
Tutaj stała ![]() jest niezależna od parametru
jest niezależna od parametru ![]() i
i ![]() .
.
Wystarczy pokazać to oszacowanie na dowolnym elemencie triangulacji ![]() i wykorzystać fakt, że
i wykorzystać fakt, że ![]() dla dowolnej stałej
dla dowolnej stałej ![]() .
.
Ćwiczenie 12.6
(laboratoryjne)
Napisz w octave odpowiednią wersję
eliminacji Gaussa dla macierzy pasmowej symetrycznej dodatnio określonej. Zastosuj ją do układu równań liniowych z ćwiczenia 12.2 dla ![]() różnej wielkości. Porównaj czas w octavie
z czasem dla standardowej metody rozwiązywania równań liniowych octave'a zarówno, gdy macierz układu jest w formacie pełnym, jak i formacie rzadkim (można użyć funkcje octave:
różnej wielkości. Porównaj czas w octavie
z czasem dla standardowej metody rozwiązywania równań liniowych octave'a zarówno, gdy macierz układu jest w formacie pełnym, jak i formacie rzadkim (można użyć funkcje octave: sparse(),
tic() i toc() i operator octave: \).
Ćwiczenie 12.7
Udowodnij, że funkcja z ![]() jest jednoznacznie wyznaczona przez określenie jej wartości
w wierzchołkach i środkach krawędzi trójkąta (jak opisano w rozdziale 12.1.3, por. rysunek 12.6).
jest jednoznacznie wyznaczona przez określenie jej wartości
w wierzchołkach i środkach krawędzi trójkąta (jak opisano w rozdziale 12.1.3, por. rysunek 12.6).
Ćwiczenie 12.8
Udowodnij, że funkcja z ![]() jest jednoznacznie wyznaczona przez określenie jej wartości
jak opisano w rozdziale 12.1.3, por. rysunek 12.7.
jest jednoznacznie wyznaczona przez określenie jej wartości
jak opisano w rozdziale 12.1.3, por. rysunek 12.7.
Ćwiczenie 12.9
Dla przestrzeni ![]() wyprowadź układ równań liniowych:
wyprowadź układ równań liniowych:
taki, że
jego rozwiązaniem są współczynniki rozwiązania przybliżonego ![]() w bazie
nodalnej tej przestrzeni elementu skończonego, por. rozdział 12.1.3.
Czy macierz tego układu jest pasmowa? Jeśli tak, to znajdź wielkość pasma.
Czy jest symetryczna i dodatnio określona?
w bazie
nodalnej tej przestrzeni elementu skończonego, por. rozdział 12.1.3.
Czy macierz tego układu jest pasmowa? Jeśli tak, to znajdź wielkość pasma.
Czy jest symetryczna i dodatnio określona?
Ćwiczenie 12.10
Udowodnij wzory na bazowe funkcje elementu kwadratowego na trójkącie (12.5) i (12.6).
Ćwiczenie 12.11
Wyznacz wzory na bazowe funkcje nodalne dla elementu kubicznego, analogiczne
do wzorów (12.5) i (12.6) dla funkcji bazowych elementu kwadratowego, tzn. wzory na te funkcje w zależności od funkcji ![]() .
.
Ćwiczenie 12.12
Wyznacz wzory na współczynniki bazowych funkcji nodalnych dla elementu biliniowego na kwadracie
![]() w bazie
w bazie ![]() .
Oblicz elementy macierzy układu równań liniowych dla dyskretyzacji metodą elementu skończonego biliniowego dla zadania dyskretnego
(12.7) w tej bazie nodalnej.
.
Oblicz elementy macierzy układu równań liniowych dla dyskretyzacji metodą elementu skończonego biliniowego dla zadania dyskretnego
(12.7) w tej bazie nodalnej.
Ćwiczenie 12.13
Dla przestrzeni ![]() , wyprowadź układ równań liniowych:
, wyprowadź układ równań liniowych:
taki, że
jego rozwiązaniem są współczynniki rozwiązania przybliżonego ![]() w bazie
nodalnej związanej z wierzchołkami elementów kwadratowych.
Czy macierz tego układu jest pasmowa? Jeśli tak, to znajdź wielkość pasma.
Czy jest symetryczna i dodatnio określona?
w bazie
nodalnej związanej z wierzchołkami elementów kwadratowych.
Czy macierz tego układu jest pasmowa? Jeśli tak, to znajdź wielkość pasma.
Czy jest symetryczna i dodatnio określona?