Zagadnienia
- 13.1 Istnienie rozwiązania
- 13.2 Metoda Galerkina
- 13.3 Abstrakcyjne oszacowanie błędu
- 13.4 Przestrzenie Sobolewa
- 13.5 Zadanie eliptyczne drugiego rzędu z zerowymi warunkami na brzegu
- 13.6 Ciągła metoda elementu skończonego dla zadań eliptycznych drugiego rzędu
- 13.7 Zadania dyskretne i zbieżność
- 13.8 Zadania
13. Metoda elementu skończonego - teoria
W tym wykładzie przedstawimy ogólną teorię konstrukcji i analizy zbieżności elementu skończonego (MESu) dla równań liniowych.
13.1. Istnienie rozwiązania
Załóżmy, że ![]() jest rzeczywistą przestrzenią Hilberta, tzn. rzeczywistą przestrzenią liniową
z iloczynem skalarnym
jest rzeczywistą przestrzenią Hilberta, tzn. rzeczywistą przestrzenią liniową
z iloczynem skalarnym ![]() i normą
i normą ![]() , która jest zupełna. Przez
, która jest zupełna. Przez ![]() oznaczamy przestrzeń dualną (sprzężoną) do
oznaczamy przestrzeń dualną (sprzężoną) do ![]() ,
por. np. [7].
,
por. np. [7].
Rozpatrzmy wariacyjny problem znalezienia ![]() takiego, że
takiego, że
| (13.1) |
gdzie ![]() ,
, ![]() jest formą dwuliniową, która jest ograniczona, tzn. istnieje stała
jest formą dwuliniową, która jest ograniczona, tzn. istnieje stała
![]() taka, że
taka, że
oraz jest ![]() -eliptyczna co oznacza, że dla pewnego
-eliptyczna co oznacza, że dla pewnego ![]() zachodzi:
zachodzi:
Przy powyższych założeniach zachodzi znane twierdzenie analizy funkcjonalnej:
Twierdzenie 13.1 (Lax-Milgram)
Rozpatrzmy formę dwuliniową ![]() , która jest
ograniczona i
, która jest
ograniczona i ![]() -eliptyczna, a
-eliptyczna, a ![]() . Wtedy zadanie
(13.1) ma jednoznaczne rozwiązanie i
. Wtedy zadanie
(13.1) ma jednoznaczne rozwiązanie i
| (13.2) |
Istnienie rozwiązania wynika z lematu Riesza. Szczegóły dowodu można znaleźć
np. w [7] lub [6].
Oszacowanie (13.2) dla ![]() otrzymujemy wstawiając
otrzymujemy wstawiając ![]() za
za ![]() w (13.1) i korzystając z
w (13.1) i korzystając z ![]() -eliptyczności formy i definicji normy dualnej funkcjonału liniowego:
-eliptyczności formy i definicji normy dualnej funkcjonału liniowego:
Jeśli ![]() i
i ![]() są rozwiązaniami zadania wariacyjnego, to
są rozwiązaniami zadania wariacyjnego, to ![]() spełnia (13.1) dla prawej strony równej zero. Z tego i z (13.2) wynika, że
spełnia (13.1) dla prawej strony równej zero. Z tego i z (13.2) wynika, że ![]() , co oznacza, że rozwiązanie jest wyznaczone jednoznacznie.
, co oznacza, że rozwiązanie jest wyznaczone jednoznacznie.
13.2. Metoda Galerkina
Załóżmy, że ![]() to rodzina podprzestrzeni skończenie wymiarowych
to rodzina podprzestrzeni skończenie wymiarowych ![]() o wymiarze
o wymiarze ![]() .
.
Definiujemy zadanie dyskretne aproksymujące (13.1): chcemy znaleźć ![]() takie, że
takie, że
| (13.3) |
Forma ![]() jest ograniczona na
jest ograniczona na ![]() z normą przestrzeni
z normą przestrzeni ![]() i jest również
i jest również ![]() -eliptyczna. Zatem z twierdzenia 13.1
wynika istnienie jednoznacznego rozwiązania
zadania dyskretnego, które spełnia:
-eliptyczna. Zatem z twierdzenia 13.1
wynika istnienie jednoznacznego rozwiązania
zadania dyskretnego, które spełnia:
| (13.4) |
Rozwiązania dyskretne są wspólnie ograniczone niezależnie od wymiaru ![]() , co określamy jako stabilność rozwiązań rodziny zadań dyskretnych.
, co określamy jako stabilność rozwiązań rodziny zadań dyskretnych.
Proszę zauważyć, że ponieważ przestrzeń ![]() jest skończenie wymiarowa, więc - z definicji - ma bazę o skończonej ilości elementów
jest skończenie wymiarowa, więc - z definicji - ma bazę o skończonej ilości elementów ![]() , tzn.
, tzn. ![]() i, aby znaleźć współczynniki rozwiązania (13.3)
w tej bazie, należy rozwiązać układ równań liniowych
i, aby znaleźć współczynniki rozwiązania (13.3)
w tej bazie, należy rozwiązać układ równań liniowych
gdzie ![]() i
i ![]() dla
dla ![]() .
Jeśli forma
.
Jeśli forma ![]() jest symetryczna, to
jest symetryczna, to ![]() jest macierzą symetryczną i dodatnio określoną.
Oczywiście najlepiej byłoby dobrać taką bazę, żeby macierz
jest macierzą symetryczną i dodatnio określoną.
Oczywiście najlepiej byłoby dobrać taką bazę, żeby macierz ![]() była np. pasmowa, albo ogólniej - o małej ilości elementów różnych od zera.
Pojawia się pytanie: jak taką bazę wyznaczyć?
była np. pasmowa, albo ogólniej - o małej ilości elementów różnych od zera.
Pojawia się pytanie: jak taką bazę wyznaczyć?
13.3. Abstrakcyjne oszacowanie błędu
Tutaj pokażemy związek między błędem ![]() , a błędem aproksymacji przestrzeni
, a błędem aproksymacji przestrzeni ![]() przez rodzinę przestrzeni
przez rodzinę przestrzeni ![]() .
.
Zachodzi ważne twierdzenie - zwyczajowo zwane lematem Céa:
Twierdzenie 13.2 (lemat Céa)
Niech forma ![]() określona na przestrzeni Hilberta
określona na przestrzeni Hilberta ![]() będzie ograniczona i
będzie ograniczona i ![]() -eliptyczna,
-eliptyczna, ![]() podprzestrzeń
podprzestrzeń ![]() . Wtedy
. Wtedy
Z (13.1) wynika, że:
Odejmując to równanie od (13.3) otrzymujemy:
A dalej
Dzieląc przez ![]() otrzymujemy tezę twierdzenia.
otrzymujemy tezę twierdzenia.
Z lematu wynika, że aby oszacować błąd ![]() wystarczy oszacować błąd aproksymacji
wystarczy oszacować błąd aproksymacji ![]() przez podprzestrzeń dyskretną
przez podprzestrzeń dyskretną ![]() .
.
Wniosek 13.1
Przy założeniach lematu Céa,
jeśli rodzina podprzestrzeni ![]() przestrzeni Hilberta
przestrzeni Hilberta ![]() jest taka, że:
jest taka, że:
to
13.4. Przestrzenie Sobolewa
Niech ![]() będzie otwartym obszarem. Wtedy
definiujemy półnormę i normę
będzie otwartym obszarem. Wtedy
definiujemy półnormę i normę ![]() jako:
jako:
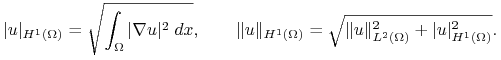 |
Dodatkowo będziemy też oznaczać ![]() i
i ![]() .
.
Definicja 13.1
Niech ![]() będzie domknięciem w normie
będzie domknięciem w normie ![]() przestrzeni
przestrzeni
![]() , gdzie
, gdzie ![]() jest podprzestrzenią
jest podprzestrzenią ![]() złożoną z funkcji o zwartym nośniku w
złożoną z funkcji o zwartym nośniku w ![]() .
.
Jest to przestrzeń zupełna (ang. complete space)
z iloczynem skalarnym ![]() :
: ![]() . Można pokazać, że jest to ośrodkowa przestrzeń Hilberta (ang. separable Hilbert space), tzn. posiada przeliczalną bazę ortonormalną (ang. countable orthonormal basis).
. Można pokazać, że jest to ośrodkowa przestrzeń Hilberta (ang. separable Hilbert space), tzn. posiada przeliczalną bazę ortonormalną (ang. countable orthonormal basis).
Pojawia się pytanie; czy jeśli funkcja ![]() ,
to
,
to ![]() .
Okazuje się, że tak jest, co wynika z twierdzenia o śladzie,
por. twierdzenie 16.2.
.
Okazuje się, że tak jest, co wynika z twierdzenia o śladzie,
por. twierdzenie 16.2.
Z nierówności Friedrichsa
(por. stwierdzenie 16.1) wynika, że półnorma ![]() w przestrzeni
w przestrzeni ![]() jest normą równoważną z normą
jest normą równoważną z normą ![]() .
.
Dodatkowo zdefiniujemy półnormę ![]() :
:
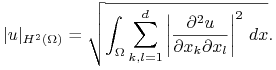 |
poprawnie zdefiniowaną dla funkcji gładkich i przestrzeń ![]() złożoną z tych funkcji w
złożoną z tych funkcji w ![]() ,
dla których jej drugie pochodne dystrybucyjne są w
,
dla których jej drugie pochodne dystrybucyjne są w ![]() . Przestrzeń ta zawiera wszystkie funkcje klasy
. Przestrzeń ta zawiera wszystkie funkcje klasy ![]() zerujące się na brzegu
zerujące się na brzegu ![]() .
.
13.5. Zadanie eliptyczne drugiego rzędu z zerowymi warunkami na brzegu
Rozpatrzmy ogólne zadanie eliptyczne w słabym sformułowaniu: chcemy znaleźć ![]() takie, że
takie, że
| (13.5) |
gdzie ![]() dla danej funkcji
dla danej funkcji ![]() oraz
oraz
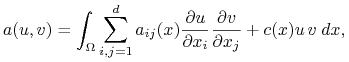 |
Tutaj funkcje ![]() , tzn. są ograniczone, oraz istnieje stała
, tzn. są ograniczone, oraz istnieje stała ![]() taka, że:
taka, że:
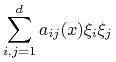 |
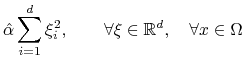 |
|||
Jeśli dodatkowo ![]() na
na ![]() to mówimy, że zadanie jest samosprzężone.
Można wykazać, że istnieją stałe dodatnie
to mówimy, że zadanie jest samosprzężone.
Można wykazać, że istnieją stałe dodatnie ![]() takie, że:
takie, że:
| (13.6) | |||||
czyli forma dwuliniowa ![]() jest ograniczona w
jest ograniczona w ![]() i
i ![]() -eliptyczna.
-eliptyczna.
Jako wniosek z twierdzenia 13.1 otrzymujemy:
Stwierdzenie 13.1
Zadanie (13.5) ma jednoznaczne rozwiązanie.
Jeśli zadanie jest samosprzężone to:
i forma ![]() jest iloczynem skalarnym w
jest iloczynem skalarnym w ![]() .
.
Można pokazać, że jeśli istnieje rozwiązanie ![]() zadania (13.5),
które dodatkowo jest klasy
zadania (13.5),
które dodatkowo jest klasy ![]() , i jeśli funkcje
, i jeśli funkcje ![]() , to
, to
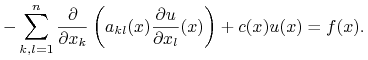 |
13.6. Ciągła metoda elementu skończonego dla zadań eliptycznych drugiego rzędu
W tym rozdziale przedstawimy ogólne zasady konstrukcji ciągłej metody elementu skończonego. Ciągłość oznacza, że przestrzenie elementu skończonego będą zawierały wyłącznie funkcje ciągłe z przestrzeni wyjściowej ![]() .
.
Będziemy zajmowali się konstrukcją przestrzeni wyłącznie dla zagadnień różniczkowych
zadanych na ograniczonym obszarze ![]() dla
dla ![]()
13.6.1. Triangulacje
Będziemy zakładali, że ![]() jest odcinkiem dla
jest odcinkiem dla ![]() , wielokątem dla
, wielokątem dla ![]() , czy wielościanem dla
, czy wielościanem dla ![]() .
.
Wprowadzamy w ![]() rodzinę podziałów
rodzinę podziałów ![]() dla
dla ![]() na odpowiednio: odcinki dla
na odpowiednio: odcinki dla ![]() , trójkąty lub prostokąty dla
, trójkąty lub prostokąty dla ![]() , czworościany lub prostopadłościany dla
, czworościany lub prostopadłościany dla ![]() - przy czym typ elementu zawsze jest ustalony.
Formalnie wprowadzamy następującą definicję triangulacji, por. rozdział 12.1.1:
- przy czym typ elementu zawsze jest ustalony.
Formalnie wprowadzamy następującą definicję triangulacji, por. rozdział 12.1.1:
Rozpatrzmy obszar ![]() ,
, ![]() będący odcinkiem, wielokątem (ang. polygon), lub wielościanem (ang. polyhedron),
i niech
będący odcinkiem, wielokątem (ang. polygon), lub wielościanem (ang. polyhedron),
i niech ![]() będzie podziałem
będzie podziałem ![]() , tzn. rodziną
wielościanów (ang. polyhedrons or elements) zazwyczaj ustalonego typu, tzn. odcinków (ang. segments) dla
, tzn. rodziną
wielościanów (ang. polyhedrons or elements) zazwyczaj ustalonego typu, tzn. odcinków (ang. segments) dla ![]() , trójkątów (ang. triangles), czworokątów (ang. quadrilaterals) lub prostokątów (ang. rectangles) dla
, trójkątów (ang. triangles), czworokątów (ang. quadrilaterals) lub prostokątów (ang. rectangles) dla ![]() , czworościanów (ang. tetrahedrons) lub prostopadłościanów (ang. cuboids) czy sześcianów (ang. cubes) dla
, czworościanów (ang. tetrahedrons) lub prostopadłościanów (ang. cuboids) czy sześcianów (ang. cubes) dla ![]() .
.
Definicja 13.2
(Triangulacja obszaru)
-
Powiemy, że
 jest dopuszczalną triangulacją (ang. admissible triangulation), jeśli spełnione są następujące warunki:
jest dopuszczalną triangulacją (ang. admissible triangulation), jeśli spełnione są następujące warunki:-
 ,
, -
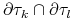 jest zbiorem pustym, wspólnym wierzchołkiem, wspólną krawędzią (
jest zbiorem pustym, wspólnym wierzchołkiem, wspólną krawędzią (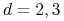 ),
wspólną ścianą (tylko
),
wspólną ścianą (tylko 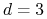 ), jeśli
), jeśli 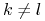 .
.
-
-
Dla danej triangulacji
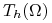 niech
niech 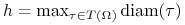 oznacza parametr tej triangulacji.
oznacza parametr tej triangulacji. -
Rodzina triangulacji
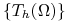 jest regularna ze względu na kształt (ang. shape regular), jeśli
istnieje stała
jest regularna ze względu na kształt (ang. shape regular), jeśli
istnieje stała 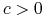 taka, że każdy
taka, że każdy 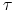 w
w 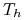 zawiera okrąg wpisany w
zawiera okrąg wpisany w 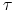 o promieniu
o promieniu 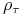 taki, że
taki, że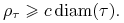
-
Rodzina triangulacji
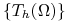 jest regularna równomiernie (ang. quasiuniform), jeśli jest regularna ze względu na kształt i
istnieje stała
jest regularna równomiernie (ang. quasiuniform), jeśli jest regularna ze względu na kształt i
istnieje stała 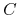 taka, że każdy
taka, że każdy 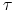 w
w 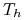 zawiera okrąg wpisany w
zawiera okrąg wpisany w 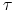 o promieniu
o promieniu 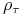 taki, że
taki, że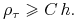
Własność regularności ze względu na kształt i własność równomiernej regularności są niezbędne w teorii zbieżności metod elementu skończonego.
Będziemy zakładali, że dla rodziny triangulacji ![]() - czyli podziałów na wielościany (ang. polyhedrons) ustalonego typu -
istnieje tzw. wielościan wzorcowy
- czyli podziałów na wielościany (ang. polyhedrons) ustalonego typu -
istnieje tzw. wielościan wzorcowy ![]() i ustalona przestrzeń wielomianów
i ustalona przestrzeń wielomianów ![]() określonych
na
określonych
na ![]() wraz z ustalonymi różnymi punktami
wraz z ustalonymi różnymi punktami ![]() takimi, że
każdy wielomian
takimi, że
każdy wielomian ![]() jest wyznaczony jednoznacznie przez swoje wartości
w tych punktach.
jest wyznaczony jednoznacznie przez swoje wartości
w tych punktach.
Definicja 13.3
Rozpatrzmy rodzinę przestrzeni funkcji ciągłych ![]() takich, że
dla triangulacji
takich, że
dla triangulacji ![]() i dowolnego
i dowolnego ![]() istnieje izomorficzne przekształcenie afiniczne
istnieje izomorficzne przekształcenie afiniczne ![]() takie, że dla dowolnej funkcji
takie, że dla dowolnej funkcji ![]() istnieje
istnieje ![]() takie, że
takie, że
Wtedy ![]() nazywamy przestrzenią ciągłego elementu skończonego (ang. continuous finite element space), a rodzinę tych przestrzeni -
afiniczną rodziną ciągłych przestrzeni elementu skończonego (ang. affine family of FE spaces).
Punkty
nazywamy przestrzenią ciągłego elementu skończonego (ang. continuous finite element space), a rodzinę tych przestrzeni -
afiniczną rodziną ciągłych przestrzeni elementu skończonego (ang. affine family of FE spaces).
Punkty ![]() nazywamy punktami nodalnymi na elemencie
nazywamy punktami nodalnymi na elemencie ![]() , a ich zbiór oznaczamy
, a ich zbiór oznaczamy ![]() , a przestrzeń wielomianów
, a przestrzeń wielomianów ![]() jest lokalną przestrzenią wielomianów na
jest lokalną przestrzenią wielomianów na ![]() .
.
Zbiór punktów nodalnych (ang. nodal points)
Dodatkowo będziemy zakładali, że dla danej przestrzeni ciągłej elementu skończonego ![]() zbudowanej na triangulacji
zbudowanej na triangulacji ![]() obszaru
obszaru ![]() istnieje
istnieje ![]() - podzbiór zbioru wszystkich punktów nodalnych wielościanów z triangulacji
- podzbiór zbioru wszystkich punktów nodalnych wielościanów z triangulacji ![]() taki, że wartości funkcji z
taki, że wartości funkcji z ![]() , zwane wartościami nodalnymi tej funkcji
w tym zbiorze, jednoznacznie tę funkcję definiują.
, zwane wartościami nodalnymi tej funkcji
w tym zbiorze, jednoznacznie tę funkcję definiują.
Wprowadzamy definicję bazy nodalnej związanej z punktami nodalnymi:
Definicja 13.4
Bazą nodalną (ang. nodal basis) związaną ze zbiorem punktów nodalnych ![]() (ang. nodal points) nazywamy układ funkcji
(ang. nodal points) nazywamy układ funkcji
![]() w
w ![]() taki, że
taki, że
.
Ten układ jest bazą w ![]() i widzimy, że:
i widzimy, że:
| (13.7) |
Wprowadzamy też pojęcie operatora interpolacji nodalnej:
Definicja 13.5
Rozpatrzmy ![]() ciągłą przestrzeń elementu skończonego, zbudowaną na triangulacji
ciągłą przestrzeń elementu skończonego, zbudowaną na triangulacji ![]() , oraz
niech
, oraz
niech ![]() będzie zbiorem punktów nodalnych dla tej przestrzeni.
Wtedy operatorem interpolacji nodalnej (ang. nodal interpolant) dla
będzie zbiorem punktów nodalnych dla tej przestrzeni.
Wtedy operatorem interpolacji nodalnej (ang. nodal interpolant) dla ![]() nazwiemy operator:
nazwiemy operator: ![]() zdefiniowany jako
zdefiniowany jako
Nietrudno zauważyć, że:
Stwierdzenie 13.2
Operator interpolacji ![]() jest rzutem na
jest rzutem na ![]() , tzn.
, tzn.
13.6.2. Warunek ciągłości, a przestrzeń Sobolewa 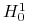
Następne twierdzenie podaje nam warunek dostateczny na to, by przestrzeń zawierająca funkcje, które na podzbiorach są odpowiednio gładkie była zawarta w ![]() .
.
Twierdzenie 13.3
Niech ![]() będzie triangulacją obszaru
będzie triangulacją obszaru ![]() . Niech
. Niech ![]() będzie taka, że
będzie taka, że ![]() i
i
![]() dla dowolnego
dla dowolnego ![]() . Wtedy
. Wtedy
![]() .
.
Dowód można znaleźć np. w [7]. Wynika z niego, że:
Wniosek 13.2
Jeśli wszystkie funkcje z ciągłej przestrzeni elementu skończonego ![]() na obszarze
na obszarze ![]() (por. definicja 13.3)
przyjmują zerowe wartości na brzegu
(por. definicja 13.3)
przyjmują zerowe wartości na brzegu ![]() ,
to
,
to ![]() jest podprzestrzenią
jest podprzestrzenią ![]() .
.
13.6.3. Aproksymacyjne własności ciągłych przestrzeni elementu skończonego w
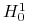
Zachodzi następujące twierdzenie o aproksymacji dla operatora interpolacji nodalnej:
Twierdzenie 13.4
Rozpatrzmy ![]() afiniczną rodzinę ciągłych przestrzeni elementu skończonego zbudowanych na dopuszczalnej rodzinie triangulacji regularnych co do kształtu taką, że
afiniczną rodzinę ciągłych przestrzeni elementu skończonego zbudowanych na dopuszczalnej rodzinie triangulacji regularnych co do kształtu taką, że ![]() , oraz
, oraz ![]() .
Wtedy dla operatora interpolacji nodalnej w przestrzeni
.
Wtedy dla operatora interpolacji nodalnej w przestrzeni ![]() zachodzi:
zachodzi:
Rozpatrzmy funkcję ciągła ![]() na elemencie
na elemencie ![]() i
i ![]() taką funkcję w
taką funkcję w ![]() , że
, że
Wtedy
co wynika wprost z definicji bazy nodalnej ![]() i operatora interpolacji
nodalnej
i operatora interpolacji
nodalnej ![]() (por. definicje 13.4 i 13.5).
Zauważmy, że twierdzenia Sobolewa o włożeniu
(ang. Sobolev embedding theorem), zob. twierdzenie 16.3,
wynika, że dla
(por. definicje 13.4 i 13.5).
Zauważmy, że twierdzenia Sobolewa o włożeniu
(ang. Sobolev embedding theorem), zob. twierdzenie 16.3,
wynika, że dla ![]() zachodzi
zachodzi ![]() .
Z twierdzenia 16.5
(biorąc
.
Z twierdzenia 16.5
(biorąc ![]() i
i ![]() )
otrzymujemy:
)
otrzymujemy:
co kończy dowód.
∎13.7. Zadania dyskretne i zbieżność
Dla rodziny triangulacji i przestrzeni ciągłych funkcji elementu skończonego ![]() , zawierających funkcje zerujące się na brzegu, możemy wprowadzić zadanie dyskretne, a dokładniej rodzinę zadań dyskretnych (13.3), które mają jednoznaczne rozwiązania i
są stabilne, tzn. wspólnie ograniczone (por. (13.4)).
, zawierających funkcje zerujące się na brzegu, możemy wprowadzić zadanie dyskretne, a dokładniej rodzinę zadań dyskretnych (13.3), które mają jednoznaczne rozwiązania i
są stabilne, tzn. wspólnie ograniczone (por. (13.4)).
Teraz możemy wykorzystać teorię ciągłego elementu skończonego, aby otrzymać zbieżność i oszacowanie błędu dla elementu liniowego, por. rozdział 12.1.2, ale również elementów wyższego rzędu:
Wniosek 13.3
Załóżmy, że spełnione są założenia twierdzenia 13.4
o rodzinie przestrzeni elementu skończonego ![]() zawartych w
zawartych w ![]() .
Rozpatrzmy
.
Rozpatrzmy ![]() rozwiązanie (13.5) i
rozwiązanie (13.5) i ![]() rozwiązanie zadania dyskretnego (13.3) z formą dwuliniową z (13.5) i przestrzenią dyskretną
rozwiązanie zadania dyskretnego (13.3) z formą dwuliniową z (13.5) i przestrzenią dyskretną ![]() .
Wtedy
.
Wtedy
a jeśli dodatkowo ![]() , to
, to
| (13.8) |
Dla ![]() oszacowanie błędu (13.8) wynika z lematu Céa (twierdzenie 13.2) i z twierdzenia 13.4.
oszacowanie błędu (13.8) wynika z lematu Céa (twierdzenie 13.2) i z twierdzenia 13.4.
Zauważmy, że z definicji przestrzeni ![]() wynika, że jeśli
wynika, że jeśli ![]() to dla dowolnego
to dla dowolnego ![]() istnieje
istnieje ![]() takie, że
takie, że
Następnie z lematu Céa (twierdzenie 13.2), nierówności trójkąta i z oszacowania z twierdzenia 13.4 otrzymujemy:
dla ![]() stałej z lematu Céa i
stałej z lematu Céa i ![]() stałej z twierdzenia 13.4.
Stąd wynika zbieżność
stałej z twierdzenia 13.4.
Stąd wynika zbieżność ![]() do
do ![]() w
w ![]() dla
dla ![]() .
.
Dla dowolnego obszaru wielokątnego (wielościennego) niech ![]() będzie rodziną triangulacji trójkątnych, jak w twierdzeniu 13.4, i niech dla
będzie rodziną triangulacji trójkątnych, jak w twierdzeniu 13.4, i niech dla ![]()
Przestrzeń ![]() nazywamy ciągłą przestrzenią elementu liniowego dla
nazywamy ciągłą przestrzenią elementu liniowego dla ![]() , kwadratowego dla
, kwadratowego dla ![]() i kubicznego dla
i kubicznego dla ![]() .
Wtedy:
.
Wtedy:
13.8. Zadania
Ćwiczenie 13.1
Udowodnij (13.6).
Ćwiczenie 13.2
Niech ![]() dla
dla ![]() .
Pokaż, że
.
Pokaż, że ![]() zdefiniowane dla
zdefiniowane dla ![]() jest ograniczonym funkcjonałem liniowym na
jest ograniczonym funkcjonałem liniowym na ![]() .
.
Ćwiczenie 13.3
Niech ![]() będzie funkcjonałem liniowy na
będzie funkcjonałem liniowy na ![]() . Tu
. Tu ![]() .
Pokaż, że istnieją
.
Pokaż, że istnieją ![]() dla
dla ![]() , takie, że
, takie, że
![]() dla dowolnego
dla dowolnego ![]() .
.
Ćwiczenie 13.4 (trick Nitsche'go)
Rozpatrzmy zadanie dualne do (13.5): znaleźć ![]()
Pokaż, że ma ono jednoznaczne rozwiązanie takie, że
![]()
Dodatkowo zakładamy regularność rozwiązania dualnego
(13.5): tzn., że dla dowolnego ![]() zachodzi:
zachodzi:
![]() z
z ![]() oraz, że
oraz, że ![]() taki, że jeśli
taki, że jeśli ![]() to
to ![]() .
.
Pokaż, że biorąc ![]() dla
dla ![]() rozwiązania (13.3) otrzymamy:
rozwiązania (13.3) otrzymamy:
Ćwiczenie 13.5
Dla liniowej przestrzeni elementu skończonego ![]() na kwadracie jednostkowym z rozdziału 12.1.2 pokaż, że
na kwadracie jednostkowym z rozdziału 12.1.2 pokaż, że
gdzie ![]() rozwiązanie (12.1).
rozwiązanie (12.1).
Wystarczy sprawdzić założenia wniosku 13.4.
Wykorzystaj wynik poprzedniego zadania.




