Zagadnienia

14.1 Schematy różnicowe dla modelowych równań parabolicznych
- 14.1.1 Przypadek jednowymiarowy
- 14.1.2 Przypadek dwuwymiarowy na kwadracie
14.2 Metoda elementu skończonego dla modelowych zadań
- 14.2.1 Przypadek jednowymiarowy
- 14.2.2 Przypadek dwuwymiarowy
14.3 Zadania

14. Metody numeryczne rozwiązywania równań parabolicznych drugiego rzędu

W tym rozdziale zajmiemy się metodami rozwiązywania równań ewolucyjnych drugiego rzędu, czyli równaniami parabolicznymi (2.9).

Takie równania możemy przedstawić abstrakcyjnie jako zadanie znalezienia funkcji $u:[0,T]\rightarrow V$ spełniającej:

	$\displaystyle\frac{du}{dt}-Lu(t)$	$\displaystyle=$	$\displaystyle f(t)\qquad t\in(0,T]$		(14.1)
	$\displaystyle u(0)$	$\displaystyle=$	$\displaystyle u_{0}\in V,$		(14.2)

dla $V$ przestrzeni Hilberta, czy - ogólniej - Banacha, $L$ operatora liniowego określonego dla elementów z $V$ i danej funkcji $f$ określonej na $(0,T]$ o wartościach w $V^{*}$ z przestrzeni sprzężonej. Dane równanie możemy zdyskretyzować po przestrzeni wprowadzając przestrzeń dyskretną skończenie wymiarową $V^{h}$ aproksymującą $V$ , operator $L_{h}$ określony na $V^{h}$ aproksymujący $L$ , funkcję $u_{{0,h}}$ aproksymująca $u_{0}$ , oraz $f_{h}:(0,T)\rightarrow V_{h}$ przybliżenie $f$ . $V^{h}$ może być zbudowane metodą różnic skończonych albo elementu skończonego, lub jeszcze inną metodą dyskretyzacji np. metodą spektralną nie omawianą w tym skrypcie, por. np. [26].

Za aproksymację problemu wyjściowego możemy przyjąć $u_{h}:[0,T]\rightarrow V^{h}$ rozwiązanie następującego układu równań zwyczajnych pierwszego rzędu z warunkami początkowymi:

	$\displaystyle\frac{du_{h}}{dt}-L_{h}u_{h}(t)$	$\displaystyle=$	$\displaystyle f_{h}(t)\qquad t\in(0,T]$		(14.3)
	$\displaystyle u_{h}(0)$	$\displaystyle=$	$\displaystyle u_{{0,h}}\in V^{h}.$

Następnie ten układ możemy rozwiązać przy pomocy jednego ze schematów dla równań zwyczajnych opisanych w pierwszych rozdziałach niniejszego skryptu (por. rozdziały 3-6).

Jeśli chodzi o analizę takich schematów, to stosuje się dwa podejścia: pierwszym jest szacowanie w odpowiedniej normie $u(t)-u_{h}(t)$ (jeśli $V_{h}\not\subset V$ to z odpowiednim przedłużeniem $r_{h}u_{h}\in V$ ), a następnie skorzystanie z ogólnej teorii zbieżności dla schematów dla równań zwyczajnych zastosowanych do rozwiązania (14.3). Drugim podejściem jest konstrukcja schematu całkowicie dyskretnego. Np. dyskretyzujemy (14.3) po czasie jakimś schematem dla zadań początkowych dla równań zwyczajnych, np. którymś ze schematów Eulera, czy trapezów lub jakimś schematem wyższego rzędu, a następnie przeprowadzamy analizę tak powstałego schematu dyskretnego.

Jeśli dyskretyzujemy równanie po zmiennej przestrzennej metodą różnic skończonych, a następnie po czasie - za pomocą jakiegoś schematu ze stałym krokiem całkowania, to tak otrzymany schemat możemy analizować korzystając z ogólnej teorii schematów różnicowych Laxa (por. rozdział 8.1).

Jeśli dyskretyzujemy wyjściowe zadanie paraboliczne przy pomocy metody elementu skończonego, to częściej - choć nie zawsze - do analizy stosuje się podejście pierwsze; tzn.: najpierw badamy błąd w odpowiedniej normie przestrzeni Sobolewa pomiędzy $u$ a $u_{h}$ rozwiązaniem (14.3), a następnie układ (14.3) przepisujemy jako układ równań zwyczajnych na współczynniki rozwiązania w ustalonej bazie $V^{h}$ .

14.1. Schematy różnicowe dla modelowych równań parabolicznych

W tym rozdziale przedstawimy kilka możliwych schematów dla modelowych równań parabolicznych w jednym i dwóch wymiarach.

14.1.1. Przypadek jednowymiarowy

Rozpatrzmy następujące równanie paraboliczne z jednorodnymi warunkami brzegowymi: należy znaleźć funkcję $u$ określoną na $[0,T]$ taką, że

$\displaystyle u_{t}-u_{{xx}}+cu$	$\displaystyle=$	$\displaystyle f(t,x)\qquad t\in(0,T]\quad x\in\Omega=(0,l)$	(14.4)
$\displaystyle u(t,0)=u(t,l)$	$\displaystyle=$	$\displaystyle 0\qquad t\in[0,T]$
$\displaystyle u(0,x)$	$\displaystyle=$	$\displaystyle u_{0}(x)\qquad x\in(0,l)$

dla $f$ danej funkcji ciągłej określonej na $[0,T]\times(0,l)$ i ciągłej funkcji $u_{0}$ określonej na $(0,l)$ i $c$ stałej nieujemnej.

Wprowadzając siatkę jednorodną w obszarze $\Omega$ : $\overline{\Omega}_{h}=\{ x_{k}\} _{{k=0}}^{M}$ z $x_{k}=k*h$ dla $h=l/M$ ( $\Omega _{h}=\{ x_{k}\} _{{k=1}}^{{M-1}}$ ) i zastępując operator

$-\frac{\partial^{2}}{\partial x^{2}}+c$ przez operator siatkowy dyskretny $-\overline{\partial}\partial _{h}+c$ , por. (7.3), dobrze określony dla funkcji dyskretnych na siatce, otrzymujemy układ równań zwyczajnych, którego rozwiązanie powinno aproksymować (14.4):

$\displaystyle\frac{du_{h}}{dt}(t,x)-\overline{\partial}\partial _{h}u_{h}(t,x)+cu_{h}(t,x)$	$\displaystyle=$	$\displaystyle f(t,x)\qquad t\in(0,T],\quad x\in\Omega _{h},$
$\displaystyle u_{h}(t,x_{0})=u_{h}(t,x_{M})$	$\displaystyle=$	$\displaystyle 0\qquad t\in[0,T],$	(14.5)
$\displaystyle u_{h}(0,x)$	$\displaystyle=$	$\displaystyle u_{0}(x)\qquad x\in\Omega _{h}.$

Jeśli wprowadzimy dyskretne kroki czasowe na odcinku $[0,T]$ : $t_{n}=n*\tau$ dla $n=0,\ldots,N$ i $\tau=T/N$ , to układ równań zwyczajnych (14.1.1) możemy zdyskredytować po czasie używając któregoś ze schematów ze stałym krokiem dla równań zwyczajnych. Czyli np.: otwarty schemat Eulera daje nam schemat różnicowy (zwany otwartym schematem Eulera dla równania parabolicznego) polegający na tym, że należy znaleźć $\{ u^{n}_{k}\} _{{k=1,\ldots,M;n=0,\ldots,N}}$ takie, że

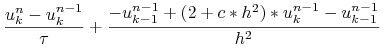$\displaystyle\frac{u^{n}_{k}-u^{{n-1}}_{k}}{\tau}+\frac{-u^{{n-1}}_{{k-1}}+(2+ch^{2})u^{{n-1}}_{k}-u^{{n-1}}_{{k-1}}}{h^{2}}$	$\displaystyle=$	$\displaystyle f^{{n-1}}_{k}\qquad 0<k<M,\; n=1,\ldots,N$
$\displaystyle u^{n}_{0}=u^{n}_{M}$	$\displaystyle=$	$\displaystyle 0\qquad n=0,\ldots,N$	(14.6)
$\displaystyle u^{0}_{k}$	$\displaystyle=$	$\displaystyle u_{0}(x_{k})\qquad k=1,\ldots,M-1$

dla $f^{n}_{k}=f(t_{n},x_{k})$ . Tutaj przyjęliśmy oznaczenie, że szukane przybliżenie $u_{h}(t_{n},x_{k})$ oznaczamy przez $u^{n}_{k}$ .

Powyższy schemat możemy potraktować jako schemat różnicowy na siatce dyskretnej $\Omega _{{\tau,h}}=\{(t_{n},x_{k})\} _{{n,k}}$ z parametrem siatki $\max(\tau,h)$ dla obszaru wyjściowego $\Omega _{T}=(0,T]\times\Omega$ i operatorem różnicowym (siatkowym) $L_{{\tau,h}}=\partial _{\tau}-\overline{\partial}\partial _{h}+cI$ , por. (7.2), przybliżającym na $\Omega _{{\tau,h}}$ operator paraboliczny $L=\frac{\partial}{\partial t}-\frac{\partial^{2}}{\partial x^{2}}+cI$ . Następnie można pokazać, że jeśli $u$ rozwiązanie wyjściowego problemu jest dostatecznie gładkie, to otrzymujemy: $|L_{{\tau,h}}u(t_{n},x_{k})-Lu(t_{n},x_{k})|=O(\tau+h^{2})=O(\max(\tau,h^{2}))$ , czyli rząd aproksymacji schematu wynosi jeden (por. definicję 8.4). A bardziej szczegółowo - rząd aproksymacji schematu wynosi jeden względem $\tau$ , a względem $h$ wynosi dwa.

Można pokazać stabilność operatora różnicowego $L_{{\tau,h}}$ w odpowiednich normach dyskretnych (por. definicję 8.5), tzn. odpowiednia norma dyskretna $u_{h}$ jest nie większa niż stała niezależna od $h,\tau$ pomnożona przez odpowiednie normy dyskretne $\{ f^{n}_{k}\} _{{n,k}}$ i $\{ u^{0}_{k}\} _{k}$ .

Przypomnijmy, że jeśli schemat różnicowy jest stabilny i posiada odpowiedni rząd aproksymacji schematu, to jest zbieżny z odpowiednim rzędem, por. rozdział 8.1.

Niestety - stabilność jest tylko warunkowa, tzn. tylko dla $h$ i $\tau$ spełniających odpowiedni warunek. Mówimy wtedy, że schemat jest stabilny warunkowo. Z praktycznego punktu widzenia lepiej byłoby gdyby schemat był stabilny absolutnie, tzn. dla dowolnej pary $\tau>0,h>0$ .

Analogicznie możemy wprowadzić zamknięty schemat Eulera dla modelowego zadania parabolicznego stosując zamknięty schemat Eulera dla równań zwyczajnych do dyskretyzacji po czasie (14.1.1):

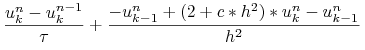$\displaystyle\frac{u^{n}_{k}-u^{{n-1}}_{k}}{\tau}+\frac{-u^{n}_{{k-1}}+(2+ch^{2})u^{n}_{k}-u^{n}_{{k-1}}}{h^{2}}$	$\displaystyle=$	$\displaystyle f^{n}_{k}\qquad 0<k<M,\quad n=1,2,\ldots,N$
$\displaystyle u^{n}_{0}=u^{n}_{M}$	$\displaystyle=$	$\displaystyle 0\qquad n=0,\ldots,N$	(14.7)
$\displaystyle u^{0}_{k}$	$\displaystyle=$	$\displaystyle u_{0}(x_{k})\qquad k=1,\ldots,M-1$

Rząd lokalnego błędu aproksymacji zamkniętego schematu Eulera jest taki sam jak otwartego schematu Eulera, ale dla $c>0$ schemat ten jest absolutnie stabilny w dyskretnej normie maksimum. Kolejny schemat Cranka-Nicholson otrzymany po zastosowaniu schematu trapezów, por. (4.7), do (14.1.1):

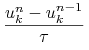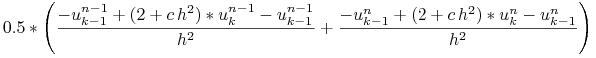$\displaystyle\frac{u^{n}_{k}-u^{{n-1}}_{k}}{\tau}$	$\displaystyle+$	$\displaystyle 0.5\left(\frac{-u^{{n-1}}_{{k-1}}+(2+c\, h^{2})u^{{n-1}}_{k}-u^{{n-1}}_{{k-1}}}{h^{2}}+\frac{-u^{n}_{{k-1}}+(2+c\, h^{2})*u^{n}_{k}-u^{n}_{{k-1}}}{h^{2}}\right)$
		$\displaystyle=0.5*(f^{{n-1}}_{k}+f^{n}_{k})\qquad 0<k<M,\quad n=1,2,\ldots,N$
		$\displaystyle u^{n}_{0}=u^{n}_{M}=0\qquad n=0,\ldots,N$
		$\displaystyle u^{0}_{k}=u_{0}(x_{k})\qquad k=1,\ldots,M-1$

Można pokazać, że lokalny błąd aproksymacji tego schematu jest jak $O(\tau^{2}+h^{2})$ .

W przypadku zamkniętego schematu Eulera i schematu Cranka-Nicholson można pokazać ich bezwarunkową stabilność dla $c\geq 0$ w specjalnie dobranych normach dyskretnych.

14.1.2. Przypadek dwuwymiarowy na kwadracie

W tym rozdziale zajmiemy się ze względu na prostotę prezentacji modelowym równaniem parabolicznym z jednorodnymi warunkami brzegowymi na kwadracie $\Omega=(0,1)^{2}$ . Chcemy znaleźć funkcję $u$ określoną na $[0,T]$ taką, że

$\displaystyle u_{t}-\triangle u+cu$	$\displaystyle=$	$\displaystyle f(t,x)\qquad t\in(0,T]\quad x\in\Omega=(0,1)^{2}$	(14.8)
$\displaystyle u(t,s)$	$\displaystyle=$	$\displaystyle 0\qquad t\in[0,T]\quad s\in\partial\Omega$
$\displaystyle u(0,x)$	$\displaystyle=$	$\displaystyle u_{0}(x)\qquad x\in\Omega$

gdzie $f$ - to dana funkcja ciągła określona na $(0,T]\times(0,1)^{2}$ , $u_{0}$ - to funkcja ciągła określona na $[0,1]^{2}$ , a $c$ - to stała nieujemna.

Wprowadzając siatkę jednorodną w obszarze $\Omega$ jak w rozdziale 7.2: $\Omega _{h},\overline{\Omega}_{h},\partial\Omega _{h}$ dla $h=1/M$ , i zastępując operator $-\triangle+c$ przez operator siatkowy dyskretny $-\sum _{{s=1}}^{2}\overline{\partial}\partial _{{s,h}}+c$ por. (7.9) dobrze określony dla funkcji dyskretnych na jednorodnej siatce, otrzymujemy układ równań zwyczajnych, którego rozwiązanie powinno aproksymować (14.8):

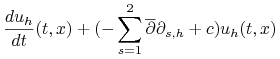$\displaystyle\frac{du_{h}}{dt}(t,x)+(-\sum _{{s=1}}^{2}\overline{\partial}\partial _{{s,h}}+c)u_{h}(t,x)$	$\displaystyle=$	$\displaystyle f(t,x)\qquad x\in\Omega _{h},\quad t\in(0,T]$
$\displaystyle u_{h}(t,x_{0})$	$\displaystyle=$	$\displaystyle 0\qquad t\in[0,T]\quad s\in\partial\Omega _{h}$	(14.9)
$\displaystyle u_{h}(0,x)$	$\displaystyle=$	$\displaystyle u_{0}(x)\qquad x\in\Omega _{h}$

Tak jak w przypadku jednowymiarowym (por. rozdział 14.1.1), wprowadzamy dyskretną siatkę po zmiennej czasowej z krokiem $\tau$ na odcinku $[0,T]$ : $t_{n}=n*\tau$ dla $n=0,\ldots,N$ i $\tau=T/N$ i otrzymujemy dyskretyzację układu równań zwyczajnych (14.1.2) używając któregoś ze schematów ze stałym krokiem dla równań zwyczajnych.

Otwarty schemat Eulera daje nam następujący schemat polegający na znalezieniu $\{ u^{n}_{{k,l}}\}$ takiego, że:

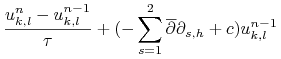$\displaystyle\frac{u^{n}_{{k,l}}-u^{{n-1}}_{{k,l}}}{\tau}+(-\sum _{{s=1}}^{2}\overline{\partial}\partial _{{s,h}}+c)u^{{n-1}}_{{k,l}}$	$\displaystyle=$	$\displaystyle f^{{n-1}}_{{k,l}}\qquad 0<k,l<M,\; n=1,\ldots,N$
$\displaystyle u^{n}_{{k,l}}$	$\displaystyle=$	$\displaystyle 0\qquad n=0,\ldots,N\quad k,l=0,M$	(14.10)
$\displaystyle u^{0}_{{k,l}}$	$\displaystyle=$	$\displaystyle u_{0}(kh,lh)\qquad k,l=1,\ldots,M-1$

Przybliżenie $u_{h}(t_{n},(k*h,l*h))$ oznaczamy przez $u^{n}_{{k,l}}$ .

W szczególności otrzymujemy

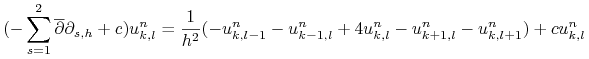$(-\sum _{{s=1}}^{2}\overline{\partial}\partial _{{s,h}}+c)u^{n}_{{k,l}}=\frac{1}{h^{2}}(-u^{n}_{{k,l-1}}-u^{n}_{{k-1,l}}+4u^{n}_{{k,l}}-u^{n}_{{k+1,l}}-u^{n}_{{k,l+1}})+cu^{n}_{{k,l}}$

Analogicznie możemy zdefiniować schemat zamknięty Eulera lub schemat Cranka-Nicholson, czyli schemat trapezów zastosowany do (14.1.2).

14.2. Metoda elementu skończonego dla modelowych zadań

14.2.1. Przypadek jednowymiarowy

Rozpatrzmy ponownie jednowymiarowe modelowe zadanie (14.4). Jego słabe sformułowanie wprowadzamy analogicznie jak w rozdziale 11. Mnożąc równanie paraboliczne (14.4) przez funkcję testową z $C^{\infty}_{0}(0,l)$ , całkując po $(0,l)$ i stosując wzór na całkowanie przez części otrzymujemy równanie:

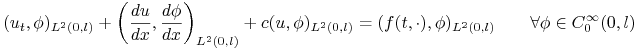$(u_{t},\phi)_{{L^{2}(0,l)}}+\left(\frac{du}{dx},\frac{d\phi}{dx}\right)_{{L^{2}(0,l)}}+c(u,\phi)_{{L^{2}(0,l)}}=(f(t,\cdot),\phi)_{{L^{2}(0,l)}}\qquad\forall\phi\in C^{\infty}_{0}(0,l)$

z warunkiem początkowym

$(u(0),\phi)_{{L^{2}(0,l)}}=(u_{0},\phi)_{{L^{2}(0,l)}}\qquad\forall\phi\in C^{\infty}_{0}(0,l).$

Korzystając z tego, że $H^{1}_{0}(0,l)$ jest domknięciem $C^{\infty}_{0}(0,l)$ w normie $H^{1}$ można pokazać, że powyższe równanie jest równoważne znalezieniu funkcji $u:[0,T]\rightarrow H^{1}_{0}(\Omega)$ takiej, że

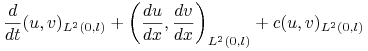	$\displaystyle\frac{d}{dt}(u,v)_{{L^{2}(0,l)}}+\left(\frac{du}{dx},\frac{dv}{dx}\right)_{{L^{2}(0,l)}}+c(u,v)_{{L^{2}(0,l)}}$	$\displaystyle=$	$\displaystyle(f(t,\cdot),v)_{{L^{2}(0,l)}}\quad\forall v\in H^{1}_{0}(0,l),$		(14.11)
	$\displaystyle(u(0),v)_{{L^{2}(0,l)}}$	$\displaystyle=$	$\displaystyle(u_{0},v)_{{L^{2}(0,l)}}\qquad\forall v\in H^{1}_{0}(0,l)$

dla $0<t\leq T$ , co jest słabym (wariacyjnym) sformułowaniem (14.4), które stanowi wyjście do konstrukcji dyskretyzacji równania parabolicznego za pomocą metody elementu skończonego. Niech $T_{h}([0,l])=\{[x_{k},x_{{k+1}}\}$ będzie triangulacją równomierną $[0,l]$ zdefiniowaną jak w rozdziale 11.1.2, tzn. $x_{k}=k*h$ dla $h=l/N$ i niech $V^{h}$ będzie przestrzenią funkcji ciągłych kawałkami liniowych (tzn. liniowych na elementach $[x_{k},x_{{k+1}}]$ ) zerujących się w końcach odcinka $[0,l]$ . Oczywiście zachodzi $V^{h}\subset H^{1}_{0}(0,l)$ .

Wtedy możemy zdefiniować dyskretyzację po przestrzeni zadania (14.11).

Znajdź funkcję $u_{h}:[0,T]\rightarrow V^{h}$ taką, że dla $0<t\leq T$ i dowolnego $v_{h}\in V^{h}$ zachodzi:

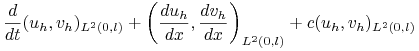	$\displaystyle\frac{d}{dt}(u_{h},v_{h})_{{L^{2}(0,l)}}+\left(\frac{du_{h}}{dx},\frac{dv_{h}}{dx}\right)_{{L^{2}(0,l)}}+c(u_{h},v_{h})_{{L^{2}(0,l)}}$	$\displaystyle=$	$\displaystyle(f(t,\cdot),v_{h})_{{L^{2}(0,l)}}$		(14.12)
	$\displaystyle(u_{h}(0),v_{h})_{{L^{2}(0,l)}}$	$\displaystyle=$	$\displaystyle(u_{0},v_{h})_{{L^{2}(0,l)}}$

Biorąc bazę nodalną tej przestrzeni $(\phi _{k})_{{k=1}}^{{N-1}}$ (por. (11.3)) i rysunek 11.1 na str. 11.1, otrzymujemy $u_{h}=\sum _{{k=1}}^{{N-1}}u_{k}\phi _{k}$ i

	$\displaystyle M_{h}\frac{d}{dt}\vec{u}+(A_{h}+cM_{h})\vec{u}=\vec{f}(t)$
	$\displaystyle M_{h}\vec{u}(0)=\vec{u}_{{0,h}}$

dla $\vec{u}=(u_{k})_{k}$ , $M_{h}=((\phi _{k},\phi _{l})_{{L^{2}(0,l)}})_{{k,l}}$ , $A_{h}=((\frac{d\phi _{k}}{dx},\frac{d\phi _{l}}{dx})_{{L^{2}(0,l)}})_{{k,l}}$ , $\vec{u}_{{0,h}}=((u_{0},\phi _{k})_{{L^{2}(0,l)}})_{k}$ i wektora prawej strony $\vec{f}=(f_{1},\ldots,f_{{N-1}})^{T}$ dla $f_{k}(t)=(f(t),\phi _{k})_{{L^{2}(0,l)}}$ . Z tego otrzymujemy

	$\displaystyle\frac{d}{dt}\vec{u}+(M_{h}^{{-1}}A_{h}+cI)\vec{u}=M_{h}^{{-1}}\vec{f}(t)=:\vec{g}(t)$
	$\displaystyle\vec{u}(0)=M_{h}^{{-1}}\vec{u}_{{0,h}}:=\vec{u}_{0}.$

Proszę zauważyć, że jest to układ równań zwyczajnych liniowych z warunkiem początkowym, więc ma jednoznaczne rozwiązanie na $[0,T]$ , co wynika z ogólnej teorii równań różniczkowych zwyczajnych, por. np. rozdział 3.2 lub [23]. Do powyższego układu równań możemy zastosować dowolny schemat rozwiązywania równań zadania początkowego dla równań zwyczajnych.

Macierze $M_{h}$ i $A_{h}$ są symetryczne i dodatnio określone.

Można pokazać, że macierz $M_{h}^{{-1}}A_{h}$ ma wartości własne ujemne o module od jeden do rzędu $h^{{-2}}$ , czyli bardzo dużym module dla małych $h$ . Zatem dla $c=0$ układ równań zwyczajnych jest sztywny zgodnie z definicją z rozdziału 6. Należy tu stosować schematy całkowania równań zwyczajnych stosowne do zadań sztywnych.

14.2.2. Przypadek dwuwymiarowy

Rozpatrzmy dwuwymiarowe modelowe zadanie na dowolnym obszarze wielokątnym na płaszczyźnie $\Omega$ , czyli zastępując kwadrat przez $\Omega$ w (14.8). Jego słabe sformułowanie otrzymujemy analogicznie jak w rozdziale 11, lub w przypadku jednowymiarowym (por. rozdział 14.2.1). Mnożąc równanie paraboliczne z (14.8) przez funkcję testową z $C^{\infty}_{0}(\Omega)$ , całkując po $\Omega$ i stosując wzory Greene'a otrzymujemy:

$(u_{t},\phi)_{{L^{2}(\Omega)}}+a(u,v)=(f(t,\cdot),\phi)_{{L^{2}(\Omega)}}\qquad\forall\phi\in C^{\infty}_{0}(\Omega)$

dla $0<t\leq T$ , $a(u,v)=(\nabla u,\nabla\phi)_{{L^{2}(\Omega)}}+c(u,\phi)_{{L^{2}(\Omega)}}$ oraz $u$ spełnia warunek początkowy $(u(0),\phi)_{{L^{2}(\Omega)}}=(u_{0},\phi)_{{L^{2}(\Omega)}}$ .

Jak w rozdziale 14.2.1 otrzymujemy, że powyższe równanie jest równoważne znalezieniu funkcji $u:[0,T]\rightarrow H^{1}_{0}(\Omega)$ takiej, że

	$\displaystyle\frac{d}{dt}(u,v)_{{L^{2}(\Omega)}}+a(u,v)$	$\displaystyle=$	$\displaystyle(f(t,\cdot),v)_{{L^{2}(\Omega)}}\quad\forall v\in H^{1}_{0}(\Omega),$		(14.13)
	$\displaystyle(u(0),v)_{{L^{2}(\Omega)}}$	$\displaystyle=$	$\displaystyle(u_{0},v)_{{L^{2}(\Omega)}}\quad\forall v\in H^{1}_{0}(\Omega)$

dla $0<t\leq T$ , co jest słabym, wariacyjnym sformułowaniem (14.8), które stanowi wyjście do konstrukcji dyskretyzacji równania parabolicznego za pomocą metody elementu skończonego. Rozpatrzmy $T_{h}(\Omega)$ triangulacje równomierną $\Omega$ , złożoną z przystających trójkątów, zdefiniowaną jak w rozdziale 12 i $V^{h}$ - przestrzeń funkcji ciągłych kawałkami liniowych na tej triangulacji, zerujących się na brzegu, czyli przestrzenią liniowego elementu skończonego (por. rozdział 12).

Dyskretyzację po przestrzeni zadania (14.13) definiujemy: znajdź funkcję $u_{h}:[0,T]\rightarrow V^{h}$ taką, że dla $0<t\leq T$ i dowolnego $v_{h}\in V^{h}$ :

	$\displaystyle\frac{d}{dt}(u_{h},v_{h})_{{L^{2}(\Omega)}}+a(u_{h},v_{h})$	$\displaystyle=$	$\displaystyle(f(t,\cdot),v_{h})_{{L^{2}(\Omega)}}$		(14.14)
	$\displaystyle(u_{h}(0),v_{h})_{{L^{2}(\Omega)}}$	$\displaystyle=$	$\displaystyle(u_{0},v_{h})_{{L^{2}(\Omega)}}.$

Otrzymaliśmy zatem ponownie układ równań zwyczajnych liniowych z warunkiem początkowym, który po wprowadzeniu standardowej bazy daszkowej $\{\phi _{{kl}}\}$ dla $V^{h}$ , por. (12.1.2), możemy przepisać jako zadanie początkowe na funkcje-współczynniki $\alpha _{{k,l}}(t)$ takie, że $u_{h}(t)=\sum _{{k,l}}\alpha _{{k,l}}(t)\phi _{{kl}}$ . Następnie to zadanie początkowe możemy rozwiązać za pomocą jakiegoś schematu, np. otwartego lub zamkniętego schematu Eulera, lub schematu trapezów. Okazuje się, że - tak samo jak w przypadku jednowymiarowym - dla $c=0$ powstające układy równań zwyczajnych są sztywne. Dlatego w praktyce stosuje się odpowiednie schematy dla zadań sztywnych.

14.3. Zadania

Ćwiczenie 14.1

Zbadaj rzędy błędów aproksymacji otwartego schematu Eulera (14.1.1) i zamkniętego schematu Eulera (14.1.1) dla dyskretyzacji modelowego problemu jednowymiarowego w dyskretnej normie maksimum przyjmując, że rozwiązanie jest dostatecznie gładkie. Ustal, jaka minimalna gładkość rozwiązania jest konieczna, tzn. znajdź najmniejsze $r$ takie, że jeśli rozwiązanie $u\in C^{r}$ , to rząd aproksymacji schematu jest możliwie duży.

Ćwiczenie 14.2

Zbadaj stabilność zamkniętego schematu Eulera (14.1.1) dla dyskretyzacji modelowego problemu jednowymiarowego w dyskretnej normie maksimum dla $c>0$ . Wywnioskuj zbieżność dyskretną schematu w tejże normie.

Wskazówka:

Zastosuj twierdzenie 9.1, a do wykazania zbieżności zastosuj ogólną teorię zbieżności schematów różnicowych Laxa z rozdziału 8.

Ćwiczenie 14.3

Zbadaj rząd błędu aproksymacji schematu Cranka-Nicholson dla $c>0$ dla dyskretyzacji modelowego problemu jednowymiarowego w dyskretnej normie maksimum przyjmując, że rozwiązanie jest dostatecznie gładkie. Ustal, jaka minimalna gładkość rozwiązania jest konieczna, aby schemat miał ten rząd. Zbadaj stabilność tego schematu w dyskretnej normie maksimum: czy jest warunkowa, czy bezwarunkowa? Zbadaj zbieżność w dyskretnej normie maksimum.

Ćwiczenie 14.4

$\Omega=(0,1)^{2}$

Zapisz (14.14) w postaci liniowego zadania początkowego:

$M_{h}\frac{d\vec{u}}{dt}(t)+A_{h}\vec{u}(t)=\vec{f}(t),\qquad\vec{u}(0)=\vec{u}_{0}$

dla $\vec{u}(t)=\{ c_{{k,l}}(t)\} _{{k,l}}$ współczynników $u_{h}(t)$ w bazie daszkowej $V^{h}$ (por. (12.1.2)) i $M_{h},A_{h}$ macierzy stałych.
Wypisz wzory na otwarty i zamknięty schemat Eulera zastosowany do tego zadania początkowego.