Zagadnienia
14. Metody numeryczne rozwiązywania równań parabolicznych drugiego rzędu
W tym rozdziale zajmiemy się metodami rozwiązywania równań ewolucyjnych drugiego rzędu, czyli równaniami parabolicznymi (2.9).
Takie równania możemy przedstawić abstrakcyjnie jako
zadanie znalezienia
funkcji ![]() spełniającej:
spełniającej:
| (14.1) | |||||
| (14.2) |
dla ![]() przestrzeni Hilberta, czy - ogólniej - Banacha,
przestrzeni Hilberta, czy - ogólniej - Banacha,
![]() operatora liniowego określonego dla elementów z
operatora liniowego określonego dla elementów z ![]() i danej funkcji
i danej funkcji ![]() określonej na
określonej na ![]() o wartościach w
o wartościach w ![]() z przestrzeni sprzężonej.
Dane równanie możemy zdyskretyzować po przestrzeni wprowadzając przestrzeń dyskretną skończenie wymiarową
z przestrzeni sprzężonej.
Dane równanie możemy zdyskretyzować po przestrzeni wprowadzając przestrzeń dyskretną skończenie wymiarową ![]() aproksymującą
aproksymującą ![]() , operator
, operator ![]() określony na
określony na ![]() aproksymujący
aproksymujący ![]() , funkcję
, funkcję ![]() aproksymująca
aproksymująca ![]() , oraz
, oraz ![]() przybliżenie
przybliżenie ![]() .
.
![]() może być zbudowane metodą różnic skończonych albo elementu skończonego, lub jeszcze inną metodą dyskretyzacji np. metodą spektralną nie omawianą w tym skrypcie, por. np. [26].
może być zbudowane metodą różnic skończonych albo elementu skończonego, lub jeszcze inną metodą dyskretyzacji np. metodą spektralną nie omawianą w tym skrypcie, por. np. [26].
Za aproksymację problemu wyjściowego możemy przyjąć ![]() rozwiązanie następującego układu równań zwyczajnych pierwszego rzędu z warunkami początkowymi:
rozwiązanie następującego układu równań zwyczajnych pierwszego rzędu z warunkami początkowymi:
| (14.3) | |||||
Następnie ten układ możemy rozwiązać przy pomocy jednego ze schematów dla równań zwyczajnych opisanych w pierwszych rozdziałach niniejszego skryptu (por. rozdziały 3-6).
Jeśli chodzi o analizę takich schematów, to stosuje się
dwa podejścia:
pierwszym jest
szacowanie w odpowiedniej normie ![]() (jeśli
(jeśli ![]() to z odpowiednim przedłużeniem
to z odpowiednim przedłużeniem ![]() ),
a następnie skorzystanie z ogólnej teorii zbieżności dla schematów dla równań zwyczajnych
zastosowanych do rozwiązania (14.3). Drugim podejściem jest
konstrukcja schematu całkowicie dyskretnego.
Np. dyskretyzujemy (14.3) po czasie jakimś schematem dla zadań początkowych dla równań zwyczajnych, np. którymś ze schematów Eulera, czy trapezów lub jakimś schematem wyższego rzędu, a następnie przeprowadzamy analizę tak powstałego schematu dyskretnego.
),
a następnie skorzystanie z ogólnej teorii zbieżności dla schematów dla równań zwyczajnych
zastosowanych do rozwiązania (14.3). Drugim podejściem jest
konstrukcja schematu całkowicie dyskretnego.
Np. dyskretyzujemy (14.3) po czasie jakimś schematem dla zadań początkowych dla równań zwyczajnych, np. którymś ze schematów Eulera, czy trapezów lub jakimś schematem wyższego rzędu, a następnie przeprowadzamy analizę tak powstałego schematu dyskretnego.
Jeśli dyskretyzujemy równanie po zmiennej przestrzennej metodą różnic skończonych, a następnie po czasie - za pomocą jakiegoś schematu ze stałym krokiem całkowania, to tak otrzymany schemat możemy analizować korzystając z ogólnej teorii schematów różnicowych Laxa (por. rozdział 8.1).
Jeśli dyskretyzujemy wyjściowe zadanie paraboliczne przy pomocy metody elementu skończonego, to częściej - choć nie zawsze - do analizy stosuje się podejście pierwsze; tzn.: najpierw badamy błąd w odpowiedniej normie przestrzeni Sobolewa
pomiędzy ![]() a
a ![]() rozwiązaniem (14.3), a następnie
układ (14.3) przepisujemy jako układ równań zwyczajnych na współczynniki rozwiązania w ustalonej bazie
rozwiązaniem (14.3), a następnie
układ (14.3) przepisujemy jako układ równań zwyczajnych na współczynniki rozwiązania w ustalonej bazie ![]() .
.
14.1. Schematy różnicowe dla modelowych równań parabolicznych
W tym rozdziale przedstawimy kilka możliwych schematów dla modelowych równań parabolicznych w jednym i dwóch wymiarach.
14.1.1. Przypadek jednowymiarowy
Rozpatrzmy następujące równanie paraboliczne z jednorodnymi warunkami brzegowymi:
należy znaleźć funkcję ![]() określoną na
określoną na ![]() taką, że
taką, że
| (14.4) | |||||
dla ![]() danej funkcji ciągłej określonej na
danej funkcji ciągłej określonej na ![]() i ciągłej funkcji
i ciągłej funkcji ![]() określonej na
określonej na ![]() i
i ![]() stałej nieujemnej.
stałej nieujemnej.
Wprowadzając siatkę jednorodną w obszarze ![]() :
:
![]() z
z ![]() dla
dla ![]() (
(![]() ) i zastępując operator
) i zastępując operator
![]() przez operator siatkowy dyskretny
przez operator siatkowy dyskretny ![]() ,
por. (7.3),
dobrze określony dla funkcji dyskretnych na siatce, otrzymujemy
układ równań zwyczajnych, którego rozwiązanie powinno aproksymować (14.4):
,
por. (7.3),
dobrze określony dla funkcji dyskretnych na siatce, otrzymujemy
układ równań zwyczajnych, którego rozwiązanie powinno aproksymować (14.4):
| (14.5) | |||||
Jeśli wprowadzimy dyskretne kroki czasowe na odcinku ![]() :
: ![]() dla
dla ![]() i
i ![]() , to
układ równań zwyczajnych (14.1.1) możemy zdyskredytować po czasie
używając któregoś ze schematów ze stałym krokiem dla równań zwyczajnych.
Czyli np.: otwarty schemat Eulera daje nam schemat różnicowy (zwany otwartym schematem Eulera dla równania parabolicznego) polegający na tym, że należy znaleźć
, to
układ równań zwyczajnych (14.1.1) możemy zdyskredytować po czasie
używając któregoś ze schematów ze stałym krokiem dla równań zwyczajnych.
Czyli np.: otwarty schemat Eulera daje nam schemat różnicowy (zwany otwartym schematem Eulera dla równania parabolicznego) polegający na tym, że należy znaleźć ![]() takie, że
takie, że
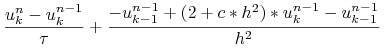 |
|||||
| (14.6) | |||||
dla ![]() .
Tutaj przyjęliśmy oznaczenie, że szukane przybliżenie
.
Tutaj przyjęliśmy oznaczenie, że szukane przybliżenie ![]() oznaczamy przez
oznaczamy przez ![]() .
.
Powyższy schemat możemy potraktować jako schemat różnicowy na siatce dyskretnej
![]() z parametrem siatki
z parametrem siatki ![]() dla obszaru wyjściowego
dla obszaru wyjściowego ![]() i operatorem różnicowym (siatkowym)
i operatorem różnicowym (siatkowym)
![]() ,
por. (7.2), przybliżającym na
,
por. (7.2), przybliżającym na ![]() operator paraboliczny
operator paraboliczny ![]() .
Następnie można pokazać, że jeśli
.
Następnie można pokazać, że jeśli ![]() rozwiązanie wyjściowego problemu jest dostatecznie gładkie,
to otrzymujemy:
rozwiązanie wyjściowego problemu jest dostatecznie gładkie,
to otrzymujemy: ![]() ,
czyli
rząd aproksymacji schematu wynosi jeden
(por. definicję 8.4).
A bardziej szczegółowo - rząd aproksymacji schematu wynosi jeden względem
,
czyli
rząd aproksymacji schematu wynosi jeden
(por. definicję 8.4).
A bardziej szczegółowo - rząd aproksymacji schematu wynosi jeden względem ![]() , a względem
, a względem ![]() wynosi dwa.
wynosi dwa.
Można pokazać stabilność operatora różnicowego ![]() w odpowiednich normach dyskretnych (por. definicję 8.5), tzn. odpowiednia norma dyskretna
w odpowiednich normach dyskretnych (por. definicję 8.5), tzn. odpowiednia norma dyskretna ![]() jest nie większa niż stała niezależna od
jest nie większa niż stała niezależna od ![]() pomnożona przez odpowiednie normy dyskretne
pomnożona przez odpowiednie normy dyskretne
![]() i
i ![]() .
.
Przypomnijmy, że jeśli schemat różnicowy jest stabilny i posiada odpowiedni rząd aproksymacji schematu, to jest zbieżny z odpowiednim rzędem, por. rozdział 8.1.
Niestety - stabilność jest tylko warunkowa, tzn. tylko dla ![]() i
i ![]() spełniających odpowiedni warunek. Mówimy wtedy, że schemat jest stabilny warunkowo.
Z praktycznego punktu widzenia lepiej byłoby gdyby schemat był stabilny absolutnie, tzn. dla dowolnej pary
spełniających odpowiedni warunek. Mówimy wtedy, że schemat jest stabilny warunkowo.
Z praktycznego punktu widzenia lepiej byłoby gdyby schemat był stabilny absolutnie, tzn. dla dowolnej pary ![]() .
.
Analogicznie możemy wprowadzić zamknięty schemat Eulera dla modelowego zadania parabolicznego stosując zamknięty schemat Eulera dla równań zwyczajnych do dyskretyzacji po czasie (14.1.1):
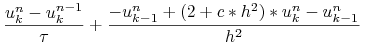 |
|||||
| (14.7) | |||||
Rząd lokalnego błędu aproksymacji zamkniętego schematu Eulera jest taki sam jak otwartego schematu Eulera, ale
dla ![]() schemat ten jest absolutnie stabilny w dyskretnej normie maksimum.
Kolejny schemat Cranka-Nicholson otrzymany po zastosowaniu schematu trapezów,
por. (4.7),
do (14.1.1):
schemat ten jest absolutnie stabilny w dyskretnej normie maksimum.
Kolejny schemat Cranka-Nicholson otrzymany po zastosowaniu schematu trapezów,
por. (4.7),
do (14.1.1):
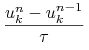 |
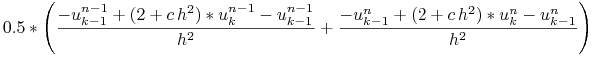 |
|||
Można pokazać, że lokalny błąd aproksymacji tego schematu jest jak ![]() .
.
W przypadku zamkniętego schematu Eulera i schematu Cranka-Nicholson można pokazać ich bezwarunkową stabilność dla ![]() w specjalnie dobranych normach dyskretnych.
w specjalnie dobranych normach dyskretnych.
14.1.2. Przypadek dwuwymiarowy na kwadracie
W tym rozdziale zajmiemy się ze względu na prostotę prezentacji modelowym równaniem parabolicznym z jednorodnymi warunkami brzegowymi na kwadracie ![]() .
Chcemy znaleźć funkcję
.
Chcemy znaleźć funkcję ![]() określoną na
określoną na ![]() taką, że
taką, że
| (14.8) | |||||
gdzie ![]() - to dana funkcja ciągła określona na
- to dana funkcja ciągła określona na ![]() ,
, ![]() - to funkcja ciągła określona na
- to funkcja ciągła określona na ![]() , a
, a ![]() - to stała nieujemna.
- to stała nieujemna.
Wprowadzając siatkę jednorodną w obszarze ![]() jak w rozdziale 7.2:
jak w rozdziale 7.2:
![]() dla
dla ![]() , i zastępując operator
, i zastępując operator
![]() przez operator siatkowy dyskretny
przez operator siatkowy dyskretny ![]() por. (7.9)
dobrze określony dla funkcji dyskretnych na jednorodnej siatce,
otrzymujemy
układ równań zwyczajnych, którego rozwiązanie powinno aproksymować (14.8):
por. (7.9)
dobrze określony dla funkcji dyskretnych na jednorodnej siatce,
otrzymujemy
układ równań zwyczajnych, którego rozwiązanie powinno aproksymować (14.8):
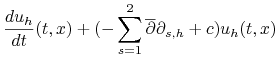 |
|||||
| (14.9) | |||||
Tak jak w przypadku jednowymiarowym (por. rozdział 14.1.1),
wprowadzamy dyskretną siatkę po zmiennej czasowej z krokiem ![]() na odcinku
na odcinku ![]() :
: ![]() dla
dla ![]() i
i ![]() i otrzymujemy dyskretyzację
układu równań zwyczajnych (14.1.2)
używając któregoś ze schematów ze stałym krokiem dla równań zwyczajnych.
i otrzymujemy dyskretyzację
układu równań zwyczajnych (14.1.2)
używając któregoś ze schematów ze stałym krokiem dla równań zwyczajnych.
Otwarty schemat Eulera daje nam następujący schemat polegający na znalezieniu ![]() takiego, że:
takiego, że:
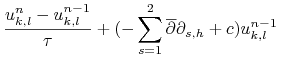 |
|||||
| (14.10) | |||||
Przybliżenie ![]() oznaczamy przez
oznaczamy przez ![]() .
.
W szczególności otrzymujemy
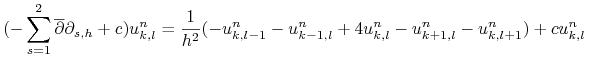 |
Analogicznie możemy zdefiniować schemat zamknięty Eulera lub schemat Cranka-Nicholson, czyli schemat trapezów zastosowany do (14.1.2).
14.2. Metoda elementu skończonego dla modelowych zadań
14.2.1. Przypadek jednowymiarowy
Rozpatrzmy ponownie jednowymiarowe modelowe zadanie (14.4).
Jego słabe sformułowanie wprowadzamy analogicznie jak w rozdziale 11.
Mnożąc równanie paraboliczne (14.4) przez funkcję testową z ![]() , całkując po
, całkując po ![]() i stosując wzór na całkowanie przez części otrzymujemy równanie:
i stosując wzór na całkowanie przez części otrzymujemy równanie:
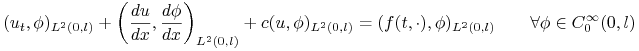 |
z warunkiem początkowym
Korzystając z tego, że ![]() jest domknięciem
jest domknięciem ![]() w normie
w normie ![]() można pokazać,
że powyższe równanie jest równoważne znalezieniu funkcji
można pokazać,
że powyższe równanie jest równoważne znalezieniu funkcji ![]() takiej, że
takiej, że
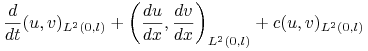 |
(14.11) | ||||
dla ![]() , co jest słabym (wariacyjnym) sformułowaniem (14.4), które stanowi wyjście do konstrukcji dyskretyzacji równania parabolicznego za pomocą metody elementu skończonego.
Niech
, co jest słabym (wariacyjnym) sformułowaniem (14.4), które stanowi wyjście do konstrukcji dyskretyzacji równania parabolicznego za pomocą metody elementu skończonego.
Niech ![]() będzie triangulacją równomierną
będzie triangulacją równomierną ![]() zdefiniowaną jak w rozdziale 11.1.2, tzn.
zdefiniowaną jak w rozdziale 11.1.2, tzn. ![]() dla
dla ![]() i niech
i niech
![]() będzie przestrzenią funkcji ciągłych kawałkami liniowych (tzn. liniowych na elementach
będzie przestrzenią funkcji ciągłych kawałkami liniowych (tzn. liniowych na elementach ![]() ) zerujących się w końcach odcinka
) zerujących się w końcach odcinka ![]() . Oczywiście zachodzi
. Oczywiście zachodzi ![]() .
.
Wtedy możemy zdefiniować dyskretyzację po przestrzeni zadania (14.11).
Znajdź funkcję ![]() taką, że dla
taką, że dla ![]() i dowolnego
i dowolnego ![]() zachodzi:
zachodzi:
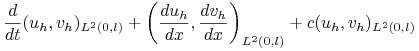 |
(14.12) | ||||
Biorąc bazę nodalną tej przestrzeni ![]() (por. (11.3)) i rysunek 11.1 na str. 11.1,
otrzymujemy
(por. (11.3)) i rysunek 11.1 na str. 11.1,
otrzymujemy ![]() i
i
dla ![]() ,
, ![]() ,
,
![]() ,
,
![]() i wektora prawej strony
i wektora prawej strony
![]() dla
dla ![]() .
Z tego otrzymujemy
.
Z tego otrzymujemy
Proszę zauważyć, że jest to układ równań zwyczajnych liniowych z warunkiem początkowym,
więc ma jednoznaczne rozwiązanie na ![]() , co wynika z ogólnej teorii równań różniczkowych zwyczajnych,
por. np. rozdział 3.2 lub [23].
Do powyższego układu równań możemy zastosować dowolny schemat
rozwiązywania równań zadania początkowego dla równań zwyczajnych.
, co wynika z ogólnej teorii równań różniczkowych zwyczajnych,
por. np. rozdział 3.2 lub [23].
Do powyższego układu równań możemy zastosować dowolny schemat
rozwiązywania równań zadania początkowego dla równań zwyczajnych.
Macierze ![]() i
i ![]() są symetryczne i dodatnio określone.
są symetryczne i dodatnio określone.
Można pokazać, że macierz
![]() ma wartości własne ujemne o module od jeden do rzędu
ma wartości własne ujemne o module od jeden do rzędu ![]() ,
czyli bardzo dużym module dla małych
,
czyli bardzo dużym module dla małych ![]() . Zatem dla
. Zatem dla ![]() układ równań zwyczajnych jest sztywny
zgodnie z definicją z rozdziału 6.
Należy tu stosować schematy całkowania równań zwyczajnych stosowne do zadań sztywnych.
układ równań zwyczajnych jest sztywny
zgodnie z definicją z rozdziału 6.
Należy tu stosować schematy całkowania równań zwyczajnych stosowne do zadań sztywnych.
14.2.2. Przypadek dwuwymiarowy
Rozpatrzmy dwuwymiarowe modelowe zadanie na dowolnym obszarze wielokątnym na płaszczyźnie ![]() ,
czyli zastępując kwadrat przez
,
czyli zastępując kwadrat przez ![]() w (14.8).
Jego słabe sformułowanie otrzymujemy analogicznie jak w rozdziale 11, lub w przypadku jednowymiarowym (por. rozdział 14.2.1).
Mnożąc równanie paraboliczne z (14.8) przez funkcję testową z
w (14.8).
Jego słabe sformułowanie otrzymujemy analogicznie jak w rozdziale 11, lub w przypadku jednowymiarowym (por. rozdział 14.2.1).
Mnożąc równanie paraboliczne z (14.8) przez funkcję testową z ![]() ,
całkując po
,
całkując po ![]() i stosując wzory Greene'a otrzymujemy:
i stosując wzory Greene'a otrzymujemy:
dla ![]() ,
, ![]() oraz
oraz ![]() spełnia
warunek początkowy
spełnia
warunek początkowy ![]() .
.
Jak w rozdziale 14.2.1 otrzymujemy, że
powyższe równanie jest równoważne znalezieniu funkcji ![]() takiej, że
takiej, że
| (14.13) | |||||
dla ![]() , co jest słabym, wariacyjnym sformułowaniem (14.8),
które stanowi wyjście do konstrukcji dyskretyzacji
równania parabolicznego za pomocą metody elementu skończonego.
Rozpatrzmy
, co jest słabym, wariacyjnym sformułowaniem (14.8),
które stanowi wyjście do konstrukcji dyskretyzacji
równania parabolicznego za pomocą metody elementu skończonego.
Rozpatrzmy ![]() triangulacje równomierną
triangulacje równomierną ![]() , złożoną z przystających trójkątów, zdefiniowaną
jak w rozdziale 12 i
, złożoną z przystających trójkątów, zdefiniowaną
jak w rozdziale 12 i
![]() - przestrzeń funkcji ciągłych kawałkami liniowych na tej triangulacji, zerujących się na brzegu, czyli przestrzenią liniowego elementu skończonego
(por. rozdział 12).
- przestrzeń funkcji ciągłych kawałkami liniowych na tej triangulacji, zerujących się na brzegu, czyli przestrzenią liniowego elementu skończonego
(por. rozdział 12).
Dyskretyzację po przestrzeni zadania (14.13) definiujemy: znajdź funkcję ![]() taką, że dla
taką, że dla ![]() i dowolnego
i dowolnego ![]() :
:
| (14.14) | |||||
Otrzymaliśmy zatem ponownie układ równań zwyczajnych liniowych z warunkiem początkowym,
który po wprowadzeniu standardowej bazy daszkowej ![]() dla
dla ![]() , por. (12.1.2), możemy przepisać jako zadanie początkowe
na funkcje-współczynniki
, por. (12.1.2), możemy przepisać jako zadanie początkowe
na funkcje-współczynniki ![]() takie, że
takie, że ![]() .
Następnie to zadanie początkowe możemy rozwiązać za pomocą jakiegoś schematu, np. otwartego lub
zamkniętego schematu Eulera, lub schematu trapezów. Okazuje się, że - tak samo jak w
przypadku jednowymiarowym - dla
.
Następnie to zadanie początkowe możemy rozwiązać za pomocą jakiegoś schematu, np. otwartego lub
zamkniętego schematu Eulera, lub schematu trapezów. Okazuje się, że - tak samo jak w
przypadku jednowymiarowym - dla ![]() powstające układy równań zwyczajnych są sztywne.
Dlatego w praktyce stosuje się odpowiednie schematy dla zadań sztywnych.
powstające układy równań zwyczajnych są sztywne.
Dlatego w praktyce stosuje się odpowiednie schematy dla zadań sztywnych.
14.3. Zadania
Ćwiczenie 14.1
Zbadaj rzędy błędów aproksymacji otwartego schematu Eulera (14.1.1)
i zamkniętego schematu Eulera (14.1.1)
dla dyskretyzacji modelowego problemu jednowymiarowego w dyskretnej
normie maksimum przyjmując, że rozwiązanie jest dostatecznie gładkie.
Ustal, jaka minimalna gładkość rozwiązania jest konieczna, tzn.
znajdź najmniejsze ![]() takie, że jeśli rozwiązanie
takie, że jeśli rozwiązanie ![]() , to rząd aproksymacji schematu jest możliwie duży.
, to rząd aproksymacji schematu jest możliwie duży.
Ćwiczenie 14.2
Zbadaj stabilność zamkniętego schematu Eulera (14.1.1)
dla dyskretyzacji modelowego problemu jednowymiarowego w dyskretnej normie maksimum
dla ![]() . Wywnioskuj zbieżność dyskretną schematu w tejże normie.
. Wywnioskuj zbieżność dyskretną schematu w tejże normie.
Ćwiczenie 14.3
Zbadaj rząd błędu aproksymacji schematu Cranka-Nicholson dla ![]() dla dyskretyzacji modelowego problemu jednowymiarowego w dyskretnej normie maksimum
przyjmując, że rozwiązanie jest dostatecznie gładkie. Ustal, jaka minimalna gładkość rozwiązania jest konieczna,
aby schemat miał ten rząd. Zbadaj stabilność tego schematu w dyskretnej normie maksimum:
czy jest warunkowa, czy bezwarunkowa? Zbadaj zbieżność w dyskretnej normie maksimum.
dla dyskretyzacji modelowego problemu jednowymiarowego w dyskretnej normie maksimum
przyjmując, że rozwiązanie jest dostatecznie gładkie. Ustal, jaka minimalna gładkość rozwiązania jest konieczna,
aby schemat miał ten rząd. Zbadaj stabilność tego schematu w dyskretnej normie maksimum:
czy jest warunkowa, czy bezwarunkowa? Zbadaj zbieżność w dyskretnej normie maksimum.




