Zagadnienia
2. Równania różniczkowe - wprowadzenie
Przy pomocy równań różniczkowych modelowanych jest wiele różnych zagadnień. Równaniami różniczkowymi nazywamy takie równania, w których szukaną niewiadomą jest funkcja lub wektor funkcyjny, których pochodne i same funkcję muszą spełniać odpowiednie równania.
2.1. Równania różniczkowe zwyczajne
Najprostszą klasą równań są równania różniczkowe zwyczajne, (ang. ordinary differential equation), czyli równania postaci:
| (2.1) |
na funkcję ![]() dla
dla
![]() i
i ![]() zbioru otwartego w
zbioru otwartego w ![]() .
Takie równanie zwyczajne nazywamy równaniem rzędu
.
Takie równanie zwyczajne nazywamy równaniem rzędu ![]() .
.
Przy założeniu, że ![]() dla
dla
![]() ,
otrzymujemy równanie dające się rozwikłać względem
,
otrzymujemy równanie dające się rozwikłać względem ![]() , tzn.
istnieje funkcja
, tzn.
istnieje funkcja ![]() określona na otoczeniu
określona na otoczeniu ![]() punktu
punktu ![]() taka, że
taka, że
![]() na
na ![]() .
Zatem po rozwikłaniu otrzymujemy nowe równanie:
.
Zatem po rozwikłaniu otrzymujemy nowe równanie:
którego rozwiązaniem jest funkcja ![]() i które łatwiej numerycznie rozwiązać.
Od tej pory będziemy zakładać, że równanie różniczkowe jest w tej postaci. Więcej informacji na temat metod numerycznych rozwiązywania równań różniczkowych zwyczajnych podanych w sposób niejawny, tzn. w postaci (2.1) (zwanymi też równaniami różniczkowo-algebraicznymi) można znaleźć w
[1] lub [3].
i które łatwiej numerycznie rozwiązać.
Od tej pory będziemy zakładać, że równanie różniczkowe jest w tej postaci. Więcej informacji na temat metod numerycznych rozwiązywania równań różniczkowych zwyczajnych podanych w sposób niejawny, tzn. w postaci (2.1) (zwanymi też równaniami różniczkowo-algebraicznymi) można znaleźć w
[1] lub [3].
Zauważmy, że przez proste podstawienie
![]() i
i ![]() dla
dla ![]() otrzymujemy
nowy układ równań pierwszego rzędu:
otrzymujemy
nowy układ równań pierwszego rzędu:
![\begin{array}[]{l}\frac{dy_{1}}{dt}=y_{2}\\
\frac{dy_{2}}{dt}=y_{3}\\
\vdots\\
\frac{dy_{k}}{dt}=f_{1}(t,y_{1},\ldots,y_{k}),\end{array}](wyklady/nrr/mi/mi62.png) |
(2.2) |
który jest szczególnym równaniem pierwszego rzędu postaci:
| (2.3) |
gdzie funkcja ![]() jest zadaną funkcją ciągłą. Tutaj
jest zadaną funkcją ciągłą. Tutaj ![]() jest zbiorem otwartym.
jest zbiorem otwartym.
Zagadnieniem początkowym (zagadnieniem Cauchy'ego) nazywamy równanie z warunkiem początkowym:
| (2.4) |
gdzie ![]() jest ustalone.
jest ustalone.
Rozwiązaniem równania (2.3) nazwiemy funkcję ![]() klasy
klasy ![]() określoną na podzbiorze otwartym
określoną na podzbiorze otwartym ![]() taką, że
taką, że
Jeśli dodatkowo ![]() i
i ![]() , czyli
, czyli ![]() spełnia warunek początkowy to
spełnia warunek początkowy to ![]() jest rozwiązaniem zagadnienia początkowego (2.4).
W przyszłości często będziemy oznaczać rozwiązanie (2.3) jako
jest rozwiązaniem zagadnienia początkowego (2.4).
W przyszłości często będziemy oznaczać rozwiązanie (2.3) jako ![]() .
.
Podamy teraz kilka prostych przykładów zagadnień fizycznych, czy ogólnie przyrodniczych modelowanych równaniami różniczkowymi zwyczajnymi.
Przykład 2.1
Najprostszy model populacji danego gatunku zwierząt:
gdzie ![]() - stan populacji w momencie czasu
- stan populacji w momencie czasu ![]() i
i ![]() jest stałą większą od zera, szybkością namnażania się osobników, zależną od gatunku. Tu możemy podać rozwiązania
jest stałą większą od zera, szybkością namnażania się osobników, zależną od gatunku. Tu możemy podać rozwiązania
![]() .
.
Oczywiście ten model jest nierealistyczny, ponieważ populacja - nawet izolowana - nie może rosnąc do nieskończoności. Podajmy więc bardziej skomplikowany model wzrostu logistycznego:
Przykład 2.2
Model logistyczny populacji.
gdzie ![]() są stałymi większymi od zera.
są stałymi większymi od zera. ![]() oznacza pojemność populacji, czy górną granicę populacji.
Tu też możemy podać rozwiązania, ale pozostawimy to jako zadanie.
oznacza pojemność populacji, czy górną granicę populacji.
Tu też możemy podać rozwiązania, ale pozostawimy to jako zadanie.
Przykład 2.3
Rozpad radioaktywnego węgla. Wiemy, że w czasie ![]() połowa atomów węgla rozpada się. Ilość
atomów modelowana jest równaniem:
połowa atomów węgla rozpada się. Ilość
atomów modelowana jest równaniem:
gdzie ![]() jest szybkością rozpadu, stałą większą od zera. Rozwiązaniem tego równania jest
jest szybkością rozpadu, stałą większą od zera. Rozwiązaniem tego równania jest ![]() .
.
Przykład 2.4
Równanie Newtona.
Rozpatrzmy ruch cząsteczki w przestrzeni. Oznaczmy wektory:
-
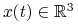 położenie cząsteczki w przestrzeni w czasie
położenie cząsteczki w przestrzeni w czasie 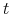 ,
, -
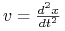 prędkość cząsteczki,
prędkość cząsteczki, -
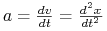 pochodna prędkości, czyli druga pochodna położenia, tj. przyspieszenie.
pochodna prędkości, czyli druga pochodna położenia, tj. przyspieszenie.
Jeśli ruch cząsteczki sterowany jest jakąś zewnętrzną siłą
to - zgodnie z prawem dynamiki Newtona - zachodzi następujący związek:
gdzie ![]() jest masą cząsteczki.
W ten sposób otrzymaliśmy równanie różniczkowe zwane równaniem Newtona:
jest masą cząsteczki.
W ten sposób otrzymaliśmy równanie różniczkowe zwane równaniem Newtona:
Jeśli dodatkowo znamy położenie i prędkości cząsteczki, tzn. ![]() i
i ![]() w danym momencie czasu, to
możemy wyznaczyć jej położenie po jakimś czasie.
w danym momencie czasu, to
możemy wyznaczyć jej położenie po jakimś czasie.
W najprostszym przypadku załóżmy, że działa siła grawitacji skierowana w dół, czyli wzdłuż osi ![]() (jest to duże uproszczenie, ale dość dobrze modeluje ruch):
tzn. siła stała
(jest to duże uproszczenie, ale dość dobrze modeluje ruch):
tzn. siła stała ![]() . Otrzymujemy wówczas równanie
. Otrzymujemy wówczas równanie
![\begin{array}[]{l}\frac{d^{2}x_{1}}{dt^{2}}=0\\
\frac{d^{2}x_{2}}{dt^{2}}=0\\
\frac{d^{2}x_{3}}{dt^{2}}=-m\, g.\\
\end{array}](wyklady/nrr/mi/mi208.png) |
Znając położenie i prędkość w chwili ![]() łatwo je rozwiązać:
łatwo je rozwiązać:
![]() ,
, ![]() i
i ![]() .
.
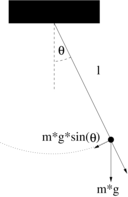
Przykład 2.5
Równanie wahadła.
Wyprowadzamy równanie zgodnie z Rysunkiem 2.2.
Ruch powoduje siła ![]() , gdzie
, gdzie ![]() jest masą,
jest masą, ![]() to przyspieszenie ziemskie,
a
to przyspieszenie ziemskie,
a ![]() jest kątem wychylenia się wahadła.
Długość łuku:
jest kątem wychylenia się wahadła.
Długość łuku:
gdzie ![]() to długość wahadła,
stąd
to długość wahadła,
stąd
zatem otrzymujemy równanie:
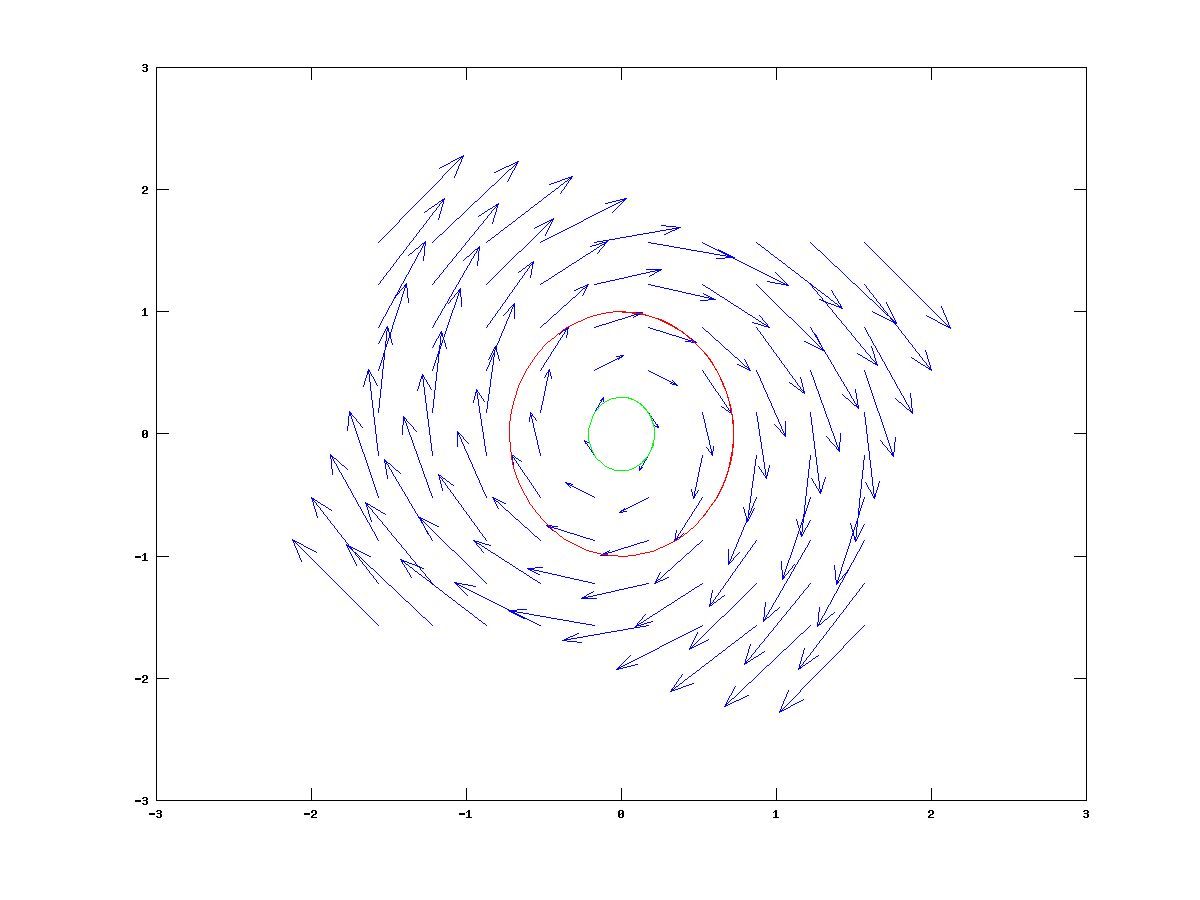
Sprowadzając je do równania pierwszego rzędu otrzymujemy:
Możemy naszkicować pole wektorowe tego równania. Tzn. ogólnie jakakolwiek trajektoria rozwiązania ![]() jest styczna do pola wektorowego zadanego przez prawą stronę równania
jest styczna do pola wektorowego zadanego przez prawą stronę równania ![]() , czyli
w naszym przypadku pole wektorowe w punkcie
, czyli
w naszym przypadku pole wektorowe w punkcie ![]() przyjmuje wartość
przyjmuje wartość ![]() ,
por. Rysunek 2.3.
,
por. Rysunek 2.3.
2.2. Równania różniczkowe cząstkowe
Ogólnie mówiąc, równania różniczkowe cząstkowe to równania, których rozwiązania są funkcjami wielu zmiennych, i w których pojawiają się pochodne cząstkowe. Przy niektórych typach równań wyróżnia się jedną ze zmiennych i oznacza jako czas ![]() ; o takich równaniach mówimy często jako o równaniach ewolucyjnych.
; o takich równaniach mówimy często jako o równaniach ewolucyjnych.
W tym rozdziale wymienimy podstawowe typy równań różniczkowych cząstkowych, które pojawią się w treści tego skryptu.
Po więcej informacji na temat podstawowych idei i pojęć dotyczących dziedziny matematyki zwanej równaniami różniczkowymi cząstkowymi odsyłamy do obszernego podręcznika Lawrence'a Evansa [11].
2.2.1. Równania eliptyczne
W przypadku równań eliptycznych nie mamy wyróżnionej zmiennej, ponieważ opisują one często stany stacjonarne zjawisk fizycznych.
Podstawowym przykładem równania eliptycznego jest
równanie Laplace'a:
gdzie ![]() i
i ![]() jest obszarem.
jest obszarem.
Jeśli dołożymy warunek brzegowy, to otrzymamy klasyczne równanie Poissona.
Szukamy tu ![]() takiego, że
takiego, że
| (2.5) |
Zagadnienie z laplasjanem może mieć też inne warunki brzegowe.
To jest podstawowy przykład zagadnienia eliptycznego, zwanego też zagadnieniem stacjonarnym, czy zagadnieniem brzegowym.
W szczególności równanie Laplace'a modeluje rozkład potencjału elektrycznego w ![]() .
.
Zachodzi prawo fizyczne Gaussa:
gdzie ![]() - to operator dywergencji (rozbieżności) pola,
- to operator dywergencji (rozbieżności) pola, ![]() - to natężenie pola elektrycznego,
- to natężenie pola elektrycznego, ![]() - to gęstość ładunku elektrycznego,
- to gęstość ładunku elektrycznego, ![]() - to przenikalność elektryczna.
- to przenikalność elektryczna.
Minus gradient potencjału ![]() daje natężenie pola elektrycznego, tzn.
daje natężenie pola elektrycznego, tzn.
z tego wynika, że otrzymujemy
Jeśli ładunek równy zero, to otrzymujemy równanie Laplace'a:
Podamy teraz ogólniejszą definicję równania (operatora) eliptycznego drugiego rzędu.
Rozważmy równanie różniczkowe liniowe drugiego rzędu dla ogólnego operatora liniowego drugiego rzędu ![]() ,
określonego dla
,
określonego dla ![]() dla
dla ![]() :
:
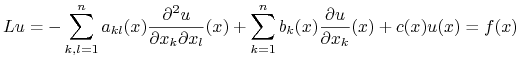 |
(2.6) |
gdzie ![]() są danymi funkcjami (zazwyczaj ciągłymi) określonymi na obszarze
są danymi funkcjami (zazwyczaj ciągłymi) określonymi na obszarze ![]() .
.
Definicja 2.1
Równanie (2.6) (operator ![]() ) jest
eliptyczne w punkcie
) jest
eliptyczne w punkcie ![]() , gdy macierz
, gdy macierz ![]() jest dodatnio określona: tzn.:
jest dodatnio określona: tzn.:
Operator ![]() jest eliptyczny w obszarze
jest eliptyczny w obszarze ![]() jeśli
jeśli ![]() jest eliptyczny w każdym punkcie obszaru
jest eliptyczny w każdym punkcie obszaru ![]() .
.
Warto wspomnieć, że w praktyce pojawiają się także równania eliptyczne czwartego rzędu, np. równanie bi-harmoniczne, które modeluje np. wygiętą cienką membranę (czy płytkę) poprzez zewnętrzną siłę:
gdzie
![]() - to operator bi-harmoniczny,
- to operator bi-harmoniczny, ![]() - to odchylenie membrany od położenia zero,
- to odchylenie membrany od położenia zero, ![]() - to siła wyginająca membranę pionowo do góry.
Tutaj też mogą zachodzić warunki brzegowe różnego typu:
- to siła wyginająca membranę pionowo do góry.
Tutaj też mogą zachodzić warunki brzegowe różnego typu:
dla płytki przygiętej (tutaj ![]() - to wektor normalny zewnętrzny do brzegu
- to wektor normalny zewnętrzny do brzegu ![]() ), czy
), czy
dla zadania podpartej płytki.
2.2.2. Równania hiperboliczne pierwszego rzędu
Ogólnie za równanie różniczkowe hiperboliczne pierwszego rzędu uważamy równanie postaci:
dla funkcji ![]() i obszaru
i obszaru ![]() .
.
Dodatkowo dodaje się warunek brzegowy na brzegu lub części brzegu ![]() np.:
np.:
gdzie ![]() - to dana funkcja.
- to dana funkcja.
Będą nas w szczególności interesować równania liniowe:
| (2.7) |
dla danych funkcji ![]() .
.
Ważnym przykładem jest równanie:
gdzie ![]() - to stała, dla którego znamy rozwiązanie:
- to stała, dla którego znamy rozwiązanie:
dla dowolnej funkcji różniczkowalnej w sposób ciągły ![]() .
.
Dodając warunek początkowy
dla ![]() otrzymujemy jednoznaczne rozwiązanie
otrzymujemy jednoznaczne rozwiązanie
2.2.3. Równania hiperboliczne drugiego rzędu
Ogólnie równaniem liniowym hiperbolicznym drugiego rzędu nazwiemy równanie:
| (2.8) |
dla operatora ![]() eliptycznego w
eliptycznego w ![]() .
Tutaj
.
Tutaj ![]() .
.
Klasycznym przykładem takiego równania jest równanie falowe:
Dla prawej strony równej zero, tj. ![]() , nazywamy je jednorodnym równaniem falowym, a w przeciwnym przypadku nazywamy je niejednorodnym równaniem falowym.
, nazywamy je jednorodnym równaniem falowym, a w przeciwnym przypadku nazywamy je niejednorodnym równaniem falowym.
Odpowiada ono drganiu struny (![]() , membrany (
, membrany (![]() ) i elastycznej bryły (
) i elastycznej bryły (![]() ).
Wartości
).
Wartości ![]() odpowiadają położeniu np. struny w momencie czasu
odpowiadają położeniu np. struny w momencie czasu ![]() , jako że
zmienna
, jako że
zmienna ![]() odpowiada czasowi - jest to równanie ewolucyjne.
odpowiada czasowi - jest to równanie ewolucyjne.
Aby zadanie posiadało jednoznaczne rozwiązanie należy:
-
Podać warunki brzegowe np. typu Dirichleta
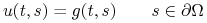
dla danej funkcji
![g:[0,T]\times\partial\Omega\rightarrow\mathbb{R}](wyklady/nrr/mi/mi17.png) . Zakładamy, że na brzegu znamy położenie struny.
Gdyby
. Zakładamy, że na brzegu znamy położenie struny.
Gdyby 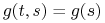 , to struna czy membrana byłaby zaczepiona.
, to struna czy membrana byłaby zaczepiona. -
Podać warunki początkowe:
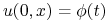
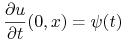
dla danych funkcji określonych na
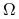 . Warunki początkowe oznaczają, że znamy położenie i prędkości np. struny w momencie startowym
. Warunki początkowe oznaczają, że znamy położenie i prędkości np. struny w momencie startowym 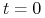 .
.
2.2.4. Równania paraboliczne
Równaniem liniowym parabolicznym drugiego rzędu nazywamy równanie:
| (2.9) |
gdzie ![]() operator eliptyczny w
operator eliptyczny w ![]() .
.
Klasycznym równaniem parabolicznym jest równanie przewodnictwa ciepła:
opisujące rozchodzenie się ciepła w pręcie (![]() ), cienkiej płytce (
), cienkiej płytce (![]() ), czy bryle (
), czy bryle (![]() ).
Wartości
).
Wartości ![]() odpowiadają temperaturze w punkcie
odpowiadają temperaturze w punkcie ![]() w momencie czasu
w momencie czasu ![]() . Jest to równanie ewolucyjne.
Aby zadanie było dobrze postawione należy dodać warunek początkowy
. Jest to równanie ewolucyjne.
Aby zadanie było dobrze postawione należy dodać warunek początkowy
![]() w
w ![]() oraz warunki brzegowe np. typu Dirichleta
oraz warunki brzegowe np. typu Dirichleta
dla danej funkcji ![]() co oznacza, że znamy temperaturę na brzegu
i temperaturę początkową:
co oznacza, że znamy temperaturę na brzegu
i temperaturę początkową:
dla danej funkcji ![]() określonej na
określonej na ![]() .
.
Możemy też na brzegu ![]() postawić inne warunki brzegowe np. z pochodną, które odpowiadają temu, że znamy strumień energii wpływającej do płytki, czyli
postawić inne warunki brzegowe np. z pochodną, które odpowiadają temu, że znamy strumień energii wpływającej do płytki, czyli
W jednym wymiarze, tzn. dla ![]() i dla równania ze współczynnikiem stałym
i dla równania ze współczynnikiem stałym ![]() i
i
![]() , warunkami brzegowymi
, warunkami brzegowymi ![]() i warunkiem początkowym
i warunkiem początkowym ![]() tzn.:
tzn.:
znamy rozwiązanie:
![]() czyli rozwiązanie gaśnie wraz z upływem czasu.
czyli rozwiązanie gaśnie wraz z upływem czasu.
2.3. Zadania
Ćwiczenie 2.1
Rozpatrzmy zadanie początkowe autonomiczne (tzn. prawa strona równania nie zależy od ![]() ):
):
dla ![]() ,
, ![]() - to obszar,
i
- to obszar,
i ![]() dla pewnego
dla pewnego ![]() .
Pokaż, że istnieje otoczenie
.
Pokaż, że istnieje otoczenie ![]() punktu
punktu
![]() takie, że na tym otoczeniu równanie
takie, że na tym otoczeniu równanie
ma rozwiązania ![]() takie, że krzywa całkowa tego równania,
tzn. zbiór
takie, że krzywa całkowa tego równania,
tzn. zbiór ![]() zawarta jest w trajektorii wyjściowego równania, tzn. w zbiorze
zawarta jest w trajektorii wyjściowego równania, tzn. w zbiorze
![]() dla
dla ![]() rozwiązań wyjściowego równania.
rozwiązań wyjściowego równania.
Z tego, że ![]() i z twierdzenia o funkcji odwrotnej wynika, że istnieje
otoczenie
i z twierdzenia o funkcji odwrotnej wynika, że istnieje
otoczenie ![]() , na którym określona jest funkcja
, na którym określona jest funkcja ![]() odwrotna do
odwrotna do ![]() , której pochodna równa się
, której pochodna równa się ![]() . Wtedy szukaną funkcją jest
złożeniem
. Wtedy szukaną funkcją jest
złożeniem ![]() i
i ![]() , czyli
, czyli ![]() i zawieranie się krzywej całkowej w trajektorii jest oczywiste.
i zawieranie się krzywej całkowej w trajektorii jest oczywiste.
Ćwiczenie 2.2
Wyprowadź równania ruchu wahadła w postaci:
dla ![]() położenia wahadła (przyjmujemy, że dla
położenia wahadła (przyjmujemy, że dla ![]() zachodzi
zachodzi ![]() ).
).
Narysuj powyższe pole wektorowe wahadła w Octavie (funkcja quiver()).
Trzeba dokonać rozkładu na odpowiednie składowe jedynej siły, która powoduje ruch wahadła
czyli ![]() stycznej do toru ruchu. Następnie skorzystać z tego jak wyraża się położenie
punktu w terminach
stycznej do toru ruchu. Następnie skorzystać z tego jak wyraża się położenie
punktu w terminach ![]() .
.
Zauważmy, że ![]() i siła działająca poziomo jest równa
i siła działająca poziomo jest równa
![]() a działająca pionowo:
a działająca pionowo: ![]() .
.
Ćwiczenie 2.3 (Metoda Fouriera)
Rozważmy równanie paraboliczne jednowymiarowe:
z warunkami brzegowymi ![]() i początkowym
i początkowym
![]() .
Załóżmy, że szukamy rozwiązania postaci:
.
Załóżmy, że szukamy rozwiązania postaci:
Wstaw ![]() takiej postaci do powyższego równania i pokaż, że dostajemy
dwa niezależne równania różniczkowe zwyczajne na
takiej postaci do powyższego równania i pokaż, że dostajemy
dwa niezależne równania różniczkowe zwyczajne na ![]() i
i ![]() .
Rozwiąż te równania tzn. znajdź rozwiązania uogólnione i sprawdź dla jakich
.
Rozwiąż te równania tzn. znajdź rozwiązania uogólnione i sprawdź dla jakich
![]() możemy wyznaczyć rozwiązanie wyjściowego problemu.
możemy wyznaczyć rozwiązanie wyjściowego problemu.
Ćwiczenie 2.4 (Metoda Fouriera)
Rozważmy równanie hiperboliczne jednowymiarowe:
z warunkami brzegowymi ![]() i początkowymi
i początkowymi
![]() i
i ![]() .
Załóżmy, że szukamy rozwiązania postaci:
.
Załóżmy, że szukamy rozwiązania postaci:
Wstaw ![]() takiej postaci do powyższego równania i pokaż, że dostajemy
dwa niezależne równania różniczkowe zwyczajne na
takiej postaci do powyższego równania i pokaż, że dostajemy
dwa niezależne równania różniczkowe zwyczajne na ![]() i
i ![]() .
Rozwiąż te równania, tzn. znajdź rozwiązania uogólnione, czyli rodzinę rozwiązań zależną od stałej, i sprawdź dla jakich
.
Rozwiąż te równania, tzn. znajdź rozwiązania uogólnione, czyli rodzinę rozwiązań zależną od stałej, i sprawdź dla jakich
![]() możemy wyznaczyć rozwiązanie wyjściowego problemu.
możemy wyznaczyć rozwiązanie wyjściowego problemu.
Ćwiczenie 2.5 (Metoda charakterystyk)
Rozpatrzmy równanie różniczkowe pierwszego rzędu ![]() dla funkcji
dla funkcji
![]() i
i ![]() .
Przyjmijmy, że szukamy krzywych
.
Przyjmijmy, że szukamy krzywych ![]() na których można wyznaczyć
rozwiązanie.
Przyjmijmy oznaczenia
na których można wyznaczyć
rozwiązanie.
Przyjmijmy oznaczenia
Różniczkując ostatnie równanie otrzymujemy:
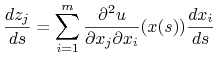 |
(2.10) |
a różniczkując po ![]() wyjściowe równanie widzimy, że
wyjściowe równanie widzimy, że
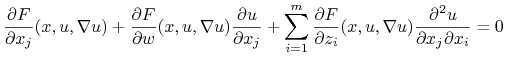 |
(2.11) |
Treścią zadania jest wykazanie, że definiując krzywą ![]() jako krzywą spełniającą równanie:
jako krzywą spełniającą równanie:
| (2.12) |
i korzystając z powyższych równań
otrzymujemy, że ![]() spełniają następujący układ równań zwyczajnych:
spełniają następujący układ równań zwyczajnych:
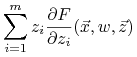 |
||||
Równania te nazywamy równaniami charakterystyk dla wyjściowego równania pierwszego rzędu, a krzywe
![]() - charakterystykami tego równania.
- charakterystykami tego równania.
Ćwiczenie 2.6
Wyprowadź równania charakterystyk dla równań liniowych pierwszego rzędu (2.7) jednorodnych tzn. z ![]() .
Oblicz rozwiązania dla równania liniowego w dwóch wymiarach dla
.
Oblicz rozwiązania dla równania liniowego w dwóch wymiarach dla ![]() i
i ![]() stałej,
stałej, ![]() i warunku brzegowego
i warunku brzegowego ![]() dla
dla ![]() .
.