Zagadnienia
3. Metody dla równań różniczkowych zwyczajnych
W tym i kilku następnych rozdziałach zajmiemy się schematami rozwiązywania równań różniczkowych zwyczajnych. Ten rozdział jest poświęcony wprowadzeniu najprostszych metod (schematów) rozwiązywania równań różniczkowych zwyczajnych.
3.1. Wprowadzenie
Załóżmy, że rozpatrujemy zagadnienie początkowe pierwszego rzędu (zagadnienie Cauchy'ego) :
| (3.1) |
gdzie ![]() ,
, ![]() jest funkcją ciągłą, a
jest funkcją ciągłą, a ![]() jest ustalone.
jest ustalone.
Z ogólnej teorii równań różniczkowych, por. [23] wiadomo, że
Twierdzenie 3.1 (Peano)
Jeśli ![]() jest funkcją ciągłą na otoczeniu
jest funkcją ciągłą na otoczeniu ![]() , to istnieje rozwiązanie (3.1) określone na pewnym otoczeniu
, to istnieje rozwiązanie (3.1) określone na pewnym otoczeniu ![]() .
.
Jeśli dodatkowo założymy, że ![]() jest funkcją lipschitzowska na otoczeniu
jest funkcją lipschitzowska na otoczeniu ![]() względem zmiennej
względem zmiennej ![]() , to
możemy pokazać jednoznaczności rozwiązania, tzn. zachodzi twierdzenie:
, to
możemy pokazać jednoznaczności rozwiązania, tzn. zachodzi twierdzenie:
Twierdzenie 3.2 (Picarda-Lindelöfa)
Jeśli ![]() jest funkcją ciągłą na otoczeniu
jest funkcją ciągłą na otoczeniu ![]() oraz
oraz ![]() jest funkcją lipschizowską względem
jest funkcją lipschizowską względem ![]() w pewnej kuli
w pewnej kuli ![]() , tzn.
, tzn.
to istnieje ![]() i
i ![]() takie, że
takie, że
![]() jest jednoznacznym rozwiązaniem (3.1).
jest jednoznacznym rozwiązaniem (3.1).
Od tej pory będziemy przyjmować, że funkcja ![]() , zwana też polem wektorowym, spełnia założenia twierdzenia Picarda-Lindelöfa, tzn. Twierdzenia 3.2, czyli że istnieje jednoznaczne rozwiązanie zadania Cauchy'ego na odcinku
, zwana też polem wektorowym, spełnia założenia twierdzenia Picarda-Lindelöfa, tzn. Twierdzenia 3.2, czyli że istnieje jednoznaczne rozwiązanie zadania Cauchy'ego na odcinku ![]() .
.
Zauważmy, że każde rozwiązanie jest krzywą styczną do pola wektorowego.
3.2. Równania liniowe ze stałymi współczynnikami
W tym podrozdziale krótko przypomnimy teorie dla ważnej klasy równań różniczkowych zwyczajnych, tzn. jednorodnych równań liniowych ze stałymi współczynnikami, czyli równań postaci:
gdzie ![]() - to stała macierz
- to stała macierz ![]() ,
dla których znamy rozwiązania zadania Cauchy'ego:
,
dla których znamy rozwiązania zadania Cauchy'ego:
| (3.2) |
Znamy wzór na rozwiązanie tego zadania:
gdzie eksponent od macierzy zdefiniowany jest wzorem
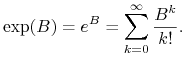 |
Skorzystamy ze znajomości postaci rozwiązania tej klasy równań w rozdziale 6.
W zależności od postaci Jordana macierzy ![]() można wypisać
postać
można wypisać
postać ![]() , w szczególności jeśli
macierz
, w szczególności jeśli
macierz ![]() jest diagonalizowalna,
tzn. istnieje baza wektorów własnych, które zapisane jako kolumny macierzy
jest diagonalizowalna,
tzn. istnieje baza wektorów własnych, które zapisane jako kolumny macierzy ![]() dają:
dają:
gdzie ![]() - to macierz diagonalna z wartościami własnymi macierzy
- to macierz diagonalna z wartościami własnymi macierzy ![]() na diagonali:
na diagonali:
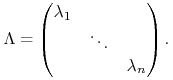 |
Wtedy wiadomo, że
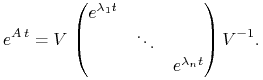 |
W szczególności jeśli ![]() dla wszystkich
dla wszystkich ![]() to
każde rozwiązanie spełnia
to
każde rozwiązanie spełnia
a z kolei jeśli istnieje ![]() takie, że
takie, że ![]() ,
to istnieje rozwiązanie zagadnienia Cauchy'go z niezerowym warunkiem brzegowym, dla którego
,
to istnieje rozwiązanie zagadnienia Cauchy'go z niezerowym warunkiem brzegowym, dla którego
3.3. Kilka prostych schematów
Załóżmy, że rozpatrujemy zadanie skalarne tzn. ![]() .
Chcemy w jakiś sposób przybliżyć rozwiązanie równania (3.1).
Przybliżamy pochodną poprzez iloraz różnicowy dla pewnego parametru
.
Chcemy w jakiś sposób przybliżyć rozwiązanie równania (3.1).
Przybliżamy pochodną poprzez iloraz różnicowy dla pewnego parametru ![]() :
:
i otrzymujemy otwarty schemat Eulera:
czy inaczej:
znając rozwiązanie w punkcie ![]()
![]() możemy
wyznaczyć przybliżone rozwiązanie
możemy
wyznaczyć przybliżone rozwiązanie ![]() w kolejnych punktach
w kolejnych punktach ![]() z powyższego wzoru.
Ale można też przybliżyć pochodną biorąc parametr
z powyższego wzoru.
Ale można też przybliżyć pochodną biorąc parametr ![]() w tył:
w tył:
i wtedy zastępując pochodną przez taki iloraz otrzymujemy zamknięty schemat Eulera:
czy inaczej:
Proszę zauważyć, że jeśli znamy rozwiązanie w punkcie ![]() , tzn.
, tzn. ![]() , to aby wyznaczyć kolejne przybliżenia rozwiązania w punktach
, to aby wyznaczyć kolejne przybliżenia rozwiązania w punktach ![]() należy rozwiązać
równania postaci:
należy rozwiązać
równania postaci:
| (3.3) |
względem ![]() , co sprawia, że zamknięty schemat Eulera może wydać się mało praktyczny w porównaniu z otwartym schematem Eulera. Dla niektórych równań jest to pozorne. Zauważmy tylko, że im
, co sprawia, że zamknięty schemat Eulera może wydać się mało praktyczny w porównaniu z otwartym schematem Eulera. Dla niektórych równań jest to pozorne. Zauważmy tylko, że im ![]() mniejsze, tym potencjalnie równanie (3.3)
jest łatwiejsze do rozwiązania (dlaczego?). Przyjrzymy się temu problemowi dokładniej w kolejnych rozdziałach.
mniejsze, tym potencjalnie równanie (3.3)
jest łatwiejsze do rozwiązania (dlaczego?). Przyjrzymy się temu problemowi dokładniej w kolejnych rozdziałach.
W dalszej części wykładu założymy, że chcemy przybliżyć rozwiązanie
![]() na odcinku
na odcinku ![]() , na którym
, na którym ![]() , w dyskretnych punktach czasu:
, w dyskretnych punktach czasu:
Często będziemy opuszczali indeks ![]() , o ile to nie będzie powodowało niejasności.
Wartość rozwiązania w punkcie
, o ile to nie będzie powodowało niejasności.
Wartość rozwiązania w punkcie ![]() , czyli
, czyli ![]() będzie przybliżana przez
będzie przybliżana przez
![]() , spełniające odpowiedni schemat.
Wygodnie jest też oznaczać
, spełniające odpowiedni schemat.
Wygodnie jest też oznaczać ![]() .
Górny indeks
.
Górny indeks ![]() będziemy często opuszczali, jeśli
będziemy często opuszczali, jeśli ![]() będzie ustalone.
będzie ustalone.
Tak więc otwarty schemat Eulera możemy zapisać jako:
| (3.4) |
a zamknięty schemat Eulera możemy zapisać jako:
| (3.5) |
Kolejnym wyprowadzeniem otwartego schematu Eulera (3.4) jest obcięcie rozwinięcia szeregu Taylora rozwiązania:
| (3.6) |
Zostawiamy tylko pierwsze dwa człony i otrzymujemy
czyli wstawiając ![]() za przybliżenie
za przybliżenie ![]() , a
, a ![]() za przybliżenie
za przybliżenie ![]() otrzymujemy znów otwarty schemat Eulera (3.4).
Analogicznie możemy wyprowadzić zamknięty schemat Eulera (3.5) rozwijając rozwiązanie w
otrzymujemy znów otwarty schemat Eulera (3.4).
Analogicznie możemy wyprowadzić zamknięty schemat Eulera (3.5) rozwijając rozwiązanie w ![]() dla
dla ![]() .
.
Jeszcze innym intuicyjnym wyprowadzeniem schematu otwartego Eulera jest
podążanie za
polem wektorowym.
Jak wiemy, wykresem rozwiązania równania różniczkowego jest
krzywa styczna do zadanego pola wektorowego ![]() spełniająca odpowiedni warunek początkowy.
Zatem znając rozwiązanie przybliżone dla
spełniająca odpowiedni warunek początkowy.
Zatem znając rozwiązanie przybliżone dla ![]() tzn. mając
tzn. mając ![]() , możemy wyznaczyć
, możemy wyznaczyć ![]() ,
przybliżenie rozwiązania
,
przybliżenie rozwiązania ![]() , biorąc poprawkę w kierunku pola wektorowego tzn.:
, biorąc poprawkę w kierunku pola wektorowego tzn.:
Czyli znów otrzymujemy otwarty schemat Eulera.
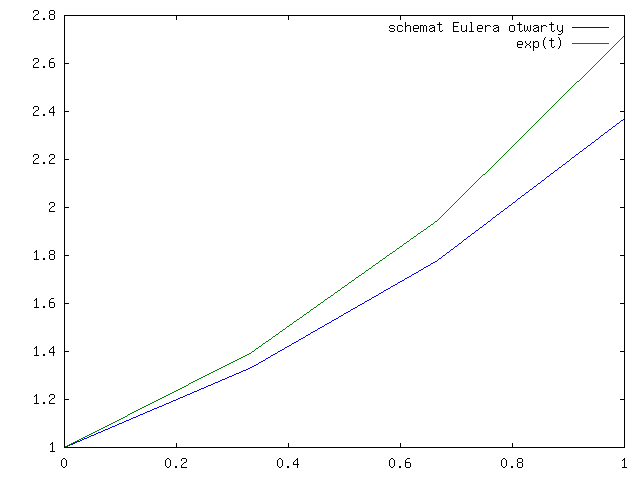
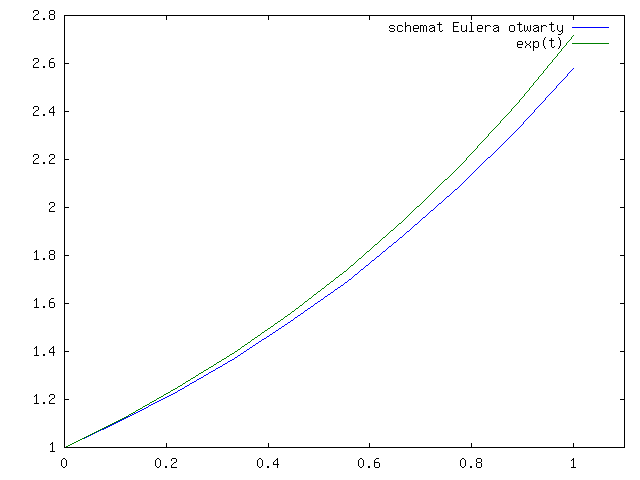
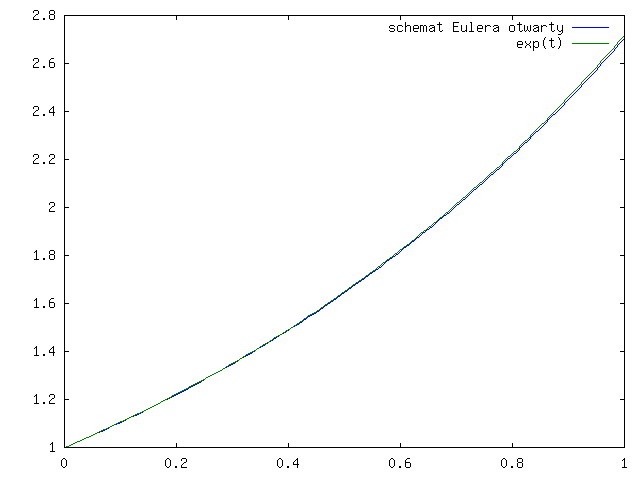
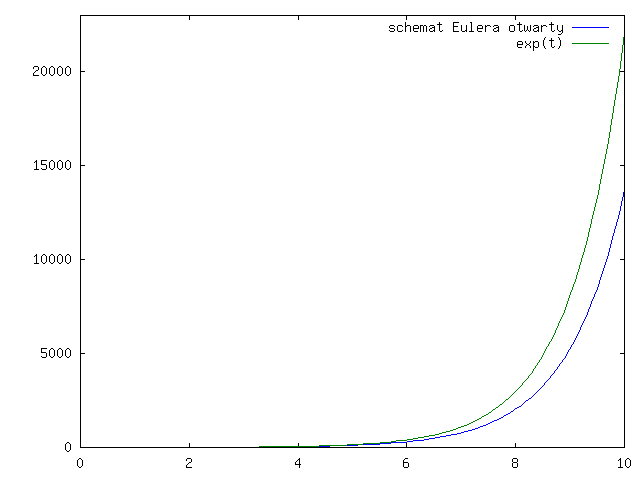
Zadajmy pytanie, czy takie schematy są wystarczająco dokładne. Czy one działają stabilnie na dłuższych odcinkach czasu, na których istnieje rozwiązanie?
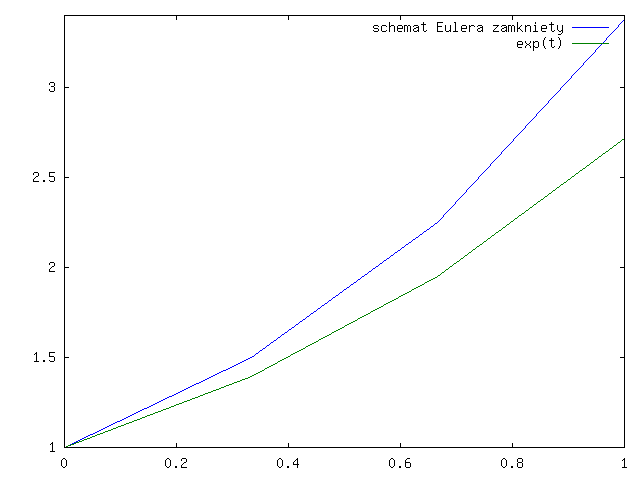
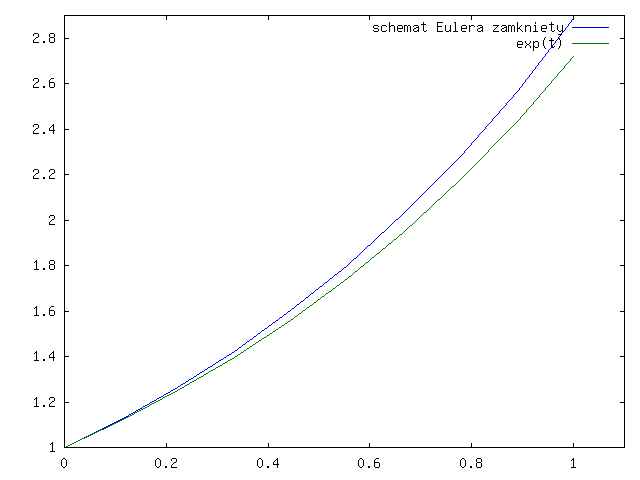
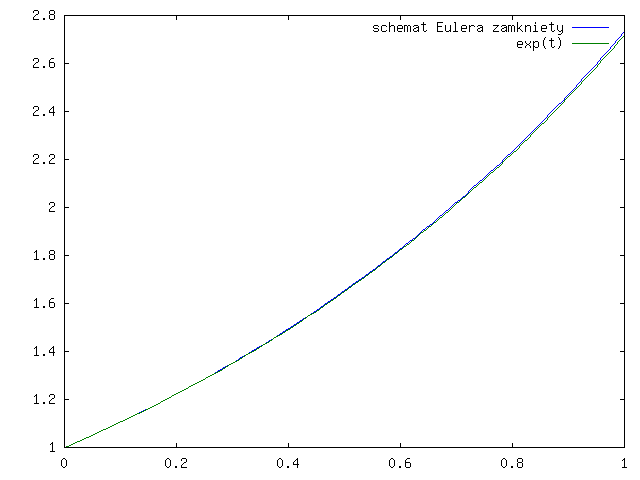
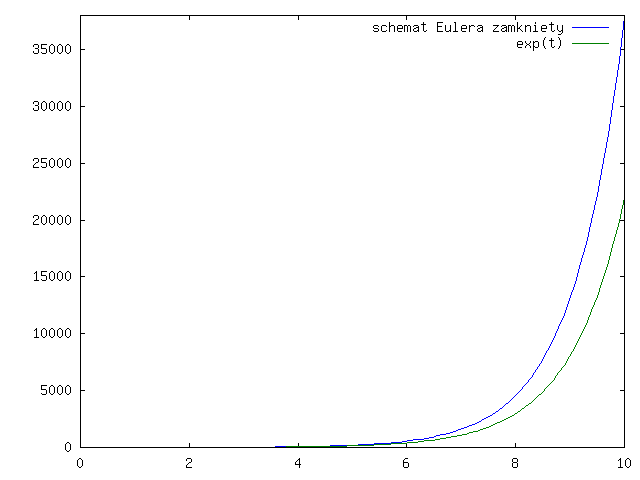
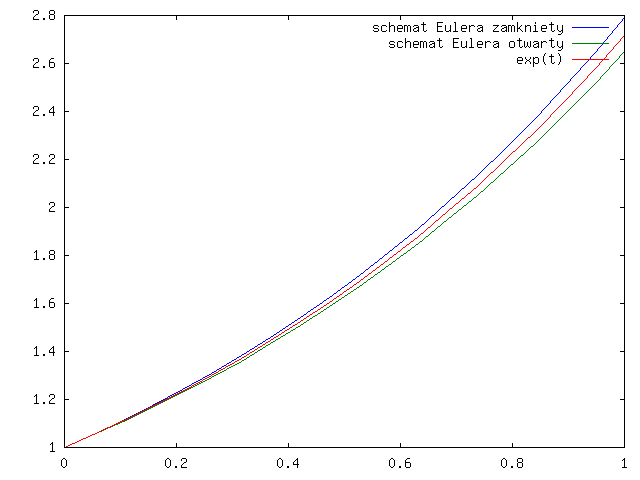
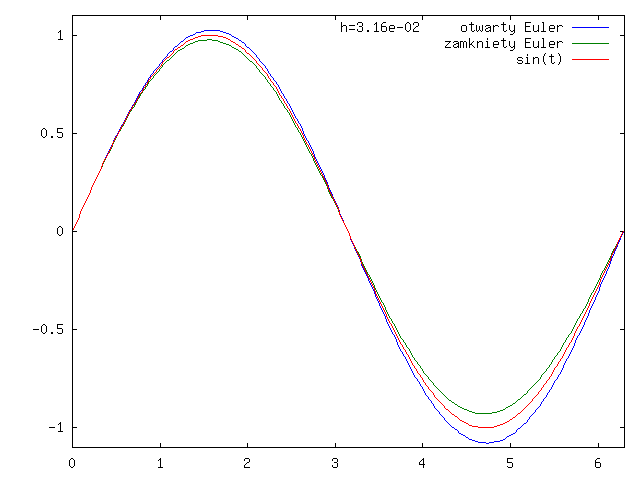
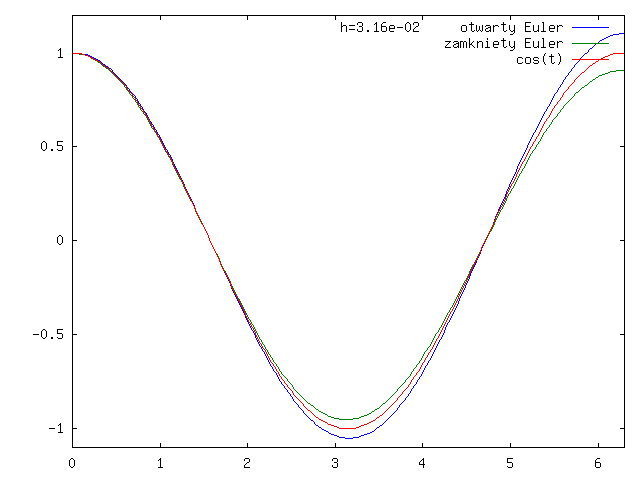
Sprawdźmy, co się dzieje dla modelowego zadania:
którego rozwiązaniem jest ![]() .
.
Otwarty schemat Eulera daje nam ciąg:
Ustalmy ![]() , czyli
, czyli ![]() . Wtedy
. Wtedy
Dla zamkniętego schematu Eulera otrzymujemy analogicznie:
czyli
Popatrzmy jak te dwa schematy działają (w praktyce) na wykresach dla ![]() i
i
![]() , por.
rysunki 3.1 - 3.4 dla
otwartego schematu Eulera
i rysunki 3.5 - 3.8 dla zamkniętego schematu Eulera.
, por.
rysunki 3.1 - 3.4 dla
otwartego schematu Eulera
i rysunki 3.5 - 3.8 dla zamkniętego schematu Eulera.
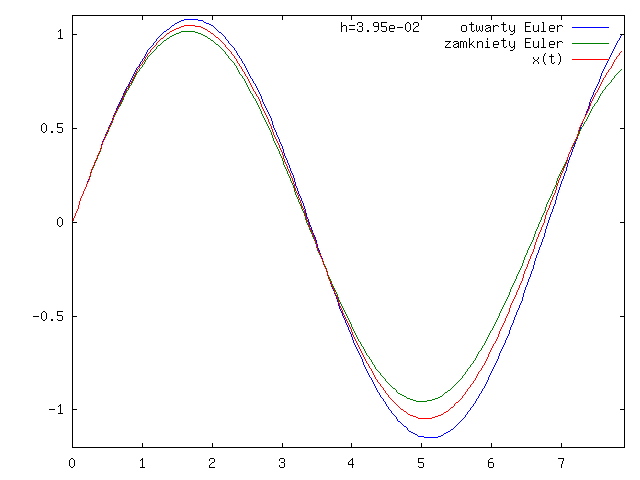
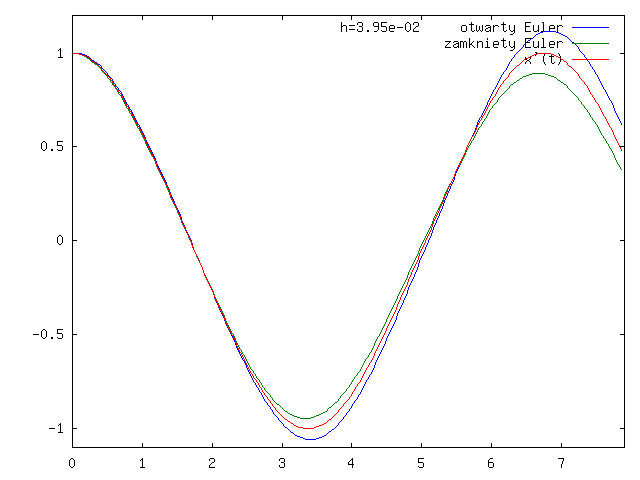
Zauważmy, że wykres rozwiązania ze schematu Eulera otwartego jest poniżej wykresu dokładnego rozwiązania, a dla schematu zamkniętego - powyżej, co widać lepiej na rysunku 3.9.
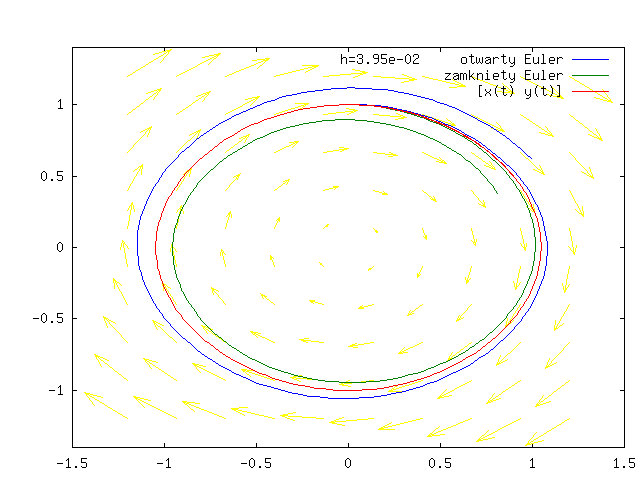
Popatrzmy na przypadek dwuwymiarowy.
Weźmy modelowe zadanie wahadła. Dla małych prędkości możemy przyjąć, że ![]() ,
stąd otrzymujemy równanie liniowe ze stałymi współczynnikami (zlinearyzowane równanie wahadła):
,
stąd otrzymujemy równanie liniowe ze stałymi współczynnikami (zlinearyzowane równanie wahadła):
gdzie ![]() to prędkość kątowa, a
to prędkość kątowa, a ![]() dla
dla ![]() wartości przyspieszenia
ziemskiego i l długości wahadła.
wartości przyspieszenia
ziemskiego i l długości wahadła.
Zapisując to równanie jako układ dwóch równań pierwszego rzędu otrzymujemy:
![\begin{array}[]{l}\frac{dx}{dt}=y\\
\frac{dy}{dt}=-a\, x.\\
\end{array}](wyklady/nrr/mi/mi368.png) |
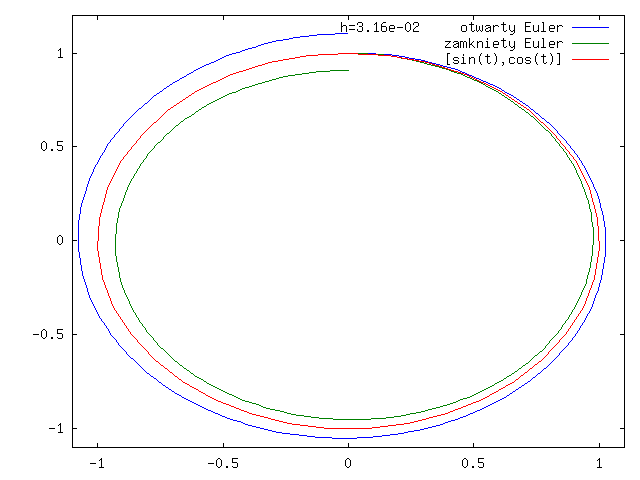
Przyjmijmy, że ![]() .
.
Znamy rozwiązania:
czyli trajektorie rozwiązania zawarte są w okręgach.
A teraz zastosujmy otwarty schemat Eulera do tego równania z warunkiem początkowym ![]() , którego rozwiązaniem jest
, którego rozwiązaniem jest ![]() z
z ![]() :
:
dla ustalonego ![]() i
i ![]() .
.
Zatem: ![]() , a
, a ![]() z
z
![]() i
i ![]()
Dla zamkniętego schematu Eulera jest analogicznie:
czy równoważnie
czyli w każdym kroku dla ustalonego ![]() musimy rozwiązać układ dwóch równań liniowych.
musimy rozwiązać układ dwóch równań liniowych.
Widać, że mimo małego kroku rzędu (![]() ) wyniki są wyraźnie gorsze niż
w przypadku skalarnym, mimo że wyjściowe równanie różniczkowe jest liniowe.
) wyniki są wyraźnie gorsze niż
w przypadku skalarnym, mimo że wyjściowe równanie różniczkowe jest liniowe.
Rozważmy wyjściowe równanie wahadła, por. Przykład 2.5.
Znów przyjmijmy, że ![]() i warunek początkowy
i warunek początkowy ![]() i
i ![]() .
Wtedy schematy Eulera przybierają odpowiednio formę:
.
Wtedy schematy Eulera przybierają odpowiednio formę:
schemat otwarty Eulera:
z ![]() i
i ![]() .
Znając
.
Znając ![]() otrzymujemy natychmiast wzór na
otrzymujemy natychmiast wzór na ![]() .
.
W przypadku schematu zamkniętego Eulera:
z ![]() i
i ![]() , musimy w każdym kroku rozwiązać układ równań nieliniowych:
, musimy w każdym kroku rozwiązać układ równań nieliniowych:
Im ![]() jest bliższe zera, tym układ jest łatwiejszy do rozwiązania.
jest bliższe zera, tym układ jest łatwiejszy do rozwiązania.
Można pokazać, że rozwiązanie wyjściowego równania ma trajektorie okresowe, co potwierdza wykres na rysunku 3.15 (tu wyliczony przy pomocy dużo dokładniejszego schematu niż schematy Eulera). W kolejnych rysunkach 3.10- 3.13 - prezentujemy przybliżone rozwiązania dla nieliniowego równania wahadła, otrzymane przy pomocy obu schematów Eulera.
3.3.1. Absolutna stabilność schematów Eulera
Rozpatrzmy ponownie modelowe zadanie skalarne, ale na długich odcinkach czasu:
Rozwiązaniem jest ![]() i wtedy
i wtedy ![]() . Im
. Im ![]() większe, tym
rozwiązanie szybciej zbiega do zera.
większe, tym
rozwiązanie szybciej zbiega do zera.
Rozpatrzmy teraz zastosowanie otwartego i zamkniętego schematu Eulera do rozwiązania tego zagadnienia. Dla otwartego schematu Eulera wiemy już, że:
Zauważmy, że przy ustalonym ![]() ciąg przybliżeń
ciąg przybliżeń ![]() jest dodatni i zbiega do zera dla
jest dodatni i zbiega do zera dla ![]() o ile zachodzi warunek:
o ile zachodzi warunek:
W przypadku gdy parametr ![]() jest ujemny i o dużym module, warunek ten wymusza to, że musimy
wziąć bardzo małe
jest ujemny i o dużym module, warunek ten wymusza to, że musimy
wziąć bardzo małe ![]() , aby otrzymać schematem otwartym Eulera rozwiązanie
przybliżone, które jest dodatnie i malejące do zera, czyli
zachowujące się jak rozwiązanie zagadnienia początkowego:
, aby otrzymać schematem otwartym Eulera rozwiązanie
przybliżone, które jest dodatnie i malejące do zera, czyli
zachowujące się jak rozwiązanie zagadnienia początkowego: ![]() .
.
Natomiast dla zamkniętego schematu Eulera widzimy, że:
Otrzymujemy wtedy, że dla dowolnego ![]() zachodzi
zachodzi
![]() i
i ![]() dla
dla ![]() , czyli nie otrzymujemy żadnego ograniczenia na krok
, czyli nie otrzymujemy żadnego ograniczenia na krok ![]() , co jest istotne, jeśli chcemy rozwiązywać równanie na długim odcinku czasu.
, co jest istotne, jeśli chcemy rozwiązywać równanie na długim odcinku czasu.
Schemat zamknięty Eulera można uznać za lepszy od schematu otwartego dla tego
zagadnienia dla ujemnego ![]() o bardzo dużym module, szczególnie na długim
odcinku czasu, ponieważ nie wymusza żadnych ograniczeń na krok
o bardzo dużym module, szczególnie na długim
odcinku czasu, ponieważ nie wymusza żadnych ograniczeń na krok ![]() . Wrócimy do
tego problemu w następnych rozdziałach.
. Wrócimy do
tego problemu w następnych rozdziałach.
3.4. Zadania
Ćwiczenie 3.1
Czy rozwiązanie ![]() zagadnienia początkowego:
zagadnienia początkowego:
jest wyznaczone jednoznacznie? Znajdź wszystkie rozwiązania ![]() tego zagadnienia początkowego.
tego zagadnienia początkowego.
Jest to równanie o zmiennych rozdzielonych (autonomiczne) ![]() z warunkiem początkowym
z warunkiem początkowym
![]() ,
więc w postaci uwikłanej
rozwiązanie ma postać
,
więc w postaci uwikłanej
rozwiązanie ma postać ![]() .
.
Ćwiczenie 3.2 (laboratoryjne)
Zaimplementuj w octavie otwarty schemat Eulera i zastosuj go do równania:
na różnych odcinkach czasu np. ![]() lub
lub ![]() i różnych wartości
i różnych wartości ![]() np.
np. ![]() .
Zmniejszając
.
Zmniejszając ![]() sprawdź, czy ten schemat znajdzie rozwiązanie różne od zera.
Następnie weź przybliżenie startowe na poziomie błędu zaokrągleń np.
sprawdź, czy ten schemat znajdzie rozwiązanie różne od zera.
Następnie weź przybliżenie startowe na poziomie błędu zaokrągleń np.
![]() i sprawdź, jakie schemat znajduje rozwiązania; w szczególności,
czy są one różne od zera.
i sprawdź, jakie schemat znajduje rozwiązania; w szczególności,
czy są one różne od zera.
Ćwiczenie 3.3
Rozpatrzmy równanie różniczkowe zwyczajne liniowe jednorodne rzędu ![]() o stałych współczynnikach:
o stałych współczynnikach:
-
Poprzez podstawienie
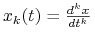
 sprowadź to równanie
do równania liniowego jednorodnego ze stałą macierzą:
sprowadź to równanie
do równania liniowego jednorodnego ze stałą macierzą:
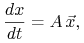
-
Znajdź wielomian charakterystyczny
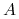 oraz dla
oraz dla 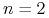 postać Jordana tej macierzy w zależności
od tego, jakie wartości własne ma
postać Jordana tej macierzy w zależności
od tego, jakie wartości własne ma 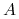 ,
, -
Przy założeniu, że
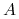 ma
ma 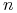 jednokrotnych wartości własnych rzeczywistych, znajdź
jednokrotnych wartości własnych rzeczywistych, znajdź
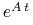 i dla
i dla 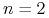 znajdź rozwiązanie zadania początkowego dla tego
równania z
warunkami początkowymi:
znajdź rozwiązanie zadania początkowego dla tego
równania z
warunkami początkowymi:
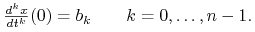
Ćwiczenie 3.4 (częściowo laboratoryjne)
Dla ![]() i macierzy
i macierzy ![]() kolejno
kolejno ![]() ,
, ![]() ,
, ![]() dla rożnych wartości parametrów
dla rożnych wartości parametrów ![]() , np.
, np. ![]() ,
naszkicuj na kartce portrety fazowe (wykresy trajektorii) równania jednorodnego:
,
naszkicuj na kartce portrety fazowe (wykresy trajektorii) równania jednorodnego:
w otoczeniu zera. Naszkicuj pole wektorowe na ekranie korzystając z funkcji octave'a
quiver() i portrety fazowe z pomocą funkcji lsode().
Ćwiczenie 3.5 (laboratoryjne)
Zaimplementuj w octavie otwarty schemat Eulera i zastosuj go do równania
![]() z
z ![]() dla różnych wartości parametru
dla różnych wartości parametru ![]() np.
np. ![]() . Narysuj na monitorze wykresy przybliżonych rozwiązań razem z wykresem rozwiązania dokładnego
. Narysuj na monitorze wykresy przybliżonych rozwiązań razem z wykresem rozwiązania dokładnego ![]() .
.
Ćwiczenie 3.6 (częściowo laboratoryjne)
Rozpatrzmy równanie ![]() . Policz wartości własne macierzy
. Policz wartości własne macierzy ![]() i porównaj z wynikiem obliczonym w octavie z użyciem odpowiedniej funkcji np.
i porównaj z wynikiem obliczonym w octavie z użyciem odpowiedniej funkcji np. eig(). Znajdź rozwiązanie ogólne tego równania.
Przy pomocy otwartego schematu Eulera i funkcji octave'a lsode() rozwiąż to równanie z ![]() na odcinku
na odcinku ![]() z
z ![]() . Porównaj wyniki rysując wykresy na ekranie obu rozwiązań i rozwiązania dokładnego, które należy też wyznaczyć.
. Porównaj wyniki rysując wykresy na ekranie obu rozwiązań i rozwiązania dokładnego, które należy też wyznaczyć.
Rozwiązanie ogólne - to ![]() , gdzie
, gdzie ![]() wektor stałych a funkcja
wektor stałych a funkcja
expm() octave'a pozwala obliczyć eksponent macierzy.
Ćwiczenie 3.7 (częściowo laboratoryjne)
Udowodnij, że przybliżenia rozwiązania układu równań ![]() z
z ![]() ,
otrzymane za pomocą otwartego (lub zamkniętego) schematu Eulera, mają normę
drugą
zbieżną do jeden, tzn.
,
otrzymane za pomocą otwartego (lub zamkniętego) schematu Eulera, mają normę
drugą
zbieżną do jeden, tzn. ![]() zbiegają do jeden, dla ustalonego czasu
zbiegają do jeden, dla ustalonego czasu ![]() z
z ![]() dążącym do zera. Zaimplementuj oba schematy Eulera dla tego równania w octave (w przypadku zamkniętego schematu Eulera
użyj operatora backslash:
dążącym do zera. Zaimplementuj oba schematy Eulera dla tego równania w octave (w przypadku zamkniętego schematu Eulera
użyj operatora backslash: \
w każdym kroku czasowym do rozwiązania odpowiedniego układu dwóch równań liniowych).
Naszkicuj na ekranie monitora portret fazowy przy pomocy plot(), lsode() i obu schematów dla różnych wartości ![]() . Policz wartości normy drugiej rozwiązań otrzymanych przy pomocy tych schematów i
. Policz wartości normy drugiej rozwiązań otrzymanych przy pomocy tych schematów i lsode() dla ustalonego czasu np. ![]() czy
czy ![]() i różnych wartości
i różnych wartości ![]() .
.
Ćwiczenie 3.8 (laboratoryjne)
Naszkicuj na ekranie monitora portrety fazowe równań liniowych ![]() dla macierzy
dla macierzy ![]() o różnych postaciach Jordana przy pomocy
o różnych postaciach Jordana przy pomocy plot(), lsode().