Zagadnienia
4. Metody dla równań różniczkowych zwyczajnych - rząd schematów
W tym rozdziale zajmiemy się pewnymi własnościami schematów dla równań różniczkowych zwyczajnych. W szczególności przedstawimy pojęcie rzędu schematu oraz zdefiniujemy, co oznacza zbieżność schematu z odpowiednim rzędem.
4.1. Kilka kolejnych schematów
Można postawić pytanie, czy istnieją schematy o wyższej dokładności niż schematy Eulera. Okazuje się, że tak jest i w tym rozdziale przedstawimy kolejne schematy, które dokładniej przybliżają rozwiązanie wyjściowego problemu różniczkowego.
Dość niska dokładność schematów Eulera, którą zaobserwowaliśmy w eksperymentach
z rozdziału 3 wynika z tego,
że pochodną rozwiązania przybliżyliśmy najprostszym ilorazem różnicowym.
W schematach Eulera przybliżamy pochodną poprzez iloraz różnicowy dla parametru ![]() i otrzymujemy:
i otrzymujemy:
| (4.1) |
o ile ![]() ma ciągłą drugą pochodną w otoczeniu
ma ciągłą drugą pochodną w otoczeniu ![]() .
.
Jeśli ![]() jest bardziej regularna, to pochodną można przybliżyć dokładniej, np.
poprzez iloraz różnicowy centralny (pochodna różnicowa centralna)
jest bardziej regularna, to pochodną można przybliżyć dokładniej, np.
poprzez iloraz różnicowy centralny (pochodna różnicowa centralna)
| (4.2) |
Dowód pozostawiamy jako zadanie.
Schemat midpoint, czyli kroku środkowego, jest
dwu-krokowy, tzn. że aby obliczyć ![]() musimy znać
musimy znać ![]() i
i ![]() , czyli
trzeba znać
, czyli
trzeba znać ![]() i
i ![]() .
.
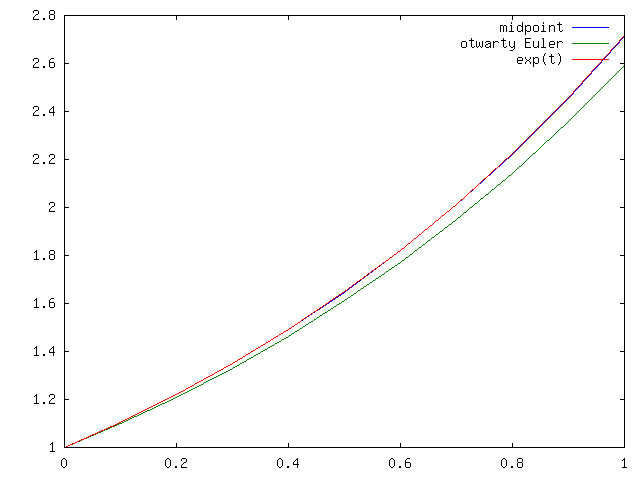
Policzmy przy pomocy tego schematu rozwiązanie zagadnienia początkowego:
Na początek weźmy ![]() i porównajmy z rozwiązaniem; za
i porównajmy z rozwiązaniem; za ![]() do naszych testów
schematu midpoint weźmiemy dokładną wartość rozwiązania:
do naszych testów
schematu midpoint weźmiemy dokładną wartość rozwiązania: ![]() , por.
rysunek 4.1.
Wyraźnie dokładniejszym okazuje się schemat midpoint.
, por.
rysunek 4.1.
Wyraźnie dokładniejszym okazuje się schemat midpoint.
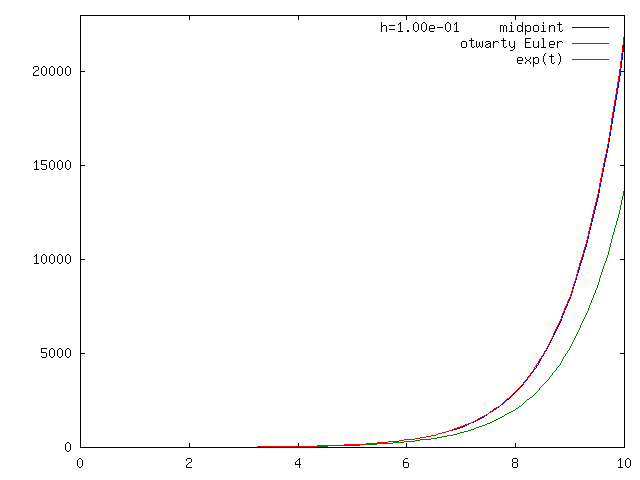
Można się zastanowić, co się stanie na dłuższym odcinku czasu, por. rysunek 4.2. Okazuje się, że schemat midpoint dokładniej działa także w tym przypadku.
Schemat ten nie jest jednak w ogóle używany. W kolejnym rozdziale wyjaśnimy dlaczego.
Inną drogą wprowadzenia nowych schematów jest skorzystanie z rozwinięcia rozwiązania w szereg Taylora: (3.6), tak jak dla schematu Eulera, ale z większą ilością członów. Otrzymujemy w ten sposób np. schemat Taylora:
Skorzystaliśmy tu z tego, że ![]() .
.
Schemat Taylora, a dokładniej schemat Taylora rzędu dwa, wygląda następująco:
| (4.4) |
gdzie ![]() i
i
![]() .
W przypadku równania autonomicznego (
.
W przypadku równania autonomicznego (![]() ) schemat się upraszcza i otrzymujemy:
) schemat się upraszcza i otrzymujemy:
Proszę zauważyć, że ogólnie ![]() jest macierzą
jest macierzą ![]() , a
, a
![]() jest wektorem wymiaru
jest wektorem wymiaru ![]() , czyli koszt schematu Taylora w
przypadku wielowymiarowym dla
, czyli koszt schematu Taylora w
przypadku wielowymiarowym dla ![]() jest dość duży.
Musimy obliczyć w każdym kroku dwa wektory tzn.
jest dość duży.
Musimy obliczyć w każdym kroku dwa wektory tzn. ![]() i
i ![]() oraz macierz
oraz macierz ![]() , wymnożyć tę macierz przez
, wymnożyć tę macierz przez ![]() i przemnożyć odpowiednie wektory przez
i przemnożyć odpowiednie wektory przez ![]() i dodać je do siebie.
Możemy w ten sposób tworzyć kolejne schematy Taylora o coraz większej dokładności - jeśli
i dodać je do siebie.
Możemy w ten sposób tworzyć kolejne schematy Taylora o coraz większej dokładności - jeśli ![]() jest funkcją dostatecznie gładką. Będą to schematy coraz droższe, szczególnie w przypadku dużego wymiaru
jest funkcją dostatecznie gładką. Będą to schematy coraz droższe, szczególnie w przypadku dużego wymiaru ![]() .
.
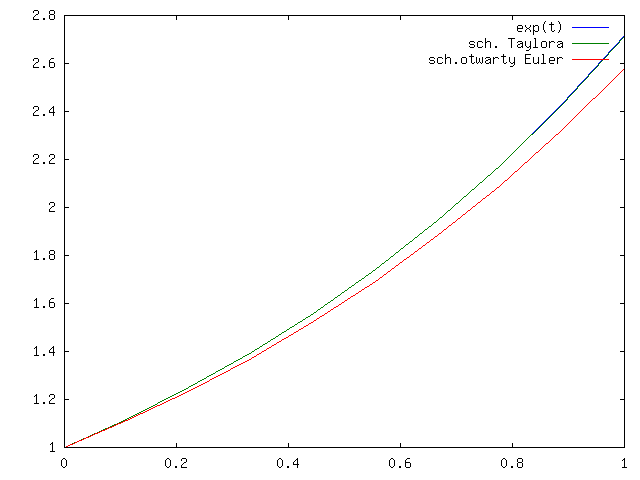
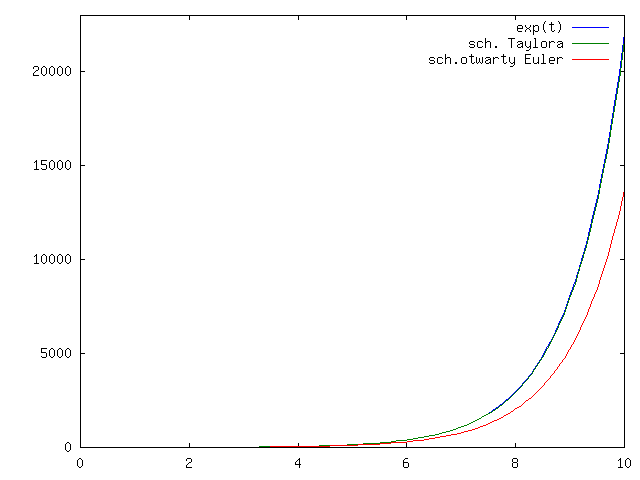
Na rysunkach 4.3 i 4.4 widać, że podobnie jak dla schematu midpoint, schemat Taylora jest dokładniejszy niż schemat Eulera otwarty.
4.1.1. Zbieżność metod - idea
Błąd schematu (ang. global error) np. Eulera otwartego, czy zamkniętego, czy schematu midpoint zastosowanych do rozwiązywania przybliżonego (3.1) możemy zdefiniować dla ustalonego ![]() jako
jako
dla ![]() ,
, ![]() rozwiązania (3.1) na
rozwiązania (3.1) na ![]() .
Zbadajmy, jak zachowuje się błąd
.
Zbadajmy, jak zachowuje się błąd ![]() wraz ze zmniejszaniem
wraz ze zmniejszaniem ![]() w ustalonym
w ustalonym
![]() . W szczególności, czy maleje do zera.
. W szczególności, czy maleje do zera.
Popatrzmy, co pokazują eksperymenty - zastosowaliśmy otwarty schemat Eulera z
różnymi krokami do policzenia przybliżenia rozwiązania równania ![]() z
z
![]() dla czasu
dla czasu ![]() , czyli znamy dokładną wartość rozwiązania
, czyli znamy dokładną wartość rozwiązania ![]() .
Ustaliliśmy
.
Ustaliliśmy ![]() , a następnie kolejno je połowiliśmy tzn.
, a następnie kolejno je połowiliśmy tzn.
![]() .
Wyniki są w tabeli 4.1.
.
Wyniki są w tabeli 4.1.
![\begin{array}[]{|c|c|c|c|}\hline h&otwarty\; Euler&midpoint&Taylor\\
\hline 5.0e-01&-4.7e-01&-7.8e-02&-7.0e-02\\
2.5e-01&-2.8e-01&-2.3e-02&-2.4e-02\\
1.2e-01&-1.5e-01&-6.4e-03&-6.6e-03\\
6.2e-02&-8.0e-02&-1.7e-03&-1.7e-03\\
3.1e-02&-4.1e-02&-4.3e-04&-4.4e-04\\
1.6e-02&-2.1e-02&-1.1e-04&-1.1e-04\\
7.8e-03&-1.1e-02&-2.7e-05&-2.8e-05\\
\hline\end{array}](wyklady/nrr/mi/mi505.png) |
Widać, że dla schematu Eulera błąd dla zmniejszonego dwukrotnie ![]() maleje dwukrotnie co sugeruje, że
błąd zachowuje się jak
maleje dwukrotnie co sugeruje, że
błąd zachowuje się jak ![]() , gdy dla schematów midpoint i schematu
Taylora błąd maleje czterokrotnie, czyli zachowuje się jak
, gdy dla schematów midpoint i schematu
Taylora błąd maleje czterokrotnie, czyli zachowuje się jak ![]() .
.
W schemacie midpoint przybliżamy pochodną różnicą centralną, dla której zachodzi:
dla dostatecznie gładkiej funkcji, a w przypadku otwartego schematu Eulera - zwykłym ilorazem różnicowym
Przy konstrukcji schematu Taylora wykorzystujemy więcej członów z rozwinięcia rozwiązania w szereg Taylora (3.6). Każdy dodatkowy człon z szeregu Taylora powinien podwyższyć dokładność danego schematu.
Dlatego też wprowadza się pojęcie rzędu lokalnego błędu schematu (ang. local
truncation error), czyli rzędu schematu.
Badamy lokalny błąd schematu względem parametru ![]() ,
jeśli wstawimy za
,
jeśli wstawimy za ![]() dokładną wartość rozwiązania
dokładną wartość rozwiązania
![]() .
Najpierw zdefiniujmy samo pojęcie schematu rozwiązywania (3.1), potem zbieżności schematu i rzędu schematu.
.
Najpierw zdefiniujmy samo pojęcie schematu rozwiązywania (3.1), potem zbieżności schematu i rzędu schematu.
Definicja 4.1
Schematem ![]() krokowym rozwiązywania zadania początkowego (3.1) ze stałym krokiem
krokowym rozwiązywania zadania początkowego (3.1) ze stałym krokiem ![]() na odcinku
na odcinku ![]() nazywamy równanie różnicowe:
nazywamy równanie różnicowe:
| (4.5) |
z warunkami startowymi ![]() dla
dla ![]() .
Jeśli
.
Jeśli ![]() nie zależy od
nie zależy od ![]() , to schemat nazywamy otwartym (ang. explicit). W przeciwnym razie - schemat nazywamy zamkniętym (ang. implicit).
, to schemat nazywamy otwartym (ang. explicit). W przeciwnym razie - schemat nazywamy zamkniętym (ang. implicit).
Schematy konstruujemy tak, aby dla ustalonego ![]() zachodziło
zachodziło
![]() .
.
Definicja 4.2
Niech ![]() rozwiązania zagadnienia początkowego (3.1).
Błąd schematu
rozwiązania zagadnienia początkowego (3.1).
Błąd schematu ![]() krokowego postaci (4.5) dla
krokowego postaci (4.5) dla ![]() definiujemy jako
definiujemy jako
a błąd globalny (ang. global error) na ![]() jako
jako
dla ![]() . Schemat jest zbieżny na
. Schemat jest zbieżny na ![]() , jeśli
, jeśli
a jest zbieżny z rzędem ![]() (ang. convergent with order
(ang. convergent with order ![]() )
(rząd błędu globalnego wynosi
)
(rząd błędu globalnego wynosi ![]() ), jeśli dodatkowo
), jeśli dodatkowo
dla pewnej stałej ![]() niezależnej od
niezależnej od ![]() (zazwyczaj zależnej
od rozwiązania
(zazwyczaj zależnej
od rozwiązania ![]() (3.1) i
(3.1) i ![]() ).
).
Definicja 4.3
Niech ![]() będzie rozwiązaniem zagadnienia
początkowego (3.1).
Dla parametru
będzie rozwiązaniem zagadnienia
początkowego (3.1).
Dla parametru ![]() i schematu
i schematu ![]() krokowego postaci (4.5) błąd lokalny (ang. local truncation error) definiujemy jako
krokowego postaci (4.5) błąd lokalny (ang. local truncation error) definiujemy jako
Definicja 4.4
Schemat (4.5) jest rzędu ![]() (ang. local truncation error is of order
(ang. local truncation error is of order ![]() ), jeśli dla
), jeśli dla ![]() rozwiązania zagadnienia początkowego (3.1) zachodzi
rozwiązania zagadnienia początkowego (3.1) zachodzi
dla pewnej dodatniej stałej ![]() niezależnej od
niezależnej od ![]() .
.
Dla otwartego schematu Eulera lokalny błąd schematu jest równy:
Z rozwinięcia w szereg Taylora widzimy, że:
o ile ![]() rozwiązanie (3.1) jest klasy
rozwiązanie (3.1) jest klasy ![]() , czyli schemat ma rząd jeden.
Analogicznie można pokazać, że rząd zamkniętego schematu Eulera jest też jeden, a rząd schematów midpoint i Taylora
wynosi dwa. Wykazanie tego, pozostawimy jako zadanie.
, czyli schemat ma rząd jeden.
Analogicznie można pokazać, że rząd zamkniętego schematu Eulera jest też jeden, a rząd schematów midpoint i Taylora
wynosi dwa. Wykazanie tego, pozostawimy jako zadanie.
4.1.2. Schematy Adamsa
Możemy też wyprowadzić schematy korzystając z równoważnej całkowej wersji zagadnienia początkowego (3.1):
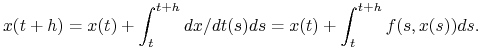 |
(4.6) |
To prowadzi do konstrukcji całej rodziny schematów (tzw. schematów
Adamsa).
Jeśli wprowadzimy siatkę równomierną z krokiem ![]() , tzn. wprowadzamy
, tzn. wprowadzamy ![]() dla
dla ![]() , to możemy przybliżyć wartość rozwiązania
, to możemy przybliżyć wartość rozwiązania ![]() zastępując w (4.6)
całką z jakiejś aproksymacji funkcji
zastępując w (4.6)
całką z jakiejś aproksymacji funkcji ![]() , którą daje się wyliczyć
znając wartości
, którą daje się wyliczyć
znając wartości ![]() dla ustalonej ilości
dla ustalonej ilości ![]() , np.
, np.
![]() . Wtedy
. Wtedy
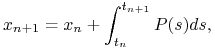 |
gdzie ![]() jest jakimś wielomianem przybliżającym
jest jakimś wielomianem przybliżającym ![]() zdefiniowanym poprzez wartości odpowiednie
zdefiniowanym poprzez wartości odpowiednie
![]() dla
dla ![]() .
.
W przypadku schematów Adamsa,
![]() definiujemy jako odpowiedni wielomian interpolacyjny Lagrange'a dla funkcji
definiujemy jako odpowiedni wielomian interpolacyjny Lagrange'a dla funkcji ![]() z węzłami w punktach
z węzłami w punktach ![]() dla
dla ![]() dla schematu zamkniętego (lub
dla schematu zamkniętego (lub
![]() dla schematu otwartego),
spełniający odpowiednie warunki interpolacyjne:
dla schematu otwartego),
spełniający odpowiednie warunki interpolacyjne:
dla ![]() kolejnych indeksów
kolejnych indeksów ![]() dla schematów Adamsa zamkniętych i
dla schematów Adamsa zamkniętych i ![]() dla schematów Adamsa otwartych.
Wtedy
otrzymujemy klasę zamkniętych schematów Adamsa-Moultona postaci:
dla schematów Adamsa otwartych.
Wtedy
otrzymujemy klasę zamkniętych schematów Adamsa-Moultona postaci:
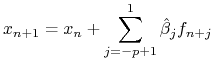 |
lub otwartych schematów Adamsa-Bashfortha:
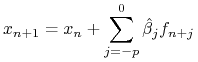 |
Przenumerowując indeksy uzyskujemy schemat zamknięty Adamsa-Moultona ![]() krokowy:
krokowy:
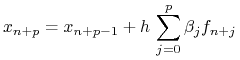 |
lub otwarty ![]() krokowy Adamsa-Bashfortha:
krokowy Adamsa-Bashfortha:
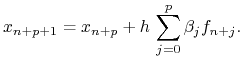 |
Oczywiście w obu przypadkach ![]() nie zależą od rozwiązania
nie zależą od rozwiązania ![]() , ani od
, ani od ![]() .
.
W szczególności dla ![]() ,
, ![]() jest wielomianem interpolacyjnym stałym,
zdefiniowanym przez wartość w jednym punkcie odpowiednio
jest wielomianem interpolacyjnym stałym,
zdefiniowanym przez wartość w jednym punkcie odpowiednio ![]() czy
czy ![]() . Dla
. Dla
otrzymujemy schemat otwarty Eulera:
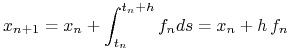 |
Biorąc wartość
w punkcie ![]() uzyskujemy schemat zamknięty Eulera.
A dla
uzyskujemy schemat zamknięty Eulera.
A dla ![]() ,
,
![]() jest wielomianem liniowym interpolującym
jest wielomianem liniowym interpolującym ![]() w punktach
w punktach ![]() i
i ![]() . Wtedy otrzymujemy
schemat trapezów (ang. trapezoidal scheme):
. Wtedy otrzymujemy
schemat trapezów (ang. trapezoidal scheme):
czyli
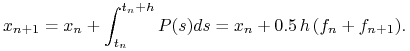 |
(4.7) |
Można pokazać, że schemat trapezów jest rzędu dwa.
W przypadku, gdy punkt ![]() czyli
czyli ![]() nie jest uwzględniony w definicji
nie jest uwzględniony w definicji ![]() tzn.
tzn. ![]() rozpatrujemy otwarte schematy Adamsa, które też
nazywamy schematami Adamsa-Bashforda,
np. schemat otwarty Eulera.
W przeciwnym przypadku otrzymujemy schematy zamknięte,
które nazywamy schematami Adamsa-Moultona: np. schemat zamknięty Eulera
lub schemat trapezów.
rozpatrujemy otwarte schematy Adamsa, które też
nazywamy schematami Adamsa-Bashforda,
np. schemat otwarty Eulera.
W przeciwnym przypadku otrzymujemy schematy zamknięte,
które nazywamy schematami Adamsa-Moultona: np. schemat zamknięty Eulera
lub schemat trapezów.
4.2. Schematy liniowe wielokrokowe
Definicja 4.5
Dla zadania początkowego (3.1)
schematem liniowym wielokrokowym (ang. linear multistep) - dokładniej ![]() krokowym dla stałego kroku dla
krokowym dla stałego kroku dla ![]() nazywamy równanie różnicowe:
nazywamy równanie różnicowe:
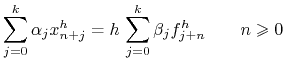 |
(4.8) |
z ![]() i
i ![]() dla
dla ![]() .
.
Jeśli ![]() ,
to schemat nazywamy zamkniętym, a w przeciwnym wypadku mówimy o schemacie otwartym.
,
to schemat nazywamy zamkniętym, a w przeciwnym wypadku mówimy o schemacie otwartym.
Jeśli znamy
![]() to możemy wyliczyć rozwiązanie schematu
to możemy wyliczyć rozwiązanie schematu ![]() dla
dla ![]() i
i ![]() (o ile ono istnieje, co w przypadku schematów zamkniętych nie jest oczywiste).
(o ile ono istnieje, co w przypadku schematów zamkniętych nie jest oczywiste).
Zgodnie z Definicją 4.4
schemat liniowy ![]() -krokowy ma rząd
-krokowy ma rząd ![]() jeśli dla
jeśli dla ![]() rozwiązania zagadnienia (3.1) dla
rozwiązania zagadnienia (3.1) dla
![]() takich, że
takich, że ![]() lokalny błąd schematu spełnia
lokalny błąd schematu spełnia
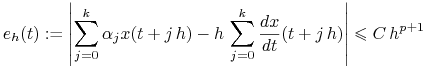 |
(4.9) |
ze stałą niezależną od ![]() ,
czyli
,
czyli ![]() .
.
Jeśli za ![]() weźmiemy wartości rozwiązania w punktach czasu
weźmiemy wartości rozwiązania w punktach czasu ![]() ,
to błąd schematu wynosi
,
to błąd schematu wynosi ![]() (dla gładkiego rozwiązania).
(dla gładkiego rozwiązania).
Oczywiście schematy Adamsa opisane w rozdziale 4.1.2 są szczególnym przypadkiem schematów liniowych wielokrokowych. Tak więc schematy: otwarty i zamknięty Eulera, schemat midpoint, lub schemat trapezów są schematami wielokrokowymi liniowymi - w myśl naszej definicji.
4.3. Schematy jednokrokowe
W tym podrozdziale wprowadzimy pojęcie schematu jednokrokowego:
Definicja 4.6
Dla zadania początkowego (3.1)
schematem jednokrokowym dla stałego kroku ![]() nazywamy równanie różnicowe:
nazywamy równanie różnicowe:
| (4.10) |
gdzie ![]() a
a ![]() jest funkcją ciągłą określoną na
jest funkcją ciągłą określoną na ![]() dla
dla ![]() otoczenia
otoczenia ![]() .
Dodatkowo, jeśli
.
Dodatkowo, jeśli ![]() nie zależy od
nie zależy od
![]() , to schemat jednokrokowy nazywamy otwartym, a w przeciwnym wypadku mówimy o schemacie zamkniętym.
, to schemat jednokrokowy nazywamy otwartym, a w przeciwnym wypadku mówimy o schemacie zamkniętym.
W przypadku schematów otwartych możemy wyliczyć ![]() znając
znając ![]() , natomiast w przypadku schematów zamkniętych
musimy rozwiązać liniowy, bądź nieliniowy układ równań.
Do tej pory poznaliśmy dwa schematy jednokrokowe (które zarazem są schematami liniowymi wielokrokowymi) - czyli oba schematy Eulera i schemat trapezów.
, natomiast w przypadku schematów zamkniętych
musimy rozwiązać liniowy, bądź nieliniowy układ równań.
Do tej pory poznaliśmy dwa schematy jednokrokowe (które zarazem są schematami liniowymi wielokrokowymi) - czyli oba schematy Eulera i schemat trapezów.
Analogicznie do przypadku schematów liniowych wielokrokowych, zgodnie z Definicją 4.4,
schemat jednokrokowy ma rząd ![]() , jeśli dla
, jeśli dla ![]() rozwiązania zagadnienia (3.1) dla
rozwiązania zagadnienia (3.1) dla ![]() ,
, ![]() i
i
![]() lokalny błąd schematu spełnia:
lokalny błąd schematu spełnia:
ze stałą ![]() niezależną od
niezależną od ![]() , czyli
, czyli ![]() dla dostatecznie gładkiego rozwiązania.
dla dostatecznie gładkiego rozwiązania.
4.3.1. Schematy Rungego-Kutty
Podstawową klasą schematów jednokrokowych są tzw. schematy Rungego-Kutty lub - mówiąc krótko - schematy Rungego. Idea ich jest prosta.
Załóżmy, że znamy ![]() , i chcemy wyliczyć wartość
, i chcemy wyliczyć wartość ![]() ze wzoru uwzględniającego wartość pola wektorowego nie tylko w
ze wzoru uwzględniającego wartość pola wektorowego nie tylko w ![]() , ale również w
dodatkowym punkcie
, ale również w
dodatkowym punkcie
![]() .
Wtedy
.
Wtedy
Biorąc schemat otwarty Eulera z krokiem ![]() otrzymujemy punkt
otrzymujemy punkt
który, jak wiemy, przybliża ![]() , ale niedokładnie.
Możemy policzyć wartość pola wektorowego
, ale niedokładnie.
Możemy policzyć wartość pola wektorowego ![]() w tym punkcie i następnie, wykorzystując wartość
w tym punkcie i następnie, wykorzystując wartość
![]() i
i ![]() , znaleźć lepsze
przybliżenie
, znaleźć lepsze
przybliżenie ![]() - czyli np. za przybliżenie pola wektorowego wziąć
ważoną średnią obu wartości
- czyli np. za przybliżenie pola wektorowego wziąć
ważoną średnią obu wartości ![]() dla pewnych ustalonych wag
dla pewnych ustalonych wag
![]() .
Możliwości jest wiele. Pojawia się pytanie:
jak oceniać różne konstrukcje
.
Możliwości jest wiele. Pojawia się pytanie:
jak oceniać różne konstrukcje ![]() ?
Można tak dobierać
?
Można tak dobierać ![]() , aby rząd schematu był możliwie duży.
, aby rząd schematu był możliwie duży.
Załóżmy, że ![]() . Wtedy
szukamy schematu postaci:
. Wtedy
szukamy schematu postaci:
| (4.11) |
tak, aby schemat miał maksymalny rząd.
Rozwijamy rozwiązanie ![]() w szereg Taylora:
w szereg Taylora:
i rozwijając ostatni z członów (4.11) w punkcie ![]() otrzymujemy:
otrzymujemy:
Skorzystaliśmy z tego, że ![]() .
Zatem, wstawiając dwa ostatnie równania do (4.11) otrzymujemy
warunki na to,
aby schemat był rzędu dwa:
.
Zatem, wstawiając dwa ostatnie równania do (4.11) otrzymujemy
warunki na to,
aby schemat był rzędu dwa:
Tak więc otrzymaliśmy całą rodzinę schematów Rungego-Kutty rzędu dwa, np.:
-
Zmodyfikowany schemat Eulera
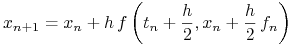
(4.12) dla
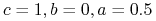 ,
, -
Schemat Heuna
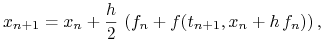
(4.13) dla
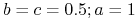 .
.
Warto zauważyć, że w niektórych publikacjach wszystkie schematy otwarte Rungego-Kutty rzędu dwa nazywane są zmodyfikowanym schematem Eulera.
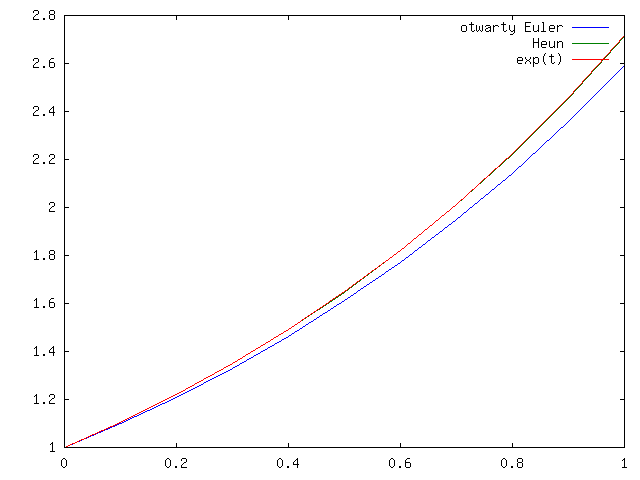
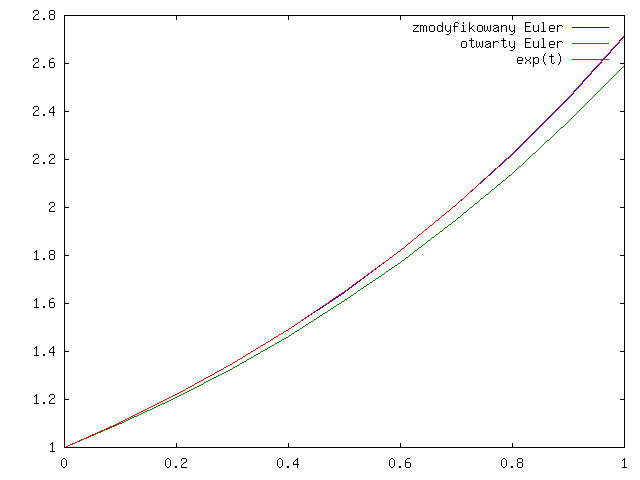
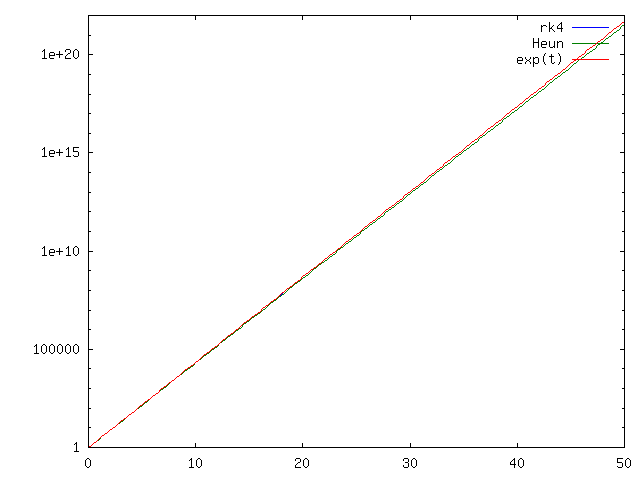
Na rysunkach 4.6 i 4.5 pokazano rozwiązania uzyskane tymi dwoma schematami dla zadania ![]() z
z ![]() na
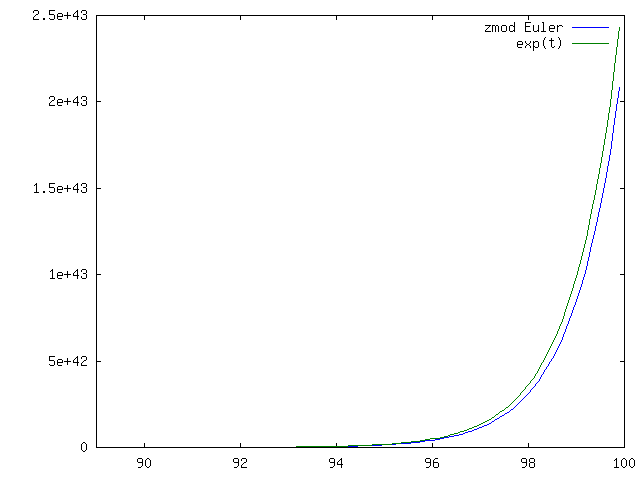
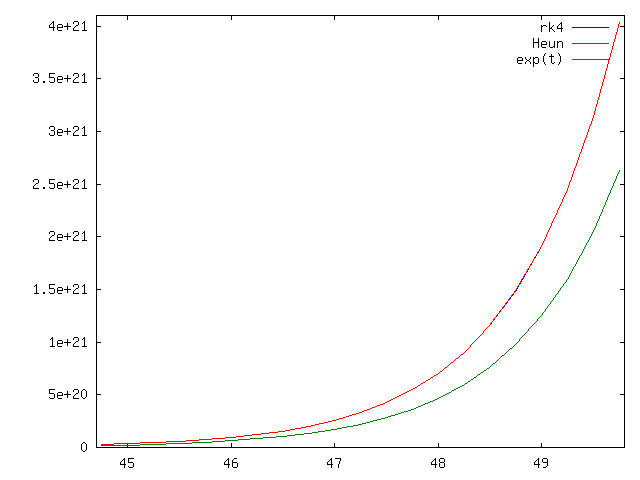
na ![]() . Widać, że wykresy się pokrywają z wykresem rozwiązania. W porównaniu do otwartego schematu Eulera widzimy znaczącą poprawę. Zobaczmy, co się dzieje na dłuższym odcinku czasu w przypadku schematu Heuna, por.
rysunek 4.7.
. Widać, że wykresy się pokrywają z wykresem rozwiązania. W porównaniu do otwartego schematu Eulera widzimy znaczącą poprawę. Zobaczmy, co się dzieje na dłuższym odcinku czasu w przypadku schematu Heuna, por.
rysunek 4.7.
4.3.1.1. Graficzne wytłumaczenie zmodyfikowanego schematu Eulera
Na rysunku 4.8 zawarliśmy graficzne wytłumaczenie jednego kroku zmodyfikowanego schematu Eulera.
Punkt ![]() - oznacza
- oznacza ![]() , czyli wcześniej obliczone przybliżenie dla czasu
, czyli wcześniej obliczone przybliżenie dla czasu ![]() .
Chcemy wyznaczyć
przybliżenie dla czasu
.
Chcemy wyznaczyć
przybliżenie dla czasu ![]() .
Otwarty schemat Eulera w jednym kroku przyjmuje za różnicę między kolejnymi
punktami
.
Otwarty schemat Eulera w jednym kroku przyjmuje za różnicę między kolejnymi
punktami
![]() , czyli idzie w kierunku pola wektorowego
w punkcie
, czyli idzie w kierunku pola wektorowego
w punkcie ![]() , czyli na naszym rysunku daje to punkt
, czyli na naszym rysunku daje to punkt
![]() . Z kolei w zmodyfikowanym schemacie Eulera przyjmujemy za
różnicę
. Z kolei w zmodyfikowanym schemacie Eulera przyjmujemy za
różnicę ![]() pomnożone przez kierunek pola wyznaczonego w dodatkowym
pomocniczym
punkcie
pomnożone przez kierunek pola wyznaczonego w dodatkowym
pomocniczym
punkcie ![]() oznaczonym jako
oznaczonym jako ![]() , tzn.
idziemy w kierunku
, tzn.
idziemy w kierunku ![]() i otrzymujemy w efekcie punkt
i otrzymujemy w efekcie punkt ![]() .
.
Na rysunku widać, że jeśli nachylenie pola wektorowego
mocno się zmienia, to pole w punkcie ![]() powinno mieć lepszy kierunek
niż w
powinno mieć lepszy kierunek
niż w ![]() , czy w
, czy w ![]() .
Jest to oczywiście argument heurystyczny.
.
Jest to oczywiście argument heurystyczny.
Analogicznie konstruuje się schematy Rungego wyższych rzędów
poprzez wprowadzenie większej ilości kroków pośrednich, jak również schematy
zamknięte Rungego -
dopuszczając wartość ![]() w schemacie.
w schemacie.
Podamy kilka wzorów na powszechnie używany otwarty schemat Rungego-Kutty czwartego rzędu.
Najpierw definiujemy cztery wartości:
![\begin{array}[]{l}K_{1}=f(t_{n},x_{n})\\
K_{2}=f(t_{n}+\frac{h}{2},x_{n}+\frac{h}{2}\, K_{1})\\
K_{3}=f(t_{n}+\frac{h}{2},x_{n}+\frac{h}{2}\, K_{2})\\
K_{4}=f(t_{n}+h,x_{n}+h\, K_{3})\end{array}](wyklady/nrr/mi/mi544.png) |
(4.14) |
i otrzymujemy ostateczny wzór:
| (4.15) |
schematu rzędu cztery (co oczywiście wymaga dowodu).
Istnieje oczywiście cała rodzina otwartych schematów Rungego-Kutty rzędu cztery. Tu podaliśmy tylko przykładowy schemat z tej rodziny.
Popatrzmy jak działa ten schemat w porównaniu ze schematem Heuna dla naszego modelowego zagadnienia
![]() z
z ![]() .
.
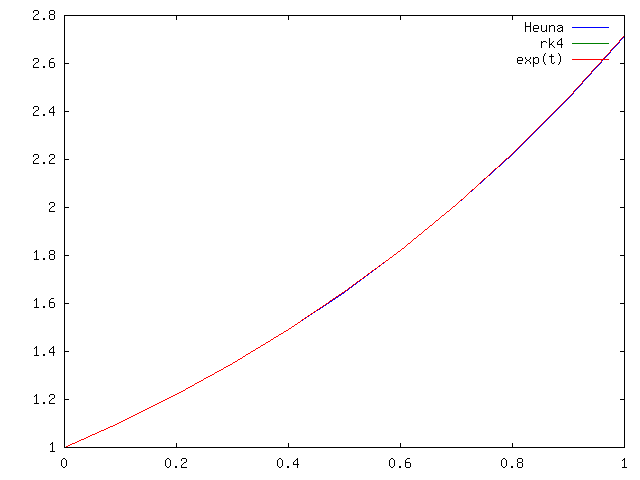
Na odcinku ![]() dla
dla ![]() oba schematy praktycznie pokrywają się z rozwiązaniem, por. rysunek 4.9.
oba schematy praktycznie pokrywają się z rozwiązaniem, por. rysunek 4.9.
4.4. Zadania
Rozwiń funkcje w szereg Taylora.
Ćwiczenie 4.2
Pokaż, że rząd schematów Eulera wynosi jeden, o ile rozwiązanie zadania Cauchy'ego jest klasy ![]() .
.
Ćwiczenie 4.3
Pokaż, że rząd schematu kroku środkowego wynosi ![]() , o ile rozwiązanie zadania Cauchy'ego jest klasy
, o ile rozwiązanie zadania Cauchy'ego jest klasy ![]() dla
dla ![]() .
.
Ćwiczenie 4.4
Znajdź rząd schematu Taylora (4.4) dla rozwiązania dostatecznie gładkiego.
Ćwiczenie 4.5
Znajdź wzór na schemat Taylora rzędu trzy.
Ćwiczenie 4.6
Rozpatrzmy rodzinę schematów:
Określ rząd schematu w zależności od wartości parametrów ![]() . Dla jakich
. Dla jakich ![]() rząd jest największy? Dla jakich wartości parametrów schemat będzie zamknięty, a dla jakich otwarty?
rząd jest największy? Dla jakich wartości parametrów schemat będzie zamknięty, a dla jakich otwarty?
Ćwiczenie 4.7
Wyprowadź otwarty dwukrokowy schemat Adamsa bazujący na wielomianie
interpolacyjnym stopnia jeden (żeby policzyć
![]() potrzebujemy
potrzebujemy ![]() ,
,
![]() i
i ![]() , tak jak opisano w rozdziale 4.1.2). Zbadaj rząd
schematu.
, tak jak opisano w rozdziale 4.1.2). Zbadaj rząd
schematu.
Zgodnie z zasadą konstrukcji schematów Adamsa musimy scałkować na odcinku ![]() wielomian liniowy interpolacyjny
wielomian liniowy interpolacyjny ![]() . Otrzymujemy schemat
. Otrzymujemy schemat ![]() .
.
Ćwiczenie 4.8
Wyprowadź otwarty trzykrokowy schemat Adamsa bazujący na wielomianie interpolacyjnym stopnia dwa (żeby policzyć
![]() potrzebujemy
potrzebujemy ![]() i
i
![]() , tak jak opisano w rozdziale 4.1.2). Zbadaj rząd schematu.
, tak jak opisano w rozdziale 4.1.2). Zbadaj rząd schematu.
Ćwiczenie 4.9
Wyprowadź zamknięty dwukrokowy schemat Adamsa bazujący na wielomianie interpolacyjnym stopnia dwa (żeby policzyć ![]() potrzebujemy
potrzebujemy ![]() i
i ![]() , tak jak opisano w rozdziale 4.1.2). Zbadaj rząd schematu.
, tak jak opisano w rozdziale 4.1.2). Zbadaj rząd schematu.
Ćwiczenie 4.10 (średnio trudne)
Rozpatrzmy rodzinę schematów:
Określ rząd schematu w zależności od wartości parametrów ![]() . Dla jakich wartości rząd jest największy? Dla jakich wartości parametrów schemat będzie zamknięty, a dla jakich otwarty?
. Dla jakich wartości rząd jest największy? Dla jakich wartości parametrów schemat będzie zamknięty, a dla jakich otwarty?
Ćwiczenie 4.11 (trudne)
Udowodnij, że schemat (4.15) ma rząd cztery.
Ćwiczenie 4.12 (laboratoryjne)
Zbadaj eksperymentalnie metodą połowienia kroków rząd lokalnego błędu schematu dla schematów:
-
otwartego schematu Eulera (3.4),
-
zamkniętego schematu Eulera (3.5),
-
schematu midpoint (4.3),
-
schematu Taylora (4.4),
-
schematu Heuna (4.13),
-
schematu trapezów (4.7),
-
zmodyfikowanego schematu Eulera (4.12),
-
schematu Rungego rzędu cztery (4.15).
zastosowanych do modelowego zadania ![]() z
z ![]() z rozwiązaniem
z rozwiązaniem ![]() .
Tzn. dla ustalonego
.
Tzn. dla ustalonego ![]() , np.
, np. ![]() i kolejnych połowionych kroków
i kolejnych połowionych kroków ![]() z
z ![]() liczymy
lokalny błąd schematu
liczymy
lokalny błąd schematu ![]() , por. (4.9), i następnie stosunek
, por. (4.9), i następnie stosunek ![]() .
Jeśliby ten stosunek wynosił w przybliżeniu
.
Jeśliby ten stosunek wynosił w przybliżeniu ![]() , to lokalny błąd schematu zachowuje się jak
, to lokalny błąd schematu zachowuje się jak ![]() , oznacza to, że schemat posiada rząd
, oznacza to, że schemat posiada rząd ![]() przynajmniej dla tego zadania początkowego.
przynajmniej dla tego zadania początkowego.