Zagadnienia
5. Metody dla równań różniczkowych zwyczajnych - teoria zbieżności
W tym rozdziale przedstawimy teorię zbieżności schematów jednokrokowych i wielokrokowych.
Rozpatrzymy tylko przypadek skalarny, ale teoria dla układów równań jest analogiczna. Wystarczy tylko moduł zastąpić przez jakąś normę w ![]() np. normę euklidesową.
np. normę euklidesową.
5.1. Teoria zbieżności schematów jednokrokowych
Teoria zbieżności schematów jednokrokowych jest teorią odrębną od teorii dla schematów wielokrokowych liniowych.
Okaże się, że kluczowym pojęciem jest tu zgodność schematu jednokrokowego - inaczej konsystentność, którą definiujemy następująco:
Definicja 5.1
Schemat jednokrokowy (4.10) jest zgodny (konsystentny), (ang. consistent) jeśli:
-
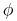 jest ciągłą ze względu na wszystkie zmienne
jest ciągłą ze względu na wszystkie zmienne -
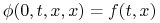 dla wszystkich
dla wszystkich 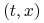 .
. -
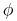 jest lipschitzowska ze względu na zmienne
jest lipschitzowska ze względu na zmienne 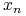 i
i 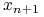 tzn. istnieje
tzn. istnieje 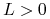 takie, że dla wszystkich
takie, że dla wszystkich 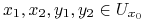
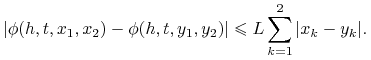
Twierdzenie 5.1 (o zbieżności schematów jednokrokowych)
Jeśli rozwiązanie zagadnienia początkowego (3.1) ![]() , schemat jednokrokowy jest zgodny i jest rzędu
, schemat jednokrokowy jest zgodny i jest rzędu ![]() , to
ten schemat jest zbieżny z rzędem
, to
ten schemat jest zbieżny z rzędem ![]() .
.
Dowód zostanie tutaj przedstawiony
dla prostoty tylko dla schematów otwartych z rzędem ![]() tj.
tj. ![]() .
Dowód w całej ogólności można znaleźć np. w [23].
.
Dowód w całej ogólności można znaleźć np. w [23].
Oznaczmy przez ![]() , czyli błąd pomiędzy obliczonym schematem przybliżeniem
rozwiązania dla czasu
, czyli błąd pomiędzy obliczonym schematem przybliżeniem
rozwiązania dla czasu ![]() , a dokładną wartością rozwiązania
, a dokładną wartością rozwiązania ![]() . Niech
. Niech
![]() ,
czyli
,
czyli ![]() to lokalny błąd schematu dla czasu
to lokalny błąd schematu dla czasu ![]() .
Wtedy otrzymujemy, że
.
Wtedy otrzymujemy, że
a stąd, korzystając ze zgodności schematu, a dokładniej lipschitzowskości funkcji ![]() ,
por. Definicja 5.1, otrzymujemy
,
por. Definicja 5.1, otrzymujemy
Dalej, poprzez indukcję matematyczną otrzymujemy:
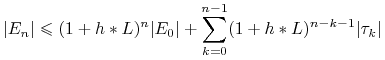 |
Korzystając z tego, że (![]() )
)
dla ![]() takich, że
takich, że ![]() widzimy, że
widzimy, że
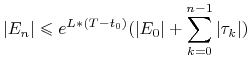 |
Zauważmy, że ![]() . Widzimy też, że
. Widzimy też, że
Ponieważ schemat ma rząd ![]() i
i ![]() , to
, to ![]() zatem
zatem
W szczególności zbieżność z rzędem ![]() oznacza dla ustalonego
oznacza dla ustalonego ![]() i
i
![]() , że
, że
Przykład 5.1
Zgodność otwartego schematu Eulera.
W zasadzie sprawdzenie konsystentności (zgodności) schematu jest w tym przypadku oczywiste,
ponieważ funkcja ![]() , czyli spełnia założenia zgodności.
Dodatkowo wiemy, że schemat ma rząd jeden, więc jeśli
, czyli spełnia założenia zgodności.
Dodatkowo wiemy, że schemat ma rząd jeden, więc jeśli ![]() rozwiązanie zadania początkowego (3.1) należy do
rozwiązanie zadania początkowego (3.1) należy do ![]() , to
, to ![]() dla
dla ![]() , co potwierdzają wyniki eksperymentów z tabeli 4.1 w przypadku skalarnym dla równania
, co potwierdzają wyniki eksperymentów z tabeli 4.1 w przypadku skalarnym dla równania ![]() z
z ![]() .
.
5.2. Teoria zbieżności schematów liniowych wielokrokowych
Teoria zbieżności dla schematów wielokrokowych liniowych różni się od teorii zbieżności dla schematów jednokrokowych. Precyzyjniej pisząc - używamy tak samo jak w przypadku schematów jednokrokowych pojęcie rzędu schematu, ale równie ważne jest pojęcie stabilności schematu. Używając nieformalnego języka - stabilność schematu oznacza to, że błędy z poprzednich kroków się nie kumulują, a wręcz zanikają.
5.2.1. Stabilność, zgodność
Na początku rozważmy dowolny schemat liniowy wielokrokowy (4.8) zastosowany do równania z polem wektorowym równym zero tzn. do zagadnienia początkowego:
którego jedynym rozwiązaniem jest rozwiązania stałe ![]() .
Nasz schemat staje się wtedy
równaniem różnicowym liniowym jednorodnym o stałych współczynnikach:
.
Nasz schemat staje się wtedy
równaniem różnicowym liniowym jednorodnym o stałych współczynnikach:
| (5.1) |
Wprowadzając wielomian
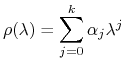 |
(5.2) |
otrzymujemy, że jeśli ![]() jest zerem (pierwiastkiem) wielomianu
jest zerem (pierwiastkiem) wielomianu ![]() , to
ciąg
, to
ciąg
jest rozwiązaniem równania różnicowego. Jeśli zero jest dwukrotne , to otrzymujemy nowe rozwiązanie związane z tym pierwiastkiem tzn.:
i tak dalej - jeśli zero jest trzykrotne, to kolejne rozwiązanie:
W każdym razie - co ważne - jeśli jakiś pierwiastek ![]() ma moduł
ma moduł ![]() lub
lub ![]() , ale krotność pierwiastka jest większa od jeden, to istnieją rozwiązania nieograniczone, a dokładnie, zachodzi dla pewnych rozwiązań:
, ale krotność pierwiastka jest większa od jeden, to istnieją rozwiązania nieograniczone, a dokładnie, zachodzi dla pewnych rozwiązań:
Jeśli pierwiastek ![]() to zawsze wszystkie rozwiązania z nim związane spełniają
to zawsze wszystkie rozwiązania z nim związane spełniają
Podsumowując: jeśli jakiś pierwiastek ma moduł mniejszy od jeden, albo ma moduł jeden i krotność jeden, to rozwiązania z nim związane są ograniczone. Wydaje się, że wymaganie żeby wszystkie rozwiązania schematu zastosowanego do równania z prawą stroną równą zero były ograniczone jest jak najbardziej uzasadnione.
Dlatego w ten sposób definiujemy stabilność (ang. stability) schematu liniowego wielokrokowego (4.8):
Definicja 5.2
Schemat (4.8) jest stabilny, jeśli każdy pierwiastek ![]() wielomianu
wielomianu
![]() spełnia
spełnia
a w przypadku jeśli ![]() , to krotność pierwiastka
, to krotność pierwiastka ![]() wynosi jeden.
wynosi jeden.
Dodatkowo wprowadzamy pojęcie silnej stabilności schematu (ang. strong stability):
Definicja 5.3
Schemat (4.8) jest silnie stabilny, jeśli spełnia Definicję 5.2 stabilności, i
jeśli ![]() jest zerem wielomianu
jest zerem wielomianu
![]() takim, że
takim, że
![]() to
to ![]() .
.
Pojęcie silnej stabilności nie wpływa na samą teorię zbieżności schematów, ale można się spodziewać, że schematy silnie stabilne zachowują się lepiej, por. rozdział 5.2.2.
W praktycznych obliczeniach wszystkie używane schematy liniowe wielokrokowe są silnie stabilne.
5.2.1.1. Zgodność schematu
Możemy oczekiwać, że jednym z rozwiązań naszego równania różnicowego (5.1) będzie rozwiązanie stałe:
![]() , czyli oczekujemy żeby
, czyli oczekujemy żeby ![]() było pierwiastkiem wielomianu
było pierwiastkiem wielomianu ![]() , tzn.
, tzn. ![]() . Ten warunek nazwiemy prezgodnością (ang. preconsistency) schematu.
. Ten warunek nazwiemy prezgodnością (ang. preconsistency) schematu.
Dodatkowo rozpatrzmy drugie proste równanie z warunkiem początkowym:
którego rozwiązaniem jest ![]() .
Jeśli zastosujemy schemat do tego równania (zawsze
.
Jeśli zastosujemy schemat do tego równania (zawsze ![]() ), to otrzymujemy następujące liniowe równanie różnicowe o stałych współczynnikach:
), to otrzymujemy następujące liniowe równanie różnicowe o stałych współczynnikach:
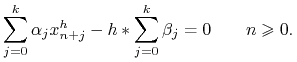 |
Dodatkowo wprowadzimy wielomian:
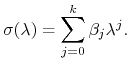 |
Zakładając, że schemat jest dokładny w ![]() dla tego zagadnienia początkowego tzn.
wstawiając
dla tego zagadnienia początkowego tzn.
wstawiając ![]() otrzymujemy:
otrzymujemy:
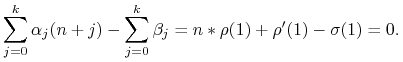 |
Jeśli założymy, że schemat jest prezgodny, to powyższe równanie daje nam:
| (5.3) |
Wprowadzamy pojęcie zgodności (konsystentności) schematu liniowego wielokrokowego:
Definicja 5.4
Schemat liniowy wielokrokowy (4.8) jest zgodny (konsystentny), (ang.consistent) jeśli zachodzi (5.3).
Nie jest trudno pokazać, że ten warunek jest równoważny temu, że rząd schematu jest co najmniej jeden, tzn. prawdziwe jest następujące stwierdzenie:
Stwierdzenie 5.1
Schemat liniowy wielokrokowy (4.8) jest zgodny wtedy i tylko wtedy, gdy rząd schematu wynosi co najmniej jeden.
Dowód pozostawiamy jako zadanie, por. ćwiczenie 5.14.
5.2.1.2. Zbieżność
Twierdzenie 5.2 (o zbieżności schematów wielokrokowych)
Jeśli rozwiązanie zagadnienia początkowego ![]() , schemat liniowy
, schemat liniowy ![]() -krokowy jest rzędu
-krokowy jest rzędu ![]() dla
dla ![]() i jest stabilny, oraz wartości startowe
i jest stabilny, oraz wartości startowe ![]() dla
dla ![]() spełniają nierówność:
spełniają nierówność:
dla pewnej stałej nieujemnej ![]() niezależnej od
niezależnej od ![]() ,
to ten
schemat jest zbieżny z rzędem
,
to ten
schemat jest zbieżny z rzędem ![]() .
.
Przykład 5.2
Zbieżność otwartego schematu Eulera jako schematu liniowego wielokrokowego.
Wiemy już, że rząd otwartego schematu Eulera wynosi jeden. Wystarczy więc zbadać stabilność schematu.
Wielomian ![]() zatem ma jeden pierwiastek
zatem ma jeden pierwiastek ![]() więc schemat jest stabilny, a nawet silnie stabilny.
Jeśli rozwiązanie jest klasy
więc schemat jest stabilny, a nawet silnie stabilny.
Jeśli rozwiązanie jest klasy ![]() , to zbieżność zachodzi z rzędem jeden, co potwierdzają wyniki eksperymentów z tabeli 4.1 w przypadku skalarnym dla równania
, to zbieżność zachodzi z rzędem jeden, co potwierdzają wyniki eksperymentów z tabeli 4.1 w przypadku skalarnym dla równania ![]() z
z ![]() .
.
5.2.2. Stabilność, a silna stabilność
Rozpatrzmy schemat kroku środkowego (4.3), który jest dwukrokowym schematem liniowym rzędu dwa (zadanie). Nietrudno sprawdzić, że jest to schemat stabilny, ale nie silnie stabilny.
Rozpatrzmy nasze modelowe równanie liniowe:
którego rozwiązanie ![]() jest równe
jest równe ![]() . Zastosujmy schemat midpoint biorąc za
. Zastosujmy schemat midpoint biorąc za ![]() dokładną wartość rozwiązania
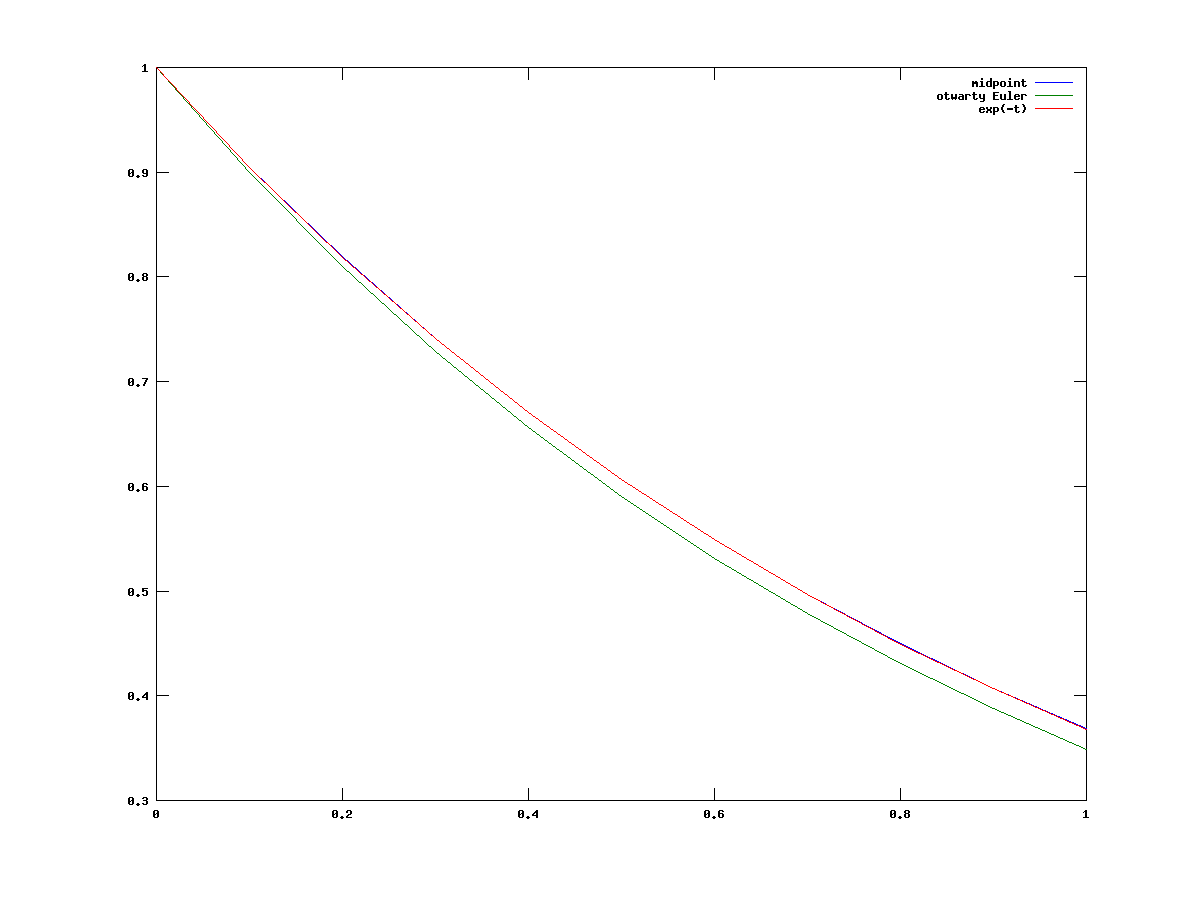
dokładną wartość rozwiązania ![]() . Narysujmy wykres rozwiązania przybliżonego otrzymanego tym schematem i schematem Eulera otwartym dla
. Narysujmy wykres rozwiązania przybliżonego otrzymanego tym schematem i schematem Eulera otwartym dla ![]() na odcinku
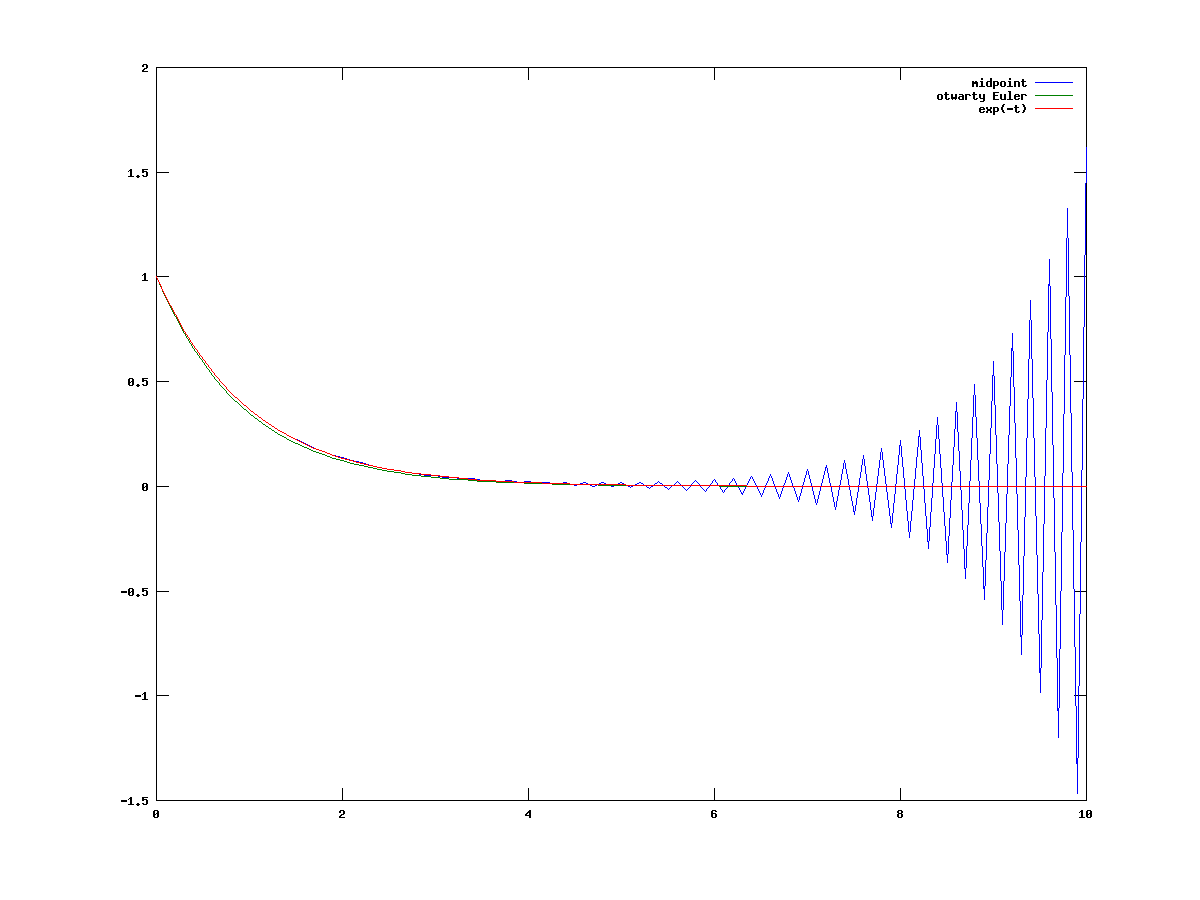
na odcinku ![]() , por. rysunek 5.1, i potem na
, por. rysunek 5.1, i potem na ![]() , por. rysunek 5.2.
W tym drugim przypadku rozwiązanie przybliżone otrzymane schematem midpoint od pewnego momentu przestaje zachowywać się jak rozwiązanie dokładne
, por. rysunek 5.2.
W tym drugim przypadku rozwiązanie przybliżone otrzymane schematem midpoint od pewnego momentu przestaje zachowywać się jak rozwiązanie dokładne ![]() , tzn. widzimy coraz większe oscylacje.
, tzn. widzimy coraz większe oscylacje.
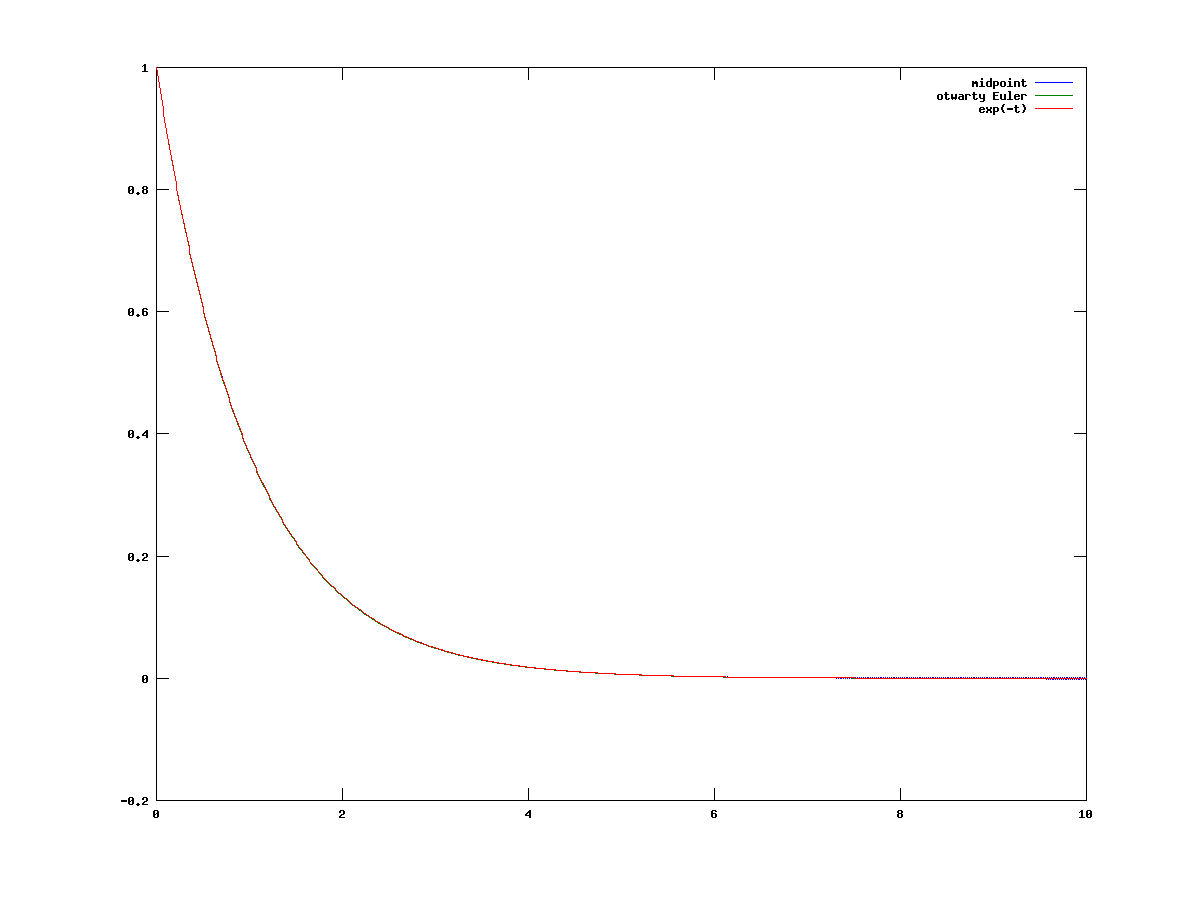
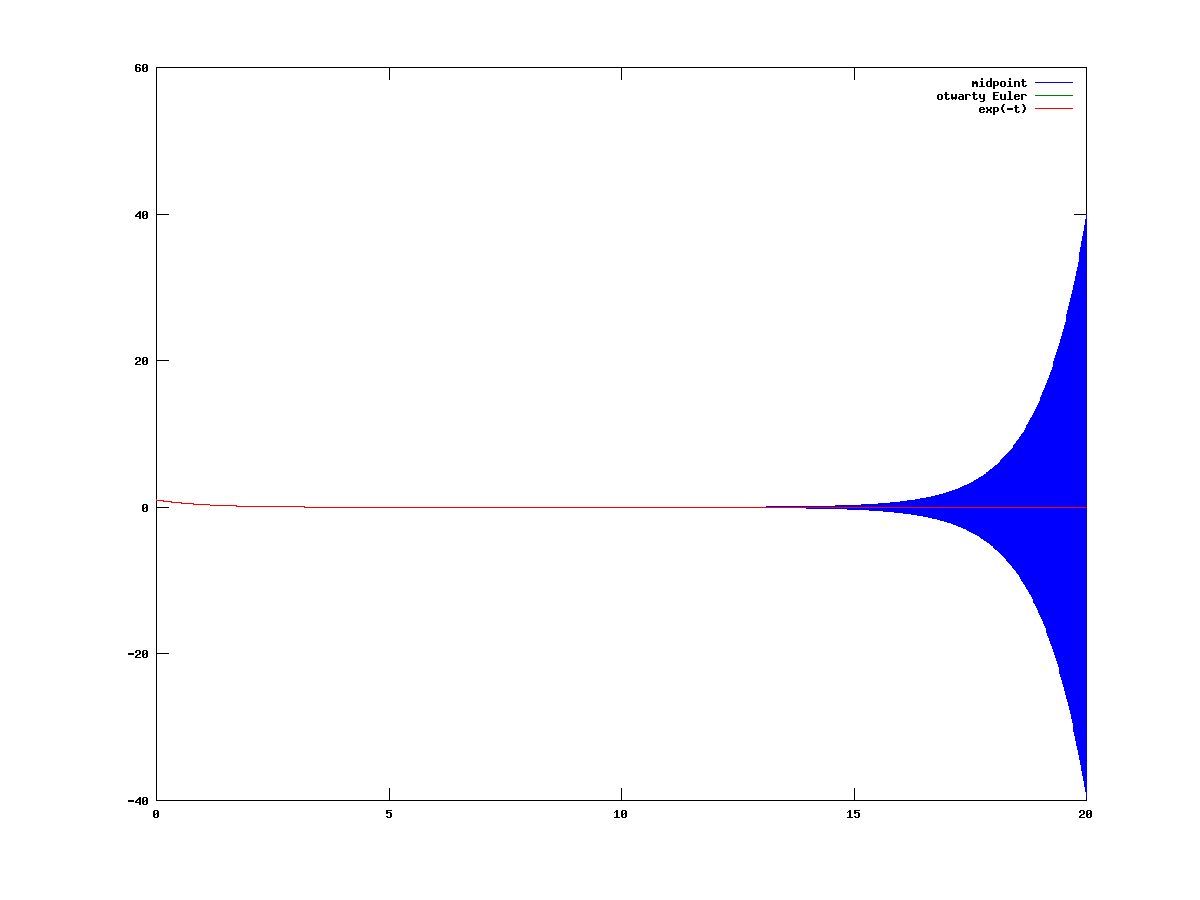
Weźmy mniejsze ![]() . Wtedy na
. Wtedy na ![]() wszystko jest w porządku, ale na odcinku
wszystko jest w porządku, ale na odcinku ![]() znów rozwiązanie otrzymane schematem midpoint zaczyna od pewnego momentu oscylować z coraz większą amplitudą, zamiast maleć do zera. Im
znów rozwiązanie otrzymane schematem midpoint zaczyna od pewnego momentu oscylować z coraz większą amplitudą, zamiast maleć do zera. Im ![]() jest mniejsze, tym odcinek na którym rozwiązanie otrzymane schematem midpoint dobrze aproksymuje rozwiązanie równania wyjściowego jest większy, ale zawsze w pewnym momencie pojawi się zaburzenie numeryczne, por. rysunki 5.3 i 5.4.
jest mniejsze, tym odcinek na którym rozwiązanie otrzymane schematem midpoint dobrze aproksymuje rozwiązanie równania wyjściowego jest większy, ale zawsze w pewnym momencie pojawi się zaburzenie numeryczne, por. rysunki 5.3 i 5.4.
Numeryczne zaburzenie wynika właśnie z tego, że schemat nie jest silnie stabilny. Można wypisać wzór na rozwiązania równania różnicowego zadanego przez schemat midpoint dla tego równania i wykazać, że po jakimś czasie zawsze pojawią się oscylacje.
Wyniki tu otrzymane nie stoją w jakiekolwiek sprzeczności z teorią zbieżności schematów liniowych wielokrokowych.
Można sprawdzić, że schemat midpoint spełnia założenia tej teorii dla tego równania, i że
na ustalonym odcinku ![]() zachodzi zbieżność z rzędem dwa.
W praktyce nie należy stosować schematów, które nie są silnie stabilne, ponieważ zawsze mogą pojawić się oscylacje po a priori nie znanym czasie, szczególnie kiedy chcemy rozwiązać równanie na długim odcinku czasu.
zachodzi zbieżność z rzędem dwa.
W praktyce nie należy stosować schematów, które nie są silnie stabilne, ponieważ zawsze mogą pojawić się oscylacje po a priori nie znanym czasie, szczególnie kiedy chcemy rozwiązać równanie na długim odcinku czasu.
5.3. Wartości startowe schematów wielokrokowych
W tym miejscu warto zwrócić uwagę, jak w praktycznych obliczeniach implementować schematy liniowe wielokrokowe.
Aby przy pomocy danego schematu ![]() -krokowego rzędu
-krokowego rzędu ![]() obliczyć
obliczyć ![]() , należy znać poprzednie
, należy znać poprzednie
![]() przybliżenia
przybliżenia ![]() . Czyli aby wystartować schemat musimy znaleźć odpowiednio dobre (tzn. takie, że
. Czyli aby wystartować schemat musimy znaleźć odpowiednio dobre (tzn. takie, że ![]() , por. Twierdzenie 5.2)
startowe przybliżenia
, por. Twierdzenie 5.2)
startowe przybliżenia ![]() . Wartość
. Wartość ![]() jest zadana jako warunek początkowy, tzn.
możemy przyjąć dany warunek początkowy
jest zadana jako warunek początkowy, tzn.
możemy przyjąć dany warunek początkowy ![]() . Natomiast musimy wyliczyć
. Natomiast musimy wyliczyć
![]() .
W praktyce do wyliczenia tych wartości możemy np. zastosować
.
W praktyce do wyliczenia tych wartości możemy np. zastosować ![]() razy schemat jednokrokowy tego rzędu co najmniej
razy schemat jednokrokowy tego rzędu co najmniej ![]() .
.
Dla schematu Adamsa-Bashfortha dwukrokowego rzędu dwa za ![]() możemy przyjąć
możemy przyjąć ![]() obliczone jednym krokiem schematu Heuna.
Tu warto zauważyć że musimy zastosować tylko jeden krok schematu Heuna. Uwzględniając to widzimy, że
obliczone jednym krokiem schematu Heuna.
Tu warto zauważyć że musimy zastosować tylko jeden krok schematu Heuna. Uwzględniając to widzimy, że ![]() można by też obliczyć stosując dowolny schemat jednokrokowy rzędu jeden np. otwarty schemat Eulera.
Ogólniej do obliczenia startowych wartości
można by też obliczyć stosując dowolny schemat jednokrokowy rzędu jeden np. otwarty schemat Eulera.
Ogólniej do obliczenia startowych wartości ![]() dla schematu
dla schematu ![]() -krokowego rzędu
-krokowego rzędu ![]() można zastosować schemat jednokrokowy rzędu
można zastosować schemat jednokrokowy rzędu ![]() lub większego.
lub większego.
5.4. Eksperymentalne badanie rzędu zbieżności schematów
![\begin{array}[]{|c|c|c|c|c|c|c|}\hline h&otwarty\; Euler&|e_{n}/e_{{n+1}}|&Heun&|e_{n}/e_{{n+1}}|&zmod.\; Euler&|e_{n}/e_{{n+1}}|\\
\hline 2.5e-01&4.61e-02&0.00&1.90e-03&0.00&6.57e-03&0.00\\
1.1e-01&1.98e-02&2.33&3.51e-04&5.40&1.19e-03&5.53\\
5.3e-02&9.23e-03&2.14&7.63e-05&4.60&2.56e-04&4.64\\
2.6e-02&4.47e-03&2.07&1.78e-05&4.28&5.97e-05&4.29\\
1.3e-02&2.20e-03&2.03&4.32e-06&4.13&1.44e-05&4.14\\
6.3e-03&1.09e-03&2.02&1.06e-06&4.07&3.55e-06&4.07\\
3.1e-03&5.44e-04&2.01&2.63e-07&4.03&8.79e-07&4.03\\
1.6e-03&2.71e-04&2.00&6.55e-08&4.02&2.19e-07&4.02\\
\hline\end{array}](wyklady/nrr/mi/mi644.png) |
![\begin{array}[]{|c|c|c|c|c|}\hline h&Heun&|e_{n}/e_{{n+1}}|&rk4&|e_{n}/e_{{n+1}}|\\
\hline 5.3e-01&5.96e+03&&9.09e+01&\\
2.6e-01&1.91e+03&3.12&6.41e+00&14.18\\
1.3e-01&5.29e+02&3.61&4.24e-01&15.12\\
6.3e-02&1.38e+02&3.83&2.73e-02&15.56\\
3.1e-02&3.52e+01&3.92&1.73e-03&15.78\\
1.6e-02&8.88e+00&3.96&1.09e-04&15.89\\
7.8e-03&2.23e+00&3.98&6.81e-06&15.95\\
3.9e-03&5.59e-01&3.99&4.27e-07&15.97\\
2.0e-03&1.40e-01&4.00&2.66e-08&16.02\\
\hline\end{array}](wyklady/nrr/mi/mi591.png) |
Rząd zbieżności schematu dla czasu ![]() można badać eksperymentalnie dla ustalonego zagadnienia początkowego
można badać eksperymentalnie dla ustalonego zagadnienia początkowego ![]() z warunkiem początkowym
z warunkiem początkowym ![]() i ze znanym rozwiązaniem
i ze znanym rozwiązaniem ![]() określonym na odcinku
określonym na odcinku ![]() .
Możemy wtedy przy pomocy naszego schematu, np. schematu Heuna, zmodyfikowanego schematu Eulera i otwartego schematu Eulera
obliczać przybliżone wartości
.
Możemy wtedy przy pomocy naszego schematu, np. schematu Heuna, zmodyfikowanego schematu Eulera i otwartego schematu Eulera
obliczać przybliżone wartości ![]() dla ustalonego
dla ustalonego ![]() , z połowionym krokiem
, z połowionym krokiem ![]() :
:
![]() dla ustalonego
dla ustalonego ![]() . Będziemy badać jak zmienia się błąd w kolejnych krokach, a dokładniej, jak zmienia się stosunek błędów dla kolejnych połowionych
. Będziemy badać jak zmienia się błąd w kolejnych krokach, a dokładniej, jak zmienia się stosunek błędów dla kolejnych połowionych ![]() .
.
Jeśli błąd dla ustalonego ![]() zachowywałby się jak
zachowywałby się jak ![]() , a dokładniej, gdyby
, a dokładniej, gdyby ![]() , to stosunek błędu powinien się zachowywać jak:
, to stosunek błędu powinien się zachowywać jak:
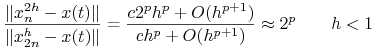 |
dla dostatecznie małych ![]() ,
czyli dla schematów Heuna i zmodyfikowanego schematu Eulera jak cztery, a dla otwartego schematu Eulera jak dwa, a dla schematu rzędu cztery jak
,
czyli dla schematów Heuna i zmodyfikowanego schematu Eulera jak cztery, a dla otwartego schematu Eulera jak dwa, a dla schematu rzędu cztery jak ![]() - czyli szesnaście.
- czyli szesnaście.
W tabeli 5.1 widzimy wyniki eksperymentu dla ![]() dla schematów: otwartego schematu
Eulera, Heuna i zmodyfikowanego schematu Eulera zastosowanych do zagadnienia początkowego
dla schematów: otwartego schematu
Eulera, Heuna i zmodyfikowanego schematu Eulera zastosowanych do zagadnienia początkowego
![]() z
z ![]() , którego rozwiązaniem jest
, którego rozwiązaniem jest ![]() , czyli
, czyli ![]() .
.
W tabeli 5.2 przedstawiliśmy wyniki tego samego eksperymentu, ale dla schematu Rungego-Kutty rzędu cztery dla zadania początkowego ![]() z
z ![]() i dla
i dla ![]() , czyli z rozwiązaniem
, czyli z rozwiązaniem ![]() . Skoro schemat jest rzędu cztery,
możemy oczekiwać, że błąd będzie jak
. Skoro schemat jest rzędu cztery,
możemy oczekiwać, że błąd będzie jak ![]() dla ustalonego
dla ustalonego ![]() .
.
Wyniki uzyskane w tabeli 5.2 potwierdzają nasze przypuszczenie.
Dla kroku o połowę mniejszego błąd maleje około ![]() razy dla dostatecznie małych
razy dla dostatecznie małych ![]() (im
(im ![]() mniejsze, tym ten stosunek bliższy jest szesnastu). Przy okazji zauważmy, jak ogromna jest różnica w błędzie dla
schematu rzędu cztery (Rungego-Kutty), a dla schematu Heuna rzędu dwa.
W przypadku tego ostatniego -
błąd bezwzględny dla
mniejsze, tym ten stosunek bliższy jest szesnastu). Przy okazji zauważmy, jak ogromna jest różnica w błędzie dla
schematu rzędu cztery (Rungego-Kutty), a dla schematu Heuna rzędu dwa.
W przypadku tego ostatniego -
błąd bezwzględny dla ![]() jest rzędu
jest rzędu ![]() , a dla tego pierwszego błąd jest rzędu
, a dla tego pierwszego błąd jest rzędu ![]() .
Z kolei patrząc na błędy względne, w przypadku schematu Heuna błąd jest na poziomie
.
Z kolei patrząc na błędy względne, w przypadku schematu Heuna błąd jest na poziomie ![]() ,
a dla schematu Rungego
,
a dla schematu Rungego ![]() , czyli poziom błędu w arytmetyce podwójnej precyzji praktycznie jest
wystarczająco dokładny.
, czyli poziom błędu w arytmetyce podwójnej precyzji praktycznie jest
wystarczająco dokładny.
Błędem bezwzględnym nazywamy ![]() , a względnym
, a względnym ![]() .
W przypadku gdy
.
W przypadku gdy ![]() jest bardzo duże lub bardzo małe należy rozpatrywać błąd względny choćby z powodu
własności arytmetyki zmiennopozycyjnej.
jest bardzo duże lub bardzo małe należy rozpatrywać błąd względny choćby z powodu
własności arytmetyki zmiennopozycyjnej.
5.5. Zadania
Ćwiczenie 5.1
Zbadaj rząd zbieżności zamkniętego schematu Eulera korzystając z teorii zbieżności dla schematów jednokrokowych.
Ćwiczenie 5.2
Zbadaj rząd zbieżności zamkniętego schematu Eulera korzystając z teorii zbieżności dla schematów wielokrokowych liniowych. Czy schemat jest silnie stabilny?
Ćwiczenie 5.3
Zbadaj rząd zbieżności schematu trapezów dany wzorem (4.7).
-
korzystając z teorii zbieżności dla schematów jednokrokowych,
-
korzystając z teorii zbieżności dla schematów wielokrokowych liniowych.
Czy schemat jest silnie stabilny?
Ćwiczenie 5.4
Zbadaj rząd zbieżności zmodyfikowanego Eulera i schematu Heuna.
Ćwiczenie 5.5
Zbadaj rząd zbieżności schematu punktu środkowego (ang. midpoint). Czy schemat jest silnie stabilny?
Ćwiczenie 5.6 (laboratoryjne)
Zaimplementuj schematy: otwarty i zamknięty Eulera w octave i przetestuj rzędy zbieżności eksperymentalnie metodą połowionego kroku, jak opisano w rozdziale 5.4 dla równania
skalarnego ![]() oraz dla równania drugiego rzędu
oraz dla równania drugiego rzędu ![]() z
z ![]() .
.
Do rozwiązywania nieliniowego równania przy implementacji schematu zamkniętego w każdym kroku możesz użyć funkcji fsolve().
Ćwiczenie 5.7 (laboratoryjne)
Zaimplementuj schemat trapezów, por. (4.7), w octave i przetestuj rząd zbieżności eksperymentalnie metodą połowionego kroku, jak opisano w rozdziale 5.4 dla równania
skalarnego ![]() oraz dla równania drugiego rzędu
oraz dla równania drugiego rzędu ![]() z
z ![]() .
.
Do rozwiązywania nieliniowego równania w każdym kroku możesz użyć funkcji fsolve().
Ćwiczenie 5.8 (laboratoryjne)
Zaimplementuj zmodyfikowany schemat Eulera oraz schemat Heuna w octave i przetestuj rzędy zbieżności eksperymentalnie metodą połowionego kroku, jak opisano w rozdziale 5.4.
Ćwiczenie 5.9 (laboratoryjne)
Zaimplementuj schemat Rungego rzędu cztery, dany wzorem (4.15) w octave i przetestuj rząd zbieżności schematu eksperymentalnie metodą połowionego kroku, jak opisano w rozdziale 5.4.
Ćwiczenie 5.10 (laboratoryjne)
Zaimplementuj schemat (ang. midpoint) w octave i przetestuj rząd zbieżności schematu eksperymentalnie metodą połowionego kroku,
jak opisano w rozdziale 5.4, przyjmując, że
![]() , czyli jest równe dokładnemu rozwiązaniu. Dla równania
, czyli jest równe dokładnemu rozwiązaniu. Dla równania ![]() z
z ![]() zastosuj schemat na długim odcinku czasu dla ustalonego
zastosuj schemat na długim odcinku czasu dla ustalonego ![]() . Czy rozwiązanie zachowuje się tak jak tego oczekujemy? Zmniejsz
. Czy rozwiązanie zachowuje się tak jak tego oczekujemy? Zmniejsz ![]() i zobacz czy sytuacja się poprawia?
i zobacz czy sytuacja się poprawia?
Ćwiczenie 5.11
Zbadaj rząd, stabilność i rząd zbieżności otwartego dwukrokowego schematu Adamsa, por. Ćwiczenie 4.7.
Ćwiczenie 5.12 (laboratoryjne)
Zaimplementuj w octave otwarty dwukrokowy schemat Adamsa, por. Ćwiczenie 4.7.
Następnie przetestuj eksperymentalnie rząd zbieżności tego schematu metodą połowionego kroku,
jak opisano w rozdziale 5.4 dla ![]() z
z ![]() . Biorąc za
. Biorąc za ![]() :
:
-
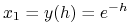 czyli rozwiązanie dokładne dla
czyli rozwiązanie dokładne dla 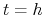 .
. -
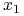 obliczone schematem Heuna czyli schematem Rungego-Kutty rzędu dwa.
obliczone schematem Heuna czyli schematem Rungego-Kutty rzędu dwa. -
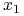 obliczone schematem Eulera otwartym czyli schematem rzędu jeden.
obliczone schematem Eulera otwartym czyli schematem rzędu jeden.
Ćwiczenie 5.13
Znajdź dokładne rozwiązanie ![]() schematu różnicowego, który jest schematem punktu środkowego zastosowanym dla równania
schematu różnicowego, który jest schematem punktu środkowego zastosowanym dla równania ![]() . Pokaż, że jeśli
. Pokaż, że jeśli ![]() , a
, a ![]() różne od jednej konkretnej wartości (co np. odpowiada warunkom startowym
różne od jednej konkretnej wartości (co np. odpowiada warunkom startowym ![]() ), to
), to ![]() , czyli pojawią się niepotrzebne kumulujące się zaburzenia numeryczne.
, czyli pojawią się niepotrzebne kumulujące się zaburzenia numeryczne.
Ćwiczenie 5.14 (trudne)
Udowodnij stwierdzenie 5.1.
Z tego, że rząd schematu jest co najmniej jeden, wynika od razu warunek zgodności schematu (wystarczy rozważyć oba równania ![]() z
z ![]() i
i ![]() z
z ![]() ). Natomiast aby pokazać, że ze zgodności schematu wynika to, że rząd schematu jest większy od jeden,
należy zastosować wzór Taylora.
). Natomiast aby pokazać, że ze zgodności schematu wynika to, że rząd schematu jest większy od jeden,
należy zastosować wzór Taylora.
Ćwiczenie 5.15
Czy schemat Adamsa (por. rozdział 4.1.2) może nie być stabilny, ewentualnie nie być silnie stabilny? Uzasadnij podając ewentualnie kontrprzykład niestabilnego (czy nie będącego silnie stabilnym) schematu Adamsa.