Zagadnienia
9. Metoda różnic skończonych - stabilność schematów dla zadań eliptycznych w normie maksimum
W tym rozdziale zajmiemy się przedstawieniem metod badania stabilności schematów różnicowych dla zadań liniowych w dyskretnej normie maksimum.
Będziemy badali stabilność schematu zapisanego w formie (8.5)-(8.6).
Dla ![]() możemy zapisać (8.5) jako:
możemy zapisać (8.5) jako:
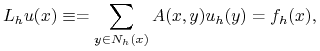 |
(9.1) |
gdzie ![]() jest podzbiorem
jest podzbiorem ![]() punktów, dla których
punktów, dla których ![]() ,
czyli uwzględnionych w równaniu dla tego
,
czyli uwzględnionych w równaniu dla tego ![]() .
.
Jeśli ![]() , to dla (8.6) zachodzi:
, to dla (8.6) zachodzi:
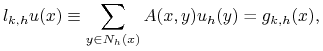 |
gdzie ![]() jest zdefiniowane analogicznie jak poprzednio.
jest zdefiniowane analogicznie jak poprzednio.
![]() jest zdefiniowane jednoznacznie.
jest zdefiniowane jednoznacznie.
![]() nazywamy otoczeniem siatkowym punktu
nazywamy otoczeniem siatkowym punktu ![]() . Wprowadzimy również otoczenie siatkowe nakłute:
. Wprowadzimy również otoczenie siatkowe nakłute: ![]() .
Oczywiście
.
Oczywiście ![]() może być jednopunktowe, wtedy
może być jednopunktowe, wtedy ![]() jest zbiorem pustym.
jest zbiorem pustym.
Zapiszmy schemat (8.5)-(8.6) jako:
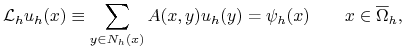 |
(9.2) |
gdzie
Wtedy zachodzi następujące twierdzenie, pozwalające na wykazanie stabilności niektórych schematów w normie dyskretnej maksimum:
Twierdzenie 9.1
Niech ![]() dla (8.5)-(8.6) będzie w formie (9.2).
Załóżmy, że dla pewnej stałej
dla (8.5)-(8.6) będzie w formie (9.2).
Załóżmy, że dla pewnej stałej ![]() i dla
i dla ![]() :
:
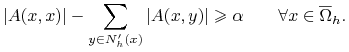 |
Wtedy
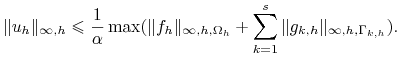 |
Widzimy, że ![]() dla pewnego
dla pewnego
![]() .
.
Rozpatrzmy równanie ze schematu dla tego punktu:
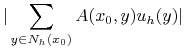 |
||||
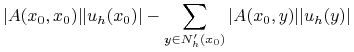 |
||||
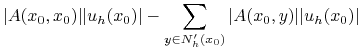 |
||||
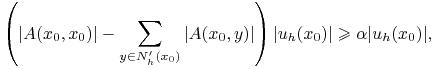 |
czyli
Przykład 9.1
Dla zadania (7.5)-(7.6) otrzymujemy następujący układ:
dla ![]() .
.
Zatem ![]() dla
dla ![]() i
i ![]() dla
dla ![]() , tzn. dla
, tzn. dla ![]() .
Sprawdzamy założenie twierdzenia:
.
Sprawdzamy założenie twierdzenia:
![|A(x_{k},x_{k})|-\sum _{{y\in N_{h}(x_{k})\setminus\{ x_{k}\}}}|A(x_{k},y)|=\left\{\begin{array}[]{lcr}c&&k=1,\ldots,N-1\\
1&&k=0,N.\end{array}\right.](wyklady/nrr/mi/mi1340.png) |
Zatem ![]() i z naszego kryterium, tzn. z twierdzenia 9.1,
otrzymujemy stabilność zadania przybliżonego w normie dyskretnej supremum tylko w przypadku
i z naszego kryterium, tzn. z twierdzenia 9.1,
otrzymujemy stabilność zadania przybliżonego w normie dyskretnej supremum tylko w przypadku ![]() ze stałą
ze stałą ![]() .
.
Powyższe oszacowanie sugeruje, że jeśli ![]() , to schemat może nie być stabilny w dyskretnej normie maksimum.
Okaże się, że istnieją jednak inne kryteria badania stabilności, które są bardziej precyzyjne.
Przedstawimy je poniżej.
, to schemat może nie być stabilny w dyskretnej normie maksimum.
Okaże się, że istnieją jednak inne kryteria badania stabilności, które są bardziej precyzyjne.
Przedstawimy je poniżej.
9.1. Różnicowa zasada maksimum
Jak wiadomo, por. np. rozdział 6.4 w [11], dla równania eliptycznego spełnionych jest szereg zasad maksimum. Okaże się, że odpowiednio skonstruowane schematy różnicowe, czyli problemy przybliżone (różnicowe), spełniają analogiczne różnicowe zasady maksimum. Korzystając z tych zasad będziemy mogli wykazać stabilność tychże schematów.
Załóżmy, że operator ![]() określony na
określony na ![]() jest w formie (9.2).
jest w formie (9.2).
Definicja 9.1
Operator ![]() w postaci (9.2) będziemy nazywać operatorem dodatniego typu (ang. positive operator) w
w postaci (9.2) będziemy nazywać operatorem dodatniego typu (ang. positive operator) w ![]() , jeśli dla dowolnego
, jeśli dla dowolnego ![]()
-
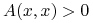 ,
, -
 ,
, -
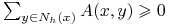 .
.
Dodatkowo dla operatora typu dodatniego przedstawiamy siatkę ![]() jako dwa rozłączne zbiory
jako dwa rozłączne zbiory ![]() zdefiniowane jako:
zdefiniowane jako:
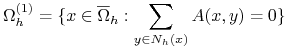 |
i
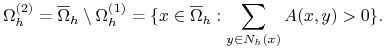 |
Wprowadzamy jeszcze jedną definicję:
Definicja 9.2
Załóżmy, że ![]() w postaci (9.2) jest operatorem dodatniego typu w
w postaci (9.2) jest operatorem dodatniego typu w ![]() , dla którego zachodzi warunek:
, dla którego zachodzi warunek: ![]() i
i ![]() jest zbiorem skończonym. Wtedy powiemy, że
jest zbiorem skończonym. Wtedy powiemy, że ![]() spełnia warunek spójności siatki (ang. mesh connectivity condition, mesh is connected), jeśli
dla dowolnego
spełnia warunek spójności siatki (ang. mesh connectivity condition, mesh is connected), jeśli
dla dowolnego ![]() istnieje ciąg elementów siatki
istnieje ciąg elementów siatki ![]() i
i ![]() taki, że
taki, że
![]() , i
, i ![]() dla
dla ![]() i
i ![]() .
.
Wtedy zachodzi następująca różnicowa zasada maksimum:
Twierdzenie 9.2 (Różnicowa zasada maksimum - ang. finite difference maximum principle)
Załóżmy, że ![]() w postaci (9.2) jest operatorem dodatniego typu w
w postaci (9.2) jest operatorem dodatniego typu w ![]() , i że
, i że ![]() jest zbiorem skończonym spełniającym warunek spójności siatki.
Wtedy, jeśli
jest zbiorem skończonym spełniającym warunek spójności siatki.
Wtedy, jeśli
to
Dowód można znaleźć w Rozdziale 10 w [10].
Wniosek 9.1
Załóżmy, że spełnione są założenia twierdzenia 9.2. Wtedy zadanie (9.2) ma jednoznaczne rozwiązanie.
Załóżmy, że zadanie (9.2) ma dwa różne rozwiązania ![]() dla
dla ![]() . Wtedy
z twierdzenia 9.2
wynika, że
. Wtedy
z twierdzenia 9.2
wynika, że ![]() zatem
zatem ![]() ale i
ale i ![]() , czyli
, czyli ![]() .
Z kolei zauważmy, że (9.2) jest układem równań liniowych, więc
jednoznaczność rozwiązania z prawą stroną równą zero jest równoważna istnieniu rozwiązania dla dowolnego
.
Z kolei zauważmy, że (9.2) jest układem równań liniowych, więc
jednoznaczność rozwiązania z prawą stroną równą zero jest równoważna istnieniu rozwiązania dla dowolnego ![]() .
.
Jako kolejny wniosek z różnicowej zasady maksimum otrzymujemy następujące kryterium porównawcze:
Z ostatniego twierdzenia otrzymujemy następujące kryterium badania stabilności w dyskretnej normie maksimum:
Twierdzenie 9.4 (kryterium stabilności z różnicowej zasady maksimum)
Załóżmy, że spełnione są założenia twierdzenia 9.2
oraz, że istnieje nieujemna funkcja ![]() określona na
określona na ![]() taka,że
taka,że
Wtedy ![]() - rozwiązanie (9.2) z prawą stroną
- rozwiązanie (9.2) z prawą stroną ![]() , spełnia:
, spełnia:
Dla prostoty załóżmy, że ![]() (
(![]() jest liniowe, więc
zawsze możemy przeskalować
jest liniowe, więc
zawsze możemy przeskalować ![]() i
i ![]() przez stałą różną od zera).
Wtedy
przez stałą różną od zera).
Wtedy
zatem z twierdzenia 9.3 otrzymujemy:
Przykład 9.2
Powróćmy do dyskretyzacji naszego modelowego zadania, tzn. do (7.5)-(7.6).
Pozostawiamy jako proste zadanie sprawdzenie, że operator ![]() w tym przypadku jest operatorem dodatniego typu, i że siatka spełnia warunek spójności.
w tym przypadku jest operatorem dodatniego typu, i że siatka spełnia warunek spójności.
Aby pokazać oszacowanie stabilności korzystając z naszego kryterium należy znaleźć funkcję
nieujemną ![]() określoną na
określoną na ![]() , czyli w szczególności na każdej siatce ograniczonej, taką że
, czyli w szczególności na każdej siatce ograniczonej, taką że
Na brzegu widzimy, że ![]() dla
dla ![]() , więc wystarczy przyjąć
, więc wystarczy przyjąć ![]() takie, że
takie, że ![]() na brzegu
na brzegu ![]() .
.
Najprościej będzie znaleźć funkcję ![]() taką, że
taką, że ![]() .
Następnie, korzystając
z tego, że rząd aproksymacji zadania przybliżonego jest dwa w każdym punkcie siatki, tzn.
.
Następnie, korzystając
z tego, że rząd aproksymacji zadania przybliżonego jest dwa w każdym punkcie siatki, tzn.
możemy wywnioskować, że istnieje stała ![]() taka, że dla
taka, że dla ![]() funkcja
funkcja
spełnia ![]() .
.
W naszym przypadku np. dla ![]() wystarczy zdefiniować:
wystarczy zdefiniować:
Wtedy ![]() i
i ![]() .
Zatem z naszego kryterium otrzymujemy dla
.
Zatem z naszego kryterium otrzymujemy dla ![]() , że
, że
czyli stabilność w dyskretnej normie maksimum.
Proszę zauważyć, że
stała w oszacowaniu nie zależy od stałej ![]() , za to - inaczej niż w przypadku poprzedniego prostszego kryterium, zależy od długości odcinka
, za to - inaczej niż w przypadku poprzedniego prostszego kryterium, zależy od długości odcinka ![]() .
.
Jeśli rozwiązanie
(7.1) jest w ![]() , to otrzymujemy, że:
, to otrzymujemy, że:
dla ![]() z (8.7),
a warunki brzegowe spełnione są dokładnie.
Zatem, korzystając z twierdzenia 8.1, otrzymujemy:
z (8.7),
a warunki brzegowe spełnione są dokładnie.
Zatem, korzystając z twierdzenia 8.1, otrzymujemy:
9.2. Zadania
Ćwiczenie 9.1
Zbadaj stabilność schematu (8.10) dyskretyzacji modelowego problemu dwuwymiarowego
w dyskretnej normie maksimum dla ![]() .
.
Ćwiczenie 9.2
Sprawdź, czy operator z (8.10) jest dodatniego typu i
zbadaj stabilność schematu (8.10) dyskretyzacji modelowego problemu dwuwymiarowego
w dyskretnej normie maksimum dla ![]() korzystając z różnicowej zasady maksimum.
korzystając z różnicowej zasady maksimum.
Ćwiczenie 9.3
Rozpatrzmy problem ![]() dla
dla ![]() i
i ![]() gładkiej funkcji z warunkiem brzegowym Neumanna
gładkiej funkcji z warunkiem brzegowym Neumanna
![]() dla
dla ![]() oraz schemat różnicowy na siatce jednorodnej
oraz schemat różnicowy na siatce jednorodnej ![]() dla
dla ![]() :
:
z ![]() .
Czy to zadania wyjściowe oraz zadanie dyskretne mają jednoznaczne rozwiązanie dla
.
Czy to zadania wyjściowe oraz zadanie dyskretne mają jednoznaczne rozwiązanie dla ![]() ?
?
Zbadaj rząd tego schematu oraz stabilność w dyskretnej normie maksimum dla stałej ![]() . Podaj oszacowanie błędu dyskretnego w dyskretnej
normie maksimum w terminach
. Podaj oszacowanie błędu dyskretnego w dyskretnej
normie maksimum w terminach ![]() .
.
Ćwiczenie 9.4
Zbadaj rząd i stabilność w normie maksimum schematu skonstruowanego analogicznie jak schemat (8.10) dyskretyzacji modelowego problemu dwuwymiarowego: ![]() w
w ![]() z zerowym warunkiem Dirichleta
na brzegu kwadratu oprócz krawędzi
z zerowym warunkiem Dirichleta
na brzegu kwadratu oprócz krawędzi ![]() , gdzie jest postawiony zerowy warunek
brzegowy Neumanna tzn.
, gdzie jest postawiony zerowy warunek
brzegowy Neumanna tzn. ![]() dla
dla ![]() i
i ![]() na
na ![]() .
.
Warunek brzegowy na ![]() przybliżamy w schemacie różnicowym przez odpowiednią różnicę skończoną wprzód, tzn.
przez
przybliżamy w schemacie różnicowym przez odpowiednią różnicę skończoną wprzód, tzn.
przez ![]() dla
dla ![]() z
z ![]() .
.
Ćwiczenie 9.5
Zbadaj stabilność w dyskretnej normie maksimum schematu z ćwiczenia 8.6.
Ćwiczenie 9.6
Zbadaj stabilność w dyskretnej normie maksimum schematu z ćwiczenia 8.9.




