Zagadnienia

12.1 Pierwsze błędne symulacje
- To, że program działa, nie znaczy jeszcze, że działa tak, jak byśmy chcieli
12.2 Kłopotliwe pytania
12.3 Ponure konstatacje
12.4 Światełko w tunelu

12. Czy te symulacje mogą kłamać?

Symulacje komputerowe na dobre zadomowiły się w wielu dziedzinach badań naukowych, a tym bardziej w zastosowaniach modelowania matematycznego. Ufamy — ludzie matematyki stosowanej — wynikom symluacji tak bardzo, że przestaliśmy głośno wątpić w ich poprawność. Doszło do tego, że w pracach naukowych dotyczących analizy konkretnych modeli matematycznych rzeczywistości nagminnie pomija się szczegóły dokonanych obliczeń (zastępując je — jeśli w ogóle — zdawkowym ,,…wyniki komputerowych symulacji wykazują, że…”). Gdy porównamy to ze szczegółowym opisem narzędzi badawczych, technik pomiarowych i procedury eksperymentów, który jest nieodłączną częścią poważnych prac naukowych, będziemy mogli lepiej pojąć stopień bałwochwalczego uwielbienia i bezgranicznej ufności, jaką współcześni badacze obdarzają narzędzia i procedury prowadzenia eksperymentów obliczeniowych.

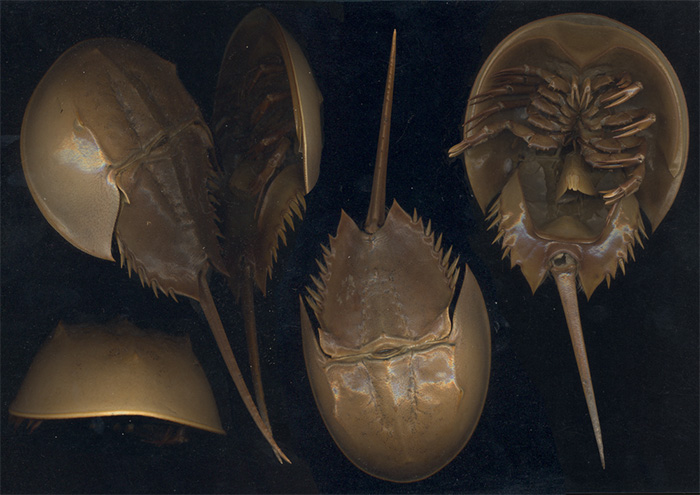
Ze względu na wygląd, skrzypłocze po angielsku nazywa się horeseshoe crab, czyli krab-podkowa. Należą do rzędu ostrogonów, z powodu odwłoka w kształcie długiego kolca (miecza)

Występujący w Oceanie Atlantyckim stawonóg, o nazwie skrzypłocz

(Źródło: Wikipedia)

Aby w życiu zawodowym uniknąć takiego — zdecydowanie niewłaściwego — stosunku do obliczeń naukowych, proponuję na zakończenie ,,zbadać” metodami komputerowymi kolejny model matematyczny: tym razem będzie to model reakcji oka skrzypłocza na światło, zaczerpnięty z pracy [5]³³Dziękuję p. Wandzie Niemyskiej za przedstawienie modelu i wskazanie literatury.. Jest to układ $N$ równań różniczkowych na $[0,T]$ postaci

$\displaystyle y_{r}^{{\prime}}+y_{r}(1+y_{N})=y_{{r-1}},\qquad r=1,\ldots,N.$

(12.1)

(Jak zwykle w modelowaniu matematycznym, powyższe eleganckie równanie jest efektem wcześniejszych sprytnych manipulacji wzorami i dewymiarowania oryginalnego układu równań). Zadana z góry funkcja $y_{0}(t)$ ma modelować przebieg natężenia światła zewnętrznego w czasie. W [5] jest to funkcja schodkowa, przyjmiemy więc konkretnie, że dla $t\in[0,T]$ i zadanych czasów krytycznych $T_{1}<\ldots<T_{N}\in[0,T]$

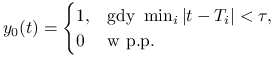$y_{0}(t)=\begin{cases}1,&\text{gdy }\min _{i}|t-T_{i}|<\tau,\\ 0&\text{w p.p.}\end{cases}$

(por. rysunek 12.1).

Jest to funkcja kawałkami stała, generalnie równa zero, z wyjątkiem krótkich okresów, gdy przyjmuje nagle wartość 1.

Rys. 12.1. Przykładowy wykres funkcji $y_{0}(t)$ , gdy $T_{i}=0,1,2,\ldots$ i $\tau=0.1$ .

Dodatkowo powinniśmy przyjąć, że $\tau$ jest małe. Dla badaczy interesująca jest przede wszystkim składowa $y_{N}(t)$ rozwiązania, modelująca odpowiedź oka na bodziec.

Oryginalna praca [5] była na tyle stara, by — oprócz szczegółów sposobu przeprowadzania pomiarów fizycznych, służących jako porównawczy materiał eksperymentalny — wskazać użyte narzędzia obliczeniowe; oto one [5, strona 257]:

Solutions […] were obtained on EDSAC 2 at Cambridge using a Runge–Kutta method.

Każdy, kto choć trochę liznął metod numerycznych rozwiązywania równań różniczkowych zwyczajnych, natychmiast będzie miał wątpliwości: którą konkretnie metodę Rungego–Kutty mają na myśli autorzy? czy klasyczną metodę czteropoziomową, czy może tańszą, dwupoziomową? A może którąś z metod RKF (o ile mamy w ogóle świadomość istnienia takiego wariantu metody Rungego–Kutty…)? Czy stosowano automatyczne sterowanie długością kroku — jeśli tak, to na podstawie jakiego kryterium? A jeśli nie, to jakiej użyto długości kroku całkowania?

12.1. Pierwsze błędne symulacje

Na tym etapie nie wydaje się, by powyższe równanie mogło sprawić nam (to znaczy: naszemu systemowi obliczeń numerycznych) jakikolwiek poważniejszy problem. Wystarczy skorzystać z gotowych narzędzi rozwiązywania równań różniczkowych zwyczajnych dostępnych w Octave (lub w MATLABie): na przykład, z solvera ode45 zaimplementowanego w obu wspomnianych systemach obliczeń naukowych.

W naszych obliczeniach przyjmiemy na początek następujące wartości liczbowe parametrów zadania:

Parametr	Wartość
$N$	10
$T$	3
$\tau$	0.2

Rozwiązanie problemu i wizualizacja składowej $y_{N}$ mogłaby być na przykład zrealizowana poniższym, całkiem standardowym kodem:

Jeśli chcesz pracować w serwisie internetowym WebOctave, najpierw musisz zdefiniować funkcje prawej strony rhs oraz v0.

function dY = rhs(t,Y)
% prawa strona rownania
N = length(Y);
q = [y0(t); Y(1:N-1)];
dY = -Y*(1+Y(N)) + q;
end

function v = y0(t)
% wymuszenie zewnetrzne; t musi byc skalarem!
global tau;
global Ti;
v = (min(abs(t - Ti)) < tau); % krótkie ($2\tau$) pulsy wokół $T_i$
end

Program działa w Octave i wydaje się, że produkuje poprawne wyniki ( $y_{N}$ stabilizuje się), ale już dla $T=153$ obserwujemy ciekawe zjawisko: wyznaczone rozwiązanie wykazuje zachowanie oscylacyjne!

Ćwiczenie 12.1

W symulacji powyżej połóż $T=153$ i sprawdź wyniki. Jak wygląda przebieg wszystkich składowych rozwiązania w czasie?

A więc mamy ,,numeryczny dowód”, że oczy skorupiaka (przynajmniej w ramach naszego modelu), poddane pulsacyjnemu działania światła zewnętrznego, reagują także w sposób periodyczny — co zasadniczo nie powinno nas dziwić… Warto więc byłoby zbadać okres tej reakcji, a następnie spróbować odnieść to zachowanie do wyników eksperymentów fizycznych. Jednak… fizyczny eksperyment nie może być przeprowadzony w tak długim czasie, pozostaje więc nam poruszać się na gruncie teorii.

To, że program działa, nie znaczy jeszcze, że działa tak, jak byśmy chcieli

Gdybyśmy byli nieco bardziej ostrożni, zauważylibyśmy (być może), iż nieco nadużyliśmy składni funkcji ode45. Dokładniej, aby skorzystać z automatycznego sterowania długością kroku w tym solverze, powinniśmy³⁴Wystarczy przeczytać opis funkcji! — nieco inaczej niż w lsode — podać jako drugi argument jedynie dwuelementowy wektor $[0,T]$ ! W przeciwnym razie, solver zawsze wybiera stały krok długości tsmpl(i)-tsmpl(i-1), co przy $T\approx 150$ daje krok całkowania $\approx 0.5$ — zdecydowanie za duży, na przykład, w porównaniu z $\tau\approx 0.2$ !

Ćwiczenie 12.2

Sprawdź, jak zmienią się rozwiązania, gdy układ równań różniczkowych (12.1) zastąpimy układem postaci [5]

$y_{r}^{{\prime}}+y_{r}e^{{y_{N}}}=y_{{r-1}},\qquad r=1,\ldots,N.$

Przeprowadź symulacje i zweryfikuj ich wyniki. A może da się coś konkretnego powiedzieć na gruncie matematycznej teorii, korzystając z faktu, że (w jakimś sensie) $e^{y}\approx 1+y$ ?

12.2. Kłopotliwe pytania

Po rozwiązaniu zagadki oscylacji — nieistniejących w rzeczywistości — możemy teraz mieć ochotę na zabawę z wartością parametru $\tau$ , określającego długość trwania impulsu świetlnego. Z punktu widzenia modelowania, interesujące byłoby wyznaczenie wartości $\tau$ , przy której bezwładność oczu stwora jest na tyle duża, że przestają one reagować na (najwyraźniej zbyt krótkie) impulsy świetlne i ich reakcja wygasa.

W tym celu wystarczy stopniowo zmniejszać $\tau$ i obserwować, jak zmieni się odpowiedź układu; dla wystarczająco krótkich impulsów spodziewamy się, że bodźce będą zbyt słabe, by stabilnie wzbudzić niezerową wartość składowej $y_{N}$ : spodziewamy się $y_{N}$ gasnących do zera.

Przeprowadźmy zatem symulację dla $\tau=10^{{-2}}$ — to znaczy dwudziestokrotnie mniejszej niż dotychczas.

Jak można zorientować się z przeprowadzonej symulacji, początkowo $y_{N}$ rośnie (eksponencjalnie?) i nie wiadomo, czy potem stabilizuje się, jak poprzednio, czy też może zachowanie jest inne. Dlatego należy wydłużyć czas symulacji:

Okazuje się, że faktycznie, rozwiązania $y_{N}$ po chwilowym wzbudzeniu szybko gasną do zera. Aby upewnić się, czy nie mamy czasami do czynienia z numerycznym artefaktem, rozwiążemy to samo równanie, drastycznie zaostrzając kryteria tolerancji błędu, używając do tego funkcji odeset.

Jak widać, choć otrzymane krzywe nie pokrywają się idealnie, zgadzają się ze sobą co do charakteru: $y_{N}$ , po chwilowym wzroście, gaśnie do zera.

Gdybyśmy jednak wykazali mniej zaufania do wyników i rozwiązali zadanie… innym solverem, na przykład ode78 (dostępny w Octave, w MATLABie możesz wybrać na przykład ode115)?

Ćwiczenie 12.3

Wykonaj powyższą symulację z innym solverem.

Wskazówka:

Jeśli będziesz pracować z lsode, pamiętaj o tym, że wymaga on innej składni wywołania oraz innej składni funkcji prawej strony!

Może okazać się, że otrzymamy zupełnie inny wykres! Co prawda pragmatycy staraliby się podkreślić, że ,,co do charakteru” dalej mamy zgodność, bo rozwiązania gasną (do zera?), ale większość z nas, widząc wykresy jak na rysunku 12.2, zaczęłaby powątpiewać w jakość prowadzonych obliczeń.

Rys. 12.2. Porównanie wykresów $y_{N}(t)$ dla $\tau=10^{{-2}}$ , wyznaczonych różnymi solverami, dla $T=130$ .

Może jednak problem leży w tym, że impulsy są na tyle krótkie, że nasz solver, stosując pewne strategie doboru kroku całkowania ,,opuszcza” część impulsu tak, że to z tego powodu rozwiązania gasną?

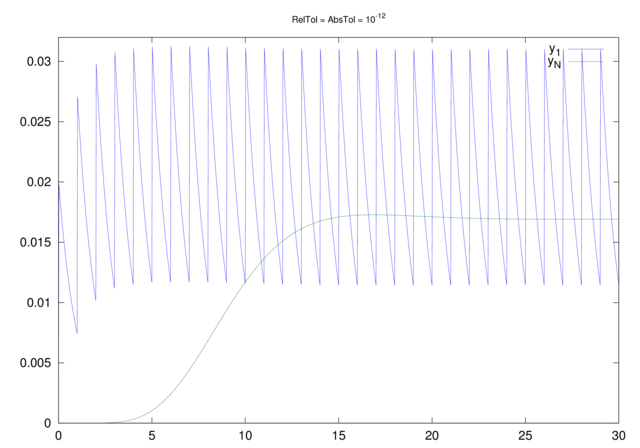
Gdyby bowiem zastosować jeszcze bardziej drastyczne parametry tolerancji błędu, na przykład

odeset('RelTol',1e-12,'AbsTol', 1e-12)

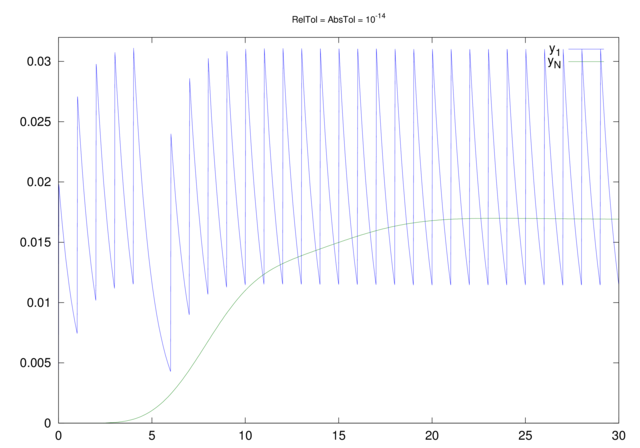
to okazuje się, że co prawda czas obliczeń wydłuża się niepokojąco, ale też i wynik obliczeń zmienia się nie do poznania, zob. wykres 12.3.

Rys. 12.3. Wykres $y_{1}(t)$ i $y_{N}(t)$ dla $\tau=10^{{-2}}$ , wyznaczony przy bardziej wyśrubowanych parametrach tolerancji błędu, solverem ode45..

Po doświadczeniu z większymi $\tau$ bylibyśmy zapewne skłonni uwierzyć bez zastrzeżeń, że otrzymaliśmy wynik wykazujący, że dla $\tau=10^{{-2}}$ rozwiązania jednak nie zanikają w czasie.

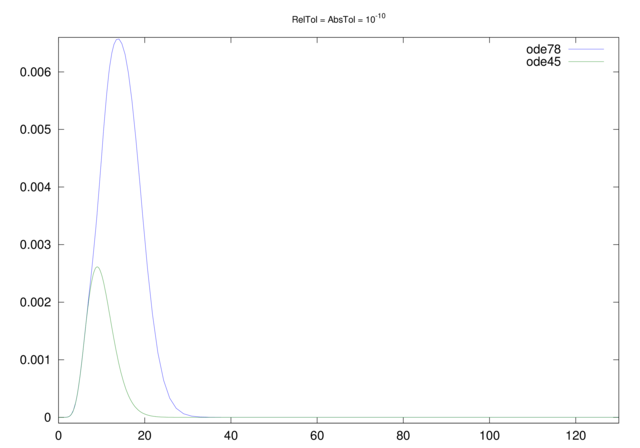
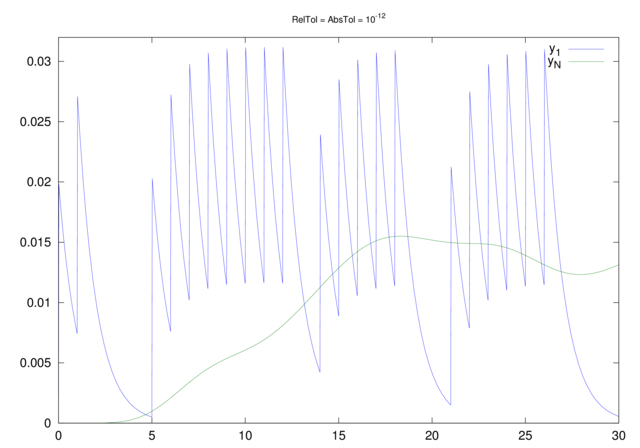
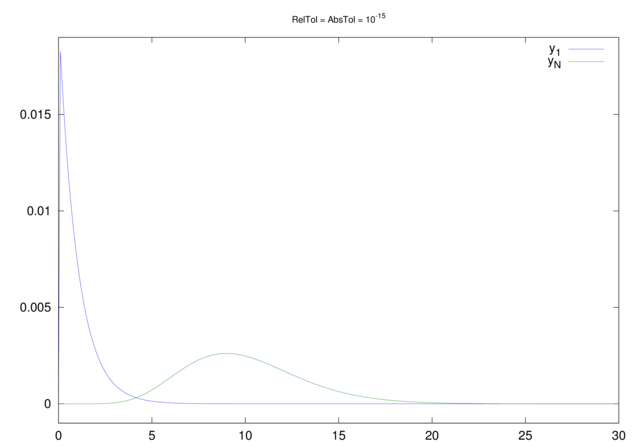
Ale, jeśli przeprowadzilibyśmy symulację korzystając z dokładniejszej metody, ode78 i równie ostrych parametrach tolerancji błędu jak ostatnio, to zapewne zaskoczyłby nas przebieg tak wyznaczonego rozwiązania, przedstawiony na rysunku 12.4.

Rys. 12.4. Wykres $y_{1}(t)$ i $y_{N}(t)$ dla $\tau=10^{{-2}}$ , wyznaczony przy bardziej wyśrubowanych parametrach tolerancji błędu, przez solver wyższego rzędu..

Bardzo możliwe, że jednak za bardzo przejęliśmy się narzędziami, a za mało samym problemem: przecież rozwiązania, które nas interesują, są bardzo mało regularne! A to z kolei znaczy, że stosowanie solvera wysokiego rzędu aproksymacji — takiego jak ode78 — nie bardzo ma sens; rzeczywiście, dla parametrów tolerancji błędu $10^{{-14}}$ , wyniki symulacji (prawie) pokrywają się (por. rysunki 12.5 i 12.6: nie tylko dla obu dotychczas przez nas próbowanych solverów, ale także dla lsode, który wykorzystuje nie tylko zmiany długości kroku, ale także dostosowuje rząd metody.

Rys. 12.5. Wykres $y_{N}(t)$ dla $\tau=10^{{-2}}$ , wyznaczony przy jeszcze bardziej wyśrubowanych parametrach tolerancji błędu, przez solver wyższego rzędu, ode78..

Rys. 12.6. Wykres $y_{N}(t)$ dla $\tau=10^{{-2}}$ , wyznaczony przy średnio wyśrubowanych parametrach tolerancji błędu, przez inny solver, zmiennego rzędu, lsode..

A jak Ty uważasz, poniżej jakiej wartości $\tau$ rozwiązania $y_{N}$ naprawdę dążą do zera, gdy $t\rightarrow\infty$ ?

12.3. Ponure konstatacje

Zauważmy, że nasze zadanie jest mimo wszystko trudne do rozwiązania numerycznego! Wiąże się to z charakterem nieliniowości prawej strony równania, a dokładniej, z przebiegiem $y_{0}(t)$ , która jest funkcją nieciągłą. Wszystkie używane przez nas metody (w postaci solverów typu ode45) zakładają tymczasem, że aproksymowane rozwiązania są funkcjami dostatecznie gładkimi, co oczywiście w naszym przypadku nie jest założeniem spełnionym. To typowa dla obliczeń naukowych sytuacja, gdy istniejące oprogramowanie (i zaimplementowane w nim metody numeryczne) zmuszamy do pracy w warunkach wykraczających poza ich założone zastosowanie.

Gdyby na nasz problem rzucić okiem praktyka, natychmiast zwróciłby nam uwagę na to, że w ,,trudnej” wersji zadania (dla małych $\tau$ ) występują dwie skale czasowe: skala szybkozmienna, związana z zewnętrznymi impulsami i skala wolnozmienna, reakcji $y_{N}$ na wymuszenie. To zaś podpowiada nam, by w takiej sytuacji zastosować krok całkowania krótszy niż długość najkrótszej skali czasowej zadania.

Rozwiązaniem siłowym byłoby więc zmuszenie solvera do pracy z krokiem czasowym wyraźnie mniejszym niż $\tau$ . Jednak z drugiej strony oznacza to nieprawdopodobne zwiększenie kosztu obliczeniowego potrzebnego do wyznaczenia rozwiązania: dla $T=10$ i $\tau=10^{{-3}}$ musielibyśmy wykonać co najmniej $10^{5}$ kroków czasowych (zapewne znacznie więcej).

I faktycznie, o ile uzyskanie (najprawdopodobniej) błędnego wykresu $y_{N}$ wymagało tylko kilku- kilkunastu sekund cierpliwości, to wygenerowanie (bliższego prawdy, miejmy nadzieję) wykresu $y_{N}$ kodem:

opts = odeset('RelTol', 1e-10, ...
	'AbsTol', 1e-10, ...
	'MaxStep', tau, ... % redukcja kroku całkowania do najmniejszej skali czasowej
	'InitialStep', tau/3);
[tcomp, Y] = ode45(@rhs, [0,T], Y0, opts);

ciągnie się niemalże w nieskończoność (sprawdź, ile herbat zdążysz sobie przyrządzić, gdy $\tau=10^{{-4}}$ …).

Czy można byłoby więc jakoś temu zapobiec?

12.4. Światełko w tunelu

Musimy raz jeszcze spojrzeć na naturę naszych kłopotów. Wszystko zdaje się pochodzić stąd, że solvery, których używamy, dobrze działają, gdy rozwiązania są gładkie. Tymczasem nasze rozwiązania są niegładkie. No dobrze, ale przecież tym samym jest to nie tylko problem obliczeniowy, ale także problem czysto matematyczny: jak bowiem zdefiniować rozwiązania równania różniczkowego, w którym prawa strona jest… nieciągła?!

W naszym przypadku, ściślej rzecz biorąc, prawa strona jest kawałkami stała — ciągła z wyjątkiem punktów postaci $T_{i}\pm\tau$ — zatem, gdyby ograniczyć się do przedziałów postaci

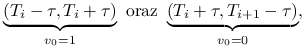$\underbrace{(T_{{i}}-\tau,T_{{i}}+\tau)}_{{v_{0}=1}}\text{ oraz }\underbrace{(T_{i}+\tau,T_{{i+1}}-\tau)}_{{v_{0}=0}},$

tam moglibyśmy sensownie zdefiniować nasze równanie różniczkowe (za wartość początkową w danym przedziale biorąc wartość końcową z przedziału poprzedniego). Gdybyśmy więc postąpili identycznie w naszych obliczeniach, całkowicie uniknęlibyśmy w ten sposób kłopotów z nieciągłościami $v_{0}$ i ich automatyczną lokalizacją! Ceną za to jest wbudowanie w program pętli po pododcinkach, jednak — jak sami za chwilę się przekonamy — będzie warto ją zapłacić!

opts = odeset('RelTol', RTOL, ...
	'AbsTol', ATOL, ...
	'InitialStep', tau/3);
tcomp = []; Y = []; Y0i = Y0;
for i = 1:length(Ti)-1
	opts = odeset(opts, 'MaxStep', (Ti(i+1)-Ti(i))*0.1);
	[tcompi, Yi] = ode45(@rhs, [Ti(i),Ti(i+1)-tau], Y0i, opts);
	tcomp = [tcomp; tcompi];
	Y = [Y; Yi];
	Y0i = Yi(end,:);

	opts = odeset(opts, 'MaxStep', tau*0.1);
	[tcompi, Yi] = ode45(@rhs, [Ti(i+1)-tau,Ti(i+1)], Y0i, opts);
	tcomp = [tcomp; tcompi];
	Y = [Y; Yi];
	Y0i = Yi(end,:);
end
I = Y(:,1); V = Y(:,N);
plot(tcomp,[I,V]);

Ćwiczenie 12.4

Czy teraz jesteś w stanie zbadać zależność $y_{N}$ ,,przy $t\rightarrow\infty$ ” dla różnych $0\leq\tau\leq 1$ ? Jaką możesz postawić hipotezę? Czy potrafisz ją udowodnić?

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.