Zagadnienia
5. Hodowla zwierząt
Aby ocenić wartość hodowlaną ![]() zwierząt na podstawie
zwierząt na podstawie ![]() pomiarów wartości pewnej cechy, stosuje się pewien model liniowy, prowadzący do następującego zagadnienia, opisanego w [29, rozdział 5]:
pomiarów wartości pewnej cechy, stosuje się pewien model liniowy, prowadzący do następującego zagadnienia, opisanego w [29, rozdział 5]:
| (5.1) |
Szukane wartości hodowlane zwierząt oznaczone są jako wektor ![]() (zatem
(zatem ![]() -te zwierzę ma wartość
-te zwierzę ma wartość ![]() ). Niewiadomymi pomocniczymi są parametry wpływu płciowości
). Niewiadomymi pomocniczymi są parametry wpływu płciowości ![]() .
.
Pozostałe parametry występujące w (5.1) — ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() — są zadane jako parametry modelu. Jak to często się zdarza w przypadku obliczeń naukowych, będziemy dysponować jedynie częściową informacją o danych modelu, a naszym zadaniem będzie po prostu wskazanie sensownej metody numerycznego rozwiązywania układu równań liniowych (5.1). Co zatem na początek wiemy o parametrach modelu? Nasz ,,zleceniodawca” z pewnością zwróci nam uwagę na to, że macierze
— są zadane jako parametry modelu. Jak to często się zdarza w przypadku obliczeń naukowych, będziemy dysponować jedynie częściową informacją o danych modelu, a naszym zadaniem będzie po prostu wskazanie sensownej metody numerycznego rozwiązywania układu równań liniowych (5.1). Co zatem na początek wiemy o parametrach modelu? Nasz ,,zleceniodawca” z pewnością zwróci nam uwagę na to, że macierze ![]() oraz
oraz ![]() są macierzami zerojedynkowymi. Macierz
są macierzami zerojedynkowymi. Macierz ![]() rozmiaru
rozmiaru ![]() określa płeć badanego zwierzęcia, a macierz
określa płeć badanego zwierzęcia, a macierz ![]() , rozmiaru
, rozmiaru ![]() , odpowiada za ,,wkład” danego zwierzęcia do badanej cechy hodowlanej.
, odpowiada za ,,wkład” danego zwierzęcia do badanej cechy hodowlanej.
Wreszcie, o macierzy ![]() rozmiaru
rozmiaru ![]() — tzw. macierzy addytywnych pokrewieństw — wiadomo, że ma elementy nieujemne, jest symetryczna i dodatnio określona.
— tzw. macierzy addytywnych pokrewieństw — wiadomo, że ma elementy nieujemne, jest symetryczna i dodatnio określona.
W praktyce [19, Table 1] spotyka się zadania dla ![]() z zakresu od
z zakresu od ![]() do
do ![]() . Macierz addytywnych pokrewieństw
. Macierz addytywnych pokrewieństw ![]() w niektórych modelach może być pominięta (co odpowiada wartości parametru skalującego
w niektórych modelach może być pominięta (co odpowiada wartości parametru skalującego ![]() ), a w ogólności ze względu na swoją naturę powinna ona być dosyć rozrzedzona (hodowcy dążą do tego, by ograniczyć pokrewieństwa pomiędzy osobnikami).
), a w ogólności ze względu na swoją naturę powinna ona być dosyć rozrzedzona (hodowcy dążą do tego, by ograniczyć pokrewieństwa pomiędzy osobnikami).
Poniżej zacytujemy konkretne zadanie modelowe opisane w [29].
Przykład 5.1 (Przykład 62 z [29])
W oparciu o metodę BLUP wykonać ocenę wartości hodowlanej zwierząt dla cechy masa cieląt przy odsadzeniu w oparciu o następujące informacje:
| Cielę | Płeć | Ojciec | Matka | Waga przy odsadzeniu (kg) |
| 4 | buhajek | 1 | - | 4,5 |
| 5 | cieliczka | 3 | 2 | 2,9 |
| 6 | cieliczka | 1 | 2 | 3,9 |
| 7 | buhajek | 4 | 5 | 3,5 |
| 8 | buhajek | 3 | 6 | 5,0 |
Zebrane informacje fenotypowe prowadzą do zadania (5.1), w którym
 |
parametr ![]() , a symetryczna macierz addytywnych pokrewieństw jest zadana przez
, a symetryczna macierz addytywnych pokrewieństw jest zadana przez
 |
5.1. Dyskusja problemu
Zadanie wydaje się łatwe do rozwiązania: dane są macierze i parametry, wskazany jest układ ![]() równań do rozwiązania (5.1) — więc wystarczy zbudować jego macierz i go rozwiązać. Gdy zadanie nie jest zbyt wielkiego rozmiaru (
równań do rozwiązania (5.1) — więc wystarczy zbudować jego macierz i go rozwiązać. Gdy zadanie nie jest zbyt wielkiego rozmiaru (![]() rzędu tysiąca?) — możemy je rozwiązać wprost w Octave. Rzeczywiście, [29, rozdział 10] podaje gotowy skrypt:
rzędu tysiąca?) — możemy je rozwiązać wprost w Octave. Rzeczywiście, [29, rozdział 10] podaje gotowy skrypt:
G = [X'*X, X'*Z ; Z'*X, Z'*Z + k*inv(A)]; r = [X'*y; Z'*y]; s = inv(G)*r; b = s(1:2); a = s(3:end);
Przedyskutujmy wady i zalety powyższego rozwiązania. Tym, co od razu kłuje na w oczy, jest używanie funkcji inv do wyznaczania macierzy odwrotnej do ![]() i do
i do ![]() . O ile macierz odwrotna do
. O ile macierz odwrotna do ![]() występuje w samym sformułowaniu zadania, o tyle wyznaczenie rozwiązania układu równań
występuje w samym sformułowaniu zadania, o tyle wyznaczenie rozwiązania układu równań
metodą s = inv(G)*r powinno zjeżyć nam włos na głowie. Oczywiście, choć matematycznie jest to poprawne, w realizacji numerycznej nie powinniśmy wyznaczać wprost macierzy odwrotnej! Znacznie lepiej dokonać rozkładu LDL macierzy ![]() (wszak jest symetryczna!) i następnie rozwiązać dwa układy równań z macierzami trójkątnymi i jedną diagonalną. Ten algorytm realizuje w Octave operator ,,dzielenia” macierzowego:
(wszak jest symetryczna!) i następnie rozwiązać dwa układy równań z macierzami trójkątnymi i jedną diagonalną. Ten algorytm realizuje w Octave operator ,,dzielenia” macierzowego:
s = G\r;
Zapatrzeni w odwracanie macierzy, możemy przeoczyć inną niepokojącą cechę układu (5.1): jeśli bowiem ![]() , to macierz naszego układu przyjmuje postać:
, to macierz naszego układu przyjmuje postać:
To jest przecież nic innego, jak macierz równań normalnych dla zadania najmniejszych kwadratów
— a zadanie najmniejszych kwadratów, jak wiemy, bezpieczniej rozwiązywać metodami innymi niż poprzez układ równań normalnych: na przykład, opartymi na rozkładzie QR macierzy ![]() . Najpierw jednak musimy zadać sobie pytanie, czy również oryginalny układ (5.1) odpowiada jakiemuś zadaniu najmniejszych kwadratów? Możemy domyślać się, że tak (wiedząc o tym, jaki jest jego rodowód). I rzeczywiście, przecież dla dowolnej macierzy symetrycznej
. Najpierw jednak musimy zadać sobie pytanie, czy również oryginalny układ (5.1) odpowiada jakiemuś zadaniu najmniejszych kwadratów? Możemy domyślać się, że tak (wiedząc o tym, jaki jest jego rodowód). I rzeczywiście, przecież dla dowolnej macierzy symetrycznej ![]() ,
,
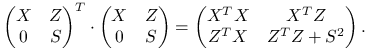 |
Biorąc więc ![]() (istnieje, bo
(istnieje, bo ![]() jest symetryczna i dodatnio określona) dostajemy, że (5.1) jest układem równań normalnych dla zadania najmniejszych kwadratów:
jest symetryczna i dodatnio określona) dostajemy, że (5.1) jest układem równań normalnych dla zadania najmniejszych kwadratów:
| (5.2) |
Problem z ostatnim sformułowaniem problemu polega na tym, że aby go postawić, musimy wyznaczyć ![]() , czyli — w rzeczywistości — rozwiązać pełne zagadnienie własne dla macierzy
, czyli — w rzeczywistości — rozwiązać pełne zagadnienie własne dla macierzy ![]() (znaleźć wszystkie wektory i wartości własne).
(znaleźć wszystkie wektory i wartości własne).
Jednak po chwili namysłu możemy zobaczyć, że ![]() nie musi być symetryczna, wystarczy tylko, żeby
nie musi być symetryczna, wystarczy tylko, żeby ![]() . Biorąc więc (łatwo obliczalny) rozkład Cholesky'ego–Banachiewicza macierzy
. Biorąc więc (łatwo obliczalny) rozkład Cholesky'ego–Banachiewicza macierzy ![]() ,
,
dostajemy ![]() . Ponieważ
. Ponieważ ![]() jest macierzą dolną trójkątną, macierz
jest macierzą dolną trójkątną, macierz ![]() można wyznaczyć przyzwoitym kosztem.
można wyznaczyć przyzwoitym kosztem.
Ostatecznie więc, zamiast zadania (5.1) należy rozwiązać równoważne zadanie najmniejszych kwadratów,
| (5.3) |
Jeśli obecność macierzy odwrotnej w powyższym sformułowaniu wciąż nas niepokoi, możemy drążyć dalej. Rozpisując, dostajemy inną postać minimalizowanego wyrażenia (5.3),
Oznaczając ![]() , mamy równoważnie
, mamy równoważnie
— a tu już nie występuje macierz odwrotna do ![]() ! Ostatecznie, dostajemy następujące sformułowanie zadania wyjściowego (por. [15, zadanie 11.3.4]:
! Ostatecznie, dostajemy następujące sformułowanie zadania wyjściowego (por. [15, zadanie 11.3.4]:
-
Wyznacz rozkład Cholesky'ego
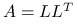 .
. -
Wyznacz rozwiązanie
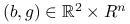 zadania najmniejszych kwadratów
zadania najmniejszych kwadratów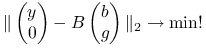
(5.4) gdzie
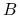 jest prostokątną macierzą rozmiaru
jest prostokątną macierzą rozmiaru 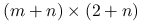 postaci
postaci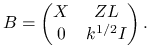
-
Oblicz
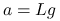 .
.
5.2. Implementacja
Dzięki odpowiedniemu potraktowaniu problemu, całkowicie uniknęliśmy wyznaczania macierzy odwrotnych oraz niepotrzebnego przekształcania zadania najmniejszych kwadratów do postaci normalnej.
Rozkład Cholesky'ego macierzy ![]() wyznaczymy korzystając z funkcji Octave
wyznaczymy korzystając z funkcji Octave
U = chol(A). Jednak musimy pamiętać, że wynikiem działania chol(A) jest macierz trójkątna górna taka, że ![]() , czyli innymi słowy,
, czyli innymi słowy, ![]() . Dlatego musimy odpowiednio dostosować macierz zadania (5.4):
. Dlatego musimy odpowiednio dostosować macierz zadania (5.4):
B = [X Z*U'; zeros(n,2), sqrt(k)*eye(size(U))];
Dalej, wystarczy rozwiązać zadanie najmniejszych kwadratów z macierzą ![]() :
:
f = [y; zeros(n,1)]; q = B \ f; b = q(1:2); a = U'*q(3:end);
Przypomnijmy, że w Octave zadanie najmniejszych kwadratów rozwiązuje się, korzystając z tego samego operatora ,,dzielenia”, \, który służy do rozwiązywania układów równań.
Jednak nasze zadanie jest bardzo szczególnej postaci blokowej: blok ![]() macierzy
macierzy ![]() jest macierzą diagonalną, co może nam pozwolić osiągnąć dalszą redukcję kosztów obliczeń [15, rozdział 11.3]. Ponadto, można od razu tak ponumerować równania, by macierz
jest macierzą diagonalną, co może nam pozwolić osiągnąć dalszą redukcję kosztów obliczeń [15, rozdział 11.3]. Ponadto, można od razu tak ponumerować równania, by macierz ![]() była postaci
była postaci
co spowoduje, że iloczyn ![]() będzie wyznaczalny zerowym kosztem obliczeniowym.
będzie wyznaczalny zerowym kosztem obliczeniowym.
5.3. Wykorzystanie specyfiki zadania
Dotychczas atakowaliśmy postawione zadanie przy minimalnej wiedzy o jego naturze. Staraliśmy się przyjąć neutralny punkt widzenia numeryka, pozwalający nam dostrzec w zadaniu pewne typowe cechy samego zadania obliczeniowego. Jednak tym, co naprawdę jest piękne w obliczeniach naukowych jest to, że zadania — choć na swój sposób typowe — mają swoje niuanse, które powodują, że czasem warto zmienić swój punkt widzenia i dopasować używane metody do tego, co więcej wiemy o charakterze zadania!
Jak dotąd, braliśmy pod uwagę jedynie fakt, że macierz ![]() jest z góry zadana, dosyć rzadka, symetryczna i dodatnio określona. Nie chcieliśmy wyznaczać
jest z góry zadana, dosyć rzadka, symetryczna i dodatnio określona. Nie chcieliśmy wyznaczać ![]() wiedząc, jak niezręcznie jest numerycznie korzystać z takiej macierzy.
wiedząc, jak niezręcznie jest numerycznie korzystać z takiej macierzy.
Przypomnijmy powody:
-
Wyznaczenie macierzy odwrotnej
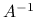 jest procesem bardziej kosztownym niż wyznaczenie współczynników jej rozkładu (np. Cholesky'ego,
jest procesem bardziej kosztownym niż wyznaczenie współczynników jej rozkładu (np. Cholesky'ego, 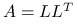 , lub, unikając kosztownych pierwiastków,
, lub, unikając kosztownych pierwiastków, 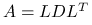 )
) -
Aby dla danego
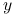 wyznaczyć
wyznaczyć 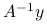 wystarczy rozwiązać dwa układy równań z macierzą
wystarczy rozwiązać dwa układy równań z macierzą 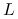 , każdy kosztem co najwyżej
, każdy kosztem co najwyżej 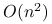 działań (i ewentualnie
działań (i ewentualnie 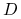 , kosztem liniowym). Tak wyznaczone rozwiązanie numeryczne jest rozwiązaniem pewnego zadania sąsiedniego, o ile tylko użylismy dobrego algorytmu wyznaczania rozkładu macierzy.
, kosztem liniowym). Tak wyznaczone rozwiązanie numeryczne jest rozwiązaniem pewnego zadania sąsiedniego, o ile tylko użylismy dobrego algorytmu wyznaczania rozkładu macierzy. -
Nawet jeśli
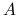 jest macierzą rzadką, to
jest macierzą rzadką, to 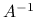 zazwyczaj jest macierzą gęstą.
zazwyczaj jest macierzą gęstą.
Tymczasem okazuje się, że spotykane w praktyce modele (5.1) korzystają z macierzy ![]() , która jest tak zwaną macierzą addytywnych pokrewieństw. Mając zadaną taką macierz, możemy wyznaczyć macierz do niej odwrotną, ale na pierwszy rzut oka nie widać w niej jakiejś wyrazistej regularności:
, która jest tak zwaną macierzą addytywnych pokrewieństw. Mając zadaną taką macierz, możemy wyznaczyć macierz do niej odwrotną, ale na pierwszy rzut oka nie widać w niej jakiejś wyrazistej regularności:
A = [0 0 0 1/2 0 1/2 1/4 1/4; 0 0 0 0 1/2 1/2 1/4 1/4; 0 0 0 0 1/2 0 1/4 1/2; 0 0 0 0 0 1/4 1/2 1/8; 0 0 0 0 0 1/4 1/2 3/8; 0 0 0 0 0 0 1/4 1/2; 0 0 0 0 0 0 0 1/4; 0 0 0 0 0 0 0 0;]; n = size(A,1); A = A + A' + eye(n); inv(A)
Jednak, jeśli sprawdzić w fachowej literaturze (np. w [19]) definicję macierzy ![]() to okaże się, że jej elementy wyznacza się z prostego rekurencyjnego wzoru, który bazuje na znanym z danych hodowlanych rodowodzie każdego zwierzęcia. Spojrzenie na wzór określający
to okaże się, że jej elementy wyznacza się z prostego rekurencyjnego wzoru, który bazuje na znanym z danych hodowlanych rodowodzie każdego zwierzęcia. Spojrzenie na wzór określający ![]() w terminach operacji macierzowych, może słabszych psychicznie zwalić z nóg:
w terminach operacji macierzowych, może słabszych psychicznie zwalić z nóg:
gdzie ![]() jest pewną macierzą o co najwyżej dwóch niezerowych elementach w wierszu! Co więcej, macierz
jest pewną macierzą o co najwyżej dwóch niezerowych elementach w wierszu! Co więcej, macierz ![]() bardzo łatwo wyznaczyć z danych rodowodowych, natomiast
bardzo łatwo wyznaczyć z danych rodowodowych, natomiast ![]() jest zadaną macierzą diagonalną [19]. Stąd oczywiście dostajemy natychmiast bardzo łatwo wyliczalną macierz odwrotną,
jest zadaną macierzą diagonalną [19]. Stąd oczywiście dostajemy natychmiast bardzo łatwo wyliczalną macierz odwrotną,
Widzimy więc, że macierz ![]() nie dość, że jest banalna do wyznaczenia, to od razu jest dana w postaci rozkładu
nie dość, że jest banalna do wyznaczenia, to od razu jest dana w postaci rozkładu ![]() , w którym co prawda
, w którym co prawda ![]() nie musi być trójkątna górna, ale za to na pewno jest bardzo rozrzedzona (ma tylko około
nie musi być trójkątna górna, ale za to na pewno jest bardzo rozrzedzona (ma tylko około ![]() niezerowych elementów.
niezerowych elementów.
To odkrycie zmienia nasz punkt widzenia! Jeśli bowiem mamy do dyspozycji rozrzedzoną macierz ![]() i diagonalę
i diagonalę ![]() macierzy
macierzy ![]() , konstrukcja macierzy zadania najmniejszych kwadratów (5.2) upraszcza się do utworzenia bloku
, konstrukcja macierzy zadania najmniejszych kwadratów (5.2) upraszcza się do utworzenia bloku ![]() , co możemy zaimplementować w Octave na przykład w poniższy sposób:
, co możemy zaimplementować w Octave na przykład w poniższy sposób:
B = [X Z; zeros(n,2), spdiag(sqrt(k*d))*(speye(n)-P)];
5.4. Przypadek dużego 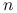
Niektóre badania mogą dotyczyć ![]() zwierząt (
zwierząt (![]() , czyli zbiór danych pomiarowych) jest wtedy zwykle dużo mniejsze), więc każdy sposób na to, by obniżyć koszt pamięciowy i obliczeniowy wyznaczenia rozwiązania jest wart uwagi.
, czyli zbiór danych pomiarowych) jest wtedy zwykle dużo mniejsze), więc każdy sposób na to, by obniżyć koszt pamięciowy i obliczeniowy wyznaczenia rozwiązania jest wart uwagi.
Macierze rzadkie
Przede wszystkim, należy wykorzystać fakt, że macierze ![]() są w praktyce macierzami mocno rozrzedzonymi.
są w praktyce macierzami mocno rozrzedzonymi.
Jeśli więc utworzymy ![]() jako macierze rzadkie (poleceniem
jako macierze rzadkie (poleceniem sparse), to macierz ![]() też będzie rzadka. W przypadku, gdy operator
też będzie rzadka. W przypadku, gdy operator \ zostanie przyłożony do prostokątnej macierzy rzadkiej, spowoduje wywołanie specjalizowanej funkcji bibliotecznej z pakietu CXSPARSE, wykonującej rzadki rozkład QR.
Zmniejszenie rozmiaru zadania przez powrót do układu równań normalnych
Równań normalnych nie musimy się obawiać, gdy uwarunkowanie macierzy ![]() jest nieduże. W niektórych przypadkach tak rzeczywiście będzie nawet dla bardzo dużych
jest nieduże. W niektórych przypadkach tak rzeczywiście będzie nawet dla bardzo dużych ![]() . Należy jednak pamiętać, że jeśli
. Należy jednak pamiętać, że jeśli ![]() , to zastąpienie macierzy prostokątnej
, to zastąpienie macierzy prostokątnej ![]() rozmiaru
rozmiaru ![]() macierzą kwadratową
macierzą kwadratową ![]() rozmiaru
rozmiaru ![]() nie musi dawać znaczących zysków, zwłaszcza, że
nie musi dawać znaczących zysków, zwłaszcza, że ![]() będzie mniej rozrzedzona niż
będzie mniej rozrzedzona niż ![]() .
.
Użycie metody iteracyjnej
Gdy ![]() jest na tyle duże, że układ równań normalnych
jest na tyle duże, że układ równań normalnych ![]() stanowiłby poważne wyzwanie dla metody bezpośredniej, można byłoby wówczas skorzystać z metody iteracyjnej rozwiązywania układu
stanowiłby poważne wyzwanie dla metody bezpośredniej, można byłoby wówczas skorzystać z metody iteracyjnej rozwiązywania układu ![]() — na przykład, moglibyśmy tu zastosować metodę PCG, jednak wyłącznie wówczas, gdy wyjściowe zadanie jest bardzo dobrze uwarunkowane.
— na przykład, moglibyśmy tu zastosować metodę PCG, jednak wyłącznie wówczas, gdy wyjściowe zadanie jest bardzo dobrze uwarunkowane.
Stosując metodę iteracyjną, można przy okazji uniknąć składania całej wielkiej macierzy ![]() : wystarczy, zgodnie z powyższym przepisem, przyłożyć macierz do wektora, co możemy zapisać stosunkowo prostą funkcją.
: wystarczy, zgodnie z powyższym przepisem, przyłożyć macierz do wektora, co możemy zapisać stosunkowo prostą funkcją.
Alternatywą dla rozwiązania układu równań normalnych metodą PCG możne być rozwiązanie (nieco lepiej uwarunkowanego) zadania z (pozornie!) wielką macierzą kwadratową ![]() rozmiaru
rozmiaru ![]() , o bardzo specjalnej, prostej strukturze:
, o bardzo specjalnej, prostej strukturze:
gdzie ![]() jest zadanym parametrem dobranym do zadania.
jest zadanym parametrem dobranym do zadania.
Rzeczywiście, ![]() jest rozwiązaniem powyższego równania wtedy i tylko wtedy, gdy
jest rozwiązaniem powyższego równania wtedy i tylko wtedy, gdy ![]() jest rozwiązaniem zadania najmniejszych kwadratów
jest rozwiązaniem zadania najmniejszych kwadratów ![]() , a
, a ![]() jest przeskalowanym wektorem residuum.
jest przeskalowanym wektorem residuum.
Ponieważ macierz ![]() jest symetryczna, ale nie jest dodatnio określona, należy zastosować do niej metodę PCR, dostępną m.in. w Octave. Prostoduszna implementacja
jest symetryczna, ale nie jest dodatnio określona, należy zastosować do niej metodę PCR, dostępną m.in. w Octave. Prostoduszna implementacja
M = [alpha*speye(size(B,1)), B; B', spalloc(size(B,2),size(B,2))]; [X,info,relres] = pcr(M,[y;zeros(size(B,2),1)]); info q = X(size(B,1)+1:end);może efektywnością ustąpić miejsca bardziej wyrafinowanej, korzystającej z operatorowej definicji
Mmult = @(x) [alpha*x(1:size(B,1)) + B*x(size(B,1)+1:end); B'*x(1:size(B,1))]; [X,info,relres] = pcr(Mmult,[y;zeros(size(B,2),1)]); info q = X(size(B,1)+1:end);Koszt mnożenia wektora przez
Obniżenie kosztu mnożenia przez 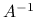
Możemy też próbować mnożenie przez ![]() uczynić tańszym, zwłaszcza, gdy implementujemy nasz program w języku C lub podobnym. Z pomocą przychodzi tu doświadczenie… programowania metody elementu skończonego (technika stosowana w numerycznych obliczeniach inżynierskich!). Ponieważ w wierszu
uczynić tańszym, zwłaszcza, gdy implementujemy nasz program w języku C lub podobnym. Z pomocą przychodzi tu doświadczenie… programowania metody elementu skończonego (technika stosowana w numerycznych obliczeniach inżynierskich!). Ponieważ w wierszu ![]() odpowiadającym
odpowiadającym ![]() -temu zwierzęciu znajdują się co najwyżej dwie niezerowe wartości:
-temu zwierzęciu znajdują się co najwyżej dwie niezerowe wartości:
gdy ojcem ![]() jest zwierzę o numerze
jest zwierzę o numerze ![]() , a matką — zwierzę o numerze
, a matką — zwierzę o numerze ![]() , a w przypadku, gdy znane jest tylko jedno z rodziców,
, a w przypadku, gdy znane jest tylko jedno z rodziców, ![]() , tylko jeden element jest niezerowy,
, tylko jeden element jest niezerowy,
a gdy żadne z rodziców zwierzęcia ![]() nie jest znane, cały
nie jest znane, cały ![]() -ty wiersz
-ty wiersz ![]() jest zerowy, natomiast
jest zerowy, natomiast ![]() .
.
Stąd wynika, że ![]() , gdzie
, gdzie ![]() jest wkładem
jest wkładem ![]() -tego zwierzęcia. Na przykład, gdy znani są oboje rodzice zwierzęcia,
-tego zwierzęcia. Na przykład, gdy znani są oboje rodzice zwierzęcia,
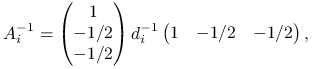 |
przy czym elementy tej macierzy należy rozrzucić na trójkę ![]() współrzędnych
współrzędnych ![]() .
.
Ćwiczenie 5.1
Niech będzie dana tabela ![]() , rozmiaru
, rozmiaru ![]() , określająca bezpośrednie relacje pomiędzy zwierzętami:
, określająca bezpośrednie relacje pomiędzy zwierzętami:
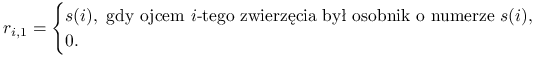 |
Podobnie określamy ![]() , identyfikator matki zwierzęcia
, identyfikator matki zwierzęcia ![]() . Niech
. Niech ![]() rozmiaru
rozmiaru ![]() będzie macierzą addytywnych pokrewieństw pomiędzy zwierzętami wyznaczoną przez
będzie macierzą addytywnych pokrewieństw pomiędzy zwierzętami wyznaczoną przez ![]() . Napisz możliwie szybko działającą procedurę, obliczającą
. Napisz możliwie szybko działającą procedurę, obliczającą ![]() na zadanym wektorze
na zadanym wektorze ![]() przy minimalnym zapotrzebowaniu na pamięć roboczą.
przy minimalnym zapotrzebowaniu na pamięć roboczą.
Jeśli chcesz zbliżyć się do realnych warunków pracy, przyjmij założenie, że dane z tablicy ![]() są zapisane w arkuszu kalkulacyjnym Excela (lub w jakimś bardziej egzotycznym formacie): konwersja formatów danych to jeden z pomijanych, a bardzo uciążliwych programistycznie, aspektów obliczeń naukowych.
są zapisane w arkuszu kalkulacyjnym Excela (lub w jakimś bardziej egzotycznym formacie): konwersja formatów danych to jeden z pomijanych, a bardzo uciążliwych programistycznie, aspektów obliczeń naukowych.
Ćwiczenie 5.2
W bardzo licznych zastosowaniach statystycznych należy wskazać zestaw tych wartości własnych (i, przy okazji, wektorów własnych) macierzy kowariancji ![]() , które są powyżej zadanego progu
, które są powyżej zadanego progu ![]() . To zadanie nazywa się analizą głównych składowych (principal component analysis, PCA), a celem może być zmniejszenie rozmiaru zbioru danych statystycznych poprzez eliminację mało istotnych parametrów.
. To zadanie nazywa się analizą głównych składowych (principal component analysis, PCA), a celem może być zmniejszenie rozmiaru zbioru danych statystycznych poprzez eliminację mało istotnych parametrów.
W sformułowaniu matematycznym, mając zadaną macierz ![]() — przy czym
— przy czym ![]() — musimy wyznaczyć rozkład spektralny macierzy (symetrycznej i nieujemnie określonej)
— musimy wyznaczyć rozkład spektralny macierzy (symetrycznej i nieujemnie określonej) ![]() :
:
gdzie ![]() jest macierzą diagonalną, zawierającą wartości własne, a
jest macierzą diagonalną, zawierającą wartości własne, a ![]() jest macierzą ortogonalną,
jest macierzą ortogonalną, ![]() , złożoną z wektorów własnych macierzy
, złożoną z wektorów własnych macierzy ![]() , a następnie zwrócić te wektory własne
, a następnie zwrócić te wektory własne ![]() , które spełniają warunek
, które spełniają warunek ![]() .
.
Napisz funkcję, która wykona to zadanie.
Funkcja Octave, realizująca nasze zadanie mogłaby mieć postać:
function [V, L] = pca1(X, eta) [V, L] = eig(X'*X); [L, I] = sort(diag(L), 'descend'); V = V(:,I); I = find(L>eta); V = V(:,I); L = L(I); end
Dodatkowo, nasza funkcja sortuje wektory i wartości własne w kolejności od największej, do najmniejszej.
Jednak ma ona tę wadę, że formując macierz ![]() tracimy informację zawartą w
tracimy informację zawartą w ![]() : macierz
: macierz ![]() jest wymiaru tylko
jest wymiaru tylko ![]() . Dlatego bezpieczniej skorzystać z rozkładu SVD13Więcej o rozkładzie według wartości szczególnych (SVD) dowiesz się z wykładu z Matematyki Obliczeniowej II. macierzy
. Dlatego bezpieczniej skorzystać z rozkładu SVD13Więcej o rozkładzie według wartości szczególnych (SVD) dowiesz się z wykładu z Matematyki Obliczeniowej II. macierzy ![]() :
:
i faktu, że ![]() . Ponieważ funkcja
. Ponieważ funkcja svd zwraca macierze ![]() , lepsza numerycznie wersja naszej funkcji miałaby następującą postać:
, lepsza numerycznie wersja naszej funkcji miałaby następującą postać:
function [V, L] = pca(X, eta) [U L V] = svd(X,0); % economy-version [L, I] = sort(diag(L).^2, 'descend'); V = V(:,I); I = find(L>eta); V = V(:,I); L = L(I); end




